一种基于数据驱动的多信任度协同元模型在预测燃料舱焊接变形的应用方法

1.本发明属于焊接技术领域，尤其涉及一种基于数据驱动的多信任度协同元模型在预测燃料舱焊接变形的应用方法。


背景技术：

2.在现代先进的突防装备中，为了能够使产品满足射程、精度、突防等指标，某型号的产品具有外形复杂、高精密度、外形复杂等显著特点，其关键构件的加工涉及焊接等热加工工艺。由于试验费用大，研制周期长等特点，一直存在试验样本少、工况参数依靠有经验的工人进行经验试错等问题。在生产制造过程中，实际制造之前采用数字化设计对制造过程进行有限元仿真分析，但是由于一些大型的复杂构件在数字化仿真环节，需要耗费大量的时间，几天几周甚至几个月。而且随着产品性能要求的提升，会导致产品工艺的快速迭代更新，从而生产制造过程呈现出小批量、多品种、离散度高、研制周期短和费用昂贵等特点，加上对工件的尺寸严格要求，其工艺设计的质量和效率直接影响生产质量。目前大多生产线仍然是靠传统的工艺设计流程，依靠有经验的一线人员来不断试错改进，试验生产周期长达一两个月。所以，为了缩短研发的周期以满足企业制造的快速响应能力，焊接变形预测能力亟待提升。
3.引入元模型到数字化仿真设计与制造是智能制造过程关键的一步，所谓元模型，就是利用一些近似数学模型去替代那些在仿真过程中比较复杂和费时的数值分析。元模型能够大幅度提高设计效率，简化仿真流程，并且能够实现自适应元模型的构建。元模型根据样本点的获取方式，分为自适应元模型和非自适应元模型。非自适应是通过前期的样本点集直接构建元模型，构建好的元模型不会再变化更新；而自适应元模型则是根据加点准则，来更新需要增加的样本点，对元模型进行重新构建，重复迭代优化直接满足收敛准则。自适应元模型在处理实际工程问题时，能够同时保持高效性、鲁棒性、自适应性的优点。
4.在工程研究的领域中，元模型多用于结构优化、气动优化、飞行器设计优化、多目标优化等。把自适应元模型运用到焊接热变形问题求解中，可为设计方和制造厂商节约大量时间和成本，进一步为工件的研发和设计提供参考，具有直接的工程实用价值。


技术实现要素：

5.针对上述技术问题，本发明提供了一种基于数据驱动的多信任度协同元模型在预测燃料舱焊接变形的应用方法，旨在用数学模型替代昂贵、耗时的有限元仿真，进而达到预测焊接热变形量的目的。
6.1.本发明的及技术方案是：一种基于数据驱动的多信任度协同元模型在预测燃料舱焊接变形的应用方法，其特征在于，包括以下步骤：
7.a、建立工件的多信任度有限元分析模型以及区间多信任度样本点的选取；
8.b、以有限元仿真模型变形量最大值作为响应值，根据初始样本点的信息以及响应
值，构建初始协同元模型；
9.c、对步骤b中建立的协同元模型进行精度验证，如满足要求则进行步骤d，如不满足要求，则利用加点准则对协同元模型进行优化迭代，直到满足精度要求；
10.d、根据最终迭代完成的协同元模型，对焊接工件的变形进行预测；
11.2.如权力要求1所述的方法，其特征在于，在所述步骤a中，建立工件的多信任度有限元分析模型以及区间多信任度样本点的选取具体步骤为：
12.a1、建立焊接工件的三维结构模型；
13.a2、在有限元仿真分析软件中，对焊接工件模型的材料属性进行参数设置，材料的属性包括材料的密度、热膨胀系数、杨氏模量、泊松率、屈服强度、热导系数和比热等。
14.a3、对焊接工件模型进行多信任度的网格划分，即划分网格粗糙为高信任度，划分网格细致为低信任度，并设置初始条件、边界条件和分析设置，具体网格划分类型根据焊接工件的结构，选择适应的四面体网格或者六面体网格；初始条件与边界条件包括初始环境温度、热对流换热系数和约束受力条件等；
15.a4、确定热源模型以及热源参数变量，根据具体的加工设备以及工况进行确定，热源包括电子束和激光，而热源模型包括高斯热源模型、双椭球热源模型和半球状热源模型等，其中热源参数包括但不限于焊接电压、焊接电流、激光功率、热源移动速度等；
16.a5、对热源参数变量利用最优拉丁超立方抽样算法进行初始样本点的选取，选取两组样本点分别作为高信任度和低信任度的样本信息，根据确定的热源参数变量来确定对应热源参数的变化区间，采用最优拉丁超立方抽样算法进行区间抽样，其抽样点在每个坐标轴的投影都具有均匀性；
17.3.如权力要求1所述的方法，其特征在于，在所述步骤b中，根据有限元仿真模型变形量最大值作为响应值，以热源参数作为协同元模型的输入参数x，响应值作为协同元模型的输出参数y，建立协同元模型的具体步骤为：
18.b1、高信任度模型的n个样本点为xh＝[x
h(1)
,x
h(2)
,...,x
h(n)
]
t
，对应的响应值为yh＝[y
h(1)
,y
h(2)
,...,y
h(n)
]
t
，假设将yh视为一个稳态随机过程，所以yh替换为如下随机过程的实现，即yh＝βh+zh(x)，则将以此建立高信任度模型；
[0019]
b2、低信任度模型的n个样本点为x
l
＝[x
l(1)
,x
l(2)
,...,x
l(n)
]
t
，对应的响应值为y
l
＝[y
l(1)
,y
l(2)
,...,y
l(n)
]
t
，假设将y
l
视为一个稳态随机过程，所以y
l
替换为如下随机过程的实现，即y
l
＝β
l
+z
l
(x)，则将以此建立低信任度模型；
[0020]
b3、将高信任度元模型和低信任度元模型耦合在一起组成协同元模型，其中，λh、λ
l
为权重系数，且λh+λ
l
＝1；
[0021]
4.如权力要求1所述的方法，其特征在于，在所述步骤c中，利用在步骤b3中建立的协同元模型，对随机抽取的验证集进行预测，其预测结果为y
pre
，真实响应为y
real
，模型的精度判定准则为决定系数r2，其公式为：
[0022][0023]
式中，ss
regression
是模型的预测值y
pre
与真实响应y
real
的误差平方和，ss
total
是所有样本点平均值y
mean
与真实响应y
real
之间误差的平方和，r2变化区间为[0,1]，数值越接近1，模型预测越准确可靠，通常认为r2大于0.8即模型预测准确可靠，模型满足精度要求，终止
迭代；若r2小于0.8，则利用mei(maximizing expected improvement，最大改善期望)自适应加点准则，进行高信任度更新样本点的选取；在协同元模型中，设当前样本点集中最优点的响应值为y
min
，对于任意一个热源输入参数x，其预测的响应值也就是输出参数服从均值为标准差为的正态分布随机变量，即其概率密度为：
[0024][0025]
定义该x点的目标函数改善i(x)为：
[0026][0027]
对上式求期望得到改善期望函数e[i(x)]：
[0028][0029]
式中，φ(
·
)是标准正态概率密度函数，由分析可得增大和减小时，使e[i(x)]增大，分别进行全局探索和局部探索添加样本点，直到r2大于0.8，终止迭代。
[0030]
5.如权力要求1所述的方法，其特征在于，在所述步骤d中，对完成迭代的协同元模型输入热源参数，能够输出对应的有限元仿真模型变形量预测值。
[0031]
本发明的有益效果是：本发明提出一种基于数据驱动的多信任度协同元模型在预测燃料舱焊接变形的应用方法。在燃料舱焊接变形预测案例中，首次将自适应加点准则以及协同元模型应用在焊接领域，解决高耗时、高成本的焊接变形预测问题，适应企业生产制造过程中小批量、多品种、离散度高、研制周期短的特点，并降低成本以满足企业制造的快速响应能力，具有直接的工程实用价值。
附图说明
[0032]
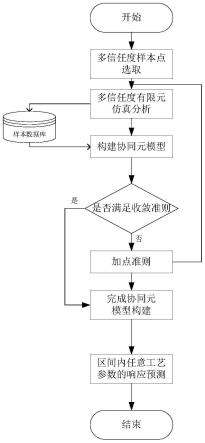
图1是本发明中的一种基于数据驱动的多信任度协同元模型在预测燃料舱焊接变形的应用方法流程示意图。
[0033]
图2是本发明中的燃料舱结构示意图。
具体实施方式
[0034]
为了使本发明的目的以及技术方案更加清晰，下面结合具体案例进行详细地说明。应当理解此处所描述的具体实施案例仅用于解释本发明，但不限定于本发明。
[0035]
如图1所示，为本发明一种基于数据驱动的多信任度协同元模型在预测燃料舱焊接变形的应用方法示意流程图。一种基于数据驱动的多信任度协同元模型在预测燃料舱焊接变形的应用方法，包括以下步骤：
[0036]
a、建立工件的多信任度有限元分析模型以及区间多信任度样本点的选取；
[0037]
b、以有限元仿真模型变形量最大值作为响应值，根据初始样本点的信息以及响应值，构建初始协同元模型；
[0038]
c、对步骤b中建立的协同元模型进行精度验证，如满足要求则进行步骤d，如不满
足要求，则利用加点准则对协同元模型进行优化迭代，直到满足精度要求；
[0039]
d、根据最终迭代完成的协同元模型，对焊接工件的变形进行预测；
[0040]
所述步骤a中建立工件的多信任度有限元分析模型以及区间多信任度样本点的选取具体步骤为：
[0041]
a1、本发明以燃料舱的焊接为例。利用ansys根据相关参数进行几何模型的建立。其中，包括三维尺寸，整体长1548mm、半径332-354mm、最小半径弧度261.72
°
[0042]
a2、对焊接工件的材料属性的具体设置为：设置材料为5a06，密度如表1所示、热膨胀系数为2.3e-5c-1
、杨氏模量为7.1e10 pa、泊松率为0.33、屈服强度为1.45e8 pa、热导系数如表2所示、比热如表3所示。
[0043]
表1密度表
[0044]
温度(c)20100150200250300350400密度(kg
·
m-3
)26402620261026002590258025602550
[0045]
表2热导系数表
[0046]
温度(c)20100150200250300350400热导系数(w
·
m-1
·
c-1
)110.6121.9127.8132.8138.2140.9144.3147.2
[0047]
表3比热表
[0048]
温度(c)20100150200250300350400比热(w
·
m-1
·
c-1
)903.8946.3969.6991.41012.41033.41054.61081.7
[0049]
a3、确定网格划分类型为六面体单元划分，高可信度网格大小为2mm，低可信度网格大小为4mm；初始条件设置环境初始温度为22℃，热对流换热系数为80w/m2·
℃，约束为bonded类型。
[0050]
a4、确定热源为激光，选择热源模型为双椭球热源模型，根据设定确定不同的激光功率以及焊接速度，根据经验，确定焊接功率的区间为2kw-4kw，焊接速度的区间为0.01m/s-0.04m/s，
[0051]
a5、采用最优拉丁超立方抽样算法分别对高信任度和低信任度进行区间随机抽样10个点作为样本点，其抽样点在每个坐标轴的投影都具有均匀性，即抽样点在焊接功率区间与焊接速度区间在对应坐标轴的投影都具有均匀性。
[0052]
所述步骤b中，根据有限元仿真模型变形量最大值作为响应值，以热源参数作为协同元模型的输入参数x，响应值作为协同元模型的输出参数y，建立协同元模型的具体步骤为：
[0053]
b1、高信任度模型的10个样本点为xh＝[x
h(1)
,x
h(2)
,...,x
h(10)
]
t
，对应的响应值为yh＝[y
h(1)
,y
h(2)
,...,y
h(10)
]
t
，假设将yh视为一个稳态随机过程，所以yh替换为如下随机过程的实现，即yh＝βh+zh(x)，则将以此建立高信任度模型；
[0054]
b2、低信任度模型的10个样本点为x
l
＝[x
l(1)
,x
l(2)
,...,x
l(10)
]
t
，对应的响应值为y
l
＝[y
l(1)
,y
l(2)
,...,y
l(10)
]
t
，假设将y
l
视为一个稳态随机过程，所以y
l
替换为如下随机过程的实现，即y
l
＝β
l
+z
l
(x)，则将以此建立低信任度模型；
[0055]
b3、将高信任度元模型和低信任度元模型耦合在一起组成协同元模型，b3、将高信任度元模型和低信任度元模型耦合在一起组成协同元模型，其中，λh、λ
l
为权重系数，且λh+λ
l
＝1；
[0056]
所述步骤c中，利用在步骤b中建立的协同元模型，对随机抽取的验证集进行预测，其预测结果为y
pre
，真实响应为y
real
，模型的精度判定准则为决定系数r2，其公式为：
[0057][0058]
式中，ss
regression
是模型的预测值y
pre
与真实响应y
real
的误差平方和，ss
total
是所有样本点平均值y
mean
与真实响应y
real
之间误差的平方和，r2变化区间为[0,1]，数值越接近1，模型预测越准确可靠，通常认为r2大于0.8即模型预测准确可靠，模型满足精度要求，终止迭代；若r2小于0.8，则利用mei(maximizing expected improvement，最大改善期望)自适应加点准则，进行高信任度更新样本点的选取；在协同元模型中，设当前样本点集中最优点的响应值为y
min
，对于任意一个热源输入参数x，其预测的响应值也就是输出参数服从均值为标准差为的正态分布随机变量，即其概率密度为：
[0059][0060]
定义该x点的目标函数改善i(x)为：
[0061][0062]
对上式求期望得到改善期望函数e[i(x)]：
[0063][0064]
式中，φ(
·
)是标准正态概率密度函数。由分析可得增大和减小时，使e[i(x)]增大，分别进行全局探索和局部探索添加样本点，直到r2大于0.8，终止迭代。
[0065]
所述步骤d中，对完成迭代的协同元模型输入热源参数，能够输出对应的有限元仿真模型变形量预测值。
[0066]
本领域的普通技术人员将会意识到，这里所述的实施例是为了帮助读者理解本发明的原理，应被理解为本发明的保护范围并不局限于这样的特别陈述和实施例。本领域的普通技术人员可以根据本发明公开的这些技术启示做出各种不脱离本发明实质的其它各种具体变形和组合，这些变形和组合仍然在本发明的保护范围内。