静电驱动微执行器吸合电压的计算方法、系统及存储介质

1.本发明属于mems执行器技术领域，尤其涉及一种静电驱动微执行器吸合电压的计算方法、系统及存储介质。


背景技术：

2.目前，mems执行器具有体积小、功耗低、响应快和易于电路集成等特点，可以广泛应用于通讯、宇航、自动化仪器和汽车等领域，能够大大降低系统成本，提高工作效率。吸合电压是静电型mems微执行器的主要技术指标之一，低吸合电压不仅可以降低器件对外部驱动电路的要求，拓展其应用场合,而且可以提高其可靠性。在面积一定的情况下，吸合电压受悬臂梁刚度和极板间隙的影响，刚度过低或间隙过小不仅抗冲击性能差，环境温度适应低，而且容易发生微焊接失效，而刚度过高或间隙过大又会带来吸合电压高，结构响应慢和工作寿命短等问题。吸合电压已成为制约许多mems器件在诸多领域如航空航天中商品化应用的关键问题，受到广泛关注，因此吸合电压的计算及其受各因素影响的规律是微执行器的重要研究方向之一。
3.通过上述分析，现有技术存在的问题及缺陷为：在面积一定的情况下，吸合电压受悬臂梁刚度和极板间隙的影响，刚度过低或间隙过小不仅抗冲击性能差，环境温度适应低，而且容易发生微焊接失效，而刚度过高或间隙过大又会带来吸合电压高，结构响应慢和工作寿命短等问题。


技术实现要素：

4.针对现有技术存在的问题，本发明提供了一种静电驱动微执行器吸合电压的计算方法、系统及存储介质。
5.本发明是这样实现的，一种静电驱动微执行器吸合电压的计算方法包括：基于静电场和弹性薄板理论，对微机电系统mems中的静电型悬臂梁式执行器的吸合现象进行理论分析；借助有限元软件comsol完成吸合电压的计算并与实际测试结果进行对比，验证计算模型的可行性；在悬臂梁面积不变的情况下，利用所述模型分析悬臂梁厚度和极板间隙对吸合电压的影响。
6.进一步，所述静电驱动微执行器吸合电压的计算方法包括以下步骤：步骤一，对吸合电压进行理论分析，得电容器存储能量与电容极板距离之间的关系、极板之间的静电吸引力、平衡位置和吸合电压的关系；步骤二，借助有限元软件comsol建立吸合电压的仿真模型，并对仿真值和实测值进行对比，误差控制在10%以内，验证仿真模型的可行性；步骤三，利用所述模型分析悬臂梁厚度和极板间隙对吸合电压的影响规律。
7.进一步，所述步骤一中的对吸合电压进行理论分析包括：静电型微执行器由可动电极、固定电极和信号电源组成；所述可动电极和固定电极之间形成平行板电容，当极板间未施加电压时，所述可动电极处于初始位置，执行器处于
断开状态；当极板间施加电压时，电容极板进行电荷累积，极板间形成电场，所述可动电极在静电力作用下有向下运动的趋势，当静电力达到一定程度时，所述可动电极向下弯曲并与信号源发生接触，此时信号电源左右导通，执行器处于导通状态。
8.电容器存储的能量为：(1)式中，电容c为： (2)式中，a为两极板交叠面积，ε是真空介电常数，d是极板间初始间隙。
9.根据式(1)、式(2)，得电容器存储能量与电容极板距离之间的关系为： (3)对式(3)的d求一阶偏导，得到极板之间的静电吸引力fe为： (4)在静电吸合过程中，假设电压缓慢变化即不考虑极板的震荡，同时忽略惯性阻尼等因素的影响，可动电极受静电力有向下运动的趋势，则悬臂梁会产生弹性力来与静电力平衡，当极板间隙减小x，此时系统达到平衡，则：
ꢀꢀ
(5)将式(5)整理成关于x的函数： (6)当系统处于平衡时，做功为零，对式(6)两端分别对x求导得：
ꢀꢀ
(7)最终的平衡位置和吸合电压为： (8) (9)由式(9)可知，可动极板向下运动至间隙1/3处，为静电力和机械回复力平衡的临界位置，如果静电力仍持续增大，两极板将迅速吸合直到接触到一起。
10.进一步，所述步骤二中的仿真模型的建立包括：针对mems继电器建立仿真模型，器件主体结构采用单端固定式悬臂梁，所述悬臂
梁由镂空的悬簧、静电驱动极板和触点构成，所述镂空的悬簧使悬臂梁的刚度在合理区间内，为mems继电器提供合适的回复力，以保证较低的驱动电压、较高的稳定度以及较小的开断延时。
11.针对mems继电器建立有限元模型，采用固体力学+静电模块模拟静电吸合作用，整体网格采用六面体，由于悬臂梁在厚度方向发生变形，故厚度方向上网格应保证在3层以上，端部采用固定约束，并对网格进行粗化处理。
12.对极板电压参数化求解，获得悬臂梁在不同电压下的应力和位移分布，悬臂梁根部应力集中，当极板位移超过平衡位置时，两极板会发生迅速吸合，此时极板位移梯度较大，出现明显拐点。
13.进一步，所述步骤二中的仿真模型的验证包括：通过对实际产品进行测试验证仿真模型的准确性，测试设备采用手动探针台和半导体分析仪，测试方法使用2路探针分别接触继电器驱动电极与输入端，另外2路探针接地，分别连接半导体分析仪的smm1、smm2及接地端，施加电压，使输入电压从0开始增加至继电器动作，测量规定的工作电压值，并对多组产品进行测量并与仿真值进行对比，验证计算吸合电压的仿真模型的可行性。
14.进一步，所述步骤三中的利用所述模型分析悬臂梁厚度和极板间隙对吸合电压的影响规律包括：在面积一定的情况下，吸合电压受悬臂梁刚度和极板间隙的影响；借助已经验证的吸合电压仿真模型进行，对影响因素采用控制变量法即其他参数保持不变只改变单一因素的量值，观察吸合电压的变化量。由于悬臂梁刚度受厚度影响，故分析吸合电压随悬臂梁厚度的变化规律。
15.本发明的另一目的在于提供一种应用所述的静电驱动微执行器吸合电压的计算方法的静电驱动微执行器吸合电压的计算系统，所述静电驱动微执行器吸合电压的计算系统包括：吸合电压分析模块，用于对吸合电压进行理论分析；仿真模型构建模块，用于借助有限元软件comsol建立吸合电压仿真模型；仿真模型验证模块，用于对仿真值和实测值进行对比，误差控制在10%以内，验证所述仿真模型的可行性；模型分析模块，用于利用所述仿真模型分析悬臂梁厚度和极板间隙对吸合电压的影响规律。
16.本发明的另一目的在于提供一种计算机可读存储介质，存储有计算机程序，所述计算机程序被处理器执行时，使得所述处理器执行如下步骤：基于静电场和弹性薄板理论，对微机电系统mems中的静电型悬臂梁式执行器的吸合现象进行理论分析；借助有限元软件comsol完成吸合电压的计算并与实际测试结果进行对比，验证计算模型的可行性；在悬臂梁面积不变的情况下，利用所述模型分析悬臂梁厚度和极板间隙对吸合电压的影响。
17.结合上述的所有技术方案，本发明所具备的优点及积极效果为：本发明提供的静电驱动微执行器吸合电压的计算方法，基于静电场和弹性薄板理论，对微机电系统（mems）中常见的静电型悬臂梁式执行器的吸合现象进行了理论分析。本发明借助有限元软件
comsol完成了吸合电压的计算并与实际测试结果进行了对比，误差控制在10%以内，验证了该计算模型的可行性。在悬臂梁面积不变的情况下，本发明利用该模型研究了悬臂梁厚度和极板间隙对吸合电压的影响，结果表明厚度和间隙对吸合电压的影响呈非线性规律，可以对后续执行器的设计提供理论依据。
18.本发明对静电驱动微执行器的吸合电压进行了理论推导，借助comsol有限元软件建立了吸合电压的仿真模型，并与实际测试进行了对比，误差控制在10%以内，因此建立的仿真模型是可行的。利用仿真模型研究了悬臂梁厚度和极板间隙对吸合电压的影响规律，吸合电压随影响因素的增大呈非线性增长，利用多项式可对变化规律进行拟合，为后续执行器在各种使用环境下的优化提供理论依据。
附图说明
19.为了更清楚地说明本发明实施例的技术方案，下面将对本发明实施例中所需要使用的附图做简单的介绍，显而易见地，下面所描述的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下还可以根据这些附图获得其他的附图。
20.图1是本发明实施例提供的静电驱动微执行器吸合电压的计算方法流程图；图2是本发明实施例提供的静电驱动微执行器吸合电压的计算系统结构图；图3是本发明实施例提供的静电型微执行器原理图；图4是本发明实施例提供的mems继电器结构示意图；图5是本发明实施例提供的mems继电器网格示意图；图6是本发明实施例提供的继电器等效应力分布云图；图7是本发明实施例提供的吸合电压与悬臂梁端点位移的对应关系示意图；图8是本发明实施例提供的继电器加工结构示意图；图9是本发明实施例提供的继电器测试结果示意图；图中（a）为继电器测试中吸合电压与工作电压的图形、图像一；图中（b）为继电器测试中，吸合电压与工作电压的图形、图像二；图10是本发明实施例提供的吸合电压测试值与仿真值对比示意图；图11是本发明实施例提供的不同悬臂梁厚度下的吸合电压分布示意图；图12是本发明实施例提供的不同极板间隙下的吸合电压分布示意图；图中：1、吸合电压分析模块；2、仿真模型构建模块；3、仿真模型验证模块；4、模型分析模块；5、可动电极；6、固定电极；7、信号电源；8、镂空的悬簧；9、静电驱动极板；10、触点。
具体实施方式
21.为了使本发明的目的、技术方案及优点更加清楚明白，以下结合实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。
22.针对现有技术存在的问题，本发明提供了一种静电驱动微执行器吸合电压的计算方法、系统及存储介质，下面结合附图对本发明作详细的描述。
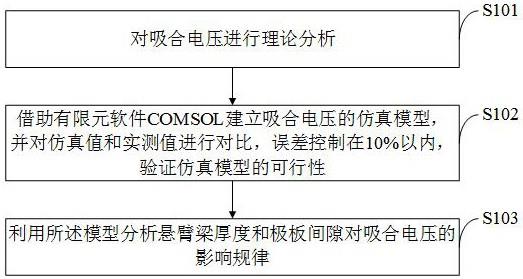
23.如图1所示，本发明实施例提供的静电驱动微执行器吸合电压的计算方法，包括以下步骤：s101，对吸合电压进行理论分析；s102，借助有限元软件comsol建立吸合电压的仿真模型，并对仿真值和实测值进行对比，误差控制在10%以内，验证仿真模型的可行性；s103，利用所述模型分析悬臂梁厚度和极板间隙对吸合电压的影响规律。
24.如图2所示，本发明实施例提供的静电驱动微执行器吸合电压的计算系统包括：吸合电压分析模块1，用于对吸合电压进行理论分析，得电容器存储能量与电容极板距离之间的关系、极板之间的静电吸引力、平衡位置和吸合电压的关系；仿真模型构建模块2，用于借助有限元软件comsol建立吸合电压的仿真模型；仿真模型验证模块3，用于对仿真值和实测值进行对比，误差控制在10%以内，验证所述仿真模型的可行性；模型分析模块4，用于利用所述仿真模型分析悬臂梁厚度和极板间隙对吸合电压的影响规律。
25.下面结合具体实施例对本发明的技术方案作进一步描述。
26.实施例：静电驱动微执行器吸合电压的计算方法1、发明概述：本发明基于静电场和弹性薄板理论，对微机电系统（mems）中常见的静电型悬臂梁式执行器的吸合现象进行了理论分析。借助有限元软件comsol完成了吸合电压的计算并与实际测试结果进行了对比，误差控制在10%以内，验证了该计算模型的可行性。在悬臂梁面积不变的情况下，利用该模型研究了悬臂梁厚度和极板间隙对吸合电压的影响，结果表明厚度和间隙对吸合电压的影响呈非线性规律，可以对后续执行器的设计提供理论依据。
27.在本发明中，首先对吸合电压进行了理论分析，借助有限元软件comsol建立了吸合电压的仿真模型，并对仿真值和实测值进行了对比，误差控制在10%以内，验证了该仿真模型的可行性，利用该模型研究了悬臂梁厚度和极板间隙对吸合电压的影响规律，为执行器在各个领域中的优化提供了理论依据。
28.2、基本理论：如图3所示，静电型微执行器由可动电极5、固定电极6和信号电源7组成。可动电极5和固定电极6之间形成平行板电容，当极板间未施加电压时，可动电极5处于初始位置，执行器处于断开状态；当极板间施加电压时，电容极板进行电荷累积，极板间形成电场，可动电极5在静电力作用下有向下运动的趋势，当静电力达到一定程度时，可动电极5向下弯曲并与信号电源7发生接触，此时信号电源7左右导通，执行器处于导通状态。
29.电容器存储的能量为：
ꢀꢀ
(1)式中电容c为： (2)式中a为两极板交叠面积，ε是真空介电常数，d是极板间初始间隙。
30.根据式(1)、式(2)可得电容器存储能量与电容极板距离之间的关系为：
ꢀꢀ
(3)对上式d求一阶偏导，可得到极板之间的静电吸引力fe为：
ꢀꢀ
(4)在静电吸合过程中，假设电压缓慢变化即不考虑极板的震荡，同时忽略惯性阻尼等因素的影响，可动电极受静电力有向下运动的趋势，则悬臂梁会产生弹性力来与静电力平衡，假设极板间隙减小x，此时系统达到平衡，则：(5)将上式整理成关于x的函数： (6)当系统处于平衡时，做功为零，对式(6)两端分别对x求导得：
ꢀꢀ
(7)最终的平衡位置和吸合电压为：
ꢀꢀ
(8)
ꢀꢀ
(9)由上式可知，可动极板向下运动至间隙1/3处，为静电力和机械回复力平衡的临界位置，如果静电力仍持续增大，两极板将迅速吸合直到接触到一起。
31.3、仿真模型的建立与验证：本发明主要针对mems继电器建立仿真模型，器件主体结构采用单端固定式悬臂梁，悬臂梁主要由镂空的悬簧8、静电驱动极板9和触点10构成，如图4所示，镂空的悬簧8能够使悬臂梁的刚度在一个合理区间内，为mems继电器提供合适的回复力，以保证较低的驱动电压、较高的稳定度以及较小的开断延时，具体地，悬臂梁的端部采用硅与玻璃阳极键合工艺进行，其中悬臂梁的端部是硅材质，与其端部相连的不动面是玻璃材质。
32.针对mems继电器建立有限元模型，采用固体力学+静电模块来模拟静电吸合作用，为保证计算精度，整体网格采用六面体，由于悬臂梁在厚度方向发生变形，因此厚度方向上网格应保证在3层以上，端部采用固定约束，由于受力较小且对整体影响较小，为提高计算效率，此处网格可做粗化处理，整体网格分布如图5所示。
33.对极板电压参数化求解，可获得悬臂梁在不同电压下的应力和位移分布，如图6所示为悬臂梁在指定电压下的应力分布云图，悬臂梁根部应力集中，最大等效应力为3.8mpa，远小于极限值，吸合过程中不会出现永久性变形。当极板位移超过平衡位置时（此处间隙为
1.5μm），两极板会发生迅速吸合，此时极板位移梯度较大，会出现明显拐点，如图7所示，在电压7.8v处端点位移出现明显转折，此时端点位移为0.47μm，与理论值0.5μm比较接近。
34.为验证仿真模型的准确性，需对实际产品进行测试，实际产品微观结构如图8所示。图8为sem（扫描电镜）实拍照片，出自本单位洁净间的光刻区，通过mira3 tescan 泰斯肯牌的扫描电镜获得，涉及参数有：电子束加速电压：5.0千伏；放大倍数：429倍；物镜焦距：33.16毫米；探测模式：二次电子模式（高分辨度立体形貌）；视野范围：1.29毫米。
35.测试设备采用美国semiprobe手动探针台、美国keirhley半导体分析仪，测试方法使用2路探针分别接触继电器驱动电极与输入端，另外2路探针接地，分别连接半导体分析仪的smm1、smm2及接地端，施加电压，使输入电压从0开始增加至继电器动作，并测量规定的工作电压值，测试结果如图9所示。
36.其中，图9中（a）为继电器测试中，吸合电压与工作电压的图形、图像一；图9中（b）为继电器测试中，吸合电压与工作电压的图形、图像二。
37.为保证测量结果的准确性，需对多组产品进行测量并与仿真值进行对比，如图10所示，仿真值与测试值比较接近，最大误差不超过10%，因此该计算吸合电压的仿真模型是可行的。
38.4、吸合电压模型的应用：如本发明前面所提，在面积一定的情况下，吸合电压主要受悬臂梁刚度和极板间隙的影响，为了经济高效的研究其影响规律，本发明借助已经验证的吸合电压仿真模型进行，对影响因素采用控制变量法即其他参数保持不变只改变单一因素的量值，观察吸合电压的变化量。悬臂梁刚度主要受厚度影响，本次主要研究吸合电压随悬臂梁厚度的变化规律，如图11所示，吸合电压随悬臂梁厚度的增加而增大，且呈非线性趋势即随着厚度的增加，吸合电压加速增大而并非均匀增大。
39.吸合电压随极板间隙的变化规律如图12所示，吸合电压随极板间隙的增大而增大，变化规律接近直线，由第二节理论推导可知，吸合电压与间隙的1.5次幂成正比，仿真计算规律同理论公式相接近。
40.5、结论：本发明对静电驱动微执行器的吸合电压进行了理论推导，借助comsol有限元软件建立了吸合电压的仿真模型，并与实际测试进行了对比，误差控制在10%以内，因此建立的仿真模型是可行的。
41.利用仿真模型研究了悬臂梁厚度和极板间隙对吸合电压的影响规律，吸合电压随影响因素的增大呈非线性增长，利用多项式可对变化规律进行拟合，为后续执行器在各种使用环境下的优化提供理论依据。
42.在本发明的描述中，除非另有说明，“多个”的含义是两个或两个以上；术语“上”、“下”、“左”、“右”、“内”、“外”、“前端”、“后端”、“头部”、“尾部”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此不能理解为对本发明的限制。此外，术语“第一”、“第二”、“第三”等仅用于描述目的，而不能理解为指示或暗示相对重要性。
43.在上述实施例中，可以全部或部分地通过软件、硬件、固件或者其任意组合来实现。当使用全部或部分地以计算机程序产品的形式实现，所述计算机程序产品包括一个或多个计算机指令。在计算机上加载或执行所述计算机程序指令时，全部或部分地产生按照
本发明实施例所述的流程或功能。所述计算机可以是通用计算机、专用计算机、计算机网络、或者其他可编程装置。所述计算机指令可以存储在计算机可读存储介质中，或者从一个计算机可读存储介质向另一个计算机可读存储介质传输，例如，所述计算机指令可以从一个网站站点、计算机、服务器或数据中心通过有线（例如同轴电缆、光纤、数字用户线（dsl）或无线（例如红外、无线、微波等）方式向另一个网站站点、计算机、服务器或数据中心进行传输）。所述计算机可读取存储介质可以是计算机能够存取的任何可用介质或者是包含一个或多个可用介质集成的服务器、数据中心等数据存储设备。所述可用介质可以是磁性介质（例如软盘、硬盘、磁带）、光介质（例如dvd）、或者半导体介质（例如固态硬盘solid state disk（ssd））等。
44.以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，都应涵盖在本发明的保护范围之内。