针对新建砌体结构的地震风险控制决策方法

1.本发明涉及地震工程风险评估与控制技术领域，特别是涉及一种针对新建砌体结构的地震风险控制决策方法。


背景技术：

2.砌体结构作为一种历史悠久的结构形式，是我国主要的建筑形式之一。近年来，住房和城乡建设部等15部门发布的《关于加强县城绿色低碳建设的意见》中指出，县城新建住宅以6层为主，6层及以下住宅建筑面积占比应不低于70％。这一规定使得砌体结构重新成为县城新建住宅的主要结构类型。而随着人们生活质量的提升，对新建砌体结构的安全性水平要求也随之增加，即人们愿意支付更多的成本来提升生命安全程度。涉及到地震等自然灾害作用下生命安全风险管理相关的决策可能会对社会公共安全产生重大的影响，因此，工程结构应在经济投资、使用效益、失效时对使用者生命安全保护程度方面达到最佳，如何协调新时代下建筑成本投入和人们支付意愿之间的矛盾是一个重要的研究方向。
3.目前，针对地震作用下建筑结构损失风险分析，主要集中在地震风险评估方面，公开号为cn108957528a的“一种基于地震风险评估的桥梁抗震分析方法”和公开号为cn111160786a的“基于本体的建筑物地震风险性评估方法”的基本思想是根据地震危险性和结构易损性得到结构的地震风险；公开号为cn108957528a的“设定地震风险的性能抗震设计评估方法”，从设定的建筑结构性能水平，在给定性能水平下确定建筑结构的地震需求，结合地震需求的超越概率和地震危险性结合，最终确定地震动输入，建立了一种达到设定性能水准的概率地震风险评估方法。但是，上述文献均针对的是地震导致的结构损失风险评估，目前尚缺少风险控制决策方面的研究。


技术实现要素：

4.基于此，有必要针对上述技术问题，提供一种安全成本投入与降低风险价值相平衡的针对新建砌体结构的地震风险控制决策方法。
5.一种针对新建砌体结构的地震风险控制决策方法，所述方法包括：
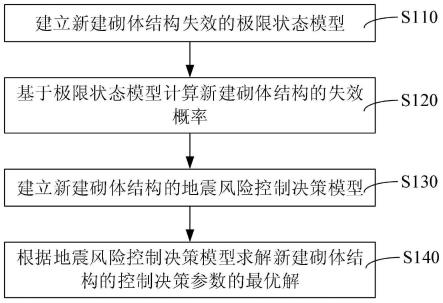
6.建立新建砌体结构失效的极限状态模型；
7.基于所述极限状态模型计算所述新建砌体结构的失效概率；
8.建立所述新建砌体结构的地震风险控制决策模型；
9.根据所述地震风险控制决策模型求解所述新建砌体结构的控制决策参数的最优解。
10.进一步的，所述建立新建砌体结构失效的极限状态模型，之前还包括：
11.确定所述新建砌体结构的控制决策参数，所述控制决策参数包括砂浆强度、楼层数与抗震墙面积率。
12.进一步的，所述新建砌体结构失效的极限状态模型为，
[0013][0014]
式中，z为结构失效的极限状态方程，α为罕遇或设防烈度地震的地震影响系数，因多层砌体结构的自振周期一般在0.1s～0.5s之间，故α取地震影响系数最大值α
max
，n为砌体结构的楼层，λg为重力载荷系数，ρi为i层某方向的抗震墙面积率，ρ’i
为i层另一方向的墙率；f
2,i
为i层砌筑砂浆强度。
[0015]
进一步的，所述基于所述极限状态模型计算所述新建砌体结构的失效概率，包括：
[0016]
确定所述极限状态方程中随机参数的概率分布模型；
[0017]
根据所述随即参数的概率分布模型采用蒙特卡罗法生成随机样本；
[0018]
采用所述随机样本对所述极限状态方程进行计算，得到新建砌体结构的失效概率。
[0019]
进一步的，所述新建砌体结构的地震风险控制决策模型为，
[0020][0021]
式中，t为控制决策参数，τ为时间，dcg/dt表示砌体结构的边际安全成本，c
g,1
表示控制决策参数为t时砌体结构的成本，g为人均国内生产总值，q为消费效用弹性系数，c
x
为人口统计学常数，μ是失效所造成的条件死亡率，n为影响人口规模，pf是结构的失效概率，γs为社会折现率。
[0022]
上述针对新建砌体结构的地震风险控制决策方法，可进行风险控制决策，通过可靠性计算得到不同决策参数时砌体结构的失效概率，通过风险控制决策模型可以得到决策参数的最优解。同时考虑了经济因素对新建砌体结构决策参数的影响和人员安全的影响，平衡考虑了降低风险所投入成本与降低风险所带来利益的关系，可方便有效地确定新建砌体结构控制参数的最优值。
附图说明
[0023]
图1为一个实施例的针对新建砌体结构的地震风险控制决策方法流程图；
[0024]
图2为一个实施例的新建砌体结构平面示意图；
[0025]
图3为图2中实施例的新建砌体结构失效概率与砂浆强度关系的示意图；
[0026]
图4为图2中实施例的风险控制决策方法中决策参数最优解确定示意图。
具体实施方式
[0027]
为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地说明，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0028]
如图1所示，在一个实施例中，一种针对新建砌体结构的地震风险控制决策方法，包括以下步骤：
[0029]
步骤s110，建立新建砌体结构失效的极限状态模型。首先，需要确定新建砌体结构
的控制决策参数，该控制决策参数包括砂浆强度、楼层数与抗震墙面积率等。新建砌体结构失效的极限状态模型，可由以下极限状态方程表示：
[0030][0031]
式中，z为结构失效的极限状态方程，α为罕遇或设防烈度地震的地震影响系数，因多层砌体结构的自振周期一般在0.1s～0.5s之间，故α取地震影响系数最大值α
max
；n为砌体结构的楼层数；λg为重力载荷ge的换算系数，λg＝ge/0.012；ρi为i层某方向的抗震墙面积率(楼层高度1/2处该方向墙体面积a
w,i
与单层建筑面积a0之比)，ρ’i
为i层另一方向的墙率；f
2,i
为i层砌筑砂浆强度。
[0032]
取一栋6层砌体结构，层高3m，结构平面图参见图2。计算方向抗震墙面积率为0.049，正交方向抗震墙面积率为0.084，单位建筑面积重力荷载系数为1.0。抗震设防烈度为7度，设计基本地震加速度值为0.10g(g为重力加速度，g＝9.8m/s2)，多遇地震的α
max
为0.08g。以砂浆强度为新建砌体结构的控制决策参数，则极限状态方程为：
[0033][0034]
步骤s120，基于极限状态模型计算新建砌体结构的失效概率。考虑地震的随机性和结构的随机性，因此极限状态方程中的参数均为随机参数。计算新建砌体结构的失效概率时，参见图2的砌体结构，首先确定极限状态方程中随机参数的概率分布模型，如下表所示：
[0035][0036][0037]
其次，根据随机参数的概率分布模型，采用蒙特卡罗法生成107个随机样本。
[0038]
最后，采用生成的随机样本对极限状态方程进行计算，得到新建砌体结构的失效概率。参见图3，为根据极限状态方程计算图2中砌体结构的失效概率随砂浆强度的变化图。
[0039]
步骤s130，建立新建砌体结构的地震风险控制决策模型。可由以下风险控制决策方程表示：
[0040][0041]
式中，t为控制决策参数，τ为时间，dcg/dt表示砌体结构的边际安全成本，c
g,1
表示控制决策参数为t时砌体结构的成本，g为人均国内生产总值，q为消费效用弹性系数，c
x
为
人口统计学常数，μ是失效所造成的条件死亡率，n为影响人口规模，pf是结构的失效概率，γs为社会折现率。
[0042]
步骤s140，根据地震风险控制决策模型求解新建砌体结构的控制决策参数的最优解。根据风险控制决策方程，确定控制决策参数最优解，如图4所示。图2中砌体结构的砂浆强度不应低于2.65mpa，即采用风险控制决策方法的最优决策参数值为2.65mpa。
[0043]
上述针对新建砌体结构的地震风险控制决策方法，可进行风险控制决策，通过可靠性计算得到不同决策参数时砌体结构的失效概率，通过风险控制决策模型可以得到决策参数的最优解。同时考虑了经济因素对新建砌体结构决策参数的影响和人员安全的影响，平衡考虑了降低风险所投入成本与降低风险所带来利益的关系，可方便有效地确定新建砌体结构控制参数的最优值。
[0044]
以上所述实施例仅表达了本发明的几种实施方式，其描述较为具体和详细，但并不能因此而理解为对本发明专利范围的限制。应当指出的是，对于本领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干变形和改进，这些都属于本发明的保护范围。因此，本发明专利的保护范围应以所附权利要求为准。