一种风电齿轮箱传动系统疲劳性能优化方法

1.本发明涉及风力发电机的技术领域，具体涉及一种风电齿轮箱传动系统疲劳性能优化方法。


背景技术：

2.风电齿轮箱是风电机组传递力与运动的关键传动装置，成本占整机约16％，是风电机组提质增效的关键环节。风电齿轮箱设计寿命通常为20年(陆上)或25年(海上)。
3.现有技术中通常基于单一或多种恒定输入扭矩工况开展齿轮传动系统减振优化设计，但是忽略了因长期风速概率分布造成的风电齿轮箱输入扭矩“短期随机波动”和“长期概率分布”的风电特征。而且，全寿命周期环境参数的随机变化会使风电齿轮箱面临频繁的输入载荷波动，会使风电齿轮箱传动系统出现复杂的载荷波动和结构变形，容易造成齿面载荷分布不均，加剧其接触疲劳失效风险，降低了风电齿轮箱传动系统的使用寿命。


技术实现要素：

4.针对现有技术存在的不足，本发明提出一种风电齿轮箱传动系统疲劳性能优化方法，提高了风电齿轮箱传动系统的疲劳性能。
5.本发明采用的技术方案是一种风电齿轮箱传动系统疲劳性能优化方法。
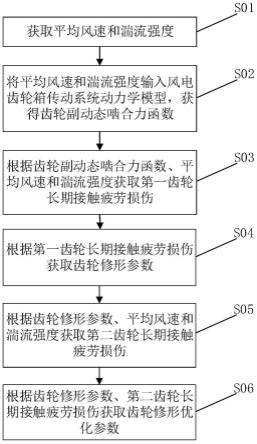
6.在第一种可实现方式中，风电齿轮箱传动系统疲劳性能优化方法，包括：获取平均风速和湍流强度；将平均风速和湍流强度输入风电齿轮箱传动系统动力学模型，获得齿轮副动态啮合力函数；根据齿轮副动态啮合力函数、平均风速和湍流强度获取第一齿轮长期接触疲劳损伤；根据第一齿轮长期接触疲劳损伤获取齿轮修形参数；根据齿轮修形参数、平均风速和湍流强度获取第二齿轮长期接触疲劳损伤；根据齿轮修形参数、第二齿轮长期接触疲劳损伤获取齿轮修形优化参数。
7.结合第一种可实现方式，在第二种可实现方式中，获取平均风速和湍流强度，包括：构建平均风速-湍流强度联合概率密度函数；从平均风速-湍流强度联合概率密度函数中选取平均风速和湍流强度。
8.结合第二种可实现方式，在第三种可实现方式中，根据齿轮副动态啮合力函数、平均风速和湍流强度获取第一齿轮长期接触疲劳损伤，包括：根据齿轮副动态啮合力函数、平均风速和湍流强度获取第一齿轮短期接触疲劳损伤；根据第一齿轮短期接触疲劳损伤、平均风速-湍流强度联合概率密度函数和风电齿轮箱设计寿命获取第一齿轮长期接触疲劳损伤。
9.结合第三种可实现方式，在第四种可实现方式中，齿轮副动态啮合力函数包括齿廓修形、齿廓修形长度和齿向修鼓量，根据齿轮副动态啮合力函数、平均风速和湍流强度获取第一齿轮短期接触疲劳损伤，包括：
10.通过以下公式获取第一齿轮短期接触疲劳损伤：
[0011][0012]
在上式中，u为平均风速，为湍流强度，为低速级太阳轮的齿廓修形量，为低速级太阳轮的齿廓修形长度，为低速级太阳轮的齿向修鼓量，为高速级小齿轮的齿廓修形量，为高速级小齿轮的齿廓修形长度，为高速级小齿轮的齿向修鼓量，σi为水平应力，ni为水平应力σi作用在齿轮的实际次数，c和m为齿轮接触疲劳s-n曲线参数，nb为应力块数量，f(σ)为应力块分布函数，σ为应力块幅值。
[0013]
结合第三种可实现方式，在第五种可实现方式中，根据第一齿轮短期接触疲劳损伤、平均风速-湍流强度联合概率密度函数和风电齿轮箱设计寿命获取第一齿轮长期接触疲劳损伤，包括：
[0014]
通过以下公式获取第一齿轮长期接触疲劳损伤：
[0015][0016]
在上式中，u为平均风速，为湍流强度，为低速级太阳轮的齿廓修形量，为低速级太阳轮的齿廓修形长度，为低速级太阳轮的齿向修鼓量，为高速级小齿轮的齿廓修形量，为高速级小齿轮的齿廓修形长度，为高速级小齿轮的齿向修鼓量，t为风电齿轮箱设计寿命，为平均风速-湍流强度的联合概率密度函数，为第一齿轮短期接触疲劳损伤，u1、u2、和均为实数。
[0017]
结合第一种可实现方式，在第六种可实现方式中，根据第一齿轮长期接触疲劳损伤获取齿轮修形参数，包括：对第一齿轮长期接触疲劳损伤进行回归分析和t检验，筛选出若干类齿轮修形参数。
[0018]
结合第六种可实现方式，在第七种可实现方式中，根据齿轮修形参数、平均风速和湍流强度获取第二齿轮长期接触疲劳损伤，包括：分别从各类齿轮修形参数的范围中确定出各类齿轮修形参数，形成齿轮修形参数组合；分别对平均风速和湍流强度进行抽样，获得环境参数组合工况；根据齿轮修形参数组合和环境参数组合工况获取第二齿轮短期接触疲劳损伤；根据第二齿轮短期接触疲劳损伤获取第二齿轮长期接触疲劳损伤。
[0019]
结合第七种可实现方式，在第八种可实现方式中，根据齿轮修形参数组合和环境参数组合工况获取第二齿轮短期接触疲劳损伤之后，还包括：分别采用克里金模型、多项式响应面模型和径向基函数构建第二齿轮短期接触疲劳损伤的近似函数；获取各近似函数的拟合精度；根据拟合精度选取最优的第二齿轮短期接触疲劳损伤。
[0020]
结合第一种可实现方式，在第九种可实现方式中，根据齿轮修形参数、第二齿轮长期接触疲劳损伤获取齿轮修形优化参数，包括：将各齿轮修形参数处于各齿轮修形参数的预设范围确定为第一约束条件；将各第二齿轮长期接触疲劳损伤小于或等于各第二齿轮长期接触疲劳损伤的极大值确定为第二约束条件；在满足第一约束条件和第二约束条件的情
况下，将第二齿轮长期接触疲劳损伤最小作为优化目标，获取齿轮修形优化参数。
[0021]
结合第九种可实现方式，在第十种可实现方式中，将第二齿轮长期接触疲劳损伤最小作为优化目标，获取齿轮修形优化参数，包括：以第二齿轮长期接触疲劳损伤最小为优化目标，构建风电齿轮箱传动系统长期疲劳损伤优化函数；采用遗传算法对风电齿轮箱传动系统长期疲劳损伤优化函数求解，获得齿轮修形优化参数。
[0022]
由上述技术方案可知，本发明的有益技术效果如下：
[0023]
通过获取平均风速和湍流强度，进而获得齿轮副动态啮合力函数，再根据齿轮副动态啮合力函数、平均风速和湍流强度获取第一齿轮长期接触疲劳损伤，进一步获取第二齿轮长期接触疲劳损伤，根据齿轮修形参数、第二齿轮长期接触疲劳损伤获取齿轮修形优化参数。由于风电齿轮箱传动系统全寿命周期中，平均风速与湍流强度的随机变化会导致齿面载荷分布不均。而本发明考虑到了平均风速与湍流强度的随机变化，通过平均风速和湍流强度获取齿轮修形优化参数，从而使得使用齿轮修形优化参数的风电齿轮箱各级齿轮的齿面载荷分布均匀，在不同风速工况下齿面载荷仍主要集中在齿面中间位置，降低了强风电齿轮箱各级齿轮长期接触疲劳损伤，提高了疲劳性能，提高了风电齿轮箱传动系统的使用寿命。
附图说明
[0024]
为了更清楚地说明本发明具体实施方式或现有技术中的技术方案，下面将对具体实施方式或现有技术描述中所需要使用的附图作简单介绍。在所有附图中，类似的元件或部分一般由类似的附图标记标识。附图中，各元件或部分并不一定按照实际的比例绘制。
[0025]
图1为本发明实施例提供的一种风电齿轮箱传动系统疲劳性能优化方法的示意图；
[0026]
图2为本发明实施例提供的一种优化前后各级齿轮长期接触疲劳损伤对比的示意图。
具体实施方式
[0027]
下面将结合附图对本发明技术方案的实施例进行详细的描述。以下实施例仅用于更加清楚地说明本发明的技术方案，因此只作为示例，而不能以此来限制本发明的保护范围。
[0028]
需要注意的是，除非另有说明，本技术使用的技术术语或者科学术语应当为本发明所属领域技术人员所理解的通常意义。
[0029]
结合图1所示，本实施例提供了一种风电齿轮箱传动系统疲劳性能优化方法，包括：
[0030]
步骤s01、获取平均风速和湍流强度；
[0031]
步骤s02、将平均风速和湍流强度输入风电齿轮箱传动系统动力学模型，获得齿轮副动态啮合力函数；
[0032]
步骤s03、根据齿轮副动态啮合力函数、平均风速和湍流强度获取第一齿轮长期接触疲劳损伤；
[0033]
步骤s04、根据第一齿轮长期接触疲劳损伤获取齿轮修形参数；
[0034]
步骤s05、根据齿轮修形参数、平均风速和湍流强度获取第二齿轮长期接触疲劳损伤；
[0035]
步骤s06、根据齿轮修形参数、第二齿轮长期接触疲劳损伤获取齿轮修形优化参数。
[0036]
可选地，获取平均风速和湍流强度，包括：构建平均风速-湍流强度联合概率密度函数；从平均风速-湍流强度联合概率密度函数中选取平均风速和湍流强度。
[0037]
可选地，平均风速-湍流强度联合概率密度函数如下所示：
[0038][0039]
在公式(1)中，c(
·
,
·
)表示二元copula函数，fv(u)表示10min时序风速的平均风速概率密度函数，fv(u)表示fv(u)的累积分布函数，表示10min 时序风速变化程度的概率密度函数，表示的累积分布函数。
[0040]
在一些实施例中，copula函数是联系变量间多维联合分布和一维边缘分布的一个多元函数，用于研究变量间相依性。
[0041]
在一些实施例中，根据iec61400-1标准(风力发电机组国际设计标准)，平均风速概率密度函数通常服从威布尔分布，即u为平均风速，θ为形状参数，λ为尺度参数。
[0042]
在一些实施例中，概率密度函数通常服从伽马分布，即在一些实施例中，概率密度函数通常服从伽马分布，即在一些实施例中，概率密度函数通常服从伽马分布，即为湍流强度，α为尺度参数，β为形状参数，γ(α)为伽马函数。
[0043]
可选地，从平均风速-湍流强度联合概率密度函数中选取平均风速和湍流强度，包括：采用拉丁超立方抽样法和最大差异法在平均风速-湍流强度联合概率密度函数中进行筛选操作，获得权重占比大于第一预设阈值的平均风速和湍流强度。
[0044]
在一些实施例中，利用二元copula函数c(
·
,
·
)构建平均风速-湍流强度联合概率密度函数，然后采用拉丁超立方抽样法和最大差异法从平均风速-湍流强度联合概率密度函数中选取出权重占比大于第一预设阈值的平均风速和湍流强度的组合工况，以能够在多种平均风速与湍流强度的组合工况下，获取多级齿轮修形参数对风电齿轮箱传动系统长期接触疲劳损伤的影响，提高疲劳性能。
[0045]
可选地，风电齿轮箱传动系统动力学模型包括通过风电机组整机系统动力学模型和风电齿轮箱传动系统动力学模型。
[0046]
在一些实施例中，采用openfast建立风电机组整机系统动力学模型，将openfast进行仿真得到轮毂六自由度载荷.out文件；将载荷.out文件转化为simpack输入.afs文件，利用simpack输入.afs文件和simpack建立风电齿轮箱传动系统动力学模型，对风电机组整机系统动力学模型和风电齿轮箱传动系统动力学模型进行联合仿真，获得风电齿轮箱传动系统的齿轮副动态啮合力函数。然后利用齿轮副动态啮合力函数计算各级齿轮接触疲劳损伤。
[0047]
可选地，齿轮副动态啮合力函数包括齿廓修形、齿廓修形长度、齿向修鼓量。齿廓
修形ek用指数函数曲线形式进行修形；齿廓修形长度λ用长修形方式修形，即λ＝pb(ε
α-1)；齿向修鼓量δ用二次凸函数形式曲线进行修形。在一些实施例中，齿廓修形把原来的渐开线齿廓在齿顶或接近齿根圆角的部位修去一部分，使该处的齿廓不再是渐开线形状，通过齿廓修形使啮合刚度变化比较和缓，减小由于基节误差和受载变形所引起的啮入和啮出冲击，改善齿面润滑状态防止胶合发生。齿向修形是沿齿线方向微量修整齿面，使其偏离理论齿面。齿向修形包括鼓形修整，鼓形修整采用齿向修形使轮齿在齿宽中央鼓起，一般两边呈对称形状。鼓形修整用于改善轮齿接触线上载荷的不均匀分布情况。
[0048]
在一些实施例中，通过建立计入全局载荷的风电齿轮箱传动系统动力学模型；然后获取不同平均风速与湍流强度组合工况；分析不同平均风速与湍流强度组合工况下多级齿轮修形参数对其长期接触疲劳损伤的影响，进而构建“平均风速、湍流强度－齿轮修形参数－长期接触疲劳损伤”映射关系，根据映射关系建立风电齿轮箱传动系统长期疲劳损伤优化函数，对长期疲劳损伤优化函数求解，获得齿轮修形优化参数。由于考虑到了环境参数随机不确定性，考虑到了不同平均风速与湍流强度组合工况，从而保证了风电齿轮箱各级齿轮的齿面载荷分布均匀，在不同风速工况下，齿面载荷仍主要集中在齿面中间位置，提高了工况适应性，降低了强风电齿轮箱各级齿轮长期接触疲劳损伤，疲劳性能提升效果显著。
[0049]
可选地，根据齿轮副动态啮合力函数、平均风速和湍流强度获取第一齿轮长期接触疲劳损伤，包括：根据齿轮副动态啮合力函数、平均风速和湍流强度获取第一齿轮短期接触疲劳损伤；根据第一齿轮短期接触疲劳损伤、平均风速
ꢀ‑
湍流强度联合概率密度函数和风电齿轮箱设计寿命获取第一齿轮长期接触疲劳损伤。
[0050]
可选地，风电齿轮箱设计寿命即为平均风速和湍流强度的组合工况的持续时间。
[0051]
这样，平均风速-湍流强度联合概率密度函数表征平均风速和湍流强度的组合工况出现的概率，风电齿轮箱设计寿命表征平均风速和湍流强度的组合工况的持续时间，二者再结合第一齿轮短期接触疲劳损伤进行计算，获得第一齿轮长期接触疲劳损伤。由于考虑到了平均风速和湍流强度的组合工况出现的概率和持续时间，使得在风电齿轮箱全寿命周期内，避免了风电齿轮箱面临频繁的输入载荷波动，避免了风电齿轮箱传动系统出现复杂的载荷波动和结构变形，使得齿面载荷分布均匀，降低了其接触疲劳失效风险，提高了风电齿轮箱传动系统的使用寿命。
[0052]
可选地，根据齿轮副动态啮合力函数、平均风速和湍流强度获取第一齿轮短期接触疲劳损伤，包括：
[0053]
通过以下公式获取第一齿轮短期接触疲劳损伤：
[0054][0055]
在上述公式(2)中，u为平均风速，为湍流强度，为低速级太阳轮的齿廓修形量，为低速级太阳轮的齿廓修形长度，为低速级太阳轮的齿向修鼓量，为高速级小齿轮的齿廓修形量，为高速级小齿轮的齿廓修形长度，为高速级小齿轮的齿向修鼓量，σi为水平应力，ni为水平应力σi作用在齿轮的实际次数，c和m为齿轮接触疲劳s-n曲线参数，nb为应力块数量， f(σ)为应力块分布函数，σ为应力块幅值。
[0056]
可选地，s-n曲线为其中，c和m为材料常数，σ为应力幅值，n为达到疲劳砍断时的应力循环次数。
[0057]
可选地，根据第一齿轮短期接触疲劳损伤、平均风速-湍流强度联合概率密度函数和风电齿轮箱设计寿命获取第一齿轮长期接触疲劳损伤，包括：
[0058]
通过以下公式获取第一齿轮长期接触疲劳损伤：
[0059][0060]
在上式中，u为平均风速，为湍流强度，为低速级太阳轮的齿廓修形量，为低速级太阳轮的齿廓修形长度，为低速级太阳轮的齿向修鼓量，为高速级小齿轮的齿廓修形量，为高速级小齿轮的齿廓修形长度，为高速级小齿轮的齿向修鼓量，t为风电齿轮箱设计寿命，为平均风速-湍流强度的联合概率密度函数，为第一齿轮短期接触疲劳损伤，u1、u2、和均为实数。可选地，u1＝3m/s，u2＝25m/s，＝25m/s，
[0061]
在一些实施例中，第一齿轮长期接触疲劳损伤的计算过程如下：
[0062][0063]
可选地，根据第一齿轮长期接触疲劳损伤获取齿轮修形参数，包括：对第一齿轮长期接触疲劳损伤进行回归分析和t检验，筛选出若干类齿轮修形参数。
[0064]
在一些实施例中，采用plackett-burman试验设计，结合回归分析和t检验，筛选出对齿轮长期接触疲劳损伤的影响值大于第三预设阈值的齿轮修形变量。可选地，齿轮修形变量为低速级太阳轮、中间级太阳轮和高速级小齿轮的各修形量。可选地，齿轮修形变量
[0065]
因此，第一齿轮长期接触疲劳损伤为：
[0066][0067]
在上式中，分别为低速级太阳轮、中间级太阳轮和高速级小齿轮的齿廓修形量，分别为低速级太阳轮、中间级太阳轮和高速级小齿轮的齿廓修形长度，分别为低速级太阳轮、中间级太阳轮和高速级小齿轮的齿向修鼓量。可选地，u1＝3m/s，u2＝25m/s，＝25m/s，
[0068]
在一些实施例中，plackett-burman试验设计主要通过对每个因子取两水平来进
行分析，通过比较各个因子两水平的差异与整体的差异来确定因子的显著性。t检验是用t分布理论来推论差异发生的概率，从而比较两个平均数的差异是否显著。
[0069]
可选地，根据齿轮修形参数、平均风速和湍流强度获取第二齿轮长期接触疲劳损伤，包括：分别从各类齿轮修形参数的范围中确定出各类齿轮修形参数，形成齿轮修形参数组合；分别对平均风速和湍流强度进行抽样，获得环境参数组合工况；根据齿轮修形参数组合和环境参数组合工况获取第二齿轮短期接触疲劳损伤；根据第二齿轮短期接触疲劳损伤获取第二齿轮长期接触疲劳损伤。
[0070]
可选地，采用蒙特卡洛法分别从各类齿轮修形参数的范围中确定出各类齿轮修形参数，生成若干组齿轮修形参数组合。
[0071]
可选地，采用拉丁超立方抽样法和最大差异法分别对备选平均风速和备选湍流强度进行抽样，生成环境参数组合工况样本矩阵。环境参数组合工况样本矩阵包括若干个环境参数组合工况。
[0072]
在一些实施例中，将齿轮修形参数组合和环境参数组合工况代入公式(2)，获得第二齿轮短期接触疲劳损伤将齿轮修形参数组合和第二齿轮短期接触疲劳损伤代入公式(4)，获得第二齿轮长期接触疲劳损伤如下：
[0073]
可选地，根据齿轮修形参数组合和环境参数组合工况获取第二齿轮短期接触疲劳损伤，还包括：分别采用克里金模型、多项式响应面模型和径向基函数构建第二齿轮短期接触疲劳损伤的近似函数，并检测拟合精度，根据拟合精度将最优的近似函数作为第二齿轮短期接触疲劳损伤。可选地，选择拟合精度大于第二预设阈值的近似函数为最优的近似函数。
[0074]
采用克里金模型、多项式响应面模型和径向基函数构建第二齿轮短期接触疲劳损伤的近似函数，使得近似函数样本附近的近似精度高，随着样本数量的增加，近似精度提高，从而获得更优的第二齿轮短期接触疲劳损伤。
[0075]
在一些实施例中，获取第二齿轮长期接触疲劳损伤的方法如下：
[0076]
步骤s11、采用蒙特卡洛法分别从各类齿轮修形参数pc的范围中确定出各类齿轮修形参数，生成i组齿轮修形参数组合
[0077]
步骤s12、在“外层”采用拉丁超立方抽样法和最大差异法对备选平均风速和备选湍流强度进行抽样，生成环境参数组合工况样本矩阵x|2×m，其中 m为外层样本数量；
[0078]
步骤s13、计算i组齿轮修形变量组合分别在m组环境参数组合工况下的齿轮短期接触疲劳损伤
[0079]
步骤s14、分别采用克里金模型、多项式响应面模型和径向基函数构建第二齿轮短期接触疲劳损伤的近似函数，并检测拟合精度，根据拟合精度选择出最优的近似函数作为第二齿轮短期接触疲劳损伤；
[0080]
步骤s15、将i组齿轮修形参数组合和第二齿轮短期接触疲劳损伤代入公式(4)，获得第二齿轮长期接触疲劳损伤。
[0081]
可选地，根据齿轮修形参数、第二齿轮长期接触疲劳损伤获取齿轮修形优化参数，包括：将各齿轮修形参数处于各齿轮修形参数的预设范围确定为第一约束条件；将各第二齿轮长期接触疲劳损伤小于或等于各第二齿轮长期接触疲劳损伤的极大值确定为第二约束条件；在满足第一约束条件和第二约束条件的情况下，将第二齿轮长期接触疲劳损伤最小作为优化目标，获取齿轮修形优化参数。
[0082]
由于各类齿轮修形参数对改善齿面载荷分布，降低齿轮接触疲劳损伤能力各异，因此，在各齿轮修形参数处于各齿轮修形参数的预设范围的情况下，将第二齿轮长期接触疲劳损伤最小时的齿轮修形参数确定为齿轮修形优化参数，以便从各齿轮修形参数的预设范围确定出一组最优的齿轮修形参数，进而保证了齿轮修形参数在全寿命周期内的各工况下均能达到优化效果，提高了风电齿轮箱传动系统的使用寿命。
[0083]
可选地，齿轮修形参数的预设范围为：齿轮修形参数的极小值≤齿轮修形参数≤齿轮修形参数的极大值。
[0084]
可选地，将各齿轮修形参数处于各齿轮修形参数的预设范围作为第一约束条件；将各第二齿轮长期接触疲劳损伤小于或等于各第二齿轮长期接触疲劳损伤的极大值作为第二约束条件；将第二齿轮长期接触疲劳损伤最小作为优化目标，构建风电齿轮箱传动系统长期疲劳损伤优化函数如下：
[0085][0086]
在上述公式(5)中，x为齿轮修形优化参数，为最小第二齿轮长期接触疲劳损伤，为第j个第二齿轮长期接触疲劳损伤，dj为第j个第二齿轮长期接触疲劳损伤的极大值，，分别为低速级太阳轮、中间级太阳轮和高速级小齿轮的齿廓修形量，分别为低速级太阳轮、中间级太阳轮和高速级小齿轮的齿廓修形长度，分别为低速级太阳轮、中间级太阳轮和高速级小齿轮的齿向修鼓量。；“·”表示变量的极小值，例如表示的极小值；表示变量的极大值，例如表示的极大值。
[0087]
可选地，采用遗传算法对风电齿轮箱传动系统长期疲劳损伤优化函数求解，获得齿轮修形优化参数。
[0088]
风电齿轮箱传动系统长期疲劳损伤优化函数保证了近似函数在全局最优解区域附近的局部近似精度，引导优化过程快速收敛到全局最优解或局部最优解，在每次优化迭代过程中，构造当前代最优解附近的重点空间，并在重点空间内增加样本点，提高近似函数
在真实模型的最优解附近区域的近似精度，进而能够获得更加准确的齿轮修形优化参数。
[0089]
在一些实施例中，将风电齿轮箱传动系统疲劳性能优化方法应用在某兆瓦级风电机组齿轮箱进行仿真验证。图2为优化前后各级齿轮长期接触疲劳损伤对比的示意图。图2中，横坐标为各级齿轮，包括低速级太阳轮、低速级行星轮、低速级内齿圈、中间级太阳轮、中间级行星轮、中间级内齿圈、高速级大齿轮和高速级小齿轮，纵坐标为齿轮长期疲劳损伤；方形黑点折线为优化前的各级齿轮长期接触疲劳损伤折线图；圆形黑点折线为优化后的各级齿轮长期接触疲劳损伤折线图。
[0090]
结合本次仿真验证结果和图2可知：1、优化前的风电齿轮箱各级齿轮的齿面载荷会出现明显的偏载现象，在不同风速工况下其偏载程度存在一定的差异性，容易出现恶劣的周期性边缘接触；优化后的风电齿轮箱各级齿轮的齿面载荷分布在不同风速工况下仍主要集中在齿面中间位置，工况适应性强。2、优化后的风电齿轮箱各级齿轮长期接触疲劳损伤值出现了大幅降低，尤其是高速级大齿轮和小齿轮，最大降幅达37.42％，同时最容易失效的低速级太阳轮长期接触疲劳损伤值降低11.37％，疲劳性能提升效果显著。
[0091]
最后应说明的是：以上实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述各实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分或者全部技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的范围，其均应涵盖在本发明的权利要求和说明书的范围当中。