一种基于自适应阈值ICP算法的点云配准方法

一种基于自适应阈值icp算法的点云配准方法
技术领域
1.本发明涉及三维测量领域，尤其涉及一种基于自适应阈值icp算法的点云配准方法。


背景技术：

2.点云配准一般分为粗配准和精配准两个阶段。点云粗配准结果是将一组稀疏的对应点配准到一起得到的，而每组特征对应点并不能精确对应到完全相同的空间位置，因此粗配准结果的精度并不会是最优的。通常需要在此基础上进行更加精细的几何形状配准，将测量数据与设计数模精确配准到一起。
3.点云精配准问题的求解通常分为对应点匹配与最优刚性变换估计两个过程，通过迭代的进行对应点匹配和最优刚性变换估计，最终完成源点云到目标点云的精确配准。其中对于对应点匹配，最常用的做法是对源点云中的三维点在目标点云中进行最近邻查找，从而得到一系列的近似对应点。最近邻查找结合迭代优化的方式共同构成了经典的icp算法。icp共包含选点、匹配、设权重、误匹配去除、建立误差度量函数和执行优化6个步骤。每个步骤的不同策略选择都会对icp算法的计算效率、收敛情况和配准精度产生影响。对待配准的点云进行采样可以减少最近邻查找的次数，从而降低单次迭代所消耗的时间。但在实际应用中最主要的困难在于——源点云和目标点云的几何形状、重叠程度以及初始位置关系结合。在实际工业零件质量检测应用当中，必须首先确保算法的配准精度，在此前提下还需要兼顾算法的计算效率，并保证算法在不同几何形状、测量数据完整程度和初始位置情况下均具有较好的通用性和稳定性。
4.针对以上问题，本发明提出了一种基于自适应阈值icp算法，通过合理的算法流程划分和自适应距离阈值估计保证了点云精配准的计算效率、收敛范围以及最终精度。


技术实现要素：

5.本为了解决现有技术中的上述缺陷，本发明针对当前工业领域零部件检测中icp算法计算效率和精度的双重需求，提出了一种基于自适应阈值icp算法的点云配准方法，通过合理的算法流程划分和自适应距离阈值估计保证了点云精配准的计算效率、收敛范围以及最终精度。
6.为了实现上述技术效果，本发明通过下述技术方案实现：
7.一种基于自适应阈值icp算法的点云配准方法，包含以下步骤：
8.步骤1.计算集合自适应截断距离；
9.步骤2.计算点距离集合平均值；
10.步骤3.计算点距离集合标准差；
11.步骤4.根据标准差和距离平均值筛选；
12.步骤5.对筛选的对应点进一步计算平均值和标准差；
13.步骤6.计算自适应距离阈值；
14.步骤7.建立距离误差优化目标函数；
15.步骤8.计算均方根误差；
16.步骤9.匹配正确性检验；
17.步骤10.算法收敛判断。
18.步骤1通过每次迭代过程中对应点对距离集合的数据{di，i＝1,2,
……
,n}进行统计分析计算，得到合适的自适应截断距离e，用于icp算法迭代计算中；
19.步骤2对于每次迭代过程中的对应点距离集合{di}，首先计算其平均值，
[0020][0021]
步骤3计算对应点对距离集合的标准差：
[0022][0023]
步骤4按照3σ的原则，根据标准差和距离平均值将对应点对进一步筛选，
[0024]di
∈[μd±
3σd]
[0025]
步骤5筛选得到满足上述条件的对应点对(个数为n)，进一步计算距离均值与标准差
[0026][0027][0028]
步骤6计算自适应距离阈值，
[0029][0030]
步骤7第i次迭代过程中建立了点云p和q之间对应点并去除误匹配后，建立基于最小二乘的距离误差优化目标函数，
[0031]
△
ti＝arg min∑d(rpi+t,qi)
[0032]
其中，d(rpi+t,qi)表示点pi经过旋转变换r和平移变换t后，与点qi之间的距离误差。进一步的，通过利用点到面的距离度量，误差优化目标函数可以表示为，
[0033]
△
ti＝arg min∑||(q
i-rp
i-t)
·
ni||2[0034]
其中，ni为点qi的法向量。
[0035]
步骤8均方根误差计算为：
[0036][0037]
步骤9通过计算均方根误差误差e
rms
是否小于均方根误差阈值，对icp配准正确性进行检验。对于最后一次迭代结果，对应点集为{(pi,qi)，i＝1,2,
……
,nf}，nf为点对数量。点对(pi,qi)的欧式距离记为：
[0038]di
＝||p
i-qi||
[0039]
步骤10前后两次均方根之差的绝对值满足以下条件，icp算法即满足收敛条件
[0040][0041]
本发明的优点在于：
[0042]
本发明提出了一种基于耦合几何和曲率一致性约束的深度图像配准方法，通过耦合几何约束和曲率约束，提升了深度图像配准的精度。通过提出的基于自适应阈值icp算法的点云配准方法，其配准精度较传统icp算法配准精度更高，配准计算效率更高。
附图说明
[0043]
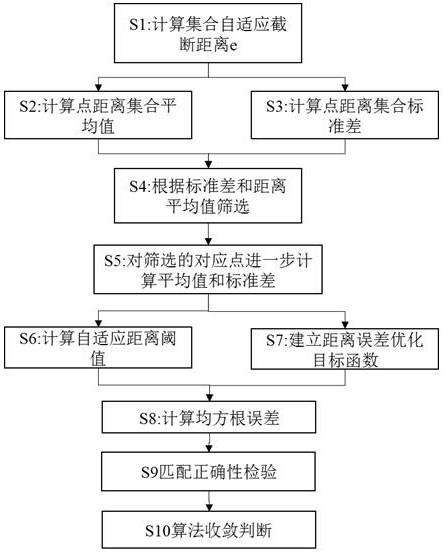
图1为本方法流程示意图。
具体实施方式
[0044]
基于该方法，下面对本发明的实施例做详细说明，本实施例在以本发明技术方案为前提下进行实施，给出了详细的实施方式，但本发明的保护范围不限于下述实施例。
[0045]
实施例1
[0046]
步骤1.计算集合自适应截断距离；
[0047]
步骤2.计算点距离集合平均值；
[0048]
步骤3.计算点距离集合标准差；
[0049]
步骤4.根据标准差和距离平均值筛选；
[0050]
步骤5.对筛选的对应点进一步计算平均值和标准差；
[0051]
步骤6.计算自适应距离阈值；
[0052]
步骤7.建立距离误差优化目标函数；
[0053]
步骤8.计算均方根误差；
[0054]
步骤9.匹配正确性检验；
[0055]
步骤10.算法收敛判断。
[0056]
本发明提出了一种基于耦合几何和曲率一致性约束的深度图像配准方法，通过耦合几何约束和曲率约束，提升了深度图像配准的精度。通过提出的基于自适应阈值icp算法的点云配准方法，其配准精度较传统icp算法配准精度更高，配准计算效率更高。
[0057]
实施例2
[0058]
步骤1通过每次迭代过程中对应点对距离集合的数据{di，i＝1,2,
……
,n}进行统计分析计算，得到合适的自适应截断距离e，用于icp算法迭代计算中；
[0059]
步骤2对于每次迭代过程中的对应点距离集合{di}，首先计算其平均值，
[0060][0061]
步骤3计算对应点对距离集合的标准差：
[0062][0063]
步骤4按照3σ的原则，根据标准差和距离平均值将对应点对进一步筛选，
[0064]di
∈[μd±
3σd]
[0065]
步骤5筛选得到满足上述条件的对应点对(个数为n)，进一步计算距离均值与标准差
[0066][0067][0068]
步骤6计算自适应距离阈值，
[0069][0070]
步骤7第i次迭代过程中建立了点云p和q之间对应点并去除误匹配后，建立基于最小二乘的距离误差优化目标函数，
[0071]
△
ti＝arg min∑d(rpi+t,qi)
[0072]
其中，d(rpi+t,qi)表示点pi经过旋转变换r和平移变换t后，与点qi之间的距离误差。进一步的，通过利用点到面的距离度量，误差优化目标函数可以表示为，
[0073]
△
ti＝arg min∑||(q
i-rp
i-t)
·
ni||2[0074]
其中，ni为点qi的法向量。
[0075]
步骤8均方根误差计算为：
[0076][0077]
步骤9通过计算均方根误差误差e
rms
是否小于均方根误差阈值，对icp配准正确性进行检验。对于最后一次迭代结果，对应点集为{(pi,qi)，i＝1,2,
……
,nf}，nf为点对数量。点对(pi,qi)的欧式距离记为：
[0078]di
＝||p
i-qi||
[0079]
步骤10前后两次均方根之差的绝对值满足以下条件，icp算法即满足收敛条件
[0080][0081]
实施例3
[0082]
一种基于自适应阈值icp算法的点云配准方法，包含以下步骤：
[0083]
步骤1.计算集合自适应截断距离；
[0084]
步骤2.计算点距离集合平均值；
[0085]
步骤3.计算点距离集合标准差；
[0086]
步骤4.根据标准差和距离平均值筛选；
[0087]
步骤5.对筛选的对应点进一步计算平均值和标准差；
[0088]
步骤6.计算自适应距离阈值；
[0089]
步骤7.建立距离误差优化目标函数；
[0090]
步骤8.计算均方根误差；
[0091]
步骤9.匹配正确性检验；
[0092]
步骤10.算法收敛判断。
[0093]
步骤1通过每次迭代过程中对应点对距离集合的数据{di，i＝1,2,
……
,n}进行统计分析计算，得到合适的自适应截断距离e，用于icp算法迭代计算中；
[0094]
步骤2对于每次迭代过程中的对应点距离集合{di}，首先计算其平均值，
[0095][0096]
步骤3计算对应点对距离集合的标准差：
[0097][0098]
步骤4按照3σ的原则，根据标准差和距离平均值将对应点对进一步筛选，
[0099]di
∈[μd±
3σd]
[0100]
步骤5筛选得到满足上述条件的对应点对(个数为n)，进一步计算距离均值与标准差
[0101][0102][0103]
步骤6计算自适应距离阈值，
[0104][0105]
步骤7第i次迭代过程中建立了点云p和q之间对应点并去除误匹配后，建立基于最小二乘的距离误差优化目标函数，
[0106]
△
ti＝arg min∑d(rpi+t,qi)
[0107]
其中，d(rpi+t,qi)表示点pi经过旋转变换r和平移变换t后，与点qi之间的距离误差。进一步的，通过利用点到面的距离度量，误差优化目标函数可以表示为，
[0108]
△
ti＝arg min∑||(q
i-rp
i-t)
·
ni||2[0109]
其中，ni为点qi的法向量。
[0110]
步骤8均方根误差计算为：
[0111][0112]
步骤9通过计算均方根误差误差e
rms
是否小于均方根误差阈值，对icp配准正确性进行检验。对于最后一次迭代结果，对应点集为{(pi,qi)，i＝1,2,
……
,nf}，nf为点对数量。点对(pi,qi)的欧式距离记为：
[0113]di
＝||p
i-qi||
[0114]
步骤10前后两次均方根之差的绝对值满足以下条件，icp算法即满足收敛条件
[0115]