一种不相关并行机调度问题的学习型蜘蛛猴算法

1.本发明涉及计算机集成制造技术领域，特别涉及一种不相关并行机调度问题的学习型蜘蛛猴算法。


背景技术：

2.并行机调度问题(parallelmachineschedulingproblem,pmsp)是将n个工件分配在m台机器上并确定工件在机器上加工顺序，以使得追求的绩效指标最优的问题，是生产调度中一类非常重要的调度优化问题，已被证明是np-hard问题。pmsp中的并行机根据机器特征一般分为等效(identical)机、匀速(uniform)机与不相关(unrelated)机三类。由于企业同类机器的购置时间、价格、加工能力以及供应商等存在差异，不相关并行机(unrelated parallelmachineschedulingproblem，upmsp)在制造过程中更为普遍。目前有关upmsp的研究往往假设机器在制造过程中性能稳定，工件的加工时间固定，然而现实生产中机器的长时间运行磨损和性能恶化等往往会造成生产中断，而且工件的加工时间会随着机器性能或可靠度的下降增加。传统基于静态假设的upmsp研究已不能满足生产现实需求，急需研究考虑预防性维护与恶化效应的不相关并行机调度问题的智能优化算法。
3.在众多智能优化算法中，蜘蛛猴优化(spidermonkeyoptimization，smo)算法根据裂变-融合的社会机制，通过群体分裂来减少个体间的觅食竞争压力以达到寻优目的，具有简单高效的优点，已成为不同领域学者们关注和研究的热点。本发明针对考虑预防性维护与恶化效应的不相关并行机调度问题，以最小化完工时间为目标，提出了一种学习型蜘蛛猴优化(learningsmo，lsmo)算法。


技术实现要素：

4.本发明的目的在于，提供一种不相关并行机调度问题的学习型蜘蛛猴算法。本发明具有针对机器的变周期预防性维护，工件加工时间随机器可靠度变化等动态事件，通过种群个体裂变融合、离散化自适应个体交叉与pm策略知识库构建等快速生成完工时间最小的调度方案，具有提高机器利用率和有效产出的特点。
5.本发明的技术方案：一种不相关并行机调度问题的学习型蜘蛛猴算法；所述具体步骤为：
6.步骤s1：通过混合迭代贪婪规则与随机规则，生成规模为n的初始种群p0；
7.步骤s2：解码计算种群中每个蜘蛛猴个体smh(h＝1,2,
…
,n)的最大完工时间c
hmax
与适应度值fh，对种群进行随机分组确定局部领导者ll与全局领导者gl；
8.步骤s3：判断是否满足终止条件，即达到迭代次数限制，若是，结束，否则，转下一步骤；
9.步骤s4：执行局部领导者更新阶段，运用离散化的交叉方法对各个组内种群个体进行交叉操作，更新每一组种群；
10.步骤s5：执行全局领导者更新阶段，运用离散化的交叉方法对种群个体进行交叉
操作，更新整个种群；
11.步骤s6：执行全局领导者学习阶段，判断全局领导者gl是否有更新，若是，转下一步骤，否则，转步骤s9；
12.步骤s7：执行局部领导者学习阶段，判断局部领导者ll是否有更新，若是，转步骤s10，否则，转下一步骤；
13.步骤s8：若任何局部领导者ll在设定的局部领导者限制次数n
lll
内没有更新，则通过局部领导者决策阶段重新引导组内个体进行更新，转步骤s10；
14.步骤s9：若全局领导者gl在设定的全局领导者限制次数n
gll
内没有更新，则通过全局领导者决策阶段判断是否将种群划分为更小的组或将所有的组融合成一个组；
15.步骤s10：通过预防性维护pm策略知识库指导当前种群p
t
中每个个体的pm决策，进行种群更新；
16.步骤s11：解码计算种群中每个蜘蛛猴个体smh的适应度值fh，确定局部领导者ll与全局领导者gl，令迭代次数t＝t+1，返回步骤s3。
17.上述的不相关并行机调度问题的学习型蜘蛛猴算法中，所述步骤s1中的初始种群生成方法按下述步骤进行：
18.步骤s1.1：问题描述与目标界定，考虑预防性维护的不相关并行机调度问题可以描述为将j＝{j1,j2,
…
,jj…
,jn}中的n个工件安排到m＝{m1,m2,
…
,mi…
,mm}中的m台不相关并行机上，机器mi上分配的工件数量为ni，机器在生产过程中需要进行基于状态的变周期预防性维护，机器的状态用可靠度表示，随着累计加工时间或役龄增加，机器的可靠度降低，工件的加工时间变长，即具有恶化效应；当机器的可靠度低于阈值上限时，工件的实际加工时间增加；一旦机器的可靠度低于阈值下限时，需要实施固定时长的预防性维护才能使机器恢复到初始状态，机器状态变化服从指数型函数，假设机器mi的当前役龄为li，则机器的可靠度用函数表示为λ表示机器故障率；工件jj在机器mi上的基本加工时间为p
ij
，实际加工时间p
′
ij
与机器的可靠度相关，当可靠度处于上限r
th1
与下限r
th2
之间时，实际加工时间按照增长率w成比例增加；若可靠度低于下限r
th2
，实际加工时间为无穷大；实际加工时间与可靠度的关系如下所示：
[0019][0020]
加工过程不可中断，工件的完工时间为cj，维护时长为mt，优化目标为最小化最大完工时间c
max
＝max{cj}，决策内容是确定工件在机器上的分配、工件的加工顺序以及机器的维护时刻；
[0021]
步骤s1.2：根据混合方法中混合迭代贪婪规则以及随机规则的数量比例，即n＝n
ig
+n
random
，按照步骤s1.4与步骤s1.5的方法生成初始种群p0；
[0022]
步骤s1.3：初始化每台机器的完工时间c1＝c2＝
…
＝cm＝0，工件jj在机器mi上的完工时间c
ij
＝0，机器的役龄l1＝l2＝
…
＝lm＝0，每台机器上已调度工件的集合sj1＝sj2＝
…
＝sjm＝φ，未调度工件的集合usj＝{j1，j2，
…
，jn}，设置工件数量n，加工时间增长率w、机器故障率λ、维护时长mt、机器可靠度上限r
th1
、下限r
th2
与种群规模n的参数值，工件指标j＝1，机器指标i＝1，蜘蛛猴个体指标h＝1；
[0023]
步骤s1.4：利用混合迭代贪婪规则生成数量为n
ig
的初始解；
[0024]
步骤s1.5：随机将n个工件分派到m台机器上，生成数量为n
random
的初始解；
[0025]
步骤s1.6：将混合迭代贪婪规则与随机规则生成的初始解合并，构成规模为n＝n
ig
+n
random
的初始种群p0。
[0026]
前述的不相关并行机调度问题的学习型蜘蛛猴算法中，所述步骤s1.4的具体步骤如下：
[0027]
步骤s1.4.1：判断usj＝{φ}是否成立，若是，结束，否则，i＝1，转步骤s1.4.2；
[0028]
步骤s1.4.2：判断i≤m是否成立，若是，j＝1，转步骤s1.4.3，否则，转s1.4.8；
[0029]
步骤s1.4.3：判断j≤|usj|是否成立，若是，转步骤s1.4.4，否则，i＝i+1，转步骤s1.4.2；
[0030]
步骤s1.4.4：计算若r
th1
≤ri≤1，p
′
ij
＝p
ij
，转步骤s1.4.6，否则，转步骤s1.4.5；
[0031]
步骤s1.4.5：若r
th2
≤ri＜r
th1
，p
′
ij
＝p
ij
+w*(r
th1-ri)*p
ij
，转步骤s1.4.6，否则，转步骤s1.4.7；
[0032]
步骤s1.4.6：计算机器役龄li＝li+p
′
ij
，c
ij
＝ci+p
′
ij
，j＝j+1，转步骤s1.4.3；
[0033]
步骤s1.4.7：计算机器役龄li＝p
ij
，c
ij
＝ci+p
ij
+mt，j＝j+1，转步骤s1.4.3；
[0034]
步骤s1.4.8：筛选工件与对应机器满足将工件安排到机器上加工，并更新返回步骤s1.4.1；
[0035]
步骤s1.4.9：循环步骤s1.4.1-步骤s1.4.8，生成数量为n
ig
的初始解。
[0036]
前述的不相关并行机调度问题的学习型蜘蛛猴算法中，所述步骤s2中的解码与适应度计算按下述步骤进行：
[0037]
步骤s2.1：初始化参数，机器mi的完工时间集合机器mi上位置k的完工时间c
i[k]
＝0，工件开始加工前的机器役龄为且工件加工完成后的机器役龄为设置加工时间增长率w，机器故障率λ，机器可靠度上限r
th1
、下限r
th2
与维护时长mt的参数值，种群中蜘蛛猴个体指标h＝1，每个个体中机器指标i＝1，机器上工件数量指标k＝1；
[0038]
步骤s2.2：判断种群数量h＞n是否成立，若是，结束，否则，i＝1，转步骤s2.3；
[0039]
步骤s2.3：判断机器数量i＞m是否成立，若是，得到目标值c
hmax
＝max{c
i[k]
，c
i[k]
∈mc}，适应度值fh＝1/c
hmax
，h＝h+1，返回步骤s2.2，否则，k＝1，转步骤s2.4；
[0040]
步骤s2.4：判断位置k＞ni是否成立，若是，更新mc＝mc∪c
i[k]
，i＝i+1，返回步骤s2.3，否则，转步骤s2.5；
[0041]
步骤s2.5：计算若r
th1
≤ri≤1，p
′
i[k]
＝p
i[k]
，转步骤s2.8，否则，转步骤s2.6；
[0042]
步骤s2.6：若r
th2
≤ri＜r
th1
，p
′
i[k]
＝p
i[k]
+w*(r
th1-ri)*p
i[k]
，转步骤s2.8，否则，转步骤s2.7；
[0043]
步骤s2.7：c
i[k]
＝c
i[k-1]
+p
i[k]
+mt，k＝k+1，返回步骤s2.4；
[0044]
步骤s2.8：c
i[k]
＝c
i[k-1]
+p
′
i[k]
，k＝k+1，返回步骤s2.4。
[0045]
前述的不相关并行机调度问题的学习型蜘蛛猴算法中，所述步骤s4中的局部领导
者更新阶段对各个组内种群个体更新包括如下步骤：
[0046]
步骤s4.1：依次选择种群中的每一个个体，先运用离散化的公式确定小组成员的更新方式，所述离散化的公式如下所示：
[0047][0048]
上述公式给出的局部领导者种群个体交叉更新方法包括第一部分和第二部分；
[0049]
第一部分：
[0050][0051]
上述公式中的g(smh，llk)表示蜘蛛猴个体smh与其所在的第k组的局部领导者llk执行交叉操作，得到新蜘蛛猴个体sm
′h；pr为扰动率，pr＝pr+0.4/t，t为进化次数，pr初始值为0.1；若随机生成的数p
x1
大于pr时，执行交叉操作，否则，保留原个体smh，其中，p
x1
，pr～u(0，1)；
[0052]
第二部分：
[0053]
上述公式中的f(sm
′h，smr)表示蜘蛛猴个体sm
′h与种群中的随机蜘蛛猴个体smr执行交叉操作，p1为交叉概率，若随机生成的数p
x2
小于p1，执行交叉操作；否则，保留原个体sm
′h，其中，p
x2
，p1～u(0，1)；
[0054]
步骤s4.2：根据确定的交叉方式，对局部领导者阶段的组内个体利用两点交叉方法进行更新；如果两个交叉的蜘蛛猴个体编码中存在相同基因位，按照交叉方式1进行交叉，否则，按照交叉方式2进行交叉；
[0055]
交叉方式1：保留父代编码中的相同基因位，其余基因在机器的工件分配方式不变的前提下随机排序；
[0056]
交叉方式2：从每个父代中随机选择长度为[1，n+m-1]的一段基因保留，其余基因位通过映射的交叉方式得到；
[0057]
计算执行交叉操作产生的子代的适应度值，若优于父代个体，保留新个体，否则，保留原来的父代个体，局部领导者未更新次数n
ll
加1。
[0058]
前述的不相关并行机调度问题的学习型蜘蛛猴算法中，所述步骤s5的全局领导者更新阶段对种群个体更新包括如下步骤：
[0059]
步骤s5.1：依次选择种群中的蜘蛛猴个体，根据离散化的公式确定种群个体的更新方式，所述离散化的公式如下所示：
[0060][0061]
上述公式的全局领导者种群个体交叉更新方法包括第一部分和第二部分；
[0062]
第一部分：
[0063][0064]
上述公式中的g(smh，gl)表示蜘蛛猴个体smh与全局领导者gl执行交叉操作，得到新蜘蛛猴个体sm
″h，当随机生成的数p
y1
小于probh，执行交叉操作；否则，保留原个体smh；其中，p
y1
～u(0，1)；上述公式中的probh为蜘蛛猴smh被选中更新的概率，根据个体适应度值计算，计算方法如下所示：
[0065][0066]
其中个体的适应度值计算方法如下所示：
[0067][0068]
第二部分：
[0069][0070]
上述公式中的f(sm
″h，smr)表示蜘蛛猴个体sm
″h与随机蜘蛛猴个体smr执行交叉操作，p2为交叉概率，当随机生成的数p
y2
小于p2，执行交叉操作，否则，保留原个体sm
″h，其中，p
y2
，p2～u(0，1)；
[0071]
步骤s5.2：利用两点交叉的方法对全局领导者更新阶段的种群个体进行更新；如果两个交叉的蜘蛛猴个体编码中存在相同基因位，按照交叉方式1进行交叉，否则，按照交叉方式2进行交叉；
[0072]
交叉方式1：保留父代编码中的相同基因位，其余基因在机器的工件分配方式不变的前提下随机排序；
[0073]
交叉方式2：从每个父代中随机选择长度为[1，n+m-1]的一段基因保留，其余基因位通过映射的交叉方式得到；
[0074]
计算执行交叉操作产生的子代的适应度值，若优于父代个体，保留新个体，否则，保留原来的父代个体，全局领导者未更新次数n
gl
加1。
[0075]
前述的不相关并行机调度问题的学习型蜘蛛猴算法中，所述步骤s10中通过预防性维护策略知识库指导种群个体的pm决策包括如下步骤：
[0076]
步骤s10.1：算法进化前k代的pm策略知识学习阶段；
[0077]
步骤s10.2：算法进化后期通过pm策略知识库中每种策略的执行概率指导蜘蛛猴个体的pm决策；
[0078]
所述pm策略包括pm-ia，pm-ib，pm-ma和pm-mb四种，所述pm-ia的具体步骤如下：
[0079]
步骤a1：按照机器的完工时间对机器进行降序排列，依次找到机器可靠度在[r
th2
，r
th1
)区间没有pm的位置；
[0080]
步骤a2：插入pm；
[0081]
所述pm-ib的具体步骤如下：
[0082]
步骤b1：提取种群中前10％精英个体的pm序列，将可靠度区间[r
th2
，r
th1
)划分为q等分，统计每个子区间qi的pm次数则第q1个子区间执行pm的概率为
[0083]
步骤b2：按照机器的完工时间对机器进行降序排列，依次用轮盘赌的方式选择一个子区间位置插入pm；
[0084]
所述pm-ma的具体步骤如下：
[0085]
步骤c1：按照机器完工时间对机器进行降序排列，依次找到机器可靠度在[r
th1
，1]区间有pm的位置；
[0086]
步骤c2：移除此pm；
[0087]
所述pm-mb的具体步骤如下：
[0088]
步骤d1：选择机器可靠度在[r
th1
，1]区间，且存在pm的位置，按照pm-ib中的方法计算[r
th2
，r
th1
)区间内每个子区间执行pm的概率；
[0089]
步骤d2：按照完工时间对机器进行降序排列，并用轮盘赌的方式选择一个位置，将原pm移动至此。
[0090]
前述的不相关并行机调度问题的学习型蜘蛛猴算法中，所述步骤s10.1的具体步骤如下：
[0091]
步骤s10.1.1：初始化参数，设置种群中所有个体smh执行pm策略s的评分矩阵执行pm策略s的评分矩阵第t代种群p
t
的pm策略评分矩阵设置迭代次数指标t＝1，种群中的蜘蛛猴个体指标h＝1；
[0092]
步骤s10.1.2：判断t＞k是否成立，若是，结束，终止学习，否则，转步骤s10.1.3；
[0093]
步骤s10.1.3：判断h＞n是否成立，若是，计算每种策略下的平均评分并更新c
ts
矩阵，t＝t+1，返回步骤s10.1.2，否则，转步骤s10.1.4；
[0094]
步骤s10.1.4：判断策略数量s＞4是否成立，若是，h＝h+1，返回步骤s10.1.3，否则，转步骤s10.1.5；
[0095]
步骤s10.1.5：对个体smh执行策略s，得到新个体sm
′h，若f
′h＞fh，c
hs
＝c
hs
+1，否则，c
hs
＝c
hs
，令s＝s+1，转步骤s10.1.4。
[0096]
前述的不相关并行机调度问题的学习型蜘蛛猴算法中，所述步骤s10.2的具体步骤如下：
[0097]
步骤s10.2.1：初始化参数，设置个体smh执行策略s的评分矩阵第k代种群pk的维护策略评分矩阵设置迭代次数指标t＝k+1，最大迭代次数maxt；
[0098]
步骤s10.2.2：判断t＞maxt是否成立，若是，结束，否则，计算第t代种群p
t
维护策略s的执行概率转步骤s10.2.3；
[0099]
步骤s10.2.3：根据维护策略的执行概率p
ts
，采用随机遍历抽样方法生成每个个体smh的pm策略，并更新c
hs
，转步骤s10.2.4；所述随机遍历抽样方法是指四种pm策略的概率构成一个轮盘，一次在轮盘上生成n个种群的策略选择，先在[0，1/n]之间产生第一个随机的pm策略选择指针，再以1/n等间隔生成n个策略选择指针；
[0100]
步骤s10.2.4：根据每个蜘蛛猴个体smh执行pm策略s的评分c
hs
计算整个种群执行pm策略的平均评分，并更新到pm策略的评分矩阵c
ts
，令t＝t+1，返回步骤s10.2.2。
[0101]
与现有技术相比，本发明能实现机器需要变周期维护，且加工时间随机器可靠度变化影响下的近优生产调度方案生成，提高车间机器利用率和有效产出。由于不相关并行机调度问题决策变量的离散性，本发明提出了离散化的交叉方法进行局部领导者种群与全
局领导者种群个体的更新；由于动态调度期间工件加工时间和机器维护周期决策的不确定性，本发明设计了基于优秀个体pm策略执行概率的pm策略知识自学习以及基于随机遍历抽样方法的pm策略自决策方法等，避免lsmo算法陷入局部收敛，快速高效地生成近优的调度方案。
附图说明
[0102]
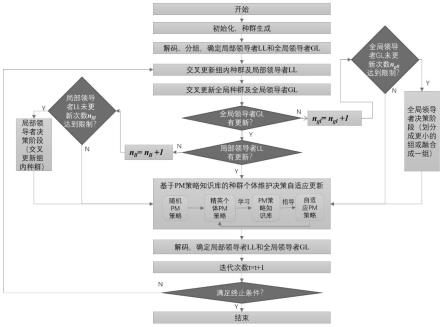
图1是本发明考虑预防性维护的不相关并行机调度问题的学习型蜘蛛猴算法总体流程图；
[0103]
图2是本发明研究问题的示意图；
[0104]
图3是本发明初始解生成流程图；
[0105]
图4是本发明解码示意图；
[0106]
图5是本发明交叉方法1示意图；
[0107]
图6是本发明交叉方法2示意图；
[0108]
图7是本发明预防性维护策略知识库示意图；
[0109]
图8是本发明随机遍历抽样方法示意图；
[0110]
图9是本发明lsmo算法小规模问题的信噪比图；
[0111]
图10是本发明小规模问题不同算法获得的解目标值图；
[0112]
图11是本发明中规模问题不同算法获得的解目标值图；
[0113]
图12是本发明大规模问题不同算法获得的解目标值。
具体实施方式
[0114]
下面结合附图和实施例对本发明作进一步的说明，但并不作为对本发明限制的依据。
[0115]
实施例：一种不相关并行机调度问题的学习型蜘蛛猴算法，如附图1所示，按下述步骤进行：
[0116]
步骤s1：通过混合迭代贪婪规则(iterated greedy，ig)与随机规则，生成规模为n的初始种群p0；
[0117]
所述步骤s1中的初始种群生成方法按下述步骤进行：
[0118]
如附图2所示，步骤s1.1：问题描述与目标界定，考虑预防性维护的不相关并行机调度问题可以描述为将j＝{j1，j2，
…
，ji…
，jn}中的n个工件安排到m＝{m1，m2，
…
，mi…
，mm}中的m台不相关并行机上，机器mi上分配的工件数量为ni，机器在生产过程中需要进行基于状态的变周期预防性维护，机器的状态用可靠度表示，随着累计加工时间或役龄增加，机器的可靠度降低，工件的加工时间变长，即具有恶化效应；当机器的可靠度低于阈值上限时，工件的实际加工时间增加；一旦机器的可靠度低于阈值下限时，需要实施固定时长的预防性维护才能使机器恢复到初始状态，机器状态变化服从指数型函数，假设机器mi的当前役龄为li，则机器的可靠度用函数表示为λ表示机器故障率；工件jj在机器mi上的基本加工时间为p
ij
，实际加工时间p
′
ij
与机器的可靠度相关，当可靠度处于上限r
th1
与下限r
th2
之间时，实际加工时间按照增长率w成比例增加；若可靠度低于下限r
th2
，实际加工时间为无穷大；实际加工时间与可靠度的关系如下所示：
[0119][0120]
加工过程不可中断，工件的完工时间为cj，维护时长为mt，优化目标为最小化最大完工时间c
max
＝max{cj}，决策内容是确定工件在机器上的分配、工件的加工顺序以及机器的维护时刻；
[0121]
如附图3所示，步骤s1.2：根据混合方法中混合迭代贪婪规则以及随机规则的数量比例，即n＝n
ig
+n
random
，按照步骤s1.4与步骤s1.5的方法生成初始种群p0；
[0122]
步骤s1.3：初始化每台机器的完工时间c1＝c2＝
…
＝cm＝0，工件jj在机器mi上的完工时间c
ij
＝0，机器的役龄l1＝l2＝
…
＝lm＝0，每台机器上已调度工件的集合sj1＝sj2＝
…
＝sjm＝φ，未调度工件的集合usj＝{j1，j2，
…
，jn}，设置工件数量n，加工时间增长率w、机器故障率λ、维护时长mt、机器可靠度上限r
th1
、下限r
th2
与种群规模n的参数值，工件指标j＝1，机器指标i＝1，蜘蛛猴个体指标h＝1；
[0123]
步骤s1.4：利用混合迭代贪婪规则生成数量为n
ig
的初始解；
[0124]
所述步骤s1.4的具体步骤如下：
[0125]
步骤s1.4.1：判断usj＝{中}是否成立，若是，结束，否则，i＝1，转步骤s1.4.2；
[0126]
步骤s1.4.2：判断i≤m是否成立，若是，j＝1，转步骤s1.4.3，否则，转s1.4.8；
[0127]
步骤s1.4.3：判断j≤|usj|是否成立，若是，转步骤s1.4.4，否则，i＝i+1，转步骤s1.4.2；
[0128]
步骤s1.4.4：计算若r
th1
≤ri≤1，p
′
ij
＝p
ij
，转步骤s1.4.6，否则，转步骤s1.4.5；
[0129]
步骤s1.4.5：若r
th2
≤ri＜r
th1
，p
′
ij
＝p
ij
+w*(r
th1-ri)*p
ij
，转步骤s1.4.6，否则，转步骤s1.4.7；
[0130]
步骤s1.4.6：计算机器役龄li＝li+p
′
ij
，c
ij
＝ci+p
′
ij
，j＝j+1，转步骤s1.4.3；
[0131]
步骤s1.4.7：计算机器役龄li＝p
ij
，c
ij
＝ci+p
ij
+mt，j＝j+1，转步骤s1.4.3；
[0132]
步骤s1.4.8：筛选工件与对应机器满足将工件安排到机器上加工，并更新返回步骤s1.4.1；
[0133]
步骤s1.4.9：循环步骤s1.4.1-步骤s1.4.8，生成数量为n
ig
的初始解；
[0134]
步骤s1.5：随机将n个工件分派到m台机器上，生成数量为n
random
的初始解；
[0135]
步骤s1.6：将混合迭代贪婪规则与随机规则生成的初始解合并，构成规模为n＝n
ig
+n
random
的初始种群p0；
[0136]
步骤s2：解码计算种群中每个蜘蛛猴个体smh(h＝1，2，
…
，n)的最大完工时间c
hmax
与适应度值fh，对种群进行随机分组确定局部领导者(local leader，ll)与全局领导者(global leader，gl)；
[0137]
如附图4所示，所述步骤s2中的解码与适应度计算按下述步骤进行：
[0138]
步骤s2.1：初始化参数，机器mi的完工时间集合机器mi上位置k的完工时间c
i[k]
＝0，工件开始加工前的机器役龄为且工件加工完成后的机器役龄为设置加工时间增长率w，机器故障率λ，机器可靠度上限r
th1
、下限r
th2
与维护时长mt的参数值，种群中蜘蛛猴个体指标h＝1，每个个体中机器指标i＝1，机器上工件数量指标k＝1；
[0139]
步骤s2.2：判断种群数量h＞n是否成立，若是，结束，否则，i＝1，转步骤s2.3；
[0140]
步骤s2.3：判断机器数量i＞m是否成立，若是，得到目标值c
hmax
＝max{c
i[k]
，c
i[k]
∈mc}，适应度值fh＝1/c
hmax
，h＝h+1，返回步骤s2.2，否则，k＝1，转步骤s2.4；
[0141]
步骤s2.4：判断位置k＞ni是否成立，若是，更新mc＝mc∪c
i[k]
，i＝i+1，返回步骤s2.3，否则，转步骤s2.5；
[0142]
步骤s2.5：计算若r
th1
≤ri≤1，p
′
i[k]
＝[
i[k]
，转步骤s2.8，否则，转步骤s2.6；
[0143]
步骤s2.6：若r
th2
≤ri＜r
th1
，p
′
i[k]
＝p
i[k]
+w*(r
th1-ri)*p
i[k]
，转步骤s2.8，否则，转步骤s2.7；
[0144]
步骤s2.7：c
i[k]
＝c
i[k-1]
+p
i[k]
+mt，k＝k+1，返回步骤s2.4；
[0145]
步骤s2.8：c
i[k]
＝c
i[k-1
]+p
′
i[k]
，k＝k+1，返回步骤s2.4；
[0146]
步骤s3：判断是否满足终止条件，即达到迭代次数限制，若是，结束，否则，转下一步骤；
[0147]
步骤s4：执行局部领导者更新阶段，运用离散化的交叉方法对各个组内种群个体进行交叉操作，更新每一组种群；
[0148]
所述步骤s4中的局部领导者更新阶段对各个组内种群个体更新包括如下步骤：
[0149]
步骤s4.1：依次选择种群中的每一个个体，先运用离散化的公式确定小组成员的更新方式，所述离散化的公式如下所示：
[0150][0151]
上述公式给出的局部领导者种群个体交叉更新方法包括第一部分和第二部分；
[0152]
第一部分：
[0153][0154]
上述公式中的g(smh，llk)表示蜘蛛猴个体smh与其所在的第k组的局部领导者llk执行交叉操作，得到新蜘蛛猴个体sm
′h；pr为扰动率，pr＝pr+0.4/t，t为进化次数，pr初始值为0.1；若随机生成的数p
x1
大于pr时，执行交叉操作，否则，保留原个体smh，其中，p
x1
，pr～u(0，1)；
[0155]
第二部分：
[0156]
上述公式中的f(sm
′h，smr)表示蜘蛛猴个体sm
′h与种群中的随机蜘蛛猴个体smr执行交叉操作，p1为交叉概率，若随机生成的数p
x2
小于p1，执行交叉操作；否则，保留原个体sm
′h，其中，p
x2
，p1～u(0，1)；
[0157]
步骤s4.2：根据确定的交叉方式，对局部领导者阶段的组内个体利用两点交叉方法进行更新；如果两个交叉的蜘蛛猴个体编码中存在相同基因位，按照交叉方式1进行交叉，否则，按照交叉方式2进行交叉；
[0158]
如附图5所示，交叉方式1：保留父代编码中的相同基因位，其余基因在机器的工件分配方式不变的前提下随机排序；
[0159]
如附图6所示，交叉方式2：从每个父代中随机选择长度为[1，n+m-1]的一段基因保
留，其余基因位通过映射的交叉方式得到；
[0160]
计算执行交叉操作产生的子代的适应度值，若优于父代个体，保留新个体，否则，保留原来的父代个体，局部领导者未更新次数n
ll
加1；
[0161]
步骤s5：执行全局领导者更新阶段，运用离散化的交叉方法对种群个体进行交叉操作，更新整个种群；
[0162]
所述步骤s5的全局领导者更新阶段对种群个体更新包括如下步骤：
[0163]
步骤s5.1：依次选择种群中的蜘蛛猴个体，根据离散化的公式确定种群个体的更新方式，所述离散化的公式如下所示：
[0164][0165]
上述公式的全局领导者种群个体交叉更新方法包括第一部分和第二部分；
[0166]
第一部分：
[0167][0168]
上述公式中的g(smh，gl)表示蜘蛛猴个体smh与全局领导者gl执行交叉操作，得到新蜘蛛猴个体sm
″h，当随机生成的数p
y1
小于probh，执行交叉操作；否则，保留原个体smh；其中，p
y1
～u(0，1)；上述公式中的probh为蜘蛛猴smh被选中更新的概率，根据个体适应度值计算，计算方法如下所示：
[0169][0170]
其中个体的适应度值计算方法如下所示：
[0171][0172]
第二部分：
[0173][0174]
上述公式中的f(sm
″h，smr)表示蜘蛛猴个体sm
″h与随机蜘蛛猴个体smr执行交叉操作，p2为交叉概率，当随机生成的数p
y2
小于p2，执行交叉操作，否则，保留原个体sm
″h，其中，p
y2
，p2～u(0，1)；
[0175]
步骤s5.2：利用两点交叉的方法对全局领导者更新阶段的种群个体进行更新；如果两个交叉的蜘蛛猴个体编码中存在相同基因位，按照交叉方式1进行交叉，否则，按照交叉方式2进行交叉；
[0176]
交叉方式1：保留父代编码中的相同基因位，其余基因在机器的工件分配方式不变的前提下随机排序；
[0177]
交叉方式2：从每个父代中随机选择长度为[1，n+m-1]的一段基因保留，其余基因位通过映射的交叉方式得到；
[0178]
计算执行交叉操作产生的子代的适应度值，若优于父代个体，保留新个体，否则，保留原来的父代个体，全局领导者未更新次数n
gl
加1；
[0179]
步骤s6：执行全局领导者学习阶段，判断全局领导者gl是否有更新，若是，转下一步骤，否则，转步骤s9；
[0180]
步骤s7：执行局部领导者学习阶段，判断局部领导者ll是否有更新，若是，转步骤
s10，否则，转下一步骤；
[0181]
步骤s8：若任何局部领导者ll在设定的局部领导者限制次数n
lll
内没有更新，则通过局部领导者决策阶段重新引导组内个体进行更新，转步骤s10；
[0182]
步骤s9：若gl在设定的全局领导者限制次数n
gll
内没有更新，则通过全局领导者决策阶段判断是否将种群划分为更小的组或将所有的组融合成一个组；
[0183]
步骤s10：通过预防性维护(preventive maintenance，pm)策略知识库指导当前种群p
t
中每个个体的pm决策，进行种群更新；
[0184]
如附图7所示，所述步骤s10中通过预防性维护策略知识库指导种群个体的pm决策包括如下步骤：
[0185]
步骤s10.1：算法进化前k代的pm策略知识学习阶段；
[0186]
步骤s10.2：算法进化后期通过pm策略知识库中每种策略的执行概率指导蜘蛛猴个体的pm决策；
[0187]
所述pm策略包括pm-ia，pm-ib，pm-ma和pm-mb四种，所述pm-ia的具体步骤如下：
[0188]
步骤a1：按照机器的完工时间对机器进行降序排列，依次找到机器可靠度在[r
th2
，r
th1
)区间没有pm的位置；
[0189]
步骤a2：插入pm；
[0190]
所述pm-ib的具体步骤如下：
[0191]
步骤b1：提取种群中前10％精英个体的pm序列，将可靠度区间[r
th2
，r
th1
)划分为q等分，统计每个子区间qi的pm次数则第q1个子区间执行pm的概率为
[0192]
步骤b2：按照机器的完工时间对机器进行降序排列，依次用轮盘赌的方式选择一个子区间位置插入pm；
[0193]
所述pm-ma的具体步骤如下：
[0194]
步骤c1：按照机器完工时间对机器进行降序排列，依次找到机器可靠度在[r
th1
，1]区间有pm的位置；
[0195]
步骤c2：移除此pm；
[0196]
所述pm-mb的具体步骤如下：
[0197]
步骤d1：选择机器可靠度在[r
th1
，1]区间，且存在pm的位置，按照pm-ib中的方法计算[r
th2
，r
th1
)区间内每个子区间执行pm的概率；
[0198]
步骤d2：按照完工时间对机器进行降序排列，并用轮盘赌的方式选择一个位置，将原pm移动至此；
[0199]
所述步骤s10.1的具体步骤如下：
[0200]
步骤s10.1.1：初始化参数，设置种群中所有个体smh执行pm策略s的评分矩阵执行pm策略s的评分矩阵第t代种群p
t
的pm策略评分矩阵设置迭代次数指标t＝1，种群中的蜘蛛猴个体指标h＝1；
[0201]
步骤s10.1.2：判断t＞k是否成立，若是，结束，终止学习，否则，转步骤s10.1.3；
[0202]
步骤s10.1.3：判断h＞n是否成立，若是，计算每种策略下的平均评分并更新c
ts
矩阵，t＝t+1，返回步骤s10.1.2，否则，转步骤s10.1.4；
[0203]
步骤s10.1.4：判断策略数量s＞4是否成立，若是，h＝h+1，返回步骤s10.1.3，否则，转步骤s10.1.5；
[0204]
步骤s10.1.5：对个体smh执行策略s，得到新个体sm
′h，若f
′h＞fh，c
hs
＝c
hs
+1，否则，c
hs
＝c
hs
，令s＝s+1，转步骤s10.1.4；
[0205]
所述步骤s10.2的具体步骤如下：
[0206]
步骤s10.2.1：初始化参数，设置个体smh执行策略s的评分矩阵第k代种群pk的维护策略评分矩阵设置迭代次数指标t＝k+1，最大迭代次数maxt；
[0207]
步骤si0.2.2：判断t＞maxt是否成立，若是，结束，否则，计算第t代种群p
t
维护策略s的执行概率转步骤s10.2.3；
[0208]
步骤s10.2.3：根据维护策略的执行概率p
ts
，采用随机遍历抽样方法生成每个个体smh的pm策略，并更新c
hs
，转步骤s10.2.4；如附图8所示，所述随机遍历抽样方法是指四种pm策略的概率构成一个轮盘，一次在轮盘上生成n个种群的策略选择，先在[0，1/n]之间产生第一个随机的pm策略选择指针，再以1/n等间隔生成n个策略选择指针；
[0209]
步骤s10.2.4：根据每个蜘蛛猴个体smh执行pm策略s的评分c
hs
计算整个种群执行pm策略的平均评分，并更新到pm策略的评分矩阵c
ts
，令t＝t+1，返回步骤s10.2.2；
[0210]
步骤s11：解码计算种群中每个蜘蛛猴个体smh的适应度值fh，确定局部领导者ll与全局领导者gl，令迭代次数t＝t+1，返回步骤s3。
[0211]
为了验证本技术提出方法的lsmo算法的有效性，结合某制造型企业的不相关并行机生产场景，设计了如表1所示的问题实验环境。实验环境包括机器参数、工件参数及pm活动相关参数。机器参数为机器数量m；工件参数包括工件数量n，基本加工时间p
ij
；pm活动参数包括维护时间mt，设备故障率λ。
[0212]
表1仿真实验的问题参数
[0213][0214]
从表1所示的实验问题中选择15个典型实例，通过信噪比分析确定学习型蜘蛛猴算法的参数值。针对影响蜘蛛猴算法绩效的四个参数：种群数目n，最大迭代次数maxt，局部领导者更新阶段交叉率p1与全局领导者更新阶段交叉率p2，通过预实验确定的取值范围如表2所示。
[0215]
表2学习型蜘蛛猴算法的参数和取值范围
[0216][0217]
将4个影响参数作为控制因子，每个因子4个水平，正交试验的次数为l16(44)。将最小化完工时间作为响应列，每组参数组合之下实验10次，总实验次数为16
×
15
×
10＝2400次。针对小规模问题的实验结果如表3所示。小规模问题的信噪比图如附图9所示。
[0218]
表3小规模问题的参数实验结果
[0219][0220]
按照同样的方法对比较算法ga与smo算法的参数进行信噪比分析，最终确定的lsmo算法以及ga算法与smo算法的实验参数如表4所示。
[0221]
表4 lsmo算法以及sa算法与smo算法的实验参数
[0222][0223][0224]
利用表4确定的算法参数以及表1确定的问题参数进行实验，每组实例问题进行10次实验，比较不同算法的运行时间和求解质量。三种算法针对不同规模问题的平均运行时间如表5-7所示。从最优解min、最差解max与平均值avg三个指标比较的不同算法的求解质量如附图10-12所示。
[0225]
表5小规模问题的平均运行时间(单位：s)
[0226][0227]
表6中规模问题的平均运行时间(单位：s)
[0228][0229][0230]
表7大规模问题的平均运行时间(单位：s)
[0231][0232]
从总体来看，随着问题的复杂度增加，三种算法平均运行时间随着问题规模的增加呈现增长的趋势。其中lsmo算法平均运行时间最长，ga算法平均运行时间最短。原因是smo算法整体流程上相较ga算法更为复杂，所需的流程时间会更多。而lsmo算法平均运行时间多于smo算法的原因在于lsmo算法在smo算法的基础上增加了ig算法生成初始种群方式与pm概率知识库。
[0233]
对于三种算法获得的解质量，当问题规模较小时，由于问题的解空间相对较小，三种算法几乎都能找到最优解或近优解，三种算法在三种目标值指标(min、max与avg)的取值几乎没有差异。随着问题规模的增加(工件与机器数量增加)，问题的复杂度增加，lsmo算法获得的解质量最好，其次是smo算法，最后是ga算法。随着问题规模的变大，lsmo算法的优势越明显，对于大规模问题，lsmo算法获得的目标值的max指标甚至小于ga算法和smo算法的min指标的趋势。原因是smo算法基于裂变-融合的寻优机制，有利于算法跳出局部最优，获得更好的解，因此smo算法总体上表现出的求解质量优于ga算法。lsmo算法中启发式规则生成初始种群的方式使得算法在初始搜索空间优于其他算法；增加了pm知识库从pm决策的方式改进了解质量。
[0234]
综合三种算法的运行时间与运行质量，可以发现lsmo算法可以快速求解具有动态事件的不相关并行机调度问题。