一种赋形方向图综合方法与流程

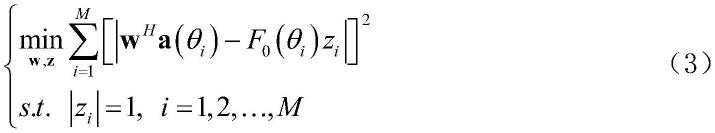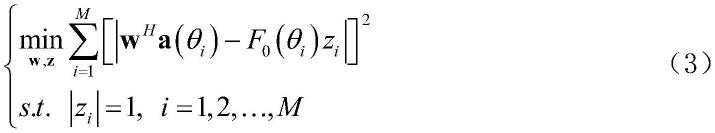
1.本发明属于阵列信号处理领域，具体涉及一种基于幅度最小二乘模型和半正定松弛的赋形方向图综合方法。


背景技术：

2.阵列天线的赋形方向图综合本质上是调整各阵元激励的幅度和相位，使得天线的方向图逼近期望的赋形方向图。目前比较经典的方法有以下几种：
3.elliott提出了基于谢昆诺夫单位圆的综合方法，但该方法只能限制部分旁瓣的电平；
4.李欣等人提出了基于broyden-fletcher-goldfarb-shannon(bfgs)算法的综合方法，但该方法容易陷入局部最优解；
5.fuchs提出了基于凸松弛的综合方法，但该方法鲁棒性较差，在给定的方向图模板不合适时，无法找到可行解。
6.上述方法除了可能无法获得期望的方向图外，在阵列规模较大时，求解复杂度也比较高，因为其所求解的维度与阵元个数成正比。


技术实现要素：

7.本发明的目的是提供一种赋形方向图综合方法，该方法基于幅度最小二乘模型和半正定松弛，解决了现有方法存在的求解不稳定以及求解复杂度高的问题。
8.为了实现上述目的，本发明所采用的技术方案是：
9.一种赋形方向图综合方法，包括以下步骤：
10.(1)建立赋形方向图综合方法的幅度最小二乘模型；
11.(2)通过引入辅助变量的方式将步骤(1)建立的模型等价转换为一个约束优化问题；
12.(3)通过分层优化的方式将步骤(2)转换的问题简化为一个关于辅助变量的约束优化问题，并得到自变量和辅助变量的等量关系；
13.(4)利用半正定松弛求解关于辅助变量优化问题的最优解，通过自变量和辅助变量的等量关系得到自变量的最优解。
14.进一步的，步骤(1)的具体方式为：
15.对于由n个阵元组成的线性天线阵列，其方向图阵因子为
16.s(θ)＝wha(θ)
ꢀꢀꢀ
(1)
17.其中，w为阵列的复激励向量，包含各阵元激励的幅度和相位，a(θ)为阵列的导向矢量，上标h表示共轭转置；线性天线阵列的赋形方向图综合是通过调整激励的幅度和相位来逼近期望的赋形方向图的，由此，构建如下幅度最小二乘模型：
18.19.其中，θi为角度采样值，f0(θi)为期望方向图的采样值，m为采样点的个数。
20.进一步的，步骤(2)的具体方式为：
21.幅度最小二乘模型式(2)等价于下式：
[0022][0023]
其中，z为引入的辅助变量；令d＝diag{f0(θ)}，将式(3)改写为矩阵形式：
[0024][0025]
其中，a＝[a(θ0) a(θ1)
ꢀ…ꢀ
a(θm)]h。
[0026]
进一步的，步骤(3)中，通过分层优化的方式对式(4)进行求解，具体方式为：
[0027]
式(4)等价于
[0028][0029]
内层优化问题的最优解为最小二乘解，即
[0030][0031]
其中，为a的伪逆矩阵；把式(6)代入式(5)，得
[0032][0033]
由于为投影矩阵，根据投影矩阵的幂等性，将式(7)等价为下式：
[0034][0035]
其中，
[0036]
进一步的，步骤(4)中，通过半正定松弛方法进行求解，具体方式为：
[0037]
式(8)等价于
[0038]
[0039]
其中，z＝zzh；
[0040]
式(9)仅有秩1约束是非凸的，忽略该约束，则将式(9)松弛为：
[0041][0042]
式(10)为一个标准的凸优化问题，通过cvx工具对其进行求解，得到最优的z，通过特征值分解得到最优的秩1向量z；
[0043]
得到辅助变量的最优解后，根据式(6)，得到激励向量的最优解。
[0044]
本发明的有益效果是：
[0045]
1.通过幅度最小二乘模型来进行赋形方向图综合，可以在给定的期望方向图模板不合适时，也能找到一组解，使得实现的方向图逼近期望方向图。
[0046]
2.通过引入辅助变量，将求激励向量的最优解转化为求辅助变量的最优解，而辅助变量的维度仅与期望方向图采样点的个数有关，与阵列规模无关，因此，在阵列规模较大时，本发明可以通过非均匀角度采样的方式来降低求解的复杂度，从而提高计算效率。
附图说明
[0047]
图1为本发明实施例的线性天线阵列(ula)图；
[0048]
图2为本发明实施例设置旁瓣电平为-26db时实现的赋形方向图；
[0049]
图3为本发明实施例设置旁瓣电平为-30db时实现的赋形方向图；
[0050]
图4为本发明实施例设置旁瓣电平为-40db时实现的赋形方向图。
具体实施方式
[0051]
下面，结合附图和具体实施方式对本发明做进一步的说明。
[0052]
一种赋形方向图综合方法，该方法基于幅度最小二乘模型和半正定松弛。首先建立赋形方向图综合算法的幅度最小二乘模型；然后通过引入辅助变量的方式将问题等价转换为一个约束优化问题；接下来通过分层优化的方式将问题简化为一个关于辅助变量的约束优化问题，并得到了自变量和辅助变量的等量关系；最后，利用半正定松弛求解关于辅助变量优化问题的最优解，并通过自变量和辅助变量的等量关系得到自变量的最优解。具体如下：
[0053]
步骤1，建立赋形方向图综合的幅度最小二乘模型
[0054]
假设有一由n个阵元组成的ula阵列，如图1所示，其方向图阵因子为
[0055]
s(θ)＝wha(θ)
ꢀꢀꢀ
(1)
[0056]
其中，w为阵列的复激励向量，包含各阵元激励的幅度和相位，a(θ)为阵列的导向矢量。ula阵列的赋形方向图综合是通过调整激励的幅度和相位来逼近期望的赋形方向图的，因此可以构建如下幅度最小二乘模型：
[0057]
[0058]
其中，θi为角度采样值，f0(θi)为期望方向图的采样值，m为采样点的个数。此处为了提高计算效率，可以采用非均匀采样的方式。
[0059]
步骤2，问题的等价转换
[0060]
式(2)等价于
[0061][0062]
其中，z为引入的辅助变量。令d＝diag{f0(θ)}，可将式(3)改写为矩阵形式
[0063][0064]
其中，a＝[a(θ0) a(θ1)
ꢀ…ꢀ
a(θm)]h。
[0065]
步骤3，分层优化
[0066]
式(4)可以通过分层优化的方式求解。式(4)等价于
[0067][0068]
内层优化问题的最优解为最小二乘解，即
[0069][0070]
其中，为a的伪逆矩阵。把式(6)代入式(5)可得
[0071][0072]
由于为投影矩阵，根据投影矩阵的幂等性，式(7)等价于
[0073][0074]
其中，
[0075]
步骤4，半正定松弛求解。
[0076]
式(8)可以通过半正定松弛技术求解。式(8)等价于
[0077][0078]
其中，z＝zzh。式(9)仅有秩1约束是非凸的，忽略该约束，可将式(9)松弛为
[0079][0080]
式(10)为一个标准的凸优化问题，可以通过cvx求解。此处，为了得到一个低秩矩阵，可以利用启发式规则，如式(11)所示
[0081][0082]
其中，δ为正则化系数，一般取一个小的正数。由于式(11)为一个多目标优化问题，可以通过加权的方式转化为一个单目标优化问题
[0083][0084]
其中，λ为非负的加权系数。在得到最优的z，可以通过特征值分解得到最优的秩1向量z。
[0085][0086]
其中，σ1为最大的特征值，u1为对应的特征向量。
[0087]
步骤5，最优的激励向量求解。
[0088]
在步骤4得到辅助变量的最优解后，根据式(6)，可得激励向量的最优解。
[0089]
下面为一个更具体的例子：
[0090]
本实施例为一个20阵元的均匀线阵，阵元间距为工作频率对应的半波长；采用本发明设计波束中心在90
°
，波束宽度为40
°
的平顶方向图，其中主瓣区域为[70
°
,110
°
]，主瓣电平设置为0db，旁瓣区域为[0
°
,70
°
]∪[110
°
,180
°
]，旁瓣电平分别设置为-26db，-30db，-40db。通过式(2)-式(13)可求得最优的激励向量，以此计算出的方向图，如图2～图4所示，
即使在设置的旁瓣电平不合适时，也能接近期望的赋形方向图。
[0091]
总之，本发明通过幅度最小二乘模型和半正定规划实现赋形方向图的综合，鲁棒性较好，而且在引入辅助变量后，可以通过非均匀角度采样降低求解复杂度，提高计算效率。