一种基于图神经网络的阶段式错误定位方法

1.本发明涉及软件测试技术领域，具体涉及到软件错误定位，提供了一种基于图神经网络的错误定位方法，以达到提高错误定位准确率的目的。


背景技术：

2.在软件开发中，调试一直是一个耗时、耗力且乏味的过程。研究发现，在一些项目中，调试可以占到开发时间的80％。为了减少调试过程的时间开销，研究人员提出了自动错误定位技术，旨在通过自动识别潜在的故障位置来减少调试的时间开销。
3.目前，基于频谱的错误定位技术(sbfl)是使用最广泛使用的一类自动错误定位技术。sbfl技术通过分析程序频谱来计算程序实体(如语句、基本块和函数)的怀疑度分数，然后再对其进行排名。程序频谱记录了与程序实体执行有关的信息。对于一个程序实体s，其程序频谱可以表示为一个四元组(ef,e
p
,nf,n
p
)。其中，ef为执行了s且执行失败的测试用例数，e
p
为执行了s且执行成功的测试用例数，nf为没有执行s且执行失败的测试用例数，n
p
为没有执行s且执行成功的测试用例数。频谱可以通过错误定位公式转换为怀疑度分数。通常来说，由更多失败的测试用例执行的程序实体比由更多成功的测试用例执行的程序实体更可疑。近年来，许多基于不同假设的基于频谱的错误定位方法被提出，如提出了新的错误定位公式的ochiai和jaccrad以及使用机器学习的方法来综合现有错误定位技术的multric。然而，因为sbfl技术依赖于程序频谱来计算怀疑度，因此，sbfl无法区分具有相同程序频谱的程序实体。
4.程序结构对于分析和理解程序至关重要。近年来，在程序结构中，控制流反映了程序实体的执行顺序，数据流记录了变量的定义和使用，反映了程序实体之间的数据依赖关系。然而，基于频谱的错误定位方法大都将程序实体视为孤立的个体，而没有考虑它们之间的关系。因此，我们提出了基于图神经网络的错误定位方法，它将已有sbfl计算来的怀疑度分数与函数图结构相结合，并通过图神经网络进行计算，以对具有相同频谱的语句进行区分从而进行精确定位。
5.在定位方式上，本发明采用了两阶段的定位策略。目前，最常用的两种定位策略分别是语句级定位和函数级定位。语句级定位基于语句粒度，按照语句的怀疑度分数给出一个语句级的排序列表，函数定位则是基于函数粒度，按照函数的怀疑度分数给出一个函数级别的排序列表。一般认为，语句级的错误定位过于精细，因为排序列表中相邻的语句在程序中往往相距甚远，例如在两种不同的函数，甚至两个不同的文件中。这就导致开发人员按此列表检查时跨度很大，常常需要反复检查不同的函数或文档，缺少连贯性。函数定位则比较粗略，开发者无法获得任何函数内提示。因此，与之前的错误定位策略不同，本发明采用两阶段定位策略，首先给出了一个函数级别的排序列表，然后当开发者检查某一个函数时，再动态生成该函数内各语句的语句级排序列表，这样可以给开发者提供更多充分有效的信息，有利于提高错误定位的效率。
6.同时，为了减少提取程序图结构以及使用图神经网络进行计算而带来的额外时间
开销，本发明采用了tarantula-dnn-gnn分级加速策略，本发明并非对有所函数都使用gnn进行计算，而是先使用tarantula技术对函数进行初步排序，再依次使用dnn和更复杂的gnn模型对排名靠前的函数进行进一步排序，从而减少因使用图神经网络而带来的时间开销。


技术实现要素：

7.技术问题：本发明提出了一种基于图神经网络的阶段式错误定位方法，该方法可以提高sbfl技术的定位精度。
8.技术方案：本发明是一种基于图神经网络的阶段式错误定位方法，通过分析程序函数中语句的控制流信息和数据依赖信息，提取程序函数的控制流图和数据依赖图，利用图神经网络来学习函数内语句之间的内在关系，通过引入图结构信息来解决传统sbfl技术无法区分相同频谱的程序实体的问题，从而提高定位精度；本发明将定位过程分为两个阶段，先后给出函数级别以及函数内语句级别的排序列表，更符合开发者的使用习惯；为了减少时间开销，本发明采用一种tarantula-dnn-gnn分级加速策略，从而提高定位效率。
9.该方法以函数图为基本单位，将基于频谱的错误定位技术sbfl与图神经网络gnn相结合，且将定位分为两阶段，即函数级定位以及函数内部语句级定位，并在定位过程中使用分级加速策略以高效且准确地定位错误，该方法具体包含的步骤为：
10.步骤1，使用包含至少一个失败用例的测试用例集测试包含缺陷的目标程序，分别统计目标程序在语句级别和函数级别的频谱信息；并筛选出至少覆盖过一个失败错误用例的函数放入第一待排函数集m1；
11.步骤2，对于第一待排函数集m1的所有函数，采用tarantula公式计算各函数语句的怀疑度分数，并取函数内语句的怀疑度的最大值作为函数的怀疑度，随后将各函数按其怀疑度大小从高到低进行排序，之后，选取排名前50的函数放入待第二排函数集m2以待进一步的排序；
12.步骤3，使用多种怀疑度计算公式计算第二待排函数集m2中各函数内所有语句的怀疑度分数，并组合成怀疑度向量，使用训练好的全连接神经网络dnn计算m2中各函数的怀疑度，并将各函数按由dnn计算来的怀疑度分数从高到低排序，之后，选取排名前10的函数放入第三待排函数集m3以待更精确的排序；
13.步骤4，对第三待排函数集m3中的所有函数进行静态分析，抽取各函数的控制流图和数据依赖图，并综合各函数内语句的怀疑度向量得到各函数特征图；
14.步骤5，将步骤4得到的函数特征图两两输入到训练好的基于图神经网络的排序模型进行更精确的排序，至此所有函数都已排序，得到程序函数的排序列表，按照此列表逐一检查直至排查到错误函数；
15.步骤6，当按步骤5得到的排序列表检查至任意函数m时，将m的函数特征图输入到训练好的节点预测图神经网络进行二阶段错误定位，得到m中各语句按怀疑度大小由高到低排序的列表，通过此列表的提示来尽快定位到函数内缺陷语句。
16.其中，
17.步骤1中对于目标程序任意语句s，其频谱信息定义为四元组(ef,e
p
,nf,n
p
)，其中，ef为执行了s且执行失败的测试用例数，e
p
为执行了s且执行成功的测试用例数，nf为没有执行s且执行失败的测试用例数，n
p
为没有执行s且执行成功的测试用例数。
18.步骤1中对于任意函数m：其频谱信息定义为四元组(ef,e
p
,nf,n
p
)，其中，ef为执行了m且执行失败的测试用例数，e
p
为执行了m且执行成功的测试用例数，nf为没有执行m且执行失败的测试用例数，n
p
为没有执行m且执行成功的测试用例数。
19.步骤1中筛选出至少覆盖过一个失败错误用例的函数，将所有ef≠0的函数放入第一待排函数集m1中，未放入第一待排函数集m1中的函数被视为与错误无关。
20.步骤3中使用多种怀疑度计算公式计算各语句的怀疑度分数并组合成怀疑度向量，具体为：对第二待排函数集m2内的每一个函数m的每一条语句s，使用多个经典错误定位公式计算其怀疑度，并拼接成怀疑度向量v。
21.步骤4中对第三待排函数集m3中的所有函数进行静态分析，抽取每一个函数的控制流图g
cfg
和数据依赖图g
ddg
，并综合各函数内语句的怀疑度向量得到各函数的特征图；对第三待排函数集m3内的每一个函数m，其控制流图以邻接矩阵c表示，其大小为a
×
a，其中，a为函数m中有效代码的行数；该矩阵第i行j列的值c
ij
表示控制流的流经情况；若c
ij
为1表示有控制流自此函数第i条语句流向此函数第j条语句，若c
ij
为0则表示没有控制流自此函数第i条语句流向此函数第j条语句；数据依赖图以邻接矩阵d表示，其大小亦为a
×
a，该矩阵第i行j列的值表示程序语句的数据依赖情况；若为1表示第i条语句依赖于第j条语句定义或修改的数据，若为0则表示第i条语句不依赖于第j条语句定义或修改的数据；之后，综合得到的控制流图g
cfg
、数据依赖图g
ddg
、以及m内各语句对应的怀疑度向量，获得函数m的函数特征图特征图特征图代表g中所有的节点，每个节点代表函数m中的一条语句，ε代表g中所有的边，边代表语句之间的关系；代表g中边的种类，边种类总共包含四种，分别是数据流流入，数据流流出，控制流流入以及控制流流出；代表g的特征矩阵，代表第i个节点的特征，其值为步骤3中得到的怀疑度向量。
22.步骤5所述排序，使用快速排序作为整体排序框架，使用训练好的基于图神经网络的排序模型来比较任意两个函数的怀疑度大小；该模型由图嵌入层和全连接层两部分组成，图嵌入层用来提取函数图的特征，全连接层来比较提取出的特征的怀疑度大小，输入为两个特征图g1和g2，输出结果代表g1和g2谁更可能是错误位置。
23.步骤6进行二阶段错误定位，得到函数m中各语句按怀疑度大小由高到低排序的列表，将函数特征图输入到训练好的对边权重敏感的节点预测图神经网络，得到各节点为缺陷节点的概率，按照其概率大小进行排序得到函数内语句怀疑度排序列表。
24.其中，与一阶段的模型不同，二阶段模型考虑了图中各边的权重。边权重通过将边的频谱输入到一个训练好的神经网络得到，其中，边的频谱与语句频谱类似，反映了该边在执行过程中的覆盖信息。
25.有益效果：本发明与现有技术相比，其显著优点是：通过使用图神经网络来捕捉程序函数内语句之间的联系，并将函数内语句间的联系与语句的怀疑度向量相结合，从而进一步提高错误定位地准确率；利用图神经网络既可以进行图嵌入也可以进行节点嵌入的优点，以程序函数图为基本单位，使用基于图神经网络的模型来进行分阶段的错误定位，先进行函数级别的定位，再进行函数内语句级别的定位，更加符合真实场景下开发者排查缺陷时的习惯；通过提取程序各函数的依赖关系而不是整个程序的依赖关系，且采用tarantula-dnn-gnn分级加速策略，有效提高计算效率。
附图说明
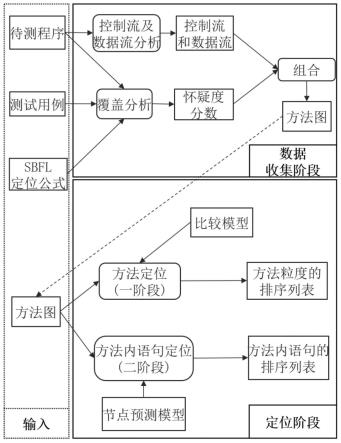
26.图1为基于图神经网络的阶段式错误定位方法流程图，
27.图2为tarantula-dnn-gnn分级加速策略示意图，
28.图3为函数特征图示意图，
29.图4为一阶段模型示意图，
30.图5为二阶段模型示意图。
具体实施方式
31.本发明是一种基于图神经网络的阶段式错误定位方法，通过分析了程序函数中语句的控制流信息和数据依赖信息，提取了程序函数的控制流图和数据依赖图，利用图神经网络来学习函数内语句之间的内在关系，通过引入图结构信息来解决传统sbfl技术无法区分相同频谱的程序实体的问题，从而提高定位精度；本发明将定位过程分为两个阶段，先后给出函数级别以及函数内语句级别的排序列表，更符合开发者的使用习惯；为了减少时间开销，本发明采用一种tarantula-dnn-gnn分级加速策略，从而提高定位效率。图1给出了本方法的具体流程，图2展示了本发明提出的分级加速策略。本发明概括来说主要包括以下步骤：
32.步骤1，使用包含至少一个失败用例的测试用例集测试包含缺陷的目标程序，并统计目标程序语句级以及函数级的频谱信息；并筛选出至少覆盖过一个失败错误用例的函数放入待排函数集m1；
33.步骤2，使用经典sbfl公式tarantula计算待排函数集m1中各函数的怀疑度分数，并将各函数按由tarantula计算得来的怀疑度分数从高到低进行排序，之后，选取排名前50的函数放入待排函数集m2以待进一步的排序；
34.步骤3，使用多种怀疑度计算公式计算函数集m2中各函数语句怀疑度分数，并组合成怀疑度向量，使用训练好的全连接神经网络(dnn)计算m2中各函数的怀疑度，并将各函数按由dnn计算来的怀疑度分数从高到低排序，之后，选取排名前10的函数放入待排函数集m3以待更精确的排序；
35.步骤4，对函数集m3中的所有函数进行静态分析，抽取各函数的控制流图和数据依赖图，并综合各函数内语句的怀疑度向量得到各函数的特征图；
36.步骤5，将步骤4得到的函数特征图两两输入到训练好的基于图神经网络的排序模型进行更精确的排序，得到程序函数的排序列表。至此，所有函数都已排序，按照此列表逐一检查直至排查到错误函数；
37.步骤6，当按步骤5得到的怀疑度列表检查至任意函数m时，将m的函数特征图输入到训练好的对边权重敏感的节点预测图神经网络进行二阶段错误定位，得到m中各语句按怀疑度大小由高到低排序的列表，通过此列表的提示来尽快定位到函数内缺陷语句。
38.以下部分就实施过程中的一些具体细节作更进一步的描述：
39.1.步骤2使用经典sbfl公式tarantula计算待排函数集m1中任意函数m的怀疑度分数，具体子步骤包括：使用tarantula公式计算函数m中各语句的怀疑度分数，对于语句s，给定其频谱(ef,e
p
,nf,n
p
)，使用tarantula计算语句s怀疑度的公式如下：
[0040][0041]
得到函数m内各语句的怀疑度后，取其中最大怀疑度作为函数m的怀疑度分数。
[0042][0043]
2.步骤3中使用怀疑度计算公式计算各语句的怀疑度向量，对函数集内的每一个函数m的每一条语句s，使用多个经典错误定位公式计算其怀疑度，并拼接成怀疑度向量vs。
[0044][0045]
其中，f为sbfl错误定位公式集，包括ochiai，tarantula，dstar，wong2，nashi1，nashi2，jaccard以及russellrao等。
[0046]
3.步骤4中对函数集m3内的每一个函数m，综合其控制流图g
cfg
、数据依赖图g
ddg
、m内各语句对应的怀疑度向量，获得函数的特征图其中，代表图g中所有的节点，在本发明中，图中每一个节点对应原函数中的一条语句，代表图中的关系类型(边种类)，在本发明中，关系类型分为控制流以及数据流。ε代表图中的所有边，为节点特征。图3为函数特征图示例。
[0047]
4.步骤5使用训练好的基于图神经网络的排序模型来比较任意两个函数的怀疑度大小，图4展示了此排序模型结构。该模型由图嵌入层和全连接层两部分组成，图嵌入层用来提取函数图的特征，全连接层来比较提取出的特征的怀疑度大小，输入为两个特征图g1和g2，输出结果代表g1和g2谁更可能是错误位置。图嵌入层计算公式如下：
[0048][0049][0050][0051][0052]
其中，代表节点u在第k次迭代时的隐藏值；代表以v节点为终点的所有邻居节点；其中wk为第k层神经网络的权重，总共有k层；σ代表激活函数，如relu，sigmoid；aggregate为聚合操作，可以为min，max或average；concat为拼接操作。在得到图g中各节点的嵌入表示后，通过readout操作获取图的嵌入表示。readout公示如下：
[0053][0054]
其中，d为节点特征维度，亦即所选用的怀疑度公式数量。在得到g1和g2的图嵌入表示h
g1
和h
g2
后，使用全连接神经网络(fc1)来比较g1和g2的怀疑度：
[0055]
p＝fc1(h
g1
,h
g2
)
[0056]
5.步骤6进行第二阶段错误定位得到函数内语句的怀疑度列表。图5为二阶段模型示意图。将函数特征图输入到训练好的节点预测图神经网络，得到各节点为缺陷节点的概率。其中，与一阶段的模型不同，二阶段模型考虑了函数图中各边的权重。边权重通过将边的频谱输入到一个训练好的神经网络得到，其中，边的频谱反映了该路径在执行过程中的
覆盖信息，与语句频谱类似，对于任一边e，其频谱也可表示为四元组(efe,epe,nfe,npe)。其中，efe代表了执行了该路径且执行失败的测试用例数，epe代表了执行了该路径且执行成功的测试用例数；nfe代表了没有执行该路径且执行失败的测试用例数，npe代表了没有执行该路径且执行成功的测试用例数。对于边e
ij
，只有当源节点i与目的节点j所代表的语句均被测试用例t覆盖时，我们才认为e
ij
被测试用例t覆盖。之后，将边频谱输入到训练好的全连接神经网络(fc2)得到该边的权重：
[0057]wij
＝fc2(ef
eij
,ep
eij
,nf
eij
,np
eij
)
[0058]
在得到各边的权重后，计算各节点的嵌入表示，节点嵌入计算公式如下：
[0059][0060][0061][0062][0063]
最后，使用全连接神经网络(fc3)计算各节点为错误节点的概率sv，公式如下：
[0064]