一种基于最优空间分解的乘积量化近邻检索方法

1.本发明涉及一种基于最优空间分解的乘积量化近邻检索方法，属于高维度数据检索领域。


背景技术：

2.近年来随互联网发展，高维度数据持续增长，数据检索压力巨大，尤其是如图像、文本数据一类的高维度数据检索。
3.pq算法(product quantization，也译为乘积量化)是图像检索中常用的一种快速搜索算法，pq算法将按顺序将原向量空间分解为若干个低维向量空间(如图2所示)的笛卡尔积，并对分解得到的低维向量空间分别进行量化处理。基于pq算法的近邻检索方法内存消耗低，且由于其较低的量化误差，检索精度高于基于哈希的近邻检索方法和基于树的近邻检索方法。但其检索精度仍然受到pq量化误差的影响。因此，需要一种检索精度更高的数据检索方法。


技术实现要素：

4.为了克服现有技术中存在的问题，本发明设计了一种基于最优空间分解的乘积量化近邻检索方法，将乘积量化的空间划分问题转化为一个使各子空间数据分布体积平衡的空间分解问题，实现了空间的合理划分，有效降低量化误差，提高检索精度。
5.为了实现上述目的，本发明采用如下技术方案：
6.一种基于最优空间分解的乘积量化近邻检索方法，包括以下步骤：
7.获取样本数据集；
8.求解样本数据集的空间分解最优解；
9.按空间分解最优解将样本数据集分解至m个子空间，并分别在各子空间内进行聚类分析，得到若干个簇；以簇质心为索引，构建倒排序表；
10.获取待检索数据；
11.按所述空间分解最优解将检待索数据分解至m个子空间，并分别在各子空间内检索若干个最接近簇；计算所述若干个最接近簇的笛卡尔积，得到若干个候选编码集；
12.根据所述多个候选编码集，查询倒排序表得到检索结果集。
13.进一步地，还包括：利用pca算法对样本数据进行降维处理。
14.进一步地，求解所述空间分解最优解，具体步骤为：
15.以分解后各子空间内数据维度的方差乘积平方根的累加值最小为目标，构建目标函数；求解所述目标函数，得到所述空间分解最优解。
16.进一步地，所述目标函数以公式表达为：
[0017][0018]
式中，表示第s子空间内数据维度的方差乘积平方
根；m表示子空间总数。
[0019]
进一步地，求解目标函数，包括如下步骤：
[0020]
a1、选取样本数据集中方差第t大和方差第t小的维度分配至srvp值最小的子空间并更新该子空间的srvp值，直至该子空间内维度数量等于d/m；
[0021]
a2、重复步骤a1，直至所有维度都被分配至子空间。
[0022]
进一步地，还包括：根据量化误差，设置各子空间的最接近簇数量。
[0023]
进一步地，所述子空间的量化误差越小，该子空间的最接近簇数量越多。
[0024]
进一步地，所述设置各子空间的最接近簇数量，具体步骤为：
[0025]
预设一最接近簇总数z；
[0026]
根据量化误差占比对各子空间进行排序；
[0027]
根据未确定最接近簇数量值的子空间数量和最接近簇总数z，计算该子空间的最接近簇数量值；根据计算得到的最接近簇数量值，更新z值；按排序结果，顺序计算下一子空间的最接近簇数量值并更新z值，直至得到所有子空间的最接近簇数量值。
[0028]
进一步地，还包括：
[0029]
计算某一子空间的量化误差占比；根据所述量化误差占比，计算该子空间的权重值；根据所述权重值，调整该子空间的最接近簇数量值。
[0030]
进一步地，所述计算子空间最接近簇数量，以公式表达为：
[0031][0032][0033]
式中，rs表示第s子空间的最接近簇数量；floor()表示向下取整函数； ceil()表示向上取整函数；ps表示第s子空间的量化误差占比；z表示最接近簇总数；m-i表示未确定最接近簇数量值的子空间数量；m表示子空间总数。
[0034]
与现有技术相比本发明有以下特点和有益效果：
[0035]
1、现有pq算法中采用顺序空间分解，量化误差较大。而本发明将其转化为一个使各子空间数据分布体积平衡的空间分解问题并利用方差衡量各维度的长度，从而构建如式(2)所示的便于求解的目标函数，通过求解目标函数实现空间的合理分解，有效降低量化误差，提高检索精度。
[0036]
2、本发明技术人员考虑到：不同的子空间具有不同的量化误差，量化误差小则意味着数据分布范围紧凑，其聚类半径更小。因此，在量化误差比较小的子空间需要检索更多族群才能包含近邻点；而在量化误差较大的子空间只需要检索较少族群就能包含近邻点。故，本发明利用量化误差设置各子空间的最接近簇数量并使量化误差越小的子空间，分配的最接近簇数量越多，有利于获得质量更高的检索结果集，从而提高检索精度。
附图说明
[0037]
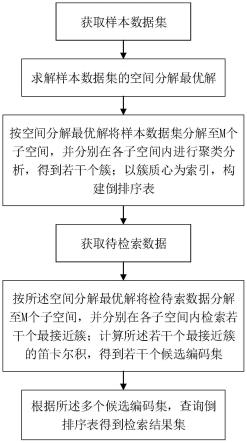
图1是本发明流程图；
[0038]
图2是现有技术示意图；
[0039]
图3是本发明所示最优空间分解示意图；
[0040]
图4是实施例三实验结果示意图。
具体实施方式
[0041]
下面结合实施例对本发明进行更详细的描述。
[0042]
实施例一
[0043]
如图1所示，一种基于最优空间分解的乘积量化近邻检索方法，包括以下步骤：
[0044]
s1、构建样本数据集：
[0045]
获取n张图片；提取每一图片的特征向量，特征向量集即为样本数据集
[0046]
s2、通过pca算法对样本数据集作降维处理：
[0047]
对样本数据集x的每一行进行零均值化；计算x的协方差矩阵；计算协方差矩阵的特征值及对应的特征向量；将特征向量按对应特征值大小从上到下按行排列成矩阵，取前d行组成矩阵a；x
′
＝ax，x
′
即降至d维后的样本数据集。
[0048]
s3、求解样本数据集的空间分解最优解：
[0049]
计算样本数据集x
′
中每一维度的方差σ＝[σ
(1)
,σ
(2)
,
…
,σ
(d)
]，且经pca算法降维得到样本数据集x
′
中σ
(1)
》σ
(2)
》
…
》σ
(d)
；
[0050]
为使子空间数据分布尽可能平衡，从而保证乘积量化误差最小，以划分后子空间数据分布体积累加值最小为目标，构建目标函数如式(1)：.
[0051][0052][0053]
式中，v(xs′
)表示子空间xs′
的数据分布体积，b表示数据分布的半径。约束条件为：各子空间互不相交；样本数据集x
′
的所有维度都包含在子空间的并集中。
[0054]
定义d个维度的方差乘积平方根
[0055]
本实施例中用方差衡量各维度的长度，并假设数据分布是均匀分布，其方差δ＝(b-a)(本实施例中预先假设a＝0，b即数据分布的长度)。显然，即srvp＝12
d/2
v.由于12
d/2
只是一个常数，因此将式子(1) 表示为式(2)：
[0056][0057][0058]
式中，表示子空间内数据x
′s维度的方差乘积平方根。
[0059]
基于贪心思想，利用表1所示算法求解式(2)的最优解，算法执行如下过程：
[0060]
首先为m个子空间定义m个空集列表，列表与子空间一一对应；执行多次循环，每次
循环选取样本数据集中第t维度和第(d+1-t)维度放入srvp值最小的子空间内(s《m)，执行结果如图3所示。本实施例中σ
(1)
》σ
(2)
》
…
》 σ
(d)
，则第t维度和第(d+1-t)维度即为方差第t大和方差第t小的维度。比如说 d＝8，m＝2，分解结果为[1、8、2、7]，[3、6、4、5]。
[0061][0062]
s4、按步骤s3求得的空间分解最优解，将样本数据集x
′
分解至m个子空间，并在各子空间内进行聚类分析，得到若干个簇；以簇质心为索引，构建倒排序表it(code)＝{x:x∈x and code＝idx(x)}。
[0063]
s6、获取检待索数据，并通过pca算法将待检索数据降至d维；
[0064]
s7、按所述空间分解最优解将d维的检待索数据分解至m个子空间，得到 q
′
＝(q
′1,q
′2,
…
,
′m)；在各子空间内检索r个最接近簇；计算所述若干个最接近簇的笛卡尔积，得到包含rm个候选编码集。如，对第s子空间，其检索得到的 r个最接近簇的簇质心为：
[0065]
其最终得到的候选编码集为
[0066]
且|candidate_index|＝rm。
[0067]
根据所述rm个候选编码集，查询倒排序表，命中目标组成检索结果集。
[0068]
实施例二
[0069]
本实施例与实施例一的不同之处在于，根据量化误差为各子空间设置不同的最接近簇数量[r1,
…
,s,
…
,rm]，具体步骤为：
[0070]
根据子空间的量化误差,计算其量化误差占比ps，见式(3)：
[0071][0072]
式中，errs表示第s子空间的量化误差。
[0073]
定义第s子空间的最接近簇数量rs，如式(4)
[0074][0075]
利用表2所示算法求解式(4)，算法执行如下过程：
[0076]
预先设置一最接近簇总数z；计算子空间的权重值将各子空间按量化误差由大至小进行排序；
[0077]
首先根据未处理的子空间数量，从z中为本次计算的子空间分配一初始簇数δr；将作为其权重与δr相乘即得到该子空间的最接近簇数量值；动态更新z，即从z中除去此次计算的最接近簇数量值；按排序结果，顺序计算下一子空间的最接近簇数量，直至得到所有子空间的最接近簇数量值。
[0078][0079]
显然，量化误差越小的子空间，按上述过程计算所得的值和δr值越大，分配到的rs越大(errs越小，子空间顺序越靠后即m-i值越小；m-i值越小，值越大)。
[0080]
经上述过程得到[r1,
…
,rm]。则对q
′
＝(q
′1,q
′2,
…
,q
′m)，前rs个离q
′s最近的簇索引则候选编码集且且最终，检索结果集candidates＝{it(idx)|idx∈candidate_imdex}。
[0081]
本发明技术人员考虑到不同的子空间具有不同的量化误差.量化误差小则意味着数据分布范围紧凑，其聚类半径更小。因此，在量化误差比较小的子空间需要检索更多族群才能包含近邻点；而在量化误差较大的子空间只需要检索较少族群就能包含近邻点。本发明利用量化误差设置各子空间的最接近簇数量且使量化误差越小的子空间，分配的最接近簇数量越多，有利于获得质量更高的检索结果集，从而提高检索精度。
[0082]
实施例三
[0083]
在此处先进行名词解释：
[0084]
osdpq-本发明实施例一所述基于最优空间分解方法的乘积量化近邻检索方法
[0085]
pq-乘积量化算法(product quantization)
[0086]
opq-优化乘积量化算法(optimized product quantization)
[0087]
opq(p)-优化乘积量化算法(参数版本)
[0088]
opq(np)-优化乘积量化算法(无参数版本)，@number表示迭代次数
[0089]
rvq-残差矢量量化算法(residual vector quantization,rvq)
[0090]
lti-learning to index for nearest neighbor
[0091]
本实施例使用三个数据集进行近似近邻检索实验，三个数据集如表3所示。
[0092]
表3
[0093][0094][0095]
通过对比不同算法在检索结果数量相同情况下的k近邻精度，来衡量算法检索精度。k近邻精度的计算方法见下式。
[0096][0097]
其中，ak＝{a1,a2,
…
,ak}表示待检索数据q的实际k近邻元素集。top k
‑ꢀ
recall表示检索结果集中的k近邻占实际k近邻元素的比例。
[0098]
1、量化误差对比
[0099]
表4展示了三个数据集经osdpq、(opq(p))和(opq(np))进行空间分解的量化误差。总体上看，在迭代次数足够的情况下，opq(np)具有最小的量化误差，而osdpq的量化误差在三个数据集上均小于pq和opq(p)。
[0100]
表4
[0101] mnistgist1msift1mpq2.395
×
1058.30
×
1021.652
×
105opq(p)2.234
×
1057.69
×
1021.578
×
105opq(np)@502.063
×
1057.54
×
1021.554
×
105opq(np)@1002.049
×
1057.48
×
1021.539
×
105opq(np)@1502.051
×
1057.43
×
1021.478
×
105opq(np)@2002.052
×
1057.34
×
1021.477
×
105osdpq2.205
×
1057.39
×
10
25
1.572
×
105[0102]
pq、opq(p)和osdpq利用固定的步骤对数据维度进行分解，而opq(np) 则通过多次迭代，并在迭代过程中通过旋转和投影不断调整数据的变换矩阵，改变数据的分布，以期获得最小的量化误差。由于数据分布的多样性，单纯在量化误差上opq(np)具有更好的表现，但是其迭代过程导致算法效率低下，降低了可用性。
[0103]
2、检索精度对比与分析
[0104]
osdpq与pq、opq、rvq、lti方法的检索精度对比如图4所示。图4 展示了各算法检索精度与检索结果数量之间的关系曲线(top1表示检索结果数量为1个，top10表示检索结果数量为10个)。从图中可以看出，检索精度随着检索结果数量的增加而提高。为了叙述方便，+表示本文方法精度优于对比方法，反之用-表示。
[0105]
在gist1m数据集中，osdpq展现出了最高的检索精度，opq(p)次之。在检索结果数量为2000个的时候，osdpq比opq(p)、opq(np)@200、pq、 rvq和lti在top1和top10上分别提高(+1.10％,+2.94％),(+1.7％, +4.2％),(+20.25％,+25.05％),(+6.05％,+6.89％)和(+5.62％,+4.63％)(如图4(a,b) 所示)。显然，(1)pq的检索精度远远落后于osdpq、opq(p)和opq(np)；(2) opq(np)@200取得了最低量化误差(如表4所示)，但其检索精度却非最高。
[0106]
出现现象(1)的原因是gist1m数据分布极其不均衡，在不考虑任何先验知识的情况下，pq的顺序空间分解会导致各子空间数据体积极其不平衡，严重降低pq的检索精度。出现现象(2)的原因则可能是数据集分布的多样性，而 opq(np)@200过度追求量化误差最小化，从而导致倒排序表数据分布的不均衡所致。
[0107]
在sift1m数据集中，osdpq随着检索结果的增加逐渐展现出很好的检索精度。在检索结果数量小于1600时，opq(np))@200取得了最优的检索精度；在检索结果数量为1600个的时候，osdpq与opq(p)、opq(np)@50、 opq(np)@100、opq(np)@150、opq(np)@200、pq、rvq和lti在top1上分别相差+1.98％,+4.70％,+1.44％,-1.21％,-1.75％,+5.15％,+3.40％和+4.80％(如图4(c)所示)。随着检索结果数量的增加，osdpq与最优方法opq(np)@200 的差距不断减少(如图4(c,d)所示)。在检索结果数量为1800个的时候， osdpq在top1上比opq(np)@200低1.20％；而在检索结果数量为2000个的时候，osdpq仅比opq(np)@200低0.3％。
[0108]
在mnist数据集中，osdpq总体上展现出较好的检索精度。在检索结果数量为800
时，osdpq与pq、opq(p)、opq(np)@50、opq(np)@100、 opq(np)@150、opq(np)@200、rvq和lti在进行top1和top10查询时分别相差(+13.40％,+6.96％)、(+3.36％,+0.85％)、(+3.60％,+0.60％)、(+1.66％,
‑ꢀ
1.00％)、(-0.56％,-1.30％)、(+1.18％,-1.81％)、(+8.96％,+2.60％)和(+17.81％, +14.49％)(如图4(e,f)所示)。由于mnist数据各主成分分布较均衡(如fig3所示)，pq的空间分解方式得到各子空间数据分布体积也相对均衡，因此pq与 osdpq、opq(p)和opq(np)在相同检索结果数量的情况下的检索精度差异较小。而在相同情况下，gist1m数据集上则展现出更大的精度差异。
[0109]
3、构建索引时间和内存消耗对比
[0110]
在osdpq与opq(np)检索精度相近的情况下(sift1m:opq(np)@80； gist1m:opq(np)@200；mnist:opq(np)@100)，osdpq和opq(np)索引结构构建的时间分别为:(581.23s,2421.86s)、(664.85s,10230.12s)和(15.17s,155.42s)。在这三个数据集上，osdpq的构建效率分别比opq提升了4.17倍，15.83倍和10.24倍。
[0111]
在sift1m、gist1m和mnist数据集上，osdpq和opq(np)所消耗的内存分别为(2832.81mb,3194.35mb)；(3656.56mb,4075.66mb)；
[0112]
(1577.93mb,2017.58mb)。osdpq在三个数据集上内存消耗分别比opq降低了 11.3％、10.3％和21.8％。
[0113]
综上，本发明实施例一所述基于最优空间分解方法的乘积量化近邻检索方法(osdpq)相比现有技术能有效降低量化误差，提高检索精度；同时消耗更少的时间和内存，实时性强。
[0114]
实施例四
[0115]
drqe-本发明实施例二所述基于量化误差设置各子空间的最接近簇数量的方法。将drqe应用于pq，opq(p)和opq(np)，drqe对各算法检索精度的影响如表5所示。
[0116]
表5
[0117][0118]
在mnist数据集上，pq、opq(p)、opq(np)@200和osdpq的检索精度在top-1和top-10查询上分别提高(5.96％,4.28％)、(0.78％,1.25％)、(1.67％, 0.46％)和(1.64％,1.11％)。
[0119]
在sift1m数据集中,pq、opq(p)、opq(np)@200和osdpq的检索精度在 top-1和top-10查询上分别提高(3.95％,2.92％)、(1.30％,1.04％)、(2.00％, 2.15％)和(0.45％,2.04％)。
[0120]
在gist1m数据集中,pq、opq(p)、opq(np)@200和osdpq的检索精度在 top-1和top-10查询上分别提高(3.10％,2.35％)、(2.30％,1.30％)、(2.05％, 2.98％)和(1.85％,1.95％)。
[0121]
综上，本发明实施例二所述基于量化误差设置各子空间的最接近簇数量的方法广泛适用于各类基于乘积量化的近邻检索方法，且能有效提高检索精度。
[0122]
显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。