基于EFA-BBN的计算机量化预测人员失误概率的方法和系统

基于efa-bbn的计算机量化预测人员失误概率的方法和系统
技术领域
1.本发明涉及数据分析与计算机预测技术领域，具体涉及一种基于efa-bbn的计算机量化预测人员失误概率的方法和系统。


背景技术：

2.确定影响人员失误的行为形成因子(psfs)是人员可靠性分析(hra)工作中的关键步骤之一。现有研究成果中提出了针对psfs的结构层次分类法，目的是减少psf之间的重叠性，并通过建模、观察和专家判断来进一步探索它们的因果关系。这些研究成功推进了对psfs相关性的研究，然而，它们是在强烈依赖专家判断的前提下，并且只限于确定两个或三个因素之间的因果关系。此外，psfs的重叠性和因果关系是通过传统技术来研究的，这些技术没有考虑到psfs之间关系的不确定性。
3.目前，在分析人员失误概率(human error probabilities,heps)时，一些方法只考虑一个psf，如时间可靠性方法，另一些方法已经考虑了多达50个psfs，如idac。只考虑少数几个psfs可以简化分析工作量，但可能无法完整描述人员失误原因，而考虑大量psfs会引入psfs相关性的不确定性并增加工作负担。由于现有的方法通常忽略了行为形成因子(psfs)间的关系，从而导致人员失误概率(hep)的预测结果存在一定的误差。


技术实现要素：

4.本发明目的之一是提供一种基于efa-bbn的计算机量化预测人员失误概率的方法，用以更准确地预测人员失误概率。
5.为了实现上述目的，本发明采用的基于efa-bbn的计算机量化预测人员失误概率的方法包括以下步骤：
6.一、生成当前情境条件下的efa-bbn模型；
7.以通用bbn模型为基础，所述通用bbn模型结构为：以多种情境下影响人员失误的psfs作为父节点，以人员失误概率作为子节点，以psfs聚类分析得到的聚类因子作为连接父节点和子节点的中间节点；
8.利用efa法结合当前情境条件对通用bbn模型中的psfs进行分析，生成psf对聚类因子贡献权重值的均匀分布，以对聚类因子贡献权重值大于0.5为筛选标准，对于满足该标准的psfs，保留其与中间节点的关系，对于不满足该标准的psfs，则删除其与中间节点的关系，生成当前情境条件下的efa-bbn模型；
9.二、efa-bbn模型的量化；
10.从存储有多种情境下影响人员失误的psfs及其条件概率分布数据的数据库中获取模型中保留的psfs的条件概率并将概率值归一化，再基于与父节点状态相关的聚类因子的概率密度函数获得中间节点的条件概率，以及利用成功似然指数法估算子节点，得出当前情境条件下人员失误概率的量化预测结果。
11.于本发明一实施例中，上述方法还包括构建通用bbn模型的步骤：
12.从所述数据库中获取多种情境下影响人员失误的psfs并将其作为父节点，以人员失误概率作为子节点，对获取的psfs进行聚类分析，以聚类因子作为连接父节点和子节点的中间节点，得到通用bbn模型。
13.在步骤一中，利用efa法结合当前情境条件对通用bbn模型中的psfs进行分析的过程包括：
14.(1)当psf i在当前情境条件下发生时，赋值为1，如若不可能发生，则赋值为0；
15.(2)将通用bbn模型中的n个psf的赋值输入spss软件进行efa分析，产生m个聚类因子，以ω
ij
表示psf i对聚类因子j的贡献权重值，用ω
base
(i，j)表示psf i对聚类因子j的贡献权重基准值，且i＝1，2，...，n，j＝1，2，...，m；
16.(3)将所有的psfs分为a和b两组，a组仅包含psf在当前情境条件下发生的情况，b组仅包含psf在当前情境条件下不发生的情况；对两组中的psf分别用spss进行分析，在每次spss运行中预先设定m个聚类因子，a、b两组中psf经efa分析得到的结果分别为ω
psf i＝1
(i，j)和ω
psf i＝0
(i，j)；
17.(4)从ω
psf i＝0
(i，j)和ω
psf i＝1
(i，j)中确定最小值ω
min
(i，j)和最大值ω
max
(i，j)，令然后设置a
ij
＝ω
base
(i，j)-d
ij
，b
ij
＝ω
base
(i，j)+d
ij
，生成psf i对聚类因子j贡献权重值ω
ij
的均匀分布u(a
ij
，b
ij
)；
18.之后，从u(a
ij
，b
ij
)获取psf i的ω
ij
值，若ω
ij
＞0.5，则该psf i与聚类因子j的关系保留，否则删除。
19.在步骤二中，基于与父节点状态相关的聚类因子的概率密度函数获得中间节点的条件概率的过程包括：
20.定义tnj(μj，σ
j2
，0，1)为聚类因子j的概率密度函数，其中，μj是psfs的加权函数，σj是标准偏差，σ
j2
为方差，截断区间是[0，1]；
[0021]
μj的值通过以下式(1)确定：
[0022][0023]
式(1)中，i∈n，p(psfi)是psf i的先验概率，ω
ij
是psf i对聚类因子j的贡献权重；
[0024]
在区间[0，1]上对tnj进行离散化，得到中间节点的条件概率
[0025]
于本发明一实施例中，步骤二中利用成功似然指数法估算子节点的基本公式为：
[0026]
log(hep)＝a
·
sli+b
ꢀꢀꢀ
(2)；
[0027]
式(2)中，a和b是常数，sli为某个操作任务的成功可能性指数：
[0028][0029]
式(3)中，wj是聚类因子j归一化权重，作为衡量其对相应操作任务的影响程度所有聚类因子j都取相等的权重，rj是聚类因子j在多大程度上发生在某项任务中，其值取1到9中的整数值；
[0030]
由式(3)获得的9m个sli值位于区间[1，9]中；将区间[1，9]分成k个相等的部分：i1、
i2……
ik，k为聚类因子j的状态种类数；将9m个sli值分配至k个区间，计算k个平均值：
[0031]
基于式(2)和上述k个平均值得到中，s＝i1、i2……
ik；
[0032]
基于与聚类因子相关的sli节点的概率密度函数获得sli节点的条件概率
[0033]
最后，利用下式计算得到当前情境条件下人员失误概率的量化预测结果：
[0034][0035]
式(4)中，p(hep＝yes)表示人员失误概率。
[0036]
进一步地，tnj(μj，σ
j2
，0，1)中，方差σ
j2
值设置为2
×
10-2
。
[0037]
于本发明一实施例中，式(2)中的a和b的值分别设置为-0.348和0.128。
[0038]
于本发明一实施例中，聚类因子j包括低、中、高三种状态，区间[1，9]被分成三个相等的部分：i1＝[1，3.67)、i2＝[3.67.6.34)、i3＝[6.34，9]，将9m个sli值分配至三个区间，计算三个平均值：间，计算三个平均值：和
[0039]
并基于式(2)和三个平均值和得到中，s＝i1、i2、i3。
[0040]
另外，本发明还涉及一种基于efa-bbn的计算机量化预测人员失误概率的系统，其包括：
[0041]
数据库，存储有多种情境下影响人员失误的psfs及其条件概率分布数据；
[0042]
efa-bbn模型生成模块，用以从所述数据库中获取多种情境下影响人员失误的psfs并将其作为父节点，以人员失误概率作为子节点，对获取的psfs进行聚类分析，以聚类因子作为连接父节点和子节点的中间节点，构建通用bbn模型；以及，利用efa法结合当前情境条件对通用bbn模型中的psfs进行分析，生成psf对聚类因子贡献权重值的均匀分布，以对聚类因子贡献权重值大于0.5为筛选标准，对于满足该标准的psfs，保留其与中间节点的关系，对于不满足该标准的psfs，则删除其与中间节点的关系，生成当前情境条件下的efa-bbn模型；
[0043]
计算模块，用以从数据库中获取当前情境条件下的efa-bbn模型中保留的psfs的条件概率并将概率值归一化，再基于与父节点状态相关的聚类因子的概率密度函数获得中间节点的条件概率，以及利用成功似然指数法估算子节点，计算得出当前情境条件下人员失误概率的量化预测结果。
[0044]
于本发明另一实施例中，基于efa-bbn的计算机量化预测人员失误概率的系统包括：
[0045]
数据库，存储有多种情境下影响人员失误的psfs及其条件概率分布数据；
[0046]
存储器，存储有通用bbn模型，所述通用bbn模型是以多种情境下影响人员失误的psfs作为父节点，以人员失误概率作为子节点，以psfs聚类分析得到的聚类因子作为连接父节点和子节点的中间节点；
[0047]
efa-bbn模型生成模块，从存储器中调用通用bbn模型并利用efa法结合当前情境条件对通用bbn模型中的psfs进行分析，生成psf对聚类因子贡献权重值的均匀分布，以对
聚类因子贡献权重值大于0.5为筛选标准，对于满足该标准的psfs，保留其与中间节点的关系，对于不满足该标准的psfs，则删除其与中间节点的关系，生成当前情境条件下的efa-bbn模型；
[0048]
计算模块，用以从数据库中获取当前情境条件下的efa-bbn模型中保留的psfs的条件概率并将概率值归一化，再基于与父节点状态相关的聚类因子的概率密度函数获得中间节点的条件概率，以及利用成功似然指数法估算子节点，计算得出当前情境条件下人员失误概率的量化预测结果。
[0049]
与现有技术相比，本发明利用efa法结合当前情境条件对bbn模型中的父节点psf进行分析，并将psf相关性聚类为中间因子，连接bbn模型的父节点和子节点，该预测方法对psf的数量没有限制，可以将n个psfs聚类成少量中间因子，而不会失去psf原本信息的完整性，所生成的efa-bbn模型可以弥补现有hra方法没有考虑psfs间的关系这一缺陷，并且模型中聚类因子节点和子节点均基于双重截断正态分布(tn)来获取条件概率表，然后利用成功似然指数(slim)方法估计人员失误概率值，相较于现有的hra方法，本发明能够减少专家判断的主观性，更准确地估算出人员失误概率。
附图说明
[0050]
图1是通用bbn模型的结构示意图；
[0051]
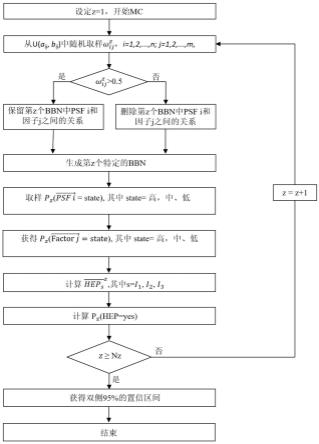
图2是蒙特卡洛随机抽样过程的流程图；
[0052]
图3是对89份人因事件报告进行分析所得到的八个psf对人为错误事件的贡献百分比图；
[0053]
图4为按照图2中的流程执行100次蒙特卡洛随机抽样，所得到的人员失误概率值曲线图；
[0054]
图5-7分别为案例1～3中基于bbn的slim模型。
具体实施方式
[0055]
为了便于本领域技术人员更好地理解本发明相对于现有技术的改进之处，下面结合附图和实施例对本发明作进一步的说明。本发明的实施例中主要包括两大部分内容，第一部分主要介绍efa-bbn模型的构建及量化，第二部分主要是案例的分析说明以及模型验证的结果，接下来分别对以上两部分的内容进行详细介绍。
[0056]
一、efa-bbn模型的构建及量化
[0057]
1.1.基于探索性因子分析(efa)法构建贝叶斯模型(bbn)
[0058]
在核电厂中，操纵员在不同情境下执行任务，影响人员失误的行为形成因子(psfs)及其相关关系在不同情境下的表现形式存在差异。基于此，在如图1所示考虑n个psfs的通用bbn模型的基础上，根据efa技术，建立具体情境下的efa-bbn模型。
[0059]
efa法能够将高度相关的多个变量结合起来，通过聚类因子来揭示变量的相互关系。利用efa法结合具体情境条件对通用bbn模型中的psfs进行分析：
[0060]
(1)当psf i在该情境条件下发生时，赋值为1，如若不发生，则赋值为0。
[0061]
(2)将通用bbn模型中的n个psf的赋值输入spss软件进行efa分析，产生m个聚类因子，以ω
ij
表示psf i对聚类因子j的贡献权重值，用ω
base
(i，j)表示psf i对聚类因子j的贡
献权重基准值，且i＝1，2，...，n，j＝1，2，...m。
[0062]
(3)将所有的psfs分为a和b两组，a组仅包含psf在该情境条件下发生的情况，b组仅包含psf在该情境条件下不发生的情况；对两组中的psf分别用spss进行分析，在每次spss运行中预先设定m个聚类因子，a、b两组中psf经efa分析得到的结果分别为ω
psf i＝1
(i，j)和ω
psf i＝0
(i，j)。
[0063]
(4)从ω
psf i＝0
(i，j)和ω
psf i＝1
(i，j)中确定最小值ω
min
(i，j)和最大值ω
max
(i，j)，令然后设置a
ij
＝ω
base
(i，j)-d
ij
，b
ij
＝ω
base
(i，j)+d
ij
，生成psf i对聚类因子j贡献权重值ω
ij
的均匀分布u(a
ij
，b
ij
)。
[0064]
之后，从u(a
ij
，b
ij
)获取psf i的ω
ij
值，efa中定义了一个标准，本发明选择遵守efa标准，只有当ω
ij
＞0.5时，考虑psfs之间的相关关系；否则不考虑，即若ω
ij
＞0.5，则该psf i与聚类因子j的关系保留，否则删除。
[0065]
1.2.efa-bbn模型的量化
[0066]
在efa-bbn模型中，中间节点和子节点(即聚类因子节点和hep节点)通过双重截断正态分布(tn)来获取cpts(条件概率)，然后，集成成功似然指数(slim)方法估计heps。
[0067]
1.2.1.cpt的获取
[0068]
在本实施例中，tnj(μj，σ
j2
，0，1)被定义为聚类因子j的概率密度函数，它取决于与其高度相关的psfs，μj是psfs的加权函数，σj是标准偏差，截断区间是[0，1]。
[0069]
在不丧失一般性情况下，采用下式(1)来确定μj的值，即：
[0070][0071]
式中，i∈n，p(psfi)是psfi的先验概率，ω
ij
是psf i对因子j的贡献权重，方差σ
j2
设置为2
×
10-2
。
[0072]
在区间[0，1]上对tnj进行离散化，即可得到中间节点的条件概率定义聚类因子j有低、中、高三种状态，则在区间[o，1]上对tnj进行离散化，则将得到p(factor j＝低)，p(factor j＝中)，和p(factor j＝高)。
[0073]
1.2.2.hep的估算
[0074]
采用slim方法来估算hep，该方法是较为广泛认可的人员可靠性分析方法，基本公式为：
[0075]
log(hep)＝a
·
sli+b
ꢀꢀꢀ
(2)；
[0076]
上式中，a和b是常数，本实施例中，分别设置为-0.348和0.128。sli是某个操作任务的成功可能性指数：
[0077][0078]
其中，wj是聚类因素j归一化权重。作为衡量其对特定任务的影响程度这里对所有因素j都取相等的权重，即w1＝
…
＝wj＝
…
＝w
m，
，主要有两个原因：(i)聚类因子j用于连接psf节点和hep节点，起结构作用；(ii)聚类因子j已经以权重ω
ij
考虑了psf对人员绩效的影响。rj是聚类因子j在多大程度上发生在某项任务中，其值取1到
9中的整数值。
[0079]
由于wj是相等的值，rj取一个从1到9的整数值，因此，根据式(3)可以获得9m个sli值(有多个相同的sli值)位于区间[1，9]中。根据聚类因子j的状态种类数将区间[1，9]等分，例如聚类因子j包括k中状态，则将区间[1，9]分成k个相等的部分。在本实施例中，由于聚类因子j包括低、中、高三种状态，故将区间[1，9]分成三个相等的部分：i1＝[1，3.67)，i2＝[3.67，6.34)，i3＝[6.34，9]。然后，将9m个sli值分配给三个区间，计算三个区间中sli的平均值：平均值：
[0080]
基于公式(2)和三个平均值和可以得到：和
[0081]
然后，采用1.2.1中同样的方法来获取hep节点的cpt。对于三个区间i1、i2和i3，获得sli节点的条件概率为定义sli有低、中、高三种状态，则得到p(sli＝low)，p(sli＝medium)和p(sli＝high)。
[0082]
由于hep节点只有sli节点作为输入节点，那么，hep节点的cpt可以由下式(4)和(5)计算：
[0083][0084]
p(hep＝no)＝1-p(hep＝yes)
ꢀꢀꢀ
(5)；
[0085]
其中p(hep＝yes)是发生人员失误的概率，其中，式(4)可表示为：
[0086]
1.2.3.蒙特卡洛随机抽样
[0087]
基于以上过程，构建一种蒙特卡洛(mc)抽样法来计算heps的置信区间，在计算机上进行mc抽样过程见图2所示，包括以下步骤：
[0088]
在第z次mc时，z＝1，2，...，nz：
[0089]
(1)从u(a
ij
，b
ij
)中随机抽样如果则保留从psf i到聚类因子j的关系，并将聚类因子的个数记为mz。
[0090]
(2)生成第z个bbn模型。
[0091]
(3)从保留的psf i的概率分布中取样并将概率值归一化其中state＝高，中、低。
[0092]
(4)输入和σ2到agenarisk软件中获取其中state＝高，中、低。
[0093]
(5)输入获取其中state＝高，中、低。
[0094]
(6)基于mz，其中s＝i1、i2、i3。
[0095]
(7)计算其中s＝i1、i2、i3，state＝高，中、低。
[0096]
重复步骤(1)到(7)nz次，得到p(hep＝yes)的双侧95％置信区间。
[0097]
二、案例分析和验证结果
[0098]
2.1.案例分析
[0099]
以文献“gertman d，blackman h，marble j，byers j，smith c.the spar-h human reliability analysis method.nureg/cr-6883.washington，dc：u.s.nuclear regulatory commission；2005”的spar-h方法中的8个psfs(可用时间、压力/压力源、复杂度、经验/培训、规程、人因工程/人机界面、职责适宜、工作过程)为对象，分析它们的相关关系。从国家核安全局经验反馈平台中，收集了89份人因事件报告，涉及不同类型的反应堆，包括cnp300、cnp600、candu、m310、cpr1000、vver等。对这89份人为错误事件报告进行了分析，结果如图3所示，该结果与文献“park j，jung w，kim j.inter-relationships between performance shaping factors for human reliability analysis of nuclear power plants.nuclear engineering and technology 2020；52(1)：87-100”中的结果一致。
[0100]
由图3可知，工作过程对57.3％的事件有影响，是最频繁发生的psf，工作过程是指流程设计方面的psf，不适当的流程可能导致人为错误的因素。另外，只有2.2％的人因事件和职责适宜psf有关，是记录最少的psf，该现象说明人员失误很少是由职责适宜引起。
[0101]
将89份报告的分析结果输入spss软件中执行efa分析，ω
base
(i，j)结果如表1所示。按标准ω
ij
＞0.5，复杂度(ω
base
(1，1)＝0.76)、可用时间(ω
base
(5，1)＝0.61)、压力/压力源(ω
base
(6，1)＝0.84)和职责适宜(ω
base
(8，1)＝0.72)聚类为因素1。规程(ω
base
(2，2)＝0.69)、人因工程/人机界面(ω
base
(3，2)＝0.71)、经验/培训(ω
base
(4，2)＝0.53)和工作过程(ω
base
(7，2)＝0.69)聚类为因素2。此外，规程对因素3的贡献ω
base
(2，3)为0.5，这里不考虑因子权重位于标准边界时的情况。
[0102]
表1 8个psf对3个聚类因素的贡献权重
[0103][0104]
单元格中的权重值是绝对值。
[0105]
考虑ω
base
(i，j)值的不确定性，针对8个psf，将每一个psf的数据分成两组(psf i＝1和psf i＝0)。用spss对16组数据集进行分析，均提前设置3个聚类因子。因此efa分析产生16组权重值。在此基础上，找到ω
min
(i，j)和ω
max
(i，j)并生成ω
ij
的均匀分布，结果如表2所示。
[0106]
表2 psf对三个聚类因素的贡献权重分布
[0107][0108]
psfs(即父节点)的条件概率分布如表3所示，各psfs(即父节点)的条件概率分布均为已知数据。
[0109]
表3 psf状态的概率分布
[0110]
[0111]
2.2.结果
[0112]
按照图2中的mc过程，执行100次，得到100个p(hep＝yes)值，如图4所示。p(hep＝yes)的平均值为3.7e-2，与spar-h方法提供的诊断hep的数量级一致。本实施例基于加权平均函数和mc取样所得的heps，反映了人员失误概率的一般特征的置信度，并且处在基准hep范围内(1.0e-5，1)。
[0113]
专家判断法广泛用于hra中hep的估计，但是，它会导致主观性和不确定性，本实施例中p(hep＝yes)的双侧95％置信区间为[2.75e-02，4.66e-02]，可以增加hep估计的置信度，减少主观性。
[0114]
图5-7示出了三个不同案例下的基于bbn的slim模型。
[0115]
图5(案例1)中，复杂度(ω
11
＝0.76)、可用时间(ω
51
＝0.61)、压力/压力源(ω
61
＝0.84)和职责适宜(ω
g1
＝0.72)贡献于因素1，而规程(ω
22
＝0.69)、人因工程/人机界面(ω
22
＝0.71)、经验/培训(ω
42
＝0.53)和工作过程(ω
72
＝0.69)贡献于因素2。贡献因素1的psfs与人的心理有关，贡献因素2的psfs更多地反映了系统情况。
[0116]
图6(案例2)中，复杂度(ω
11
＝0.62)、经验/培训((ω
41
＝0.53)、可用时间(ω
51
＝0.56)、压力/压力源(ω
61
＝0.73)、职责适宜(ω
g1
＝0.59)贡献因素1，而人因工程/人机界面(ω
32
＝0.95)和工作过程(ω
72
＝0.87)贡献因素2。规程psf没有在本案例中发生，这说明规程psf并不总是与其他psf相互作用来影响人员绩效。与案例1相比，经验/培训与人的心理因素相互作用，而不与系统情境因素相互作用。这意味着经验/培训是影响系统和人的心理的中介因素。
[0117]
图7(案例3)中，复杂度(ω
11
＝0.75)、经验/培训(ω
41
＝0.581)、压力/压力源(ω
61
＝0.848)、工作过程(ω
71
＝0.787)和职责适宜(ω
g1
＝0.904)贡献因素1，规程(ω
22
＝0.524)、人因工程/人机界面(ω
32
＝0.581)、经验/培训(ω
42
＝0.635)和工作过程(ω
72
＝0.511)贡献因素2，规程(ω
23
＝0.602)、经验/培训(ω
43
＝0.663)、可用时间(ω
53
＝0.503)和工作过程(ω
73
＝0.787)对因素3有贡献。在该案例中，单个psf，例如规程、经验/培训和工作过程，可以贡献于多个聚类因子，这表明单个psf不仅可能影响另一个单个psf，而且可能同时对多个因素产生影响。
[0118]
比较三个案例，可以发现案例1和2都有两个中间因子，但案例2没有涉及规程psf。案例2的hep为4.1e-02，低于案例1的hep为5.6e-02，这意味着所涉及的psf数量越少，hep就越低，这显然符合实际情况，在核电厂中，较少的psfs对操纵员造成较小的负面影响。比较案例1和案例3时，可以发现两个案例涉及相同的psf数量，但案例3的中间因子比案例1多，这表明相较于案例1，psf关系的复杂性增加，案例3的hep为3.7e-02，小于案例1的hep，这意味着psf的复杂性增加导致hep减小。
[0119]
综合考虑这三种案例，复杂度、压力/压力源和职责适宜表现出稳定的相关关系，这意味着这三种psf共同作用于人员失误的概率很高，经验/培训和工作过程两个psf，可以同时贡献于不同的聚类因素，说明它们可以与许多其他psf交互，这也是它们较大概率出现在人因事件中的原因(如图3的结果所示)。
[0120]
综上，本实施例中运用89份人因事件报告验证提出的模型，结果显示，复杂度、可用时间、压力/压力源和职责适宜是高度相关的psfs，而规程、人因工程/人机界面、经验/培训和工作过程是高度相关的psfs，并且该模型能准确估计heps。需要指出的是，本实施例中
提出的模型对psf的数量并没有限制，它可以将n个psfs聚类成少量中间因子，而不会失去psf原本信息的完整性，可以弥补现有hra方法没有考虑psfs间的关系这一缺陷，相较于现有的hra方法，本实施例中所采用的方法能够减少专家判断的主观性，更准确地估算出人员失误概率。
[0121]
基于上述方法，我们还可以构建一种计算机量化预测人员失误概率的系统，具体而言，该系统中主要包括：1、数据库，存储有多种情境下影响人员失误的psfs及其条件概率分布数据。2、efa-bbn模型生成模块，用于从数据库中获取多种情境下影响人员失误的psfs并将其作为父节点，以人员失误概率作为子节点，对获取的psfs进行聚类分析，以聚类因子作为连接父节点和子节点的中间节点，构建通用bbn模型；以及，利用efa法结合当前情境条件对通用bbn模型中的psfs进行分析，生成psf对聚类因子贡献权重值的均匀分布，以对聚类因子贡献权重值大于0.5为筛选标准，对于满足该标准的psfs，保留其与中间节点的关系，对于不满足该标准的psfs，则删除其与中间节点的关系，生成当前情境条件下的efa-bbn模型。3、计算模块，用以从数据库中获取当前情境条件下的efa-bbn模型中保留的psfs的条件概率并将概率值归一化，再基于与父节点状态相关的聚类因子的概率密度函数获得中间节点的条件概率，以及利用成功似然指数法估算子节点，计算得出当前情境条件下人员失误概率的量化预测结果。当然，也可以在系统中设置一个预先存储有通用bbn模型的存储器，这样的话，efa-bbn模型生成模块就不需要先构建通用bbn模型，而可以从存储器中直接调用通用bbn模型并生成当前情境条件下的efa-bbn模型，从而减少模型构建过程中的数据运算量，提高工作效率。
[0122]
上述实施例为本发明较佳的实现方案，在不脱离本技术方案构思的前提下任何显而易见的替换均在本发明的保护范围之内。为了让本领域普通技术人员更方便地理解本发明相对于现有技术的改进之处，本发明的一些附图和描述已经被简化，并且为了清楚起见，本技术文件还省略了一些其它要素，本领域普通技术人员应该意识到这些省略的要素也可构成本发明的内容。