盲源分离方法、装置、电子设备及存储介质与流程

1.本技术涉及信号处理技术领域，具体涉及一种盲源分离方法、装置、电子设备及存储介质。


背景技术：

2.随着信息技术的发展，通信需求不断增加，电磁环境日益复杂。在实际的通信环境中，总是存在有用信号被其他信号干扰的情况，因此需要进行干扰消除，从多种混合信号中分离出有用信号，从而提升信号的解调性能。传统的用于分离出有用信号的方法计算复杂度太高，很难达到实时性，比如独立成分分析(independent component analysis)ica方法，这种方法需要进行迭代求解，计算复杂度很高，降低了计算效率。


技术实现要素：

3.本技术实施例公开了一种盲源分离方法、装置、电子设备及存储介质，能够在保持良好分离效果的前提下，降低计算复杂度。
4.本技术实施例公开一种盲源分离方法，其特征在于，所述方法包括：
5.获取两个天线分别接收到的接收信号；
6.根据待求解的第一分离矩阵和所述两个天线分别接收到的接收信号确定两个分离信号；所述待求解的第一分离矩阵是利用角度变量的三角函数运算结果构建出的二阶方阵；
7.计算所述两个分离信号的高阶累积量，以得到关于所述角度变量的第一优化函数；
8.对所述第一优化函数进行求解，以得到所述角度变量对应的角度最优解；
9.根据所述角度最优解得到求解完成的第二分离矩阵；所述第二分离矩阵用于从所述接收信号中分离出原始发射信号。
10.作为一种可选的实施方式，所述对所述第一优化函数进行求解，以得到所述角度变量对应的角度最优解，包括：
11.对所述第一优化函数求极值，以将所述第一优化函数转换成第二优化函数；
12.对所述第二优化函数进行求解，以得到所述角度变量对应的角度最优解。
13.作为一种可选的实施方式，所述对所述第二优化函数进行求解，以得到所述角度变量对应的角度最优解，包括：
14.对所述第二优化函数进行求解，以得到所述角度变量对应的两个角度解析解；
15.计算所述两个角度解析解分别对应的所述第一优化函数的函数值的平方值；
16.将所述两个角度解析解分别对应的所述第一优化函数的函数值的平方值中的最大平方值对应的角度解析解确定为所述角度变量对应的角度最优解。
17.作为一种可选的实施方式，所述两个分离信号包括：第一分离信号和第二分离信号；所述两个天线分别接收到的接收信号包括：第一接收信号和第二接收信号；所述第一分
离矩阵包括：所述角度变量的第一余弦运算结果、所述角度变量的第二余弦运算结果，以及所述角度变量的正弦运算结果；所述第二余弦运算结果是所述第一余弦运算结果的负数；所述根据待求解的第一分离矩阵和所述两个天线分别接收到的接收信号确定两个分离信号，包括：
18.根据所述第一余弦运算结果与所述第一接收信号的乘积，以及所述正弦运算结果与所述第二接收信号的乘积，确定所述第一分离信号；
19.根据所述角度变量的正弦运算结果与所述第一接收信号的乘积，以及所述第二余弦运算结果与所述第二接收信号的乘积，确定所述第二分离信号。
20.作为一种可选的实施方式，所述计算所述两个分离信号的高阶累积量，以得到关于所述角度变量的第一优化函数，包括：
21.根据所述第一分离信号的四次方的均值，以及所述第二分离信号的四次方的均值确定所述两个分离信号的四阶累积量；
22.根据所述四阶累积量得到关于所述角度变量的第一优化函数。
23.作为一种可选的实施方式，在所述根据所述角度最优解得到求解完成的第二分离矩阵之后，所述方法还包括：
24.利用所述求解完成的第二分离矩阵从所述接收信号中分离出原始发射信号。
25.作为一种可选的实施方式，在所述获取两个天线分别接收到的接收信号之后，所述方法还包括：
26.对所述两个天线分别接收到的接收信号进行零均值化，得到零均值信号数列；所述零均值信号数列包括与所述两个天线分别接收到的接收信号分别对应的零均值信号；
27.计算所述零均值信号数列的协方差矩阵，并对所述协方差矩阵进行奇异值分解，以得到白化矩阵；
28.将所述白化矩阵与所述零均值信号数列相乘，得到所述两个天线分别对应的白化处理后的接收信号；
29.所述根据待求解的第一分离矩阵和所述两个天线分别接收到的接收信号确定两个分离信号，包括：
30.根据待求解的第一分离矩阵和所述两个天线分别对应的所述白化处理后的接收信号确定两个分离信号。
31.本技术实施例公开一种盲源分离装置，所述装置包括：
32.获取模块，用于获取两个天线分别接收到的接收信号；
33.确定模块，用于根据待求解的第一分离矩阵和所述两个天线分别接收到的接收信号确定两个分离信号；所述待求解的第一分离矩阵是利用角度变量的三角函数运算结果构建出的二阶方阵；
34.计算模块，用于计算所述两个分离信号的高阶累积量，以得到关于所述角度变量的第一优化函数；
35.求解模块，用于对所述第一优化函数进行求解，以得到所述角度变量对应的角度最优解；
36.分离模块，用于根据所述角度最优解得到求解完成的第二分离矩阵；所述第二分离矩阵用于从所述接收信号中分离出原始发射信号。
37.本技术实施例公开一种电子设备，包括存储器及处理器，所述存储器中存储有计算机程序，所述计算机程序被所述处理器执行时，使得所述处理器实现本技术实施例公开的任意一种盲源分离方法。
38.本技术实施例公开一种计算机可读存储介质，其存储计算机程序，其中，所述计算机程序使得计算机执行本技术实施例公开的任意一种盲源分离方法。
39.与相关技术相比，本技术实施例具有以下有益效果：
40.根据待求解的第一分离矩阵和从两个天线分别接收到的接收信号确定两个分离信号；待求解的第一分离矩阵是利用角度变量的三角函数运算结果构建出的；根据两个分离信号的高阶累积量得到关于角度变量的第一优化函数；利用对第一优化函数进行求解得到的角度变量对应的角度最优解，得到求解完成的第二分离矩阵；第二分离矩阵用于从接收信号中分离出原始发射信号。
41.本技术实施例基于两个接收天线的场景，通过计算分离信号的高阶累积量构建第一优化函数，且对第一优化函数求解得到用于计算第二分离矩阵的角度最优解，无需通过迭代求解出用于从接收信号中分离出原始发射信号的第二分离矩阵，在保持良好分离效果的前提下极大降低了计算复杂度，提高了计算效率，能够满足通信系统中对于实时性的需求。
附图说明
42.为了更清楚地说明本技术实施例中的技术方案，下面将对实施例中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本技术的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。
43.图1是本技术实施例公开的一种盲源分离方法的流程示意图；
44.图2是本技术实施例公开的一种盲源分离效果对比图；
45.图3是本技术实施例公开的另一种盲源分离效果对比图；
46.图4是本技术实施例公开的另一种盲源分离方法的流程示意图；
47.图5是本技术实施例公开的另一种盲源分离方法的流程示意图；
48.图6是本技术实施例公开的一种盲源分离装置的结构示意图；
49.图7是本技术实施例公开的一种电子设备的结构示意图。
具体实施方式
50.下面将结合本技术实施例中的附图，对本技术实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅是本技术一部分实施例，而不是全部的实施例。基于本技术中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本技术保护的范围。
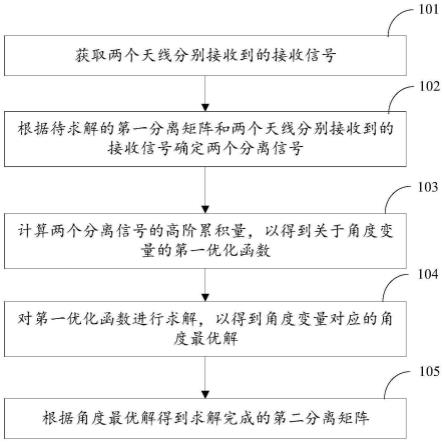
51.需要说明的是，本技术实施例及附图中的术语“包括”和“具有”以及它们任何变形，意图在于覆盖不排他的包含。例如包含了一系列步骤或单元的过程、方法、系统、产品或设备没有限定于已列出的步骤或单元，而是可选地还包括没有列出的步骤或单元，或可选地还包括对于这些过程、方法、产品或设备固有的其它步骤或单元。
52.本技术实施例公开了一种盲源分离方法、装置、电子设备及存储介质，能够在保持良好分离效果的前提下，降低计算复杂度。以下分别进行详细说明。
53.请参阅图1，图1是本技术实施例公开的一种盲源分离方法的流程示意图。其中，图1所描述的盲源分离方法适用于笔记本电脑、工业计算机等电子设备，本技术实施例不做限定。
54.盲源分离可以在不知道源信号及信号混合参数的情况下，仅根据观测到的多源混合信号估计原始源信号。其中，多源混合信号是多个信号接收源接收到的信号，可以包括有用信号、干扰信号、噪声等。
55.如图1所示，该盲源分离方法可以包括以下步骤：
56.101、获取两个天线分别接收到的接收信号。
57.本技术实施例针对两个天线的接收场景，接收信号是从天线接收到的能够直接观测的信号。
58.102、根据待求解的第一分离矩阵和两个天线分别接收到的接收信号确定两个分离信号。
59.待求解的第一分离矩阵是利用角度变量的三角函数运算结果构建出的二阶方阵。
60.三角函数运算结果可以包括正弦函数运算结果和余弦函数运算结果。
61.由于第一分离矩阵是利用角度变量构建出来的，根据第一分离矩阵和两个天线分别接收到的接收信号确定出的两个分离信号也是利用角度变量构建出来的。
62.可选的，可以将待求解的第一分离矩阵和两个天线分别接收到的接收信号相乘，以确定两个分离信号。
63.103、计算两个分离信号的高阶累积量，以得到关于角度变量的第一优化函数。
64.高阶累积量可以用于描述分离信号的统计特性；计算高阶累积量可以从分离信号中提取出非高斯信号，能够在白高斯噪声下正确估计信号源的个数。比如，高阶累积量可以是四阶累积量。第一优化函数是用于求解角度变量的最优值的优化函数。可选的，可以将两个分离信号的高阶累积量作为关于角度变量的第一优化函数。
65.104、对第一优化函数进行求解，以得到角度变量对应的角度最优解。
66.对第一优化函数进行求解，可以是通过求根公式直接求解，或者，可以进行插值求解，或者，可以对第一优化函数求极值，得到角度变量对应的角度最优解。角度最优解即角度变量对应的最优值。
67.105、根据角度最优解得到求解完成的第二分离矩阵。
68.第二分离矩阵用于从接收信号中分离出原始发射信号。
69.根据角度最优解得到求解完成的第二分离矩阵，可以是利用角度最优解替代第一分离矩阵中的角度变量，
70.接收信号中包括有用信号、干扰信号和噪声。原始发射信号可以是接收信号中的有用信号。因此第二分离矩阵可以用于从接收信号中分离出两路信号，一路信号是原始发射信号(有用信号)，一路信号是干扰信号。
71.本技术实施例基于两个接收天线的场景，通过计算分离信号的高阶累积量构建第一优化函数，且对第一优化函数求解得到用于计算第二分离矩阵的角度最优解，无需通过迭代求解出用于从接收信号中分离出原始发射信号的第二分离矩阵，在保持良好分离效果
的前提下极大降低了计算复杂度，提高了计算效率，能够满足通信系统中对于实时性的需求。
72.本技术实施例的盲源分离方法除了可以快速进行盲源分离以外，还可以达到更好的盲源分离效果。如图2所示，图2是本技术实施例公开的一种盲源分离效果对比图，用于对比本技术实施例的盲源分离方法和基于矩阵联合对角化的预白化jade方法输出的分离信号的估计精度。jade方法的计算复杂度远高于本技术实施例的盲源分离方法，图2表明本技术实施例在计算复杂度远低于jade方法的前提下，还能保持与jade方法一致的分离性能。分离信号的相似系数越接近于1，说明分离效果越好。
73.除此之外，本技术实施例的盲源分离方法分离出的信号可以保持信号的分离次序。如图3所示，图3是本技术实施例公开的另一种盲源分离效果对比图，在对分离效果进行验证时，通过有用信号s1与分离出的两路信号u
t
和v
t
进行相关，相关值大的一个为有用信号s1的分离信号。仿真1000盲源分离块，相应的分离结果如图3所示。图3左边是本技术实施例的方法，随着仿真次数的相关输出结果；图3右边是jade方法随着仿真次数的相关输出结果。本技术实施例分离出的两路信号，可以保持信号的分离次序，而jade方法分离出的两路信号，顺序是随机的。
74.因此，本技术实施例不仅能降低计算复杂度，还可以提高分离信号的估计精度，而且可以保持信号的分离次序，从而达到更好的盲源分离效果。
75.请参阅图4，图4是本技术实施例公开的另一种盲源分离方法的流程示意图，该方法可应用于前述的任意一种电子设备。如图4所示，该方法包括以下步骤：
76.401、获取两个天线分别接收到的接收信号。
77.接收信号可以是将混合矩阵作用在原始发射信号上得到的多源混合信号。混合矩阵可以用于指示多源混合信号中的信号混合参数。
78.示例性的，接收信号的接收模型可以表示为：
79.z＝as+n
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)
80.其中，a为混合矩阵，s为原始发射信号，且相互独立，n为白噪声，z为接收信号。
81.402、根据第一余弦运算结果与第一接收信号的乘积，以及正弦运算结果与第二接收信号的乘积，确定第一分离信号。
82.待求解的第一分离矩阵是利用角度变量的三角函数运算结果构建出的二阶方阵。两个分离信号包括：第一分离信号和第二分离信号；两个天线分别接收到的接收信号包括：第一接收信号和第二接收信号；第一分离矩阵包括：角度变量的第一余弦运算结果、角度变量的第二余弦运算结果，以及角度变量的正弦运算结果；第二余弦运算结果是第一余弦运算结果的负数。
83.示例性的，对待求解的第一分离矩阵w中的向量进行归一化，同时对接收信号z进行白化处理，得到白化处理后的接收信号x＝[x1；x2]。
[0084]
待求解的第一分离矩阵可以表示为：
[0085][0086]
其中，θ为中间变量；w为第一分离矩阵；cos(θ)为角度变量的第一余弦运算结果，-cos(θ)为角度变量的第二余弦运算结果，sin(θ)为角度变量的正弦运算结果。
[0087]
403、根据角度变量的正弦运算结果与第一接收信号的乘积，以及第二余弦运算结果与第二接收信号的乘积，确定第二分离信号。
[0088]
通过第一分离矩阵w对接收信号x进行分离，可以得到：
[0089]ut
＝cos(θ)x1+sin(θ)x2ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0090]vt
＝sin(θ)x
1-cos(θ)x2ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0091]
其中，u
t
为第一分离信号，v
t
为第二分离信号，cos(θ)为角度变量的第一余弦运算结果，-cos(θ)为角度变量的第二余弦运算结果，sin(θ)为角度变量的正弦运算结果，x1为第一接收信号，x2为第二接收信号。
[0092]
404、根据第一分离信号的四次方的均值，以及第二分离信号的四次方的均值确定两个分离信号的四阶累积量。
[0093]
四阶累积量的定义为：
[0094][0095]
其中，mi＝e[xi]，e[xi]表示x的i次方的均值。如果信号的均值为0，那么mi＝0。白化处理后的接收信号x的均值以及x的三次方的均值都为0，x的平方的均值为1。
[0096]
其中，两个分离信号的四阶累积量为第一分离信号的四阶累积量和第二分离信号的四阶累积量的和。
[0097]
因此两个分离信号的四阶累积量为：
[0098][0099]
其中，为第一分离信号的四次方的均值，为第二分离信号的四次方的均值。
[0100]
405、根据四阶累积量得到关于角度变量的第一优化函数。
[0101]
将公式(3)和公式(4)代入到公式(6)中，得到关于角度变量的第一优化函数为：
[0102]
f(θ)＝acos(4θ)+bsin(4θ)+c-6
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(7)
[0103]
其中，其中，第一优化函数随着角度变量θ进行变化。由于和都是常数，只需要考虑和而和都是正数，因此可以对进行求导计算极值，即求解θ的极值。
[0104]
406、对第一优化函数求极值，以将第一优化函数转换成第二优化函数。
[0105]
对第一优化函数求极值，可以是先对第一优化函数求导，再求解第一优化函数的导数等于0时的根，此时可以得到第二优化函数。
[0106]
第二优化函数可以表示为：
[0107][0108]
407、对第二优化函数进行求解，以得到角度变量对应的两个角度解析解。
[0109]
对第二优化函数进行求解，可以得到由于函数具有模糊性，因此
[0110]
因此两个角度解析解分别为：
[0111]
以及
[0112]
408、计算两个角度解析解分别对应的第一优化函数的函数值的平方值。
[0113]
409、将两个角度解析解分别对应的第一优化函数的函数值的平方值中的最大平方值对应的角度解析解确定为角度变量对应的角度最优解。
[0114]
比较f(θ1)2和f(θ2)2，如果f(θ1)2》f(θ2)2，则否则
[0115]
其中，f(θ1)2为角度变量为θ1时对应的第一优化函数的函数值的平方值；f(θ2)2为角度变量为θ2时对应的第一优化函数的函数值的平方值；为角度变量对应的角度最优解。
[0116]
410、根据角度最优解得到求解完成的第二分离矩阵。
[0117]
将角度最优解代入到公式(2)的待求解的第一分离矩阵中，得到第二分离矩阵表示为：
[0118][0119]
411、利用求解完成的第二分离矩阵从接收信号中分离出原始发射信号。
[0120]
利用第二分离矩阵可以从接收信号中分离出两路信号，一路为原始发射信号(有用信号)，一路为干扰信号。即，利用第二分离矩阵w可以从接收信号x中分离出原始发射信号s。
[0121]
接收信号中包括有用信号、干扰信号和噪声。原始发射信号可以是接收信号中的有用信号。因此分离矩阵可以用于从接收信号中分离出有用信号。
[0122]
本技术实施例通过利用角度变量的三角函数运算结果构造出接收信号的数学模型，再通过高阶累积量构建第一优化函数，给出解析的计算方法，不需要迭代，进而极大的降低了计算复杂度，同时还保持了基于高阶累积量方法的较好的分离性能。在数字突发传输系统中，本技术实施例通过对第一优化函数求导计算极值，直接通过求解第二优化函数得到第二分离矩阵，在保持分离性能的前提下降低了计算复杂度，极大提升了计算效率，而且保持了相邻分离块输出信号的相位一致性。
[0123]
请参阅图5，图5是本技术实施例公开的另一种盲源分离方法的流程示意图，该方法可应用于前述的任意一种电子设备。如图5所示，该方法包括以下步骤：
[0124]
501、获取两个天线分别接收到的接收信号。
[0125]
两个天线分别接收到的接收信号包括白化处理前的第一接收信号和第二接收信号。
[0126]
白化处理前的接收信号可以表示为z＝[z1；z2]，其中z1和z2为第一接收信号和第二接收信号。
[0127]
502、对两个天线分别接收到的接收信号进行零均值化，得到零均值信号数列。
[0128]
零均值信号数列包括与两个天线分别接收到的接收信号分别对应的零均值信号。
[0129]
计算接收信号的均值z{x}，将第一接收信号和第二接收信号分别减去均值e{z}，得到第一接收信号和第二接收信号分别对应的零均值信号，以对接收信号进行零均值化，计算得到的零均值信号数列为
[0130]
503、计算零均值信号数列的协方差矩阵，并对协方差矩阵进行奇异值分解，以得到白化矩阵。
[0131]
计算零均值信号数列的协方差矩阵由于协方差矩阵是方阵，对其进行特征值分解，即可得到特征向量和特征值矩阵[e，d]＝svd(r)，其中，e为特征向量空间，d为特征值空间。通过e和d可以构建白化矩阵v＝(d-σi)-1/2
e。
[0132]
504、将白化矩阵与零均值信号数列相乘，得到两个天线分别对应的白化处理后的接收信号。
[0133]
将白化矩阵v作用于零均值信号数列可以得到零均值、单位方差的白化处理后的接收信号根据特征向量的性质，白化处理后的接收信号x中各个分量互不相关。
[0134]
步骤502～504去除了接收信号中第一接收信号和第二接收信号的信号相关性，简化了后续对原始发射信号的提取过程。
[0135]
本技术实施例通过对接收信号进行零均值化、求协方差矩阵以及奇异值分解，得到白化矩阵；利用白化矩阵对接收信号进行预处理，降低接收信号中各个信号的相关性，以得到白化处理后的接收信号，有利于提高后续从白化处理后的接收信号中提取出原始发射信号的效率。
[0136]
505、根据待求解的第一分离矩阵和两个天线分别对应的白化处理后的接收信号确定两个分离信号。
[0137]
其中，两个分离信号可以是通过第一分离矩阵和白化处理后的接收信号相乘得到的。
[0138]
506、计算两个分离信号的高阶累积量，以得到关于角度变量的第一优化函数。
[0139]
507、对第一优化函数进行求解，以得到角度变量对应的角度最优解。
[0140]
508、根据角度最优解得到求解完成的第二分离矩阵。
[0141]
第二分离矩阵用于从接收信号中分离出原始发射信号。
[0142]
本技术实施例针对于两个天线的接收场景，基于高阶累积量建立第一优化函数，对第一优化函数进行解析求解得到第二分离矩阵，可以从接收信号中分离出干净的有用信号，在保证干扰消除效果的情况下极大地降低了计算复杂度，提升了计算效率，满足了通信系统中对于实时性的要求，提升了信号的解调性能。
[0143]
请参阅图6，图6是本技术实施例公开的一种盲源分离装置的结构示意图。该装置可应用于笔记本电脑、工业计算机等电子设备，具体不做限定。如图6所示，盲源分离装置600可包括：获取模块610、确定模块620、计算模块630、求解模块640、分离模块650。
[0144]
获取模块610，用于获取两个天线分别接收到的接收信号；
[0145]
确定模块620，用于根据待求解的第一分离矩阵和两个天线分别接收到的接收信号确定两个分离信号；待求解的第一分离矩阵是利用角度变量的三角函数运算结果构建出的二阶方阵；
[0146]
计算模块630，用于计算两个分离信号的高阶累积量，以得到关于角度变量的第一优化函数；
[0147]
求解模块640，用于对第一优化函数进行求解，以得到角度变量对应的角度最优解；
[0148]
分离模块650，用于根据角度最优解得到求解完成的第二分离矩阵；第二分离矩阵用于从接收信号中分离出原始发射信号。
[0149]
在一个实施例中，求解模块640，还用于对第一优化函数求极值，以将第一优化函数转换成第二优化函数；对第二优化函数进行求解，以得到角度变量对应的角度最优解。
[0150]
在一个实施例中，求解模块640，还用于对第二优化函数进行求解，以得到角度变量对应的两个角度解析解；计算两个角度解析解分别对应的第一优化函数的函数值的平方值；将两个角度解析解分别对应的第一优化函数的函数值的平方值中的最大平方值对应的角度解析解确定为角度变量对应的角度最优解。
[0151]
在一个实施例中，两个分离信号包括：第一分离信号和第二分离信号；两个天线分别接收到的接收信号包括：第一接收信号和第二接收信号；第一分离矩阵包括：角度变量的第一余弦运算结果、角度变量的第二余弦运算结果，以及角度变量的正弦运算结果；第二余弦运算结果是第一余弦运算结果的负数；确定模块620，还用于根据第一余弦运算结果与第一接收信号的乘积，以及正弦运算结果与第二接收信号的乘积，确定第一分离信号；根据角度变量的正弦运算结果与第一接收信号的乘积，以及第二余弦运算结果与第二接收信号的乘积，确定第二分离信号。
[0152]
在一个实施例中，计算模块630，还用于根据第一分离信号的四次方的均值，以及第二分离信号的四次方的均值确定两个分离信号的四阶累积量；
[0153]
根据四阶累积量得到关于角度变量的第一优化函数。
[0154]
在一个实施例中，盲源分离装置600还可用于利用求解完成的第二分离矩阵从接收信号中分离出原始发射信号。
[0155]
在一个实施例中，盲源分离装置600还可用于对两个天线分别接收到的接收信号进行零均值化，得到零均值信号数列；零均值信号数列包括与两个天线分别接收到的接收信号分别对应的零均值信号；计算零均值信号数列的协方差矩阵，并对协方差矩阵进行奇异值分解，以得到白化矩阵；将白化矩阵与零均值信号数列相乘，得到两个天线分别对应的白化处理后的接收信号；确定模块620，还用于根据待求解的第一分离矩阵和两个天线分别对应的白化处理后的接收信号确定两个分离信号。
[0156]
请参阅图7，图7是本技术实施例公开的一种电子设备的结构示意图。
[0157]
如图7所示，该电子设备700可以包括：
[0158]
存储有可执行程序代码的存储器710；
[0159]
与存储器710耦合的处理器720；
[0160]
其中，处理器720调用存储器710中存储的可执行程序代码，执行本技术实施例公开的任一种盲源分离方法。
[0161]
本技术实施例公开一种计算机可读存储介质，其存储计算机程序，其中，计算机程序被所述处理器执行时，使得所述处理器实现本技术实施例公开的任意一种盲源分离方法。
[0162]
应理解，说明书通篇中提到的“一个实施例”或“一实施例”意味着与实施例有关的特定特征、结构或特性包括在本技术的至少一个实施例中。因此，在整个说明书各处出现的“在一个实施例中”或“在一实施例中”未必一定指相同的实施例。此外，这些特定特征、结构或特性可以以任意适合的方式结合在一个或多个实施例中。本领域技术人员也应该知悉，说明书中所描述的实施例均属于可选实施例，所涉及的动作和模块并不一定是本技术所必须的。
[0163]
在本技术的各种实施例中，应理解，上述各过程的序号的大小并不意味着执行顺序的必然先后，各过程的执行顺序应以其功能和内在逻辑确定，而不应对本技术实施例的实施过程构成任何限定。
[0164]
上述作为分离部件说明的单元可以是或者也可以不是物理上分开的，作为单元显示的部件可以是或者也可以不是物单元，即可位于一个地方，或者也可以分布到多个网络单元上。可根据实际的需要选择其中的部分或全部单元来实现本实施例方案的目的。
[0165]
另外，在本技术各实施例中的各功能单元可以集成在一个处理单元中，也可以是各个单元单独物理存在，也可以两个或两个以上单元集成在一个单元中。上述集成的单元既可以采用硬件的形式实现，也可以采用软件功能单元的形式实现。
[0166]
上述集成的单元若以软件功能单元的形式实现并作为独立的产品销售或使用时，可以存储在一个计算机可获取的存储器中。基于这样的理解，本技术的技术方案本质上或者说对现有技术做出贡献的部分或者该技术方案的全部或者部分，可以以软件产品的形式体现出来，该计算机软件产品存储在一个存储器中，包括若干请求用以使得一台计算机设备(可以为个人计算机、服务器或者网络设备等，具体可以是计算机设备中的处理器)执行本技术的各个实施例上述方法的部分或全部步骤。
[0167]
本领域普通技术人员可以理解上述实施例的各种方法中的全部或部分步骤是可以通过程序来指令相关的硬件来完成，该程序可以存储于一计算机可读存储介质中，存储介质包括只读存储器(read-only memory，rom)、随机存储器(random access memory，ram)、可编程只读存储器(programmable read-only memory，prom)、可擦除可编程只读存储器(erasable programmable read only memory，eprom)、一次可编程只读存储器(one-time programmable read-only memory，otprom)、电子抹除式可复写只读存储器(electrically-erasable programmable read-only memory，eeprom)、只读光盘(compact disc read-only memory，cd-rom)或其他光盘存储器、磁盘存储器、磁带存储器、或者能够用于携带或存储数据的计算机可读的任何其他介质。
[0168]
以上对本技术实施例公开的一种盲源分离方法、装置、电子设备及存储介质进行了详细介绍，本文中应用了具体个例对本技术的原理及实施方式进行了阐述，以上实施例的说明只是用于帮助理解本技术的方法及其核心思想。同时，对于本领域的一般技术人员，依据本技术的思想，在具体实施方式及应用范围上均会有改变之处，综上所述，本说明书内容不应理解为对本技术的限制。