一种考虑工程噪声影响的老采空区地表沉降预测方法

：
1.本发明涉及地下工程技术领域，尤其涉及一种考虑工程噪声影响的老采空区地表沉降预测方法。


背景技术：

2.采空区是由人为挖掘或者天然地质运动在地表下面产生的“空洞”，采空区的存在使得矿山的安全生产面临很大的安全问题，随着经济社会的飞速发展，对矿产品的需求越来越大，很多矿物需要地下开采，矿物的大量开采会留下大面积的采空区，由于地下采空区具有隐伏性强、空间分布特征规律性差、采空区顶板冒落塌陷情况难以预测等特点，因此，为了保证建筑构物的正常使用寿命和人民生命财产安全，采空区地表沉降预测分析的必要性和重要性愈加明显。
3.采空区沉降预测方法主要有传统理论分析方法、物理数值模拟方法及基于人工智能和大数据的智能预测方法等。
4.传统理论分析方法主要有影响函数法、经验手段法、剖面函数法等，这类分析方法均假设采空区是规则形状，故仅适用于规则采空区，同时传统理论分析方法需要大量的实测资料，当实测资料不足时，无法得到准确的预测参数。
5.物理数值模拟方法主要有模型实验法、有限元法、有限差分法和离散元法等，这类分析方法需要能够准确还原采空区三维结构，且对岩体参数的取值要求高，在缺乏实测资料的情况下，物理数值模拟的结果往往偏差较大，不能为工程所接受。
6.智能预测方法主要有时间序列模型法、灰色预测法和神经网络法等，这类分析方法目前已得到广泛应用，但仍存在一定缺陷，如时间序列法和灰色预测法不能对沉降进行滚动预测，广泛应用的bp神经网络和rnn循环神经网络，在预测时容易出现梯度消失和梯度爆炸问题，从而造成预测结果不收敛。lstm循环神经网络解决了这一问题，能够对采空区地表沉降做出高精度的预测，但是在这些采空区地表沉降预测方法中，均未考虑工程噪声对沉降预测的影响。在对实际工程监测点进行沉降监测时，由于受到天气、水文和施工等各种随机因素的干扰，采集的沉降数据包含了各种噪声，这些噪声的存在，会使得预测精度受到影响。
7.自回归模型是一种对平稳时间序列进行预测的模型，仅适用于数据的历史分布与未来分布趋于一致的情况，如城市的交通量、城市的用电量、人口的增长量、矿的开采量、河水的流量、股市的价格、景点的游客数量和国民的收入等，即适合预测受历史因素影响较大的数据。而沉降数据随着时间的推移一般呈增长趋势，未来沉降量分布受历史沉降量分布的影响较小，故自回归模型一般难以直接用于沉降预测。
8.daubechies(db)小波分解降噪目前已成功应用于多个领域，但并未应用在老采空区地表沉降预测领域中，针对上述情况，设计人员需要一种考虑工程噪声的老采空区地表沉降预测方法，来满足目前状况的需求。


技术实现要素：

9.为了弥补现有技术问题的不足，本发明的目的是提供一种考虑工程噪声影响的老采空区地表沉降预测方法，通过db小波对原始沉降监测数据进行去噪分解，充分考虑了工程监测数据噪声对沉降预测精度的影响；分解后的低频趋势项采用适合预测趋势性数据的lstm进行预测，高频噪声项采用适合预测平稳时间序列(高频噪声项呈现平稳序列)的ar模型进行预测，充分发挥了各个模型的预测优势，有利于提高预测精度；可有效减少测量数据噪声引起的预测误差，相较于单一模型和传统模型，预测精度更高、误差更小、趋势更好，提高了老采空区地表沉降预测精度。
10.本发明的技术方案如下：
11.一种考虑工程噪声影响的老采空区地表沉降预测方法，其特征在于，包括如下步骤：
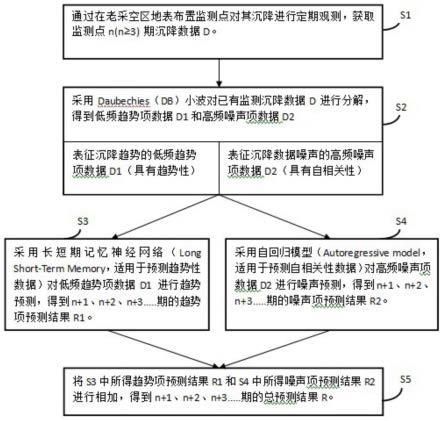
12.s1、通过在老采空区地表布置监测点对其沉降进行定期观测，获取每个监测点n期沉降数据d，其中n≥3；
13.s2、采用db小波对已有监测沉降数据进行分解，得到表征沉降趋势的低频趋势项数据d1和表征沉降数据噪声的高频噪声项数据d2；
14.s3、采用长短期记忆神经网络模型对低频趋势项数据d1进行趋势预测，得到n+1、n+2、n+3
……
期的趋势项预测结果r1；
15.s4、采用自回归模型对高频噪声项数据d2进行噪声预测，得到n+1、n+2、n+3
……
期的噪声项预测结果r2；
16.s5、将s3中所得趋势项预测结果r1和对应s4中所得噪声项预测结果r2进行相加，得到n+1、n+2、n+3
……
期的总预测结果r。
17.所述的考虑工程噪声影响的老采空区地表沉降预测方法，其特征在于，所述的s2具体包括步骤：
18.1)、选取不同db小波分解每个监测点n期沉降数据d，得到不同db小波下的低频趋势项数据d
′
1和高频噪声项数据d
′
2；
19.2)、计算不同低频趋势项数据d
′
1的均方根误差；
20.3)、计算不同高频噪声项数据d
′
2的信噪比；
21.4)、确定计算小波：寻找均方根误差的最小值和信噪比的最大值所对应的db小波为计算小波，若均方根误差的最小值和信噪比的最大值分别位于不同db小波，以均方根误差的最小值所对应的db小波为计算小波；
22.5)、利用计算小波所分解的低频趋势项数据d
′
1和高频噪声项数据d
′
2分别作为d1和d2。
23.本发明的优点是：
24.1、本发明通过db小波对原始沉降监测数据进行去噪分解，充分考虑了工程监测数据噪声对沉降预测精度的影响；
25.2、本发明分解后的低频趋势项采用适合预测趋势性数据的lstm进行预测，高频噪声项采用适合预测平稳时间序列(高频噪声项呈现平稳序列)的ar模型进行预测，充分发挥了各个模型的预测优势，有利于提高预测精度；
26.3、本发明可有效减少测量数据噪声引起的预测误差，相较于单一模型和传统模
型，预测精度更高、误差更小、趋势更好，可作为提高老采空区地表沉降预测精度的一种计算方法；
27.4、本发明结合计算机，通过python或matlab语言进行编程后，能够快速的对地表沉降监测点进行预测，提高了沉降预测效率。
附图说明：
28.图1为本发明的方法流程示意图。
29.图2为本发明步骤s2的细分步骤流程示意图。
30.图3为本发明kq1监测点lstm-ar沉降预测数据对比示意图。
31.图4为本发明kq2监测点lstm-ar沉降预测数据对比示意图。
32.图5为本发明kq3监测点lstm-ar沉降预测数据对比示意图。
33.图6为本发明kq4监测点lstm-ar沉降预测数据对比示意图。
34.图7为本发明kq5监测点lstm-ar沉降预测数据对比示意图。
35.图8为kq1监测点lstm单一模型沉降预测数据对比示意图。
36.图9为kq2监测点lstm单一模型沉降预测数据对比示意图。
37.图10为kq3监测点lstm单一模型沉降预测数据对比示意图。
38.图11为kq4监测点lstm单一模型沉降预测数据对比示意图。
39.图12为kq5监测点lstm单一模型沉降预测数据对比示意图。
40.图13为kq1监测点gm(1,1)模型沉降预测数据对比示意图。
41.图14为kq2监测点gm(1,1)模型沉降预测数据对比示意图。
42.图15为kq3监测点gm(1,1)模型沉降预测数据对比示意图。
43.图16为kq4监测点gm(1,1)模型沉降预测数据对比示意图。
44.图17为kq5监测点gm(1,1)模型沉降预测数据对比示意图。
具体实施方式：
45.下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。
46.一种考虑工程噪声影响的老采空区地表沉降预测方法，其特征在于，包括如下步骤：
47.s1、通过在老采空区地表布置监测点对其沉降进行定期观测，获取每个监测点n期沉降数据d，其中n≥3；
48.s2、采用db小波对已有监测沉降数据进行分解，得到表征沉降趋势的低频趋势项数据d1和表征沉降数据噪声的高频噪声项数据d2；
49.s3、采用长短期记忆神经网络模型对低频趋势项数据d1进行趋势预测，得到n+1、n+2、n+3
……
期的趋势项预测结果r1；
50.s4、采用自回归模型对高频噪声项数据d2进行噪声预测，得到n+1、n+2、n+3
……
期的噪声项预测结果r2；
51.s5、将s3中所得趋势项预测结果r1和对应s4中所得噪声项预测结果r2进行相加，得到n+1、n+2、n+3
……
期的总预测结果r。
52.考虑工程噪声影响的老采空区地表沉降预测方法，s2具体包括步骤：
53.1)、选取不同db小波分解每个监测点n期沉降数据d，得到不同db小波下的低频趋势项数据d
′
1和高频噪声项数据d
′
2；
54.2)、计算不同低频趋势项数据d
′
1的均方根误差；
55.3)、计算不同高频噪声项数据d
′
2的信噪比；
56.4)、确定计算小波：寻找均方根误差的最小值和信噪比的最大值所对应的db小波为计算小波，若均方根误差的最小值和信噪比的最大值分别位于不同db小波，以均方根误差的最小值所对应的db小波为计算小波；
57.5)、利用计算小波所分解的低频趋势项数据d
′
1和高频噪声项数据d
′
2分别作为d1和d2。
58.本发明实际过程中，在老采空区地表多个区域进行监测点布置，并进行了定期观测；每个区域布置五个监测点对其沉降进行定期观测，监测点标记为：kq1、kq2、kq3、kq4、kq5，监测期数为35期。
59.其中某一区域的五个监测点，监测数据如表1：
60.表1沉降监测数据\mm
[0061][0062]
上述区域的五个监测点，采用本发明方法与lstm单一模式、传统模式得到的预测值与实测值平均误差绝对值\mm如表2：
[0063]
表2预测值与实测值平均误差绝对值\mm
[0064][0065]
从上述表1和表2中的监测数据采用本发明方法看出如下数据：
[0066]
地表布置监测点,通过本发明步骤s
1-s5得出监测点kq1-kq5沉降测数据与实际值的平均误差值：0.206mm、0.112mm、0.151mm、0.102mm、0.111mm；
[0067]
采用lstm单一模式得出监测点kq1-kq5沉降测数据与实际值的平均误差值：0.455mm、0.197mm、0.226mm、0.184mm、0.189mm；
[0068]
采用传统模式得出监测点kq1-kq5沉降测数据与实际值的平均误差值：1.013mm、0.734mm、0.423mm、0.709mm、0.740mm。
[0069]
从上述表1和表2中的监测数据采用本发明方法得出如下结论：
[0070]
综上，本发明可有效减少测量数据噪声引起的预测误差，相较于单一模型和传统模型，预测精度更高、误差更小、趋势更好，可作为提高采空区地表沉降预测精度的方法。
[0071]
进一步的，可以通过本发明方法进行预测：采用n＝5的预测方式预测n+1、......、n+5项，即通过第1-5项低频趋势项预测第6-10项，在更新6-10项低频趋势项后，以1-10项预测第11-15项，以此类推，直至预测第31-35项。
[0072]
最后，考虑工程噪声影响的老采空区地表沉降预测方法，结合计算机，通过python或matlab语言进行编程后，该种计算程序(可以利用现有的db小波计算程序、长短期记忆神经网络程序、自回归模型程序进行简单编程可得，这里不在赘述)快速对地表沉降监测点进行预测。
[0073]
上述需要说明的是，虽然小波分解降噪目前已成功应用于多个领域，但并未应用在老采空区地表沉降预测领域中。因此本发明通过采用daubechies(db)小波对采空区实测沉降数据进行分解，将其分解成低频趋势项和高频噪声项，长短期记忆神经网络模型(long short-term memory，适用于预测趋势性数据)，即ltsm模型适合预测趋势性的数据，所以低频趋势项采用长短期记忆神经网络模型ltsm进行预测；而自回归模型(autoregressive model，适用于预测自相关性数据)，即ar模型适合预测平稳时间序列，所以高频噪声项采用ar模型进行预测。
[0074]
综上，通过db小波将原始沉降数据中的噪声分解出来，充分的考虑了噪声对沉降预测的影响。
[0075]
尽管已经示出和描述了本发明的实施例，对于本领域的普通技术人员而言，可以理解在不脱离本发明的原理和精神的情况下可以对这些实施例进行多种变化、修改、替换和变型，本发明的范围由所附权利要求及其等同物限定。