一种多有源桥型电力电子变压器简化电磁暂态等效模型

1.本发明涉及一种多有源桥型电力电子变压器简化电磁暂态等效模型，属于电力系统电磁暂态仿真技术领域。


背景技术：

2.电力电子变压器(power electronic transformers，pet)是柔性直流配电网的关键设备，能够实现电压变换和功率传递等功能，其仿真与等效建模技术已取得较好进展。但由于其高频特征导致仿真步长小，功率模块包含高频链环节，结构复杂、连接方式多样，对其进行电磁暂态仿真将面临更为复杂的问题。特别是在多有源桥等场合下仿真效率依然较低，需要进行再次提速。
3.本发明针对具有更高复杂度、更多节点数的mab型pet拓扑存在精度或速度上的局限性的问题，提出了一种多有源桥型电力电子变压器简化电磁暂态等效模型。该方法从chb-mab型变换器入手，以isop型chb-mab变换器为算例，将广义状态空间平均法与开关函数模型相结合，以串联侧叠加等效电压源、并联侧输出总电流为切入点，最终建立了isop型chb-mab变换器简化电磁暂态等效模型，在保证一定精度的同时实现仿真加速。


技术实现要素：

4.本发明提供一种多有源桥型电力电子变压器简化电磁暂态等效模型，该方法的建立包括以下步骤：
5.步骤1：以mab型pet为例，首先建立其时域状态方程，对开关函数及状态变量傅里叶变换后可得傅里叶分解的时变非线性微分方程。
6.步骤2：采用开关函数法，将chb划分为四种电路工作状态，进而得到其两侧交直流电压、电流之间的关系。
7.步骤3：mab单元等效模型的基础上，分析多种模块间连接方式，串联侧由总的输入电流得到每个chb-mab单元的输入电流，并联侧改变系统方程进而使总电流作为方程所需量。
8.步骤4：将pet等效模型与外电路结合，进行emt解算，形成可与外部拓扑直接相连的chb-mab变换器四端口电压源等效电路。
附图说明
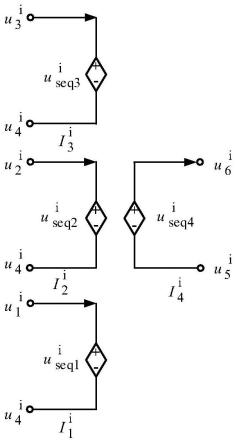
9.图1为isop型chb-mab变换器拓扑图
10.图2为mab单元拓扑图
11.图3为h桥的导通特性图
12.图4为isop型级联方式计算流程示意图
13.图5为isop型chb-mab变换器等效建模流程示意图
14.图6为isop型chb-mab变换器的等效电路(摘要附图)
具体实施方式
15.本发明提供一种多有源桥型电力电子变压器简化电磁暂态等效模型。下面将对本发明的建模步骤做进一步详细的说明。
16.步骤1：
17.图1所示崇礼pet拓扑给出了单个功率模块结构(包含chb、mab)及功率模块间的连接方式。mab由多个与高频变压器相连的有源桥组成，其常与级联h桥(chb)联合使用以实现三相ac/dc变换。
18.针对如图2所示mab单元建立时变非线性微分方程。选取高频变压器等效电感l1的电流i
l1
、电容电压u
c1
,u
c4
为状态变量；将igbt及反并联二极管用开关函数模型处理，分别对高频变压器等效电感、电容列写微分方程；对状态变量进行傅里叶分解并引入新的状态变量矩阵，最终将非线性微分方程傅里叶分解。
19.首先对高频变压器等效电感l1、电容c1、c4列写状态方程：
[0020][0021]
式(1)中各电气量均由图2给出，uh(t)和u
l
(t)分别为高频变压器一次侧和二次侧的交流电压；i
lh
(t)和i
ll
(t)别为高频变压器一次侧和二次侧的电流；l1为三相高频变压器中a相单个绕组的等效电感；n为高频变压器a相变比。
[0022]
将igbt和反并联二极管用开关函数模型处理，方波电压uh(t),u
l
(t)和电流i
lh
(t),i
ll
(t)可以用开关函数s1(t),s2(t)及状态变量u
c1
(t),u
c4
(t),i
l1
(t)表示：
[0023][0024]
式中：
[0025][0026]
式(3)中：为uh(t)外移相角；为u
l
(t)外移相角；周期t为mab全桥换流单元动作频率倒数。
[0027]
结合式(1)、(2)，可得mab的a相微分方程：
[0028][0029]
式(4)中p＝[i
l1
(t)u
c1
(t)u
c4
(t)]
t
表示系统状态变量；i
l1
(t)为包含基波和所有谐波的变压器等效电感电流量；s为系统状态变量矩阵，是主要由开关函数s1(t),s2(t)构成的3
×
3阶矩阵，由式(5)给出；i表示系统输入变量。
[0030][0031]
由于全桥换流单元开关动作频率较快，对开关函数进行傅里叶变换，可得式(6)
[0032][0033]
根据傅里叶系数卷积特性，可得：
[0034][0035]
根据工程需求可以选择直流量、基波及更高次谐波分量进行等效，本文模型等效只考虑等效电感电流的基波及3、5次谐波和电容电压的直流分量。进而，得到由各状态变量的傅里叶系数描述的mab单元简化电磁暂态等效模型微分方程：
[0036][0037]
式(8)中p，与式(4)相似，表示系统状态变量及其微分，但矩阵中仅包含电容电压直流量和等效电感电流的基波及3、5次谐波；相比式(4)，矩阵p中高频变压器等效电感电流进一步傅里叶变换；矩阵i仍系统输入变量，并提取式(5)中电流直流量，如式(9)。
[0038][0039]
以下给出矩阵详细内容如式(10)-(12)，式中w
x
值为1、3或5，可分别代表1、3、5次分量。式(10)中矩阵t
lx
反应各次电感电流之间的耦合关系；矩阵反应各次等效电感电流微分与电容电压直流量的关系；矩阵t
cx
反应电容电压微分分别与电感电流基波及3、5次谐波的关系。
[0040]wx
＝[0 jxω] (4)
[0041][0042][0043]
将状态变量的傅里叶系数表示为复数，即
[0044][0045]
傅里叶分解后的状态变量(13)代入变换后的微分方程(8)，可以得到状态变量实部和虚部分别表示的时变非线性微分方程。为增加公式通用性，给出高频变压器等效电感电流按照基波及1、3
…
k(k为奇数)次谐波分解的时变非线性微分方程如式(14)。
[0046][0047]
由(13)可知，状态变量的傅里叶系数由实部和虚部q表示，将式(8)矩阵p，转换为
q,如式(15)。
[0048][0049]
为化简矩阵内容，提出系统状态变量矩阵常系数1/π，因此wk转换为式(16)；如式(17)、(18)所示，矩阵t
lk
,t
ck
经系数提取与公式化简后略有变化。
[0050][0051][0052][0053]
方程(14)给出高频变压器等效电感电流按基波及3、5
……
k(k为奇数)次谐波分解的时变非线性微分方程，其仅对mab拓扑a相等效建模，b、c相同理。由式(14)可知基波及各次谐波方程间不存在耦合关系，因此扩展k次谐波方程时直接增加wk,t
lk
,t
ck
矩阵即可。
[0054]
步骤2：
[0055]
chb的核心拓扑为h桥，与mab全桥换流单元不同，chb工作频率一般为几百赫兹，等效过程中将其按照电路工作状态划分仍能保证模型速度，因此采用开关函数法，图3给出chb的四种工作状态。
[0056]
根据chb中各个igbt的导通信号，可得到其两侧交直流电压、电流之间的关系，如表1所示，其中s1、s2、s3、s4表示igbt导通状态，un为交流侧电压，ih为交流侧电流。
[0057]
表1igbt开关状态
[0058][0059]
表1通过导通信号将chb划分出四种工作状态，其两侧交直流电压、电流分别对应三种不同的关系。这种方法无需高频链解耦、预处理等过程，可以迅速建立交流侧与直流侧的联系，在保证模型精度的同时提高计算速度。
[0060]
步骤3：
[0061]
pet在电压和容量方面存在限制，而采用模块串并联结构组合而成的pet拓扑可满足不同的电压和功率需求。模块组合型pet大致分为4种基本类型：输入并联输出串联型(input parallel output series，ipos)、输入串联输出并联型(input series output parallel，isop)、输入串联输出串联型(input series output series,isos)和输入并联输出并联型(input parallel output parallel，ipop)。图1为多个chb-mab单元构成的isop型变换器，高压交流侧通过各单元间的串联分压，降低了对左侧h桥器件的耐压要求；低压侧通过各单元间的并联均分电流，降低了对右侧h桥器件的耐流要求。
[0062]
由于isop型级联方式包含串联、并联两种级联方式，在仿真过程中可以推及其他级联类型，因此本文以isop型结构为例，给出简化电磁暂态等效模型的建立过程，计算流程图如图4所示。判断各单元的连接方式后，分别根据串并联结构的电流特性，输入侧由总的输入电流得到每个chb-mab单元的输入电流，输出侧改变系统方程进而使总电流作为方程所需量。
[0063]
步骤4：
[0064]
如图5所示，求解过程可以分为读取系统参数及chb导通信号、正解mab单元端口电压值、反解得到端口电流值、进一步形成循环迭代，最终完成求解工作。
[0065]
由于pet的模块化结构，其状态可由控制信号决定，图6所示流程图通过更新chb导通信号实现各个h桥工作状态的即时改变。把mab参数与端口电流值相结合，可以求得图6中四个端口的电压值。在pscad/emtdc仿真中可将电压值与外电路相结合，求得端口电流值。
[0066]
最后应当说明的是：所描述的实施例仅是本技术一部分实施例，而不是全部的实施例。基于本技术中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本技术保护的范围。