一种基于移动平面与矩阵计算有理参数曲面的交的方法

1.本发明涉及cad/cam和几何建模领域，更具体的说是涉及一种基于移动平面与矩阵计算有理参数曲面的交的方法。


背景技术：

2.求两个有理参数曲面是cad/cam和几何建模中最基本的问题之一，它对边界生成，网格生成，绘制，隐藏面去除和制造都至关重要，一种快速，鲁棒，精确和拓扑正确的曲面交算法在这些应用中需求是很高的，特别是人们普遍认为cad系统可靠性差的最大原因是缺乏拓扑一致的曲面交算法。
3.一般来说两个有理曲面的交点是十分复杂的。例如，两个双三次曲面的相交曲线可以是324次代数曲线，他可能包含数百个小环和大量的奇点，一个好的交算法应该在短时间内正确的计算出所有这些特征。
4.对曲面交的探讨已有非常丰富的文献。典型的方法有代数方法(r.f.sarraga,algebraic methods for intersection,computer vision graphics and image processing 22(2)(1983)222
–
238.)，追踪法(c.bajaj,c.hoffmann,r.lynch,j.hopcroft,tracing surface intersections,computer aided geometric design 5(4)(1988)285
–
307)，格点法(hoffmann,geometric and solid modeling:an introduction,morgan kaufmann,san mateo,ca,1989)，细分法(n.patrikalakis,surface-to-surface intersections,computer graphics and applications,ieee 13(1993)89
–
95)，同伦方法，以及混合方法(s.krishnan,d.manocha,an efficient surface intersection algorithm based on lower-dimensional formulation,acm trans.graph.16(1)(1997)74
–
106.)不同的方法有各自的优缺点。例如，代数方法中，通常需要隐式化一个表面，在很大程度上保留了交上的小环路和奇点等几何特征。然而，如何隐式化就是一个很具有挑战的问题(x.jia,x.shi,f.chen,survey on the theory and applications ofμ-bases for rational curves and surfaces,journal of computational and applied mathematics 329(2018)2-23)，追踪法是许多cad系统中广泛采用的一种方法，它通常先在相交曲线上计算特征点，然后从这些点出发，沿着计算的方向对曲线进行追踪。完整的起始点计算需要精确，高效地求解一个多项式方程系统，在跟踪过程中不易避免交点曲线不同分支之间的跳跃或回路。格点法和细分法是计算相交曲线上的离散点的常用办法，但通常效率不高，容易忽略小环路和孤立点。因此，如何解决上述问题是本领域技术人员亟需研究的。


技术实现要素：

5.有鉴于此，本发明提供了一种基于移动平面与矩阵计算两个有理参数曲面的交的方法，以解决背景技术中的问题。
6.为了实现上述目的，本发明采用如下技术方案：
7.一种基于移动平面与矩阵计算有理参数曲面的交的方法，包括以下步骤：
8.输入待拟合有理参数曲面；
9.计算出第一有理参数曲面的矩阵表示；
10.将第二有理参数曲面的参数代入第一有理参数曲面至矩阵表示中，利用步进法求出参数坐标点；
11.将参数坐标点分类为不同的参数分支并转化为三维空间中的分支；
12.根据第一有理参数曲面计算出的边界点将三维空间中的分支分为几段，去掉多余的段，得到参数化结果；
13.利用新的参数化结果再次进行参数曲面拟合最终得到产品模型。
14.可选的，用步进法求出第二有理参数曲面中的参数集，参数集满足与带入后使第一有理参数曲面的矩阵表示的行列为0的参数对的距离小于ε，则将参数对连接起来。
15.可选的，如果两个参数对属于相邻的网格，则这两个参数对属于同一个分支。
16.可选的，其特征在于，将参数分支代入第二有理参数曲面中，求出三维空间中的分支。
17.可选的，其特征在于，在第一有理参数曲面中利用参数的边界以及步长求出边界点。
18.可选的，找到与边界点里的足够近的在分支上的点，把分支分为多段，对于一段来说，选择任意的一个点p0，对于方程p(s,t)＝κp0，κ为非零常数有解属于参数的定义域，那么就保留这一段，不满足的去除，其中p(s,t)表示第一有理参数曲面。
19.经由上述的技术方案可知，与现有技术相比，本发明公开提供了一种基于移动平面与矩阵计算两个有理参数曲面的交的方法，在求矩阵步骤，利用了dixon矩阵表示，在求出满足条件的参数时利用了步进法，并且在代数方法中本发明在对有理参曲面进行隐式化时，要求行列式的值，但是，在本发明的方法中是直接对矩阵进行操作，对于计算行列式而言，减少了许多计算的复杂度。
附图说明
20.为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据提供的附图获得其他的附图。
21.图1是本发明基于高斯像的可展面分割-拟合方法的总体框架流程图；
22.图2是本发明步骤s4拟合线状点集，生成对应可展面的框架流程图；
23.图3是本发明分割-拟合过程中的结果示意图；
24.图4是本发明步骤s4拟合过程中的结果示意图；
25.图5是步骤s6将分支分段的结果示意图；
26.图6a-图6b是关于例子两个环面度数为相交的计算结果图；
27.图7a-图7c是两个度数为的犹他茶壶计算交线的过程图；
28.图8a-图8b是两个度数为的犹他茶壶计算交线的结果图；
29.图9是本发明与现有其他方法在在计算不同度数有理曲面交线时间的对比结果
图。
30.图10是计算犹他茶壶面交线时我们的方法与其余经典方法所用时间的结果对比图
31.图11是本发明计算经典的一些曲面的交线的结果示意图。
具体实施方式
32.下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
33.在用cad软件等相关软件设计汽车，轮船，飞机，火车，航天飞行器等实体的外形及其部件时，会用到一些参数曲面来构造对应几何体的外形。通常情况下，并不能用单一的一张参数曲面来构造一个几何体的表面(内表面或者外表面)，而是要用到很多张参数曲面来表示这个几何体的表面。那么多张参数曲面相邻的部分就要求交，去掉无关的部分，也就是布尔运算。本发明的算法就是在这个不可或缺的环节发挥作用的。本发明的算法就是在几何体表面表示生成时，要用到本实施例的曲面求交算法。
34.本发明实施例公开了一种基于移动平面与矩阵计算有理参数曲面的交的方法，包括以下步骤：
35.通过三维扫描仪对现有产品进行扫描得到产品的网格模型；
36.根据网格模型计算出第一有理参数曲面的矩阵表示；
37.将第二有理参数曲面的参数代入第一有理参数曲面至矩阵表示中，利用步进法求出一系列参数；
38.将一系列参数分类为不同的参数分支并转化为三维空间中的分支；
39.根据第一有理参数曲面计算出的边界点将三维空间中的分支分为几段，去掉多余的段，得到参数化结果；
40.利用新的参数化结果再次进行参数曲面拟合最终得到产品模型，并利用高精度产品模型对产品进行逆向工程的制造。
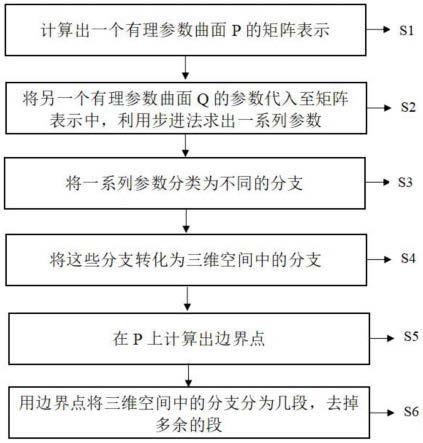
41.具体的，本实施例的具体计算过程如下：
42.步骤s1、计算出一个有理参数曲面p的矩阵表示；
43.步骤s2、将另一个有理参数曲面q的参数代入至矩阵表示中，利用步进法求出一系列参数；
44.步骤s3、将一系列参数分类为不同的分支；
45.步骤s4、将这些分支转化为三维空间中的分支；
46.步骤s5、在p上计算出边界点
47.步骤s6、用边界点将三维空间中的分支分为几段，去掉多余的段。优选的。
48.下面对上述每个步骤进行更加详细的说明。
49.步骤s1、计算出一个有理参数曲面p的矩阵表示
50.本实施例的输入是两个有理参数曲面p(s,t)且(s,t)∈[0,1]
×
[0,1]和q(u,v)且(u,v)∈[0,1]
×
[0,1]令r[s,t]是s,t生成的多项式环，p(s,t)被称为度为(m,n)的定义为p
(s,t)＝(a(s,t),b(s,t),c(s,t),d(s,t))，其中a(s,t),b(s,t),c(s,t),d(s,t)中s的次数不大于m，t的次数不大于n且它们是线性无关的，且gcd(a,b,c,d)＝1,p(s,t)称为可正确参数化的含义为再去掉有限多的点后，映射是一一映射，如果a(s0,t0)＝b(s0,t0)＝c(s0,t0)＝d(s0,t0)＝0一个参数对(s0,t0)就被称为基点，一个基点被称为局部完全交线基点(lci)的定义为理想《a,b,c,d》可以被基点领域的两个元素所生成，其余情况被称为非-lci基点。
[0051]
一个度数为(v1,v2)的移动平面的定义为一族满足下述条件的平面l(x；s,t)：＝a(s,t)x+b(s,t)y+c(s,t)z+d(s,t)w＝0，其中其中x＝(x,y,z,w)是定义在三维实射影空间上的齐次坐标，a(s,t),b(s,t),c(s,t),d(s,t)∈r[s,t]是s的最大次数为v1，t的最大次数为v2的多项式，一个被称为跟着有理曲面的移动平面的定义为l(p(s,t)；s,t)≡0，从几何的角度来看，对于每一个参数值(s,t)来说，l(x；s,t)＝0总会穿过对应的在曲面p(s,t)上的点有时候，把l(x；s,t)写成向量的形式l(s,t)＝a(s,t),b(s,t),c(s,t),d(s,t))。任意两个跟随有理曲面的移动平面混合运算依旧是有理曲面的移动平面。
[0052]
给出三个度为(m,n)的多项式给出三个度为(m,n)的多项式f(s,t),g(s,t),h(s,t)的2mn
×
2mn的dixon矩阵n(f,g,h)定义为由(f,g,h)定义为由所决定的结果，其中，该等式左侧的结果为一个多项式，提取该多项式sitjαkβ
l
,i＝0,1,
…
,m-1,j＝0,1,
…
,2n-1,k＝0,1,
…
,2m-1,l＝0,1,
…
,n-1的系数即可得到矩阵n(f,g,h)，例如，矩阵n(f,g,h)第1行第1列位置对应的元素为s0t0α0β0的系数，n(f,g,h)第1行第2列位置对应的元素为s1t0α0β0的系数。
[0053]
对于p(s,t)来说取三个多项式f(s,t)＝d(s,t)x-a(s,t)w,g(s,t)＝d(s,t)y-b(s,t)w,h(s,t)＝d(s,t)z-c(s,t)w,那么就可以找到一个2mn
×
2mn的n(f,g,h)矩阵，事实上，n(f,g,h)的每一行都是跟随p(s,t)的移动平面，若n(f,g,h)的秩为r，那么就存在矩阵u∈rr×
2mn
,v∈r
2mn
×r满足rank(u
·
n(f,g,h)
·
v)＝r,而r
×
r的矩阵就是p(s,t)的dixon矩阵表示，其中，u和v可通过生成随机矩阵来获得。如果一个有理曲面没有基点或它的隐函数表达式度数等于r，那么一个点p0＝(x0,y0,z0,w0)在曲面p(s,t)上当且仅当
[0054]
步骤s2、将另一个有理参数曲面q的参数代入至矩阵表示中，利用步进法求出一系列参数坐标点，具体的，包括如下内容：
[0055]
s21：对于(u,v)∈[0,1]
×
[0,1]，将其分为n
×
n统一的网格，之后令对于每一个方格的顶点(ui,vj)作为参数代入至为m(ui,vj)，那么令δ
ij
：＝sign(|m(ui,vj)|)；
[0056]
s22：对于每个网格，如果它的四个顶点有一个是δ
ij
＝0或者是图3中1-16种情形中的一种，那么就把这个网格再等分为四个相同的网格。
[0057]
s23：重复步骤s22k次直至网格的大小
[0058]
s24：对于每个最后产生的网格，如果有顶点δ
ij
＝0，那么这个顶点对应的参数对是符合要求的，如果网格满足图3中1-16种情形中的一种，那么选取灰线的中点对应的为满足要求的参数对，主要由于将(u,v)代入形成的|m(u,v)|是关于u,v连续的函数，如果固定u＝u0，v0《v1，如果m(u0,v0)》0并且m(u0,v1)《0，那么这里就有一个v0《v
*
《v1满足m(u0,v
*
)＝0，因此δ
ij
在顶点的符号的变化指出在网格中应该有参数对(u
*
,v
*
)满足m(u
*
,v
*
)＝0，并且由于最后选取的网格的大小，选取的参数对集合u满足与(u
*
,v
*
)的距离小于ε
[0059]
步骤s3、将(ui,vi)与(uj,vj)分类为一个分支，将u,v从小到大遍历网格，对于(ui,vi)来说，如果在已存在的分支有(uj,vj)满足(ui,vi)与(uj,vj)来自相邻的网格，称这两个在同一个分支，若(ui,vi)属于两个以上的分支，那么考虑到它所对应的点是奇点，单独储存，若不属于任意一个现有的分支，那么创造一个新的分支。
[0060]
步骤s4、将已经分类好的分支代回至q(u,v)中从而有在三维空间中的分支bj。
[0061]
步骤s5、首先在[0,1]
×
[0,1]的四个边界线上以步长1/n取样s,t，然后便得到了一系列边界点
[0062]
步骤s6、首先在步骤s2中所得到的参数对所对应的点是在本质上确定了两个曲面在(s,t)∈[-∞,+∞]
×
[-∞,+∞]和(u,v)∈[0,1]
×
[0,1]中的交点。之所以有(s,t)∈[-∞,+∞]
×
[-∞,+∞]，是因为矩阵表示本质上起着隐式化的作用，不局限于参数域。因此，下面需要进一步去掉定义域[0,1]
×
[0,1]以外的那些(s,t)。为此检查交线分支b是否与t相交，为了检验，检查点pj∈t是否与一个bi∈b离的足够近，那么将bi看作是b与t的交点的近似，并且通过bi将b分割成几部分c0,c1,
…
,c
γ
，对于一段ci,i＝1,
…
,γ来说，选择任意的一个点p0，对于方程p(s,t)＝κp0，κ为非零常数有解属于参数的定义域，那么就保留这一段，不满足的去除。
[0063]
图3展示了本发明步骤s2在把(u,v)∈[0,1]
×
[0,1]，将其分为n
×
n统一的网格，网格的顶点如果δ
ij
不为0的各种情形，而灰线的中点是满足要求的参数对。
[0064]
图4展示了本发明步骤s2中如何把网格细分，可以看到网格从大往小分，然后得到了叙述中满足要求的参数对
[0065]
图5展示了本发明步骤s6中利用边界点如何把一条交线的分支分为了几部分的结果示意图。
[0066]
图6展示了两个度数为(2,2)环面的交的求解结果，而(a)是在展示利用步骤s2中求出来的参数分支，而(b)中蓝色部分为有理曲面q(u,v)，而橙色为有理曲面p(s,t)，而灰色则是两个的交线。
[0067]
图7展示了两个度为(3,3)犹他茶壶面的交的求解过程其中(a)中的灰线是s2中计算出来的符合条件的参数对分支，而虚线对应的部分则是额外的部分(b)中的灰色的部分则是转化成三维空间中的分支，(c)中则是最后所得到的曲线。
[0068]
图8展示了两个度为(3,3)犹他茶壶面的交的求解结果，(a)是(s,t)∈[-∞,+∞]
×
[-∞,+∞]和(u,v)∈[0,1]
×
[0,1]所得到的结果，而(b)是(s,t)∈[0,1]
×
[0,1]和(u,v)∈[0,1]
×
[0,1]所得到的结果。
[0069]
图9展示了本方法与经典方法例如代数-追踪法，细分法还有rep-mν方法关于实现不同度数有理曲面相交问题的时间长短的对比很明显的，可以看到在与其他方法的对比中，本方法所花费的时间是少一些的。
[0070]
图10展示了本方法与经典方法代数-追踪法，细分法还有rep-mν方法关于实现计算不同的犹他茶壶面之间的交点所花费时间的对比，依旧本方法比其余的方法更为高效一些。
[0071]
图11则是在用本方法计算不同的经典有理曲面类似enneper surface,henneberg surface和octahedron surface这些具备复杂特性类似于自交性的曲面之间的交线。
[0072]
本发明技术方案提出了一种高效的基于移动平面与矩阵计算两个有理参数曲面交线方法。输入曲面或两曲面相交曲线上奇异点的自交往往给正确计算相交曲线带来困难。例如，代数跟踪法中的跟踪步骤通常是在一个曲面的交线或自交点的奇点附近被破坏。相反，本发明的算法对输入曲面的自交或交点曲线的自交和尖点的存在是鲁棒的。本发明的算法包括两个阶段:代数阶段给出一个曲面的矩阵表示，步进平方阶段类似于格子方法。第一阶段在很大程度上保留了输入曲面的代数性质。第二阶段在参数域的目标-得到曲线附近实现自适应细分。本发明的算法对比传统方法更具有效率，当输入曲面系数为浮点数时，本发明的算法是数值稳定的，因为该算法主要依赖于矩阵表示的计算和平方步进技术，而且这两个步骤都是数值稳定的。
[0073]
上述实验结果和计算两个有理参数曲面交线方法，可以用于边界生成，网格生成，绘制，隐藏面去除和制造等多方面，具有较高的实际应用价值。
[0074]
本说明书中各个实施例采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似部分互相参见即可。对于实施例公开的装置而言，由于其与实施例公开的方法相对应，所以描述的比较简单，相关之处参见方法部分说明即可。
[0075]
对所公开的实施例的上述说明，使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下，在其它实施例中实现。因此，本发明将不会被限制于本文所示的这些实施例，而是要符合与本文所公开的原理和新颖特点相一致的最宽的范围。