一种基于x86平台SIMD的不可约多项式及量子安全哈希值计算方法与流程

一种基于x86平台simd的不可约多项式及量子安全哈希值计算方法
技术领域
1.本发明涉及量子安全技术领域，具体涉及一种基于x86平台simd的不可约多项式及量子安全哈希值计算方法。


背景技术：

2.早期，我们在传输信息时，由于信道不安全可能会出现信息错乱，接收方需要反复多次确认来判断收发信息的一致性，而来回多次传送确认是效率极低的一种通信方式。如果利用哈希算法则可很好地解决这一问题，哈希算法是区块链中使用最多的一种算法，它被广泛地用于构建区块和确认交易的完整性上。例如，在比特币中，使用哈希算法把交易生成数据摘要，当前区块中包含上一个区块的哈希值，后面一个区块又包含当前区块的哈希值，就这样一个接一个地连接起来，形成一个不可逆向篡改的链表。
3.哈希值和哈希函数的概念对安全性来说特别关键。哈希是一种数学计算机程序，它接收任何一组任意长度的输入信息，通过哈希算法变换成固定长度的数据指纹输出形式，如字母和数字的组合，该输出就是“哈希值”。总体而言，哈希算法可以理解为一种消息摘要算法，将消息或数据压缩变小并拥有固定的格式。由于其单向运算具有一定的不可逆性，哈希算法已成为加密算法中一个构成部分。目前常见的哈希算法包括国际上的md系列和sha系列算法，以及国内的 sm3 算法。
4.而哈希算法计算哈希值的时候，最主要的就是哈希函数的生成，哈希函数的生成大部分都基于不可约多项式。专利号为cn202111360079.5，专利名称为的一种基于lfsr哈希的无条件安全的认证加密方法，该专利中提出了一种计算不可约多项式的方法，但其是一种数学思路，不能在x86平台simd上进行运用，而且根据此不可约多项式生成哈希函数计算哈希的方法在计算过程中效率低下，工程实践效果差。因此一种适用于x86平台simd且高效的不可约多项式计算方法和哈希计算方法的提出就显得尤为重要。


技术实现要素：

5.发明目的：本发明目的是提供一种基于x86平台simd的不可约多项式及量子安全哈希值计算方法，解决了目前计算不可约多项式的方法不能在x86平台simd上进行运用的问题，而且解决了根据此不可约多项式生成哈希函数计算哈希的方法在计算过程中效率低下，会耗费大量的资源的问题。本发明基于x86平台simd去计算不可约多项式，并在此基础上得到最终的哈希值，整个技术方案在时间和空间效率方面都有大幅的提升。
6.技术方案：本发明一种基于x86平台simd的不可约多项式计算方法，包括以下步骤：（1）初始化一个128位的数g，该数g分为前64位和后64位两部分，前64位的最后一位数值为1，其他位数值为0；后64位的每一位数值均为0；（2）取一个128位的随机数，并在随机数的最低位右边增加一位从而形成一个129
位的随机数，将129位随机数的最高位数值和最低位数值改为1，得到新的随机数p；（3）根据步骤（1）和步骤（2）得到的g和p，进行迭代计算得到不可约多项式中每一项系数组成的字符串，再通过不可约多项式中每一项系数组成的字符串生成不可约多项式。
7.进一步的，所述迭代计算得到不可约多项式中每一项系数组成的字符串的具体过程步骤为：1）第一次：计算数g的平方再对p进行取模运算得到数,；2）第二次：计算数的平方再对p进行取模运算得到数,；以此类推，58）第五十八次：计算数的平方再对p进行取模运算得到数,；对数进行判断：若，则随机数p为不可约多项式中每一项系数组成的字符串；若，则随机数p不是不可约多项式中每一项系数组成的字符串，此时将随机数p的二进制数值与二进制数值10相加形成新的随机数p，再利用数g和新的随机数p返回步骤1）重新计算；若不等于1也不等于2，则继续计算：59）第五十九次：计算数的平方再对p进行取模运算得到数,；60）第六十次：计算数的平方再对p进行取模运算得到数,；以此类推，122）第一百二十二次：计算数的平方再对p进行取模运算得到数,；对数进行判断：若，则随机数p不是不可约多项式中每一项系数组成的字符串，此时将随机数p的二进制数值与二进制数值10相加形成新的随机数p，再利用数g和新的随机数p返回步骤1）重新计算；若，则计算，如果，则随机数p为不可约多项式中每一项系数组成的字符串；如果，则随机数p不是不可约多项式中每一项系数组成的字符串，此时将随机数p的二进制数值与二进制数值10相加形成新的随机数p，再利用数g和新的随机数p返回步骤1）重新计算。
8.进一步的，所述数、数至数中任意一个数的平方计算过程如下：首先，令数、数至数中任意一个数为,n为1至121中的正整数；将该数
中除最低位数值外的每一位数值之后插入0从而形成该数的平方，即。
9.进一步的，所述数中除最低位数值外的每一位数值之后插入0从而形成该数的平方过程如下：（a）判断数是否为128位，若是，则进行下一步；若不是，将数的二进制数值最高位左边补0，直至形成128位的数；（b）将128位数的最低位右边补0，直至形成256位的数g；（c）64位交错：将数g均分为4部分，并使其中的第2部分二进制数值与第3部分二进制数值进行交换，形成数g1；（d）32位交错：将数g1均分为2组，将每组的二进制数值再均分为4部分，并使每组中的第2部分二进制数值与第3部分二进制数值进行交换，形成数g2；（e）16位交错：将数g2均分为4组，将每组的二进制数值再均分为4部分，并使每组中的第2部分二进制数值与第3部分二进制数值进行交换，形成数g3；（f）8位交错：将数g3均分为8组，将每组的二进制数值再均分为4部分，并使每组中的第2部分二进制数值与第3部分二进制数值进行交换，形成数g4；（g）4位交错：将数g4均分为16组，将每组的二进制数值再均分为4部分，并使每组中的第2部分二进制数值与第3部分二进制数值进行交换，形成数g5；（h）2位交错：将数g5均分为32组，将每组的二进制数值再均分为4部分，并使每组中的第2部分二进制数值与第3部分二进制数值进行交换，形成数g6；（i）1位交错：将数g6均分为64组，将每组的二进制数值再均分为4部分，并使每组中的第2部分二进制数值与第3部分二进制数值进行交换，形成数g7；（j）计算数g7的最高有效位数，将数g7的最高有效位数左边的所有二进制数值0删除，以及将数g7的最低位二进制数值0删除，形成数g8，数g8即为该数的平方。
10.进一步的，所述数、数至数中任意一个数的平方对p进行取模运算的计算过程步骤如下：s1 计算出和p的最高有效位数, 分别记为uleng和ulenb；s2 将p的二进制数值左移uleng
ꢀ‑ꢀ
ulenb位，并在低位补0得到p1；s3 将与p1进行异或，得到新的，计算新的的最高有效位数，得到 ；s4 比较 与ulenb，若 大于或等于ulenb，则将步骤s3中新的返回步骤s1，继续重复步骤s1至s3，直至 小于ulenb，则输出步骤s3中的，即为输出结果。
11.本发明还包括一种基于x86平台simd的量子安全哈希值计算方法，包括以下步骤：步骤1：将明文c均分为n份，每份为128位的数据；步骤2：取一个128位的随机数r，将随机数r的二进制数值最高位左边补0再与上述
方法得到的不可约多项式中每一项系数组成的字符串进行异或操作得到数m1，将数m1中的每一位二进制数值依次进行异或得到一位的数t1，然后将随机数r的最高位左边补上数t1，并删除随机数r的最低位二进制数值，得到一个新的128位的随机数r1；将随机数r1的二进制数值最高位左边补0再与不可约多项式中每一项系数组成的字符串进行异或操作得到数m2，将数m2中的每一位二进制数值依次进行异或得到一位的数t2，然后将随机数r1的最高位左边补上数t2，并删除随机数r1的最低位二进制数值，得到一个新的128位的随机数r2；以此类推，直至将随机数r127的二进制数值最高位左边补0再与不可约多项式中每一项系数组成的字符串进行异或操作得到数m128，将数m128中的每一位二进制数值依次进行异或得到一位的数t128，然后将随机数r127的最高位左边补上数t128，并删除随机数r127的最低位二进制数值，得到一个新的128位的随机数r128；步骤3：构建128
×
128的矩阵，该矩阵的第一列数值为随机数r1且随机数r1的最高位位于矩阵的第128行，第二列数值为随机数r2且随机数r2的最高位位于矩阵的第128行，以此类推，第一百二十八列数值为随机数r128且随机数r128的最高位位于矩阵的第128行，从而形成矩阵q1；步骤4：将随机数r128作为新的随机数r代替步骤2中的随机数r，重复步骤2和步骤3得到矩阵q2；以此类推，直至得到矩阵qm，m与n相同；步骤5：将矩阵q1和明文c中的第一份128位数据对应的列向量进行异或乘操作或与判断操作得到第一哈希值h1，将矩阵q2和明文c中的第二份128位数据对应的列向量进行异或乘操作或与判断操作得到第二哈希值h2，以此类推，将矩阵qm和明文c中的第n份128位数据对应的列向量进行异或乘操作或与判断操作得到第n哈希值hx；步骤6：最后将第一哈希值h1、第二哈希值h2直至第n哈希值hx依次进行异或得到哈希值f，哈希值f即为明文c的量子哈希值。
12.进一步的，所述异或乘操作具体过程步骤如下：a1：将参与异或乘操作的矩阵表示为，将参与异或乘操作的明文c中的128位数据对应的列向量表示为；a2：取矩阵的第一行异或乘明文c中的128位数据对应的列向量，得到第一个二进制数值z1，即；a3：取矩阵的第二行异或乘明文c中的128位数据对应的列向量，得到第二个二进制数值z2，即；a4：以此类推，直至取矩阵的第一百二十八行异或乘明文c中的128位数据对应的列向量，得到第一百二十八个二进制数值z128，即；
a5：将第一个二进制数值z1、第二个二进制数值z2直至第一百二十八个二进制数值z128按顺序组成数值串，则得到对应的哈希值。
13.进一步的，所述与判断操作具体过程步骤如下：b1：将参与与判断操作的矩阵表示为，将参与与判断操作的明文c中的128位数据对应的列向量表示为；b2：取矩阵的第一行与明文c中的128位数据对应的列向量进行逻辑与运算，得到数w1，即，再判断数w1中1的个数，如果1的个数为奇数，则输出结果为1；如果1的个数为偶数，则输出结果为0；最终将输出结果记为第一个二进制数值z1；b3：取矩阵的第二行与明文c中的128位数据对应的列向量进行逻辑与运算，得到数w2，即，再判断数w2中1的个数，如果1的个数为奇数，则输出结果为1；如果1的个数为偶数，则输出结果为0；最终将输出结果记为第一个二进制数值z2；b4：以此类推，直至取矩阵的第一百二十八行与明文c中的128位数据对应的列向量进行逻辑与运算，得到数w128，再判断数w128中1的个数，如果1的个数为奇数，则输出结果为1；如果1的个数为偶数，则输出结果为0；最终将输出结果记为第一个二进制数值z128；b5：将第一个二进制数值z1、第二个二进制数值z2直至第一百二十八个二进制数值z128按顺序组成数值串，则得到对应的哈希值。
14.本发明的有益效果：本发明相较于现有技术，能够基于x86平台simd去计算不可约多项式，并在此基础上得到最终的哈希值，整个技术方案在时间和空间效率方面均有大幅的提升；而且在二进制的平方运算过程中，采用交错法实现平方运算，相较于传统循环移位的实现，效率提升4倍以上；在量子哈希计算过程中，采用异或乘操作或与判断操作进行哈希运算，其中与判断操作运算效率高，使得哈希计算的效率也得到了提升。
附图说明
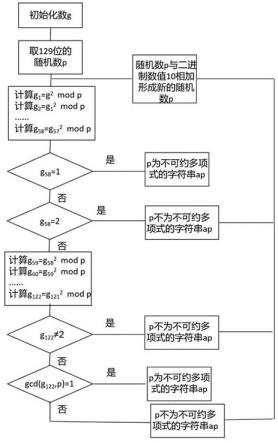
15.图1为数g的示意图；图2为随机数p的示意图；图3为求不可约多项式流程图；图4为通用寄存器拆分为64bit存储数据示意图；图5为数组存储多项式示意图；图6为packed和scalar加法运算示意图。
具体实施方式
16.下面结合附图和实施例对本发明做进一步描述：本发明在计算哈希值的时候，首先对于给定的随机数，求解一个不可约多项式，然后再用lfsr的方式对一个新的随机数进行变换得到矩阵，然后利用变化出来的矩阵与待哈希的明文一段一段进行异或乘操作或与判断操作，最终将一段一段的128bit的哈希值，互相再进行异或操作，得到最终的哈希。
17.简单说分成两步：第一步计算不可约多项式；第二步利用lfsr根据第一步得到的不可约多项式计算哈希值。
18.本发明提出了一种基于x86平台simd的不可约多项式计算方法，包括以下步骤：（1）初始化一个128位的数g，数g的格式要求如图1所示，该数g分为前64位和后64位两部分，前64位的最后一位数值为1，其他位数值为0；后64位的每一位数值均为0；（2）取一个128位的随机数，并在随机数的最低位右边增加一位从而形成一个129位的随机数，将129位随机数的最高位数值和最低位数值改为1，得到新的随机数p，p的结构如图2所示；（3）根据步骤（1）和步骤（2）得到的g和p，进行迭代计算得到不可约多项式中每一项系数组成的字符串，再通过不可约多项式中每一项系数组成的字符串生成不可约多项式。
19.如图3所示，迭代计算得到不可约多项式中每一项系数组成的字符串的具体过程步骤为：1）第一次：计算数g的平方再对p进行取模运算得到数,；2）第二次：计算数的平方再对p进行取模运算得到数,；以此类推，58）第五十八次：计算数的平方再对p进行取模运算得到数,；对数进行判断：若，即，则此时可以证明随机数p为不可约多项式中每一项系数组成的字符串；若，则说明随机数p不是不可约多项式中每一项系数组成的字符串，需从头开始重新计算，此时将随机数p的二进制数值与二进制数值10相加形成新的随机数p，再利用数g和新的随机数p返回步骤1）重新计算；若不等于1也不等于2，则继续计算：59）第五十九次：计算数的平方再对p进行取模运算得到数,；60）第六十次：计算数的平方再对p进行取模运算得到数,；以此类推，122）第一百二十二次：计算数的平方再对p进行取模运算得到数,
；对数进行判断：若，则随机数p不是不可约多项式中每一项系数组成的字符串，此时将随机数p的二进制数值与二进制数值10相加形成新的随机数p，再利用数g和新的随机数p返回步骤1）重新计算；若，即，则计算p与相互取模的结果即计算，如果，则随机数p为不可约多项式中每一项系数组成的字符串；如果，则随机数p不是不可约多项式中每一项系数组成的字符串，此时将随机数p的二进制数值与二进制数值10相加形成新的随机数p，再利用数g和新的随机数p返回步骤1）重新计算。
20.涉及到计算，而g和p都不是小数字，直接算的话，有两种方法：方法一：通用寄存器只能存储64位的数据，所以把128位的数据分成两个64位数据存储。平方操作后128位的数据最大不会超过256位数据，所以需要有四个64位去存储数据，然后再对这个数据进行移位，二进制模等运算，如图4所示；方法二：把128位的数据存储在一个数组array里，如图5所示。
21.以上这两种方法都存在一定的问题。第一种方法，首先由于计算过程中会经常用到256位的数据来求解不可约多项式，因此两个64位的数就会在需要的时候，变成四个64位的数；其次，不管是针对两个64位的数还是四个64位的数，我们需要实现各种移位、二进制模、加法等运算，需要区分高低位运算，同时还涉及到进位、退位等，每实现一个算子，都相当复杂。第二种方法，用数组的方式存储数据进行运算，这种方法的优点就是可以支持更高维的计算，例如如果需要计算512位，甚至1024位，再大都能平行扩展。但是第一种方法存在的问题，在第二种方法上统统都存在，例如加减乘除，需要进位借位，因为是数组中的元素，所以这些操作都是跨字节的，因此在时间和空间上效率更低。
22.本发明采用一种新的方法，利用simd指令集，充分发挥平行计算的优势，结合本发明优化的计算方法，经过测试，性能提升到几乎和硬件计算效率差不多，例：fpga（注：一种可编程的半定制电路）。求解不可约多项式的性能：采用传统运算的方式，优化前：900ms/个，优化后：约合2.2ms/个；利用lfsr计算哈希，优化前17mb/s，优化后100mb/s。目前支持sse指令集的cpu，其xmm寄存器是可以存储128位数据，而支持avx/avx2指令集的cpu，其ymm寄存器可以一次性装载256位数据，这就为本发明的运算提供了极大的操作空间和效率提升空间。
23.simd指令集的运算指令分为两大类：packed和scalar。如图6所示，packed指令是一次对xmm寄存器中的四个数，即data0 ~ data3，均进行计算，而scalar则只对xmm寄存器中的data0进行计算。例如对128位数据做算术运算和逻辑运算，用scalar的方式实现，这里以加法为例，步骤是这样的：先计算a0 + b0；再计算a1 + b1，然后进位；进而计算a2 + b2，然后进位；最后计算a3 + b3，然后进位，才完成一次完整的加法运算。而用packed方式，则只需要调用诸如：_mm_add_epi32这类加法指令即可完成加法运算。所以packed方式大量减
少了循环和比较，是本发明采取的方式。
24.在此基础上，由上可知是一个128位的数据，128位的数据平方后得到的结果最大不会超过256位，所以本发明利用simd寄存器，并且当前计算机支持avx指令。使用支持sse指令集的cpu中的xmm寄存器来存储128位的数据，用avx指令集的ymm寄存器来存储最大不会超过256位的平方后的结果。知道如何对数据做存储后，我们再来计算。
25.其中，数、数至数中任意一个数的平方计算过程如下：首先，令数、数至数中任意一个数为,n为1至121中的正整数；将该数中除最低位数值外的每一位数值之后插入0从而形成该数的平方，即。举例说明：举一些常规二进制平方的例子，例如；；；从这些例子中，可以发现一个规律，即二进制的数据平方后就是在原有数值之间插入0。
26.实现插0，可以通过不停移位的方法做到，但是移位的方法计算量大，所以本发明采用交错实现，即数中除最低位数值外的每一位数值之后插入0从而形成该数的平方过程如下：（a）判断数是否为128位，若是，则进行下一步；若不是，将数的二进制数值最高位左边补0，直至形成128位的数；（b）将128位数的最低位右边补0，直至形成256位的数g；（c）64位交错：将数g均分为4部分，并使其中的第2部分二进制数值与第3部分二进制数值进行交换，形成数g1；（d）32位交错：将数g1均分为2组，将每组的二进制数值再均分为4部分，并使每组中的第2部分二进制数值与第3部分二进制数值进行交换，形成数g2；（e）16位交错：将数g2均分为4组，将每组的二进制数值再均分为4部分，并使每组中的第2部分二进制数值与第3部分二进制数值进行交换，形成数g3；（f）8位交错：将数g3均分为8组，将每组的二进制数值再均分为4部分，并使每组中的第2部分二进制数值与第3部分二进制数值进行交换，形成数g4；（g）4位交错：将数g4均分为16组，将每组的二进制数值再均分为4部分，并使每组中的第2部分二进制数值与第3部分二进制数值进行交换，形成数g5；（h）2位交错：将数g5均分为32组，将每组的二进制数值再均分为4部分，并使每组中的第2部分二进制数值与第3部分二进制数值进行交换，形成数g6；（i）1位交错：将数g6均分为64组，将每组的二进制数值再均分为4部分，并使每组中的第2部分二进制数值与第3部分二进制数值进行交换，形成数g7；（j）计算数g7的最高有效位数，将数g7的最高有效位数左边的所有二进制数值0删除，以及将数g7的最低位二进制数值0删除，形成数g8，数g8即为该数的平方。
27.举例：一次操作128位的数据，由于128位的数据太长，版面影响，故以16位的数据来具体说明交错；
首先将16位的数据最低位右边补0，直至形成32位的数据；1、交错：均分为4部分，并使其中的第2部分二进制数值与第3部分二进制数值进行交换；交错前：abcd efgh ijkl mnop 0000 0000 0000 0000；交错后：abcd efgh 0000 0000 ijkl mnop 0000 0000；2、交错：先均分为2组，将每组的二进制数值再均分为4部分，并使每组中的第2部分二进制数值与第3部分二进制数值进行交换；交错前：abcd efgh 0000 0000 ijkl mnop 0000 0000；交错后：abcd 0000 efgh 0000 ijkl 0000 mnop 0000；3、交错：先均分为4组，将每组的二进制数值再均分为4部分，并使每组中的第2部分二进制数值与第3部分二进制数值进行交换；交错前：abcd 0000 efgh 0000 ijkl 0000 mnop 0000；交错后：ab00 cd00 ef00 gh00 ij00 kl00 mn00 op00；4、交错：先均分为8组，将每组的二进制数值再均分为4部分，并使每组中的第2部分二进制数值与第3部分二进制数值进行交换；交错前：ab00 cd00 ef00 gh00 ij00 kl00 mn00 op00；交错后：a0b0 c0d0 e0f0 g0h0 i0j0 k0l0 m0n0 o0p0；（由于数值是16位的，所以交错4次即可，而128位的数值需要按上述方法继续交错，直至形成数的平方）然后将最高有效位数左边的所有二进制数值0删除，以及将最低位二进制数值0删除，至此，得到了交错后的结果；完成了16位数据的插0运算，也就是实现了二进制的平方运算，数也是同理，首先将数的二进制数值最高位左边补0，直至形成128位；将128位数的最低位右边补0，直至形成256位的数g，再进行交错直至形成最终的数的平方。经过测算，该算法相较于传统循环移位的实现，效率提升4倍以上，在部分高主频的机器上甚至能达到8倍以上。
28.利用simd单指令多数据的方式，一个指令周期内就可以操作128位、256位，甚至512位的数据，当数的平方得到之后，数的平方对p进行取模运算的计算过程步骤如下：s1 计算出和p的最高有效位数, 分别记为uleng和ulenb；s2 将p的二进制数值左移uleng
ꢀ‑ꢀ
ulenb位，并在低位补0得到p1；这一步实际上仅仅就是将p低位补0，在总长度上与对齐；s3 经过上一步之后，与p1的总长度是相等的，将与p1进行异或，得到新的，计算新的的最高有效位数，得到 ；s4 比较 与ulenb，若 大于或等于ulenb，则将步骤s3中新的返回步骤s1，继续重复步骤s1至s3，直至 小于ulenb，则输出步骤s3中的，
即为输出结果。整个计算过程，简单说就是不停把p进行移位，异或掉最高位，直到新的的最高有效位数小于p的最高有效位数。
29.综上，实现了的高效运算，进而判断出了p是不是不可约多项式中每一项系数组成的字符串。
30.量子哈希运算经常会使用到线性反馈移位寄存器来与明文进行运算。线性反馈移位寄存器，下文简称为lfsr,是指将前一状态输出的线性函数再用作输入的移位寄存器。异或运算是最常见的单比特线性函数：对寄存器的某些比特位进行异或操作后作为输入，再对寄存器中的各比特进行整体移位。lfsr在工程实现中大都基于硬件来操作，如果是用软件的方式来计算lfsr，时间和空间上都会很复杂，本发明提出一种基于x86平台simd的量子安全哈希值计算方法，包括以下步骤：步骤1：将明文c均分为n份，每份为128位的数据；步骤2：取一个128位的随机数r，将随机数r的二进制数值最高位左边补0（变成129位）再与上述方法得到的不可约多项式中每一项系数组成的字符串（129位）进行异或操作得到数m1，将数m1中的每一位二进制数值依次进行异或得到一位的数t1，然后将随机数r的最高位左边补上数t1，并删除随机数r的最低位二进制数值，得到一个新的128位的随机数r1；将随机数r1的二进制数值最高位左边补0再与不可约多项式中每一项系数组成的字符串进行异或操作得到数m2，将数m2中的每一位二进制数值依次进行异或得到一位的数t2，然后将随机数r1的最高位左边补上数t2，并删除随机数r1的最低位二进制数值，得到一个新的128位的随机数r2；以此类推，直至将随机数r127的二进制数值最高位左边补0再与不可约多项式中每一项系数组成的字符串进行异或操作得到数m128，将数m128中的每一位二进制数值依次进行异或得到一位的数t128，然后将随机数r127的最高位左边补上数t128，并删除随机数r127的最低位二进制数值，得到一个新的128位的随机数r128；步骤3：构建128
×
128的矩阵，该矩阵的第一列数值为随机数r1且随机数r1的最高位位于矩阵的第128行，第二列数值为随机数r2且随机数r2的最高位位于矩阵的第128行，以此类推，第一百二十八列数值为随机数r128且随机数r128的最高位位于矩阵的第128行，从而形成矩阵q1；步骤4：将随机数r128作为新的随机数r代替步骤2中的随机数r，重复步骤2和步骤3得到矩阵q2；以此类推，直至得到矩阵qm，m与n相同；步骤5：将矩阵q1和明文c中的第一份128位数据对应的列向量进行异或乘操作或与判断操作得到第一哈希值h1，将矩阵q2和明文c中的第二份128位数据对应的列向量进行异或乘操作或与判断操作得到第二哈希值h2，以此类推，将矩阵qm和明文c中的第n份128位数据对应的列向量进行异或乘操作或与判断操作得到第n哈希值hx；步骤6：最后将第一哈希值h1、第二哈希值h2直至第n哈希值hx依次进行异或得到哈希值f，哈希值f即为明文c的量子哈希值。
31.其中，异或乘操作具体过程步骤如下：
a1：将参与异或乘操作的矩阵表示为，将参与异或乘操作的明文c中的128位数据对应的列向量表示为；a2：取矩阵的第一行异或乘明文c中的128位数据对应的列向量，得到第一个二进制数值z1，即；a3：取矩阵的第二行异或乘明文c中的128位数据对应的列向量，得到第二个二进制数值z2，即；a4：以此类推，直至取矩阵的第一百二十八行异或乘明文c中的128位数据对应的列向量，得到第一百二十八个二进制数值z128，即；a5：将第一个二进制数值z1、第二个二进制数值z2直至第一百二十八个二进制数值z128按顺序组成数值串，则得到对应的哈希值。
32.与判断操作具体过程步骤如下：b1：将参与与判断操作的矩阵表示为，将参与与判断操作的明文c中的128位数据对应的列向量表示为；b2：取矩阵的第一行与明文c中的128位数据对应的列向量进行逻辑与运算，得到数w1，即，再判断数w1中1的个数，如果1的个数为奇数，则输出结果为1；如果1的个数为偶数，则输出结果为0；最终将输出结果记为第一个二进制数值z1；b3：取矩阵的第二行与明文c中的128位数据对应的列向量进行逻辑与运算，得到数w2，即，再判断数w2中1的个数，如果1的个数为奇数，则输出结果为1；如果1的个数为偶数，则输出结果为0；最终将输出结果记为第一个二进制数值z2；b4：以此类推，直至取矩阵的第一百二十八行与明文c中的128位数据对应的列向量进行逻辑与运算，得到数w128，再判断数w128中1的个数，如果1的个数为奇数，则输出结果为1；如果1的个数为偶数，则输出结果为0；最终将输出结果记为第一个二进制数值z128；b5：将第一个二进制数值z1、第二个二进制数值z2直至第一百二十八个二进制数值z128按顺序组成数值串，则得到对应的哈希值。与判断操作运算效率高于异或乘操作的效率。
33.在计算哈希的时候，这个过程是进行了128次的异或乘，异或乘涉及了大量的乘法运算，，，，刚好逻辑与运算也是这个结果：，，，，由于逻辑与运算效率比乘法运算高，所以这里本发明将乘运算更换为逻辑与运算，提升了效率。
34.乘法运算之后需要将数据进行异或操作，根据异或规律，，， ，，可知0与任何数异或都是这个数本身，1与任何数异或都是这个数的相反数。那么对于求取数据异或的值，就等价于求数据中1的个数，如果个数为奇数，则结果为1。如果个数为偶数，则结果为0。因此，我们可以把求异或，转化为求取1的个数。这样显然效率又得到了提高。
35.本发明能够基于x86平台simd去计算不可约多项式，并在此基础上得到最终的哈希值，整个技术方案在时间和空间效率方面均有大幅的提升；而且在二进制的平方运算过程中，采用交错法实现平方运算，相较于传统循环移位的实现，效率提升4倍以上；在量子哈希计算过程中，采用异或乘操作或与判断操作进行哈希运算，使得哈希计算的效率也得到了提升。