最优影响因子智能集成降尺度预测技术的制作方法

1.本发明涉及气候预测领域，尤其涉及最优影响因子智能集成降尺度预测技术。


背景技术：

2.在全球变暖背景，极端气候事件频发给人类带来的挑战，加强气象预报预测，及早未雨绸缪，是应对气候变化的重要举措。气候预测指的是对延伸期(11天到30天)、月、季节和年度的气候趋势进行预测，是国家各级政府气象灾害防御、社会各界物资配置、流域水资源调配、农业生产安排等决策的重要科学依据，在国民经济和社会发展中发挥着极其重要的作用。然而截止目前，气候预测的理论、方法和实践尚不成熟，气候预测还存在很大的不确定性，仍是当前世界大气科学领域的难题。整体来看气候预测仍处于研究、试验和业务应用不断改进的阶段。
3.随着气候预测模式的发展，模式的预测要素越来越多，仅大气环流的预测结果就达到十数层或者数十层，其中包括位势高度、风场、垂直速度、湿度、温度等要素。庞大的数据给气候预测带来了新的利好，但利用传统降尺度预测方法，寻找有效的物理统计预测因子，建立稳定的物理统计关系，则需要耗费大量人力物力，无法真正做到高效、有效的利用现有的模式数据。与此同时，很多降尺度预测方案默认模式对大气环流预测的正确，但事实上，模式对大气环流仍然存在预测误差。另一方面，人工智能等新型方法尽管在大数据挖掘计算、自学习方面有强大优势，但其对计算硬件要求高，且自学习过程尚不能得到很好的物理解释。


技术实现要素：

4.本发明的目的是为了解决现有技术中存在的缺点，如：模式的预测要素越来越多，若利用传统降尺度预测方法寻找有效的物理统计预测因子和建立稳定的物理统计关系，需要耗费大量人力物力，无法真正做到高效、有效地利用现有的模式数据。人工智能等新型方法对计算硬件要求高，建模过程为黑匣子，无法解释物理机制等。从而提出的最优影响因子智能集成降尺度预测技术。
5.为了实现上述目的，本发明采用了如下技术方案：
6.最优影响因子智能集成降尺度预测技术，包括以下步骤。
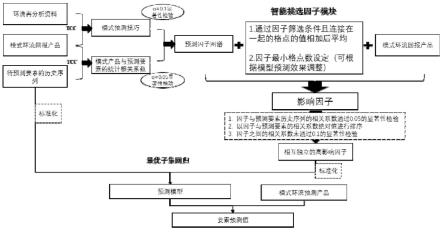
7.s1,检验模式预测产品对环流的预测技巧：采用时间长度、水平空间分辨率和垂直空间分辨率一一对应的模式回报数据和再分析数据，利用时间相关系数(tcc)检验评估模式产品对各层环流要素的预测技巧，以显著性水平α≤0.1为标准选出高预测技巧区。
8.s2,寻找模式产品与预测要素的高相关区：采用时间长度一致的模式回报数据和待预测要素历史序列，利用时间相关系数(tcc)计算模式各层环流与预测要素之间的历史统计关系，以显著性水平α≤0.05为标准选出高影响区。
9.s3,结合s1和s2步的筛选条件，构建要素的预测因子图谱
10.s4,根据预测因子图谱智能挑选影响因子：
11.①
将通过筛选条件且连接在一起的格点值相加后平均
12.②
设定因子最小格点数
13.s5,考虑到多格点平均值与要素之间统计关系的稳定性，多因子之间的关联性造成预测模型对个别因子权重倾斜的问题，采用以下步骤挑选相互独立的高影响因子：
14.①
利用时间相关系数(tcc)计算影响因子与预测要素之间的历史统计关系，以显著性水平α≤0.05为标准选出高影响因子。
15.②
以因子与预测要素相关系数的绝对值进行排序。
16.③
计算因子之间的相关系数(tcc)，以未通过0.1显著性检验为标准，检验因子之间的独立性。
17.④
选取彼此独立，且与预测要素的相关系数绝对值最高的因子
18.s6,对预测因子和待预测要素进行标准化处理。
19.s7,采用最优子集回归，确定预测要素的最优高影响因子，并构建预测要素的降尺度预测模型。
20.结合环流预测产品，得到要素预测值。
21.与现有技术相比，本发明的有益效果是：
22.(1)实现了统计降尺度转换函数建立过程中，在数十层环流场中智能挑选统计预测因子。解决了之前统计降尺度预测模型建立过程中仅用一层或者几层环流场，没有尽可能利用现有模式产品资源的现状，同时也解决了人为挑选因子的问题。
23.(2)人工智能等机器学习方法尽管能够实现大数据挖掘和机器自学习，但其建模过程为黑匣子，无法解释物理机制。与此同时，人工智能方法对计算机硬件和存储要求极高，不是每个机构或者单位都能满足；与人工智能方法相比，本技术计算量不大，可以在个人pc机上运行；实现了预测因子的智能挑选以及降尺度预测模型的建立；预测因子同时满足与预测要素高相关和模式高预测技巧两个条件，在物理机制上更容易解释。
附图说明
24.图1为本发明提出的最优影响因子智能集成降尺度预测技术的产品结构示意图；
25.图2～17为该技术用于四川省夏季降水预测的实例分析及预测效果图：
26.图2为四川省148站夏季降水聚类分型结果图；
27.图3为15个代表站点的分析图；
28.图4为四川省夏季降水代表站前3模态图；
29.图5为前三个模态建模的潜在预测技巧；
30.图6为pc1与bcc_cpsv3.0环流的相关系数图；
31.图7为pc2与bcc_cpsv3.0环流的相关系数图；
32.图8为pc3与bcc_cpsv3.0环流的相关系数图；
33.图9为pc1的高预测技巧环流影响区域图；
34.图10为pc2的高预测技巧环流影响区域图；
35.图11为pc3的高预测技巧环流影响区域图；
36.图12为pc1的相互独立的高影响因子、最优因子、预测方程和预测结果图；
37.图13为pc2的相互独立的高影响因子、最优因子、预测方程和预测结果图；
38.图14为pc3的相互独立的高影响因子、最优因子、预测方程和预测结果图；
39.图15为pc系数预测检验图；
40.图16为四川夏季降水降尺度预测模型acc预测技巧图；
41.图17为bcc_cpsv3.0降水预测产品对四川夏季降水的acc预测技巧；
42.图18～20为该技术用于四川省夏季总降水量预测的实例分析及预测效果图：
43.图18为四川夏季总降水量的高预测技巧环流影响区域图；
44.图19为四川夏季总降水量的相互独立高影响因子图；
45.图20为四川夏季区域平均降水量降尺度预测模型预测技巧图。
具体实施方式
46.下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述。显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。
47.在本发明的描述中，需要理解的是，术语“上”、“下”、“前”、“后”、“左”、“右”、“顶”、“底”、“内”、“外”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此不能理解为对本发明的限制。
48.参照图1，最优影响因子智能集成降尺度预测技术，包括以下步骤：s1,检验模式预测产品对环流的预测技巧：采用时间长度、水平空间分辨率和垂直空间分辨率一一对应的模式回报数据和再分析数据，利用时间相关系数(tcc)检验评估模式产品对各层环流要素的预测技巧，以显著性水平α≤0.1为标准选出高预测技巧区。
49.s2,寻找模式产品与预测要素的高相关区：采用时间长度一致的模式回报数据和待预测要素历史序列，利用时间相关系数(tcc)计算模式各层环流与预测要素之间的历史统计关系，以显著性水平α≤0.05为标准选出高影响区。
50.s3,结合s1和s2步的筛选条件，构建要素的预测因子图谱
51.s4,根据预测因子图谱智能挑选影响因子：
52.①
将通过筛选条件且连接在一起的格点值相加后平均
53.②
设定因子最小格点数
54.s5,考虑到多格点平均值与要素之间统计关系的稳定性，多因子之间的关联性造成预测模型对个别因子权重倾斜的问题，采用以下步骤挑选相互独立的高影响因子：
55.①
利用时间相关系数(tcc)计算影响因子与预测要素之间的历史统计关系，以显著性水平α≤0.05为标准选出高影响因子。
56.②
以因子与预测要素相关系数的绝对值进行排序。
57.③
计算因子之间的相关系数(tcc)，以未通过0.1显著性检验为标准，检验因子之间的独立性。
58.④
选取彼此独立，且与预测要素的相关系数绝对值最高的因子
59.s6,对预测因子和待预测要素进行标准化处理
60.s7,采用最优子集回归，确定预测要素的最优高影响因子，并构建预测要素的降尺度预测模型。
61.结合环流预测产品，得到要素预测值。
62.实列一：四川省夏季降水预测模型(图2～17)
63.在利用降尺度预测技术建立区域要素预测模型时，通常可用经验正交函数(eof)、典型相关分析等方法得到区域要素的主要模态，并利用其主成分与大尺度预报因子建立回归模型，最后利用空间模态与主成分对预报场进行还原。为此，将经验正交分解方法和本技术结合，构建四川夏季降水降尺度预测模型。
64.资料：采用2001～2020年cpsv3.0模式数据hgt，u，v(水平分辨率0.5
×
0.5
°
，垂直分辨率：17层)，ω(水平分辨率0.5
×
0.5
°
，垂直分辨率：12层)；采用2001～2020年cra再分析资料hgt，u，v(水平分辨率0.5
×
0.5
°
，垂直分辨率：17层)，ω(水平分辨率0.5
×
0.5
°
，垂直分辨率：12层)；1991～2020年四川省148个气象站点夏季降水资料。
65.方法：首先利用系统聚类(逐步并进)方法，对1991～2020年四川省148个气象站点夏季降水资料进行聚类分析，选择代表站点。利用经验正交分解方法对代表站点1991～2020年的夏季降水进行时空分解，选取主模态。利用“最优影响因子智能集成降尺度预测技术”建立主模态pc系数的预测方程。然后利用经验正交分解时空重建方法，建立四川省夏季降水降尺度预测模型。
66.图2为四川省1991～2020年148个气象站点夏季降水资料聚类分型结果，总体分为15类。根据分区结果，选定了15个代表站，包含3个基准站(一个地市州站)、2个地市州代表站、10个基本站。站名分别为阿坝、九寨沟、理县、剑阁、温江、蓬安、隆昌、合江、乐山、雅安、宝兴、甘洛、德昌、稻城和甘孜(图3)。
67.经过经验正交分解，代表站夏季降水的前三个模态累计方差贡献率为70％，基本囊括了四川省夏季降水的主要变化特征。第1模态呈现全区一致型，第2模态为南北反向分布，第3模态呈“川”字型分布(图4)。
68.图5为前3个模态建模后的预测潜力(acc)。若这3个模态完全预测正确的情况下，acc均值为0.39，仅一年小于0。空间分型的潜在技巧高于时下四川省夏季降水预测水平。
69.图6～8为前三个模态pc系数与bcc_cpsv3.0模式环流的相关系数分布。
70.叠加bcc_cpsv3.0的高预测技巧区域，得到前三个模态pc系数的高预测技巧影响区域，如图9～11所示。
71.根据高预测技巧影响区，并以最小格点数量为参数确定影响因子，进行回报试验发现数值设为3时预测效果最好。
72.将最小格点数设置为3得到各pc系数的影响因子，其中pc1有1257个，pc2有1200个，pc3有2853个。进而确定相互独立的高影响因子，最终得到各pc系数的最优因子、预测方程和预测结果(图12～14)。
73.由图15可以看出，依据“最优影响因子智能集成降尺度预测技术”所建立的pc系数预测方程，预测系数有非常好的拟合度，三个pc预测值与观测值的tcc分别是0.97，0.98，0.93，通过0.001的显著性水平检验。说明“最优影响因子智能集成降尺度预测技术”确定的最优预测因子和预测方程对各pc系数有非常好的预测性能。
74.经过经验正交分解时空重建建立的四川夏季降水降尺度预测模型，其平均acc为0.35，有2年的acc低于0，65％的年份acc大于0.2，最高可达0.88，对降水的空间分布有较好的预测技巧。与模式产品本身对四川省夏季降水的预测准确率(50％的年份acc小于0，平均acc为0.056)(图17)相比，有明显的提高。
75.实列二：四川省夏季总降水量预测模型
76.资料：采用2001～2021年cpsv3.0模式数据hgt，u，v(水平分辨率0.5
×
0.5
°
，垂直分辨率：17层)；ω(水平分辨率0.5
×
0.5
°
，垂直分辨率：12层)；采用2001～2021年cra再分析资料hgt，u，v(水平分辨率0.5
×
0.5
°
，垂直分辨率：17层)，omega(水平分辨率0.5
×
0.5
°
，垂直分辨率：12层)；2001～2021年四川省夏季区域平均降水量资料。
77.方法：利用“最优影响因子智能集成降尺度预测技术”建立基于bcc_cpsv3.0模式产品的夏季降水量降尺度预测模型。
78.图18为四川夏季区域平均降水量在bcc_cpsv3.0环流模式产品中的高预测技巧影响区域。根据高预测技巧影响区，并设置预测因子最小格点数为10。得到970个影响因子，经过因子独立性检验后得到9个相互独立的高影响因子(图19)，最后确立8个最优影响因子。
79.所建立的预测模型预测技巧检验结果如图20所示，在建模时段内降水量观测值与预测值的时间相关系数达到0.99，通过显著性水平为0.0001的显著性检验，误差仅为0.05％，高度拟合。对2021年做独立预测检验，绝对误差仅19.6mm，相对误差为3.4％。预测技巧较高，具有业务参考价值。
80.本发明中，首先采用时间长度、水平空间分辨率和垂直空间分辨率一一对应的模式回报数据和再分析数据，利用时间相关系数对模式各层环流要素的预测技巧进行检验评估；接下来采用时间长度一致的模式回报数据和待预测要素历史序列，利用时间相关系数计算模式各层环流与预测要素之间的历史统计关系；基于两者的结果构建要素的预测因子图谱；再根据预测因子图谱智能挑选影响因子；影响因子挑选完成后，对这些影响因子进行二次筛选，选取出彼此独立，且与预测要素的相关系数绝对值最高的因子；然后对预测因子和待预测要素进行标准化处理，采用最优子集回归，确定预测要素的最优高影响因子，并构建预测要素的降尺度预测模型；采用环流预测产品，基于所构建的预测模型得到要素预测值，根据预测值即可对气候进行预测。
81.以上所述，仅为本发明较佳的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，根据本发明的技术方案及其发明构思加以等同替换或改变，都应涵盖在本发明的保护范围之内。