一种垂直顶升法施工全过程的顶升力预测方法

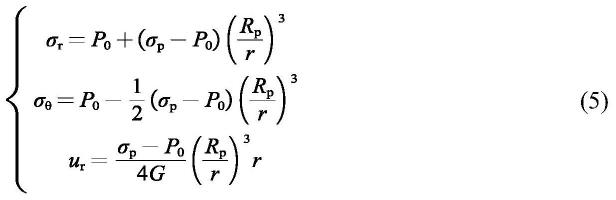
1.本发明属于地下隧道工程技术领域，涉及一种垂直顶升法施工全过程中顶升力的预测方法。


背景技术：

2.随着我国经济快速增长，沿海地区大型火力发电厂、核电厂等取排水工程也随之增加，不仅如此，城市管廊等地下工程建设往往会遇到通风及检修竖井等诸多施工问题，此背景下，垂直顶升法因其工期短、对环境影响小及效益高等优点被广泛应用。
3.在垂直顶升法施工中，顶升力的确定尤为重要，特别是对最大顶升力的确定，它不仅关系到顶升的可行性、水平隧道的稳定性，同时涉及到顶升管节的设计、隧道底部的加固以及是否需要对上部土体挖除减阻等措施。当顶升力过大时，可能造成顶升立管变形开裂及水平隧道失稳，当顶升力过小时，会无法顶升，因此有必要对垂直顶升法的顶升力进行系统性的研究。然而目前对顶升力的计算及顶升力的动态变化规律的研究较少。
4.国内外对垂直顶升法的研究大都围绕其施工工艺、止水措施，有关顶升力的计算多以经验为主，理论性不强。目前主要有两种方式计算顶升力，一种是王寿生等提出的，假定剪切破坏线顶端按1.2d～1.5d(d为立管外径)计算，顶升力由五个部分组成：水重、破坏线内土重、顶管自重、管土之间剪切力以及顶升过程中的摩擦力；另一种是上海市顶管工程施工规范
2.推荐的经验算法，给出了最大顶升力的计算公式，认为顶升首节管节时，顶升力最大，其中破土力被认为是影响顶升力的最大组成部分，针对砂土和粘土分别给出了经验取值。上述方法的不足之处有：
5.1)实际工程案例中，最大顶升力并不发生在初顶时，一般发生在顶升过程中；
6.2)王寿生算法里取值具体是采用1.2还是1.5未说明；
7.3)多为经验取值，理论性稍有不足。
8.垂直顶升法中立管不断向上顶升，土体对其的阻碍作用也在不断发生变化，因而顶升力是动态变化的。因此，根据其施工特点，需要考虑上覆土厚度的变化，重新提出一种垂直顶升法施工全过程的顶升力的预测方法。


技术实现要素：

9.本发明的目的是针对现有技术中存在的不足之处，提供一种垂直顶升法施工全过程的顶升力预测方法，能够更准确和动态地预估施工中需要的顶升力。为此，本发明采用以下技术方案
10.一种垂直顶升法施工全过程的顶升力预测方法，其特征在于包括以下步骤：
11.步骤一，确定垂直顶升法施工中顶升力的组成部分，
12.将垂直顶升法的顶升力f根据三部分匹配，分别为迎面阻力fy、管土间摩擦力ff和管自重g
p
；其中的迎面阻力fy是立管管盖处受力的总和；即有：f＝f
yb
+ff+g
p
；
13.步骤二，选择立管顶升过程中的受力模型，计算迎面阻力fy，
14.根据上覆土层的厚度将迎面阻力的受力分为两种受力模型，分别为球孔扩张-滑动摩擦模型和剪切破坏-滑动摩擦模型；当上覆土层较高，有f
yb
《f
ys
时，立管管盖处看成球孔扩张问题，则当上覆土层较低，有f
ys
《f
yb
时，立管管盖处土体破坏形式为剪切破坏，则fy＝f
ys
＝gs+gw+f
cf
，其中gs为剪切破坏线内土重(kn)，有
15.gs＝y
′
πa[r
d2
+r
m2
+rdrm]/3，gw为立管范围内水重(kn)，有f
cf
为剪切破线内因土体粘聚力引起的阻力(kn)，有f
yb
为球孔扩张-滑动摩擦模型下的迎面阻力(kn)，f
ys
为剪切破坏-滑动摩擦模型下的迎面阻力(kn)，pu为极限扩孔压力(kpa)，rd为立管半径(m)，γ'为土体有效重度(kn
·
m-3
)，h为立管管盖距泥面线高度(m)，rm为剪切破坏线延伸至泥面线与立管中心距离(m)，γw为水体重度(kn
·
m-3
)，h为水平隧道上侧距泥面线高度(m)，c为粘聚力(kpa)。
[0016]
步骤三，根据计算的f＝fy+ff+g
p
，计算顶升力。
[0017]
进一步地，管土间摩擦力ff的取值，按以下公式计算：ff＝μkπdl2[γ
′
h+γ
whw
+γw(h+h)/2]。μ为管土间摩擦系数，k为侧向土压力系数，d为立管外径(m)。
[0018]
进一步地，管自重g
p
的取值，按以下公式计算：g
p
＝ng
′
，n为已顶升管节数，g'为管节平均自重(kn)。
[0019]
本发明考虑了上覆土厚度的动态变化对迎面阻力的影响，具有更客观和全面的理论基础，能够更加准确的估算垂直顶升法施工全过程的顶升力。
附图说明
[0020]
图1为垂直顶升法施工时立管受力图。
[0021]
图2为球孔扩张-滑动摩擦立管受力示意图。
[0022]
图3为剪切破坏线-滑动摩擦立管受力示意图。
[0023]
图4为球孔扩张基本问题示意图。
[0024]
图5为顶升力求解流程图。
[0025]
图6为第一组立管顶升力结果对比图。
[0026]
图7为第二组立管顶升力结果对比图。
具体实施方式
[0027]
以下结合研究中的逻辑思辨过程，对本发明提供的一种垂直顶升法施工全过程的顶升力的计算方法进行详细说明。
[0028]
步骤一：确定垂直顶升法施工中顶升力的组成部分
[0029]
垂直顶升法在施工中，需要克服上部层层阻力，才能将立管顺利顶出，类似水平顶管施工工程中的受力分析，将垂直顶升法的顶升力对应三部分匹配(见图1)，立管主要受到：
①
迎面阻力fy；
②
管土间摩擦力ff；
③
管自重g
p
。其中的迎面阻力是立管管盖处受力的总和，也是本发明研究的重点内容。
[0030]
步骤二：建立立管顶升过程中的受力模型
[0031]
根据施工特点，迎面阻力的受力机理与上覆土层高度有关，当上覆土层较高时，垂直顶升过程可以看成是球孔扩张问题；当上覆土层较浅时，土体破坏形式为剪切破坏。基于
此，提出两种顶升力计算模型，当上覆土层高于阈值时，垂直顶升过程可以看成是球孔扩张问题，球孔扩张-滑动摩擦模型(见图2)；当上覆土层低于阈值时，土体破坏形式为剪切破坏，采用剪切破坏-滑动摩擦模型(见图3)；同时针对上述两种模型做以下假设：
[0032]
(1)球孔扩张-滑动摩擦模型假定初始半径为0，最终扩孔半径为立管半径；剪切破坏-滑动摩擦模型假定破坏线与竖直方向夹角为(2)当球孔扩张-滑动摩擦模型计算顶升力值小于剪切破坏-滑动摩擦模型顶升力值，垂直顶升发生球孔扩张屈服，否则只会发生剪切破坏；(3)初顶时，迎面阻力初始值取立管范围内水土压力，初顶至达到最大迎面阻力这段顶升过程中，迎面阻力随顶升距离呈线性变化，迎面阻力最大的位置发生在上覆土层的压缩量处；(4)立管与土之间接触为“全接触”，即管土之间接触充分。
[0033]
步骤三：建立顶升力各组成部分计算公式
[0034]
(一)球孔扩张-滑动摩擦模型迎面阻力f
yb
[0035]
球孔扩张基本问题如图4所示，平衡方程、几何方程、物理方程分别如下：
[0036]
dσr/dr+2(σ
r-σ
θ
)/r＝0
ꢀꢀꢀ(i)[0037][0038][0039]
式中：σr、σ
θ
分别为径向和切向应力，ur为径向位移，ν为泊松比，e为弹性模量；根据边界条件：
[0040][0041]
式中：r
p
为塑性区半径，ru为最终扩孔半径，在此处为d/2，σ
p
为临塑扩孔压力，p0为初始孔压，pu为极限扩孔压力；
[0042]
可以解出弹性区土体应力及位移解：
[0043][0044]
式中：g为剪切模量。
[0045]
土体屈服服从mohr-coulomb强度屈服准则，则有：
[0046][0047]
式中：c为粘聚力，为内摩擦角；
[0048]
结合边界条件，有：
[0049][0050]
在弹塑性应力边界处，土体会同时满足弹性区边界条件和塑性区边界条件，可得弹塑性分界处应力表达式为：
[0051][0052]
当r＝ru时，联立式(7)和式(8)，有：
[0053][0054]
式中：λ＝r
p
/ru。
[0055]
弹塑性分界处环向处应变ε
θp
、径向位移u
rp
可表示成为：
[0056][0057][0058]
对于塑性变形，carter
[3]
推导出塑性区径向位移可表达为：
[0059][0060]
t＝l-a+b
ꢀꢀꢀ
(13)
[0061][0062][0063][0064][0065][0066][0067][0068][0069]
式中：ψ为剪胀角，α、β、a、b、t、z、s、m、n均为无量纲中间参数。
[0070]
为了求解塑性区半径，引入塑性区体积应变δ：
[0071][0072]
结合式(2)和式(12)有：
[0073][0074]
其为塑性区体积变化与塑性区总体积的比值，扩孔前后，根据体积守恒有：
[0075]ru3-r
03
＝r
p3-(r
p-u
rp
)3+δ(r
p3-r
u3
)
ꢀꢀꢀ
(24)
[0076]
展开忽略u
rp
高阶项，并将式(11)代入有：
[0077][0078]
至此，即可求解出塑性区半径大小，具体求解过程如下：
[0079]
1)根据实验测得土体各参数，确定各类参数c、ψ、ν、e、g取值；
[0080]
2)根据土体参数，确定无量纲中间参数α、β、a、b、t、s；
[0081]
3)联立式(22)、(25)，通过matlab软件求解超越方程，求出λ，进而求解r
p
。
[0082]
则球孔扩张-滑动摩擦模型迎面阻力f
yb
取值有：
[0083][0084]
式中rd为立管半径。
[0085]
(二)剪切破坏-滑动摩擦模型迎面阻力f
ys
[0086]
根据图3，f
ys
可由下式计算：
[0087]fys
＝gs+gw+f
cf
ꢀꢀꢀ
(27)
[0088]gs
＝γ
′
πh[r
d2
+r
m2
+rdrm]/3
ꢀꢀꢀ
(28)
[0089][0090][0091][0092]
式中γ
′
为有效重度，γw为水的重度。
[0093]
(三)管土间摩擦力ff[0094]
管土之间摩擦力与顶升距离有关，一般可采用下式进行计算：
[0095][0096]
式中：μ为管土之间摩擦系数，k为侧向土压力系数，取值可取
[0097]
(四)管自重g
p
[0098]
立管自重与顶升管节有关，按下式计算：
[0099]gp
＝ng'
ꢀꢀꢀ
(33)
[0100]
式中：n为已顶升管节个数，g'为平均管节重量。
[0101]
步骤四：顶升力的选取
[0102]
至此，已经形成一套合理的预测顶升力的计算体系，只需知道立管所处位置、土层
参数以及立管尺寸等参数，即可计算顶升力大小，具体求解流程图见图5。
[0103]
当f
yb
《f
ys
时，有：
[0104]
f＝f
yb
+ff+g
p
ꢀꢀꢀ
(34)
[0105]
当f
ys
《f
yb
时，有：
[0106]
f＝f
ys
+ff+g
p
ꢀꢀꢀ
(35)
[0107]
以下结合具体实施例，进一步说明本发明技术方案的技术效果。
[0108]
选取某市取排水工程案例对垂直顶升法施工全过程的顶升力进行计算。该排水工程为污水处理厂尾水排海管工程，应用垂直顶升法施工的路段位于2号井和b3排污口之间，该区间总长1420m，水平隧道外径2m，壁厚22mm，距离排污口400m范围内顶升29根立管，立管直径为0.5m，壁厚20mm，每根立管顶升高度为12.5m，由1根长为0.5m的首节管节与20根长为0.6m的标准管节组成。本工程中海平面距泥面线高度为14.41m，泥面线距水平隧道上侧11.5m。
[0109]
根据立管穿破土质的条件可以将立管分为两组，第一组穿越单一土层，第二组穿越多层土层，选取第一组立管中顶升力最有代表性的3根立管和第二组立管中的2根立管合计5根立管作为典型进行顶升力的计算分析，第一组根立管分别发生在第3号、第4号和第5号立管，第二组立管发生在第11号、第12号立管，第一组立管需穿越11.5m的粗砾砂层以及1m的净水层。第二组立管穿越0.5m的粘土层、11m的粘土层以及1m的净水层。
[0110]
根据工程地质报告，粗粒砂土体重度19.8kn
·
m-3
，粘聚力为0，内摩擦角41.9
°
，压缩模量46mpa，粘土重度为19.6kn
·
m-3
，粘聚力为47.4kpa，内摩擦角13.2
°
，压缩模量12mpa。
[0111]
利用式(13)-(21)，计算塑性区半径r
p
，代入式(26)，并与式(27)比较，得到迎面阻力，利用式(32)、(33)计算，得到管土间摩阻力和管自重，根据式(34)、(35)，即可得到垂直顶升法施工过程中立管的顶升力计算值。为了更好地评价理论计算方法的正确性，将2组立管实测值与本文理论计算结果和目前主流计算方法结果进行对比，第一组立管顶升力结果对比图如图6所示，第二组立管顶升结果对比图如图7所示。此外，对于工程中最关心的最大顶升力，不同算法计算结果见表1。
[0112]
表1，不同算法最大顶升力对比表
[0113][0114]
本发明前文引用的文献如下：
[0115]
文献[1]王寿生,葛春辉.垂直顶管计算方法的探讨[j].特种结构,2009,26(5):18-21.
[0116]
文献[2]dg/tj 08-2049-2016顶管工程施工规程[s].同济大学出版社,2017.
[0117]
文献[3]carter j p,booker j r,yeung s k.cavity expansion in cohesive frictional soils[j].geotechnique,1986,36(3):349-358.
[0118]
文献[4]董胜宪,罗树青.垂直顶升法在电厂取排水隧道工程中的应用[j].电力勘
测设计,2012(6):47-51.
[0119]
文献[5]刘桂荣.大型核、火电厂取水结构施工技术研究[d].上海交通大学,2014.
[0120]
从图6可见：在顶升距离2.3m以前，f
yb
《f
ys
，采用式(34)计算，顶升距离2.9m及以后，f
ys
《f
yb
，采用式(35)计算。第一组立管最大顶升力分别为1920kn、2040kn、1760kn，平均值1906.7kn，本发明理论计算值1981.5kn，理论值偏大，相差3.9％，终止顶升力分别为760kn、510kn、510kn，平均值为593.3kn，本发明理论计算值为681.7kn，理论值偏大，相差14.9％。
[0121]
从图7可见：在顶升距离2.3m以前，f
yb
《f
ys
，采用式(34)计算，顶升距离2.9m及以后，f
ys
《f
yb
，采用式(35)计算。第二组立管最大顶升力均为2160kn，本发明理论计算值为1987.5kn，实测值偏大，相差8％，终止顶升力分别为510kn和640kn，平均值为575kn，本发明理论计算值为688.2kn，理论值偏大，相差19.7％。
[0122]
从图6、图7可以看出，实际工程中顶升力并非顶升首节管节时最大，而是呈现先增加后减小的两段式变化，对于最大顶升力出现的位置，第一组分别发生在2.9m、2.3m、2.9m，平均值为2.7m(0.235h)，第二组均发生在2.9m(0.252h)，本发明理论法计算值均为2.3m(0.2h)。
[0123]
此外，对于工程中最关心的最大顶升力，从表1可见：本发明计算法计算结果与实际值最接近，表明本发明推导的计算公式与该工程吻合较好。
[0124]
本工程实例表明，本发明基于球孔扩张法基本解和剪切破坏理论，考虑了上覆土厚度的动态变化对迎面阻力的影响，可为垂直顶升法施工全过程的顶升力计算方法提供理论参考。