一种基于超混沌系统与遗传粒子群算法的S盒设计方法

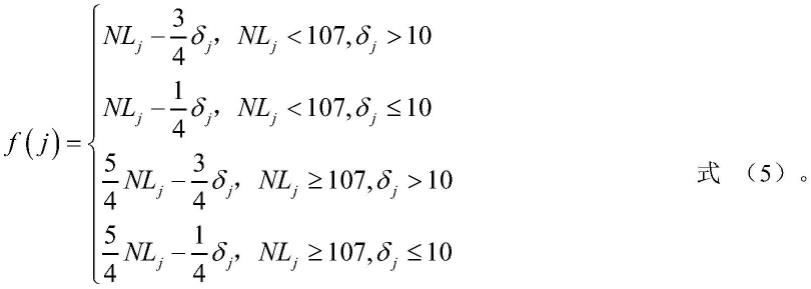
一种基于超混沌系统与遗传粒子群算法的s盒设计方法
技术领域
1.本发明涉及一种基于超混沌系统与遗传粒子群算法的s盒设计方法，属于混沌加密技术领域。


背景技术：

2.s盒是实现混乱和扩散的非线性部件，在分组密码aes、des中起混淆和替代的功能，同时也广泛应用于图像加密领域；起初，s盒的构造方式主要为代数方法，但这种方法难以同时兼顾s盒的多种密码特性，随后由于混沌理论的发展，将混沌系统的类随机性、非线性以及初值敏感性等密码特性用于构造安全的s盒的方法逐渐得到重视，目前提出了诸多使用 logistic映射、chebyshev映射、sine映射、tent映射等低维混沌系统的s盒构造方案，但是由于低维混沌系统的构造相对简单，迭代序列容易被预测，将其直接应用于加密领域中存在一定的风险，而高维混沌系统尤其是超混沌系统有更复杂的混沌行为，因而研究将结构更加复杂的超混沌映射应用于s盒设计成为关键。
3.此外，仅仅使用混沌系统构造s盒而缺乏相应的优化方案，会导致所构造的s盒性能过度依赖所使用的混沌系统，因而限制了s盒性能的提升。随着智能算法不断发展，基于混沌系统与智能算法的联合s盒构造方案受到越来越多的关注，出现了基于烟花算法、遗传算法、 jaya算法等优化算法的s盒构造方案。
4.在诸多使用优化算法对s盒进行优化的方案中，使用遗传算法进行s盒优化能产生最佳优化效果，遗传算法有着较强的全局搜索能力，通过交叉变异操作能够提高种群多样性，避免早熟现象；但是遗传算法也存在盲目搜索的问题，除此之外，由于遗传算法在进行交叉、变异操作时无法根据个体解的优劣程度动态改变交叉率与变异率，即采用固定的交叉率与变异率，因而使用遗传算法优化的s盒仍无法达到最佳优化效果。而粒子群优化算法能够保留粒子与种群的最优信息，通过对粒子与种群的信息共享进而影响群体的运动方向与速度，但粒子群算法也存在早熟收敛，易陷入局部误区的问题。基于两种算法各自的优缺点，将遗传算法与粒子群算法相结合可以有效提高优化效果。
5.目前，两种算法的混合方式主要为并行式混合、串行式混合以及嵌入式混合。并行式混合在优化的过程中，两种优化算法相互独立运行，算法间难以协作，导致各自的缺点依然存在；串行式混合优化时采用先后执行不同优化算法的方式，同样无法克服各自算法的缺点，且在优化算法进行相互切换时需要进行额外的处理，增加算法复杂度；嵌入式混合是将某一算法的思想加入到另一个算法中，基于遗传算法与粒子群优化算法的嵌入式混合方案主要是在粒子群算法进行迭代更新前或者更新后，加入遗传算法的选择、交叉、变异操作，以此提高种群的多样性，但也面临着如何合理设定交叉、变异率等参数的困难。


技术实现要素：

6.为了提高基于混沌系统所构造的s盒的非线性特征和差分均匀性从而增强抵抗线性攻击的能力，本发明提供了一种基于超混沌系统与遗传粒子群算法的s盒设计方法，所述
方法包括：
7.步骤1：构造基于chebyshev映射和icmic映射的二维混沌系统，并根据所述二维混沌系统构造若干初始s盒，计算每个初始s盒的非线性度以及差分均匀性；
8.步骤2：基于s盒性能评判原则确定遗传粒子群优化算法的适应度函数；
9.步骤3：对遗传粒子群优化算法中的粒子进行编码，每个粒子代表一个初始s盒；
10.步骤4：通过改进的遗传算法的交叉、变异操作进行粒子位置更新；所述改进的遗传算法中，使用粒子速度自适应地控制遗传算法的交叉率和变异率；
11.步骤5：判断更新后的粒子适应度值是否发生退化，若发生退化，返回步骤4，否则继续步骤6；
12.步骤6：更新局部最优解与全局最优解，判断是否达到最大迭代次数，若达到最大迭代次数，输出此时的全局最优解作为最终设计的s盒，否则，返回步骤4。
13.可选的，所述根据所述二维混沌系统构造若干初始s盒，包括：
14.根据下式(1)构造二维混沌系统；
[0015][0016]
式(1)中，x(n)、y(n)、x(n+1)和y(n+1)分别为第n+1次迭代的输入和输出值，其取值范围为[-1,1]；k为调制参数，取值范围为(0.2,1)；λ为系统参数，取值范围为λ≥2；
[0017]
对所构造的二维混沌系统赋初值x(0)、y(0)；设置系统参数k、λ；迭代l次，舍去前 1000个混沌序列，取剩余的混沌序列x(n)、y(n)；
[0018]
将[-1,1]区间等分为10000个小区间，按顺序给每个小区间标上序号i，i＝1,2,...,10000；接着取y(n)所在区间的区间号为y(n)，x(n)所在区间的区间号为x(n)；
[0019]
使用得到的y(n)，获取x(n)序列对应位置的值x(y(n))，将其依次填入空的数组h中，截取数组h中长度为256的片段来生成s盒；
[0020]
为了使得到的数值与8
×
8的s盒控制在同一范围内，通过公式(2)得到0到255范围内的整数s，将其填入s盒，如果得到的s值有重复，则需获得一个随机整数r1，随后使用公式(3)的s’替换该值：
[0021]
s＝mod(x(y(n)),256)
ꢀꢀꢀꢀꢀ
式(2)
[0022]
s'＝mod(y(n+r1),256)
ꢀꢀꢀꢀ
式(3)
[0023]
最后通过在数组h中截取不同的片段，获得不同的初始s盒。
[0024]
可选的，所述步骤2中遗传粒子群优化算法的适应度函数为：
[0025]
f(j)＝γ*nlj+θ*δjꢀꢀꢀꢀꢀꢀꢀꢀ
式(4)
[0026]
对于第j个粒子，即第j个s盒，nlj表示s盒的非线性度，δsj表示s盒的差分均匀度，γ，θ为加权系数；所述s盒性能评判原则为非线性越大、差分均匀性越小的s盒性能越好；
[0027]
基于s盒性能评判原则，对γ，θ进行分段赋值，得到的适应度函数如下所示：
[0028][0029]
可选的，所述步骤3包括：
[0030]
使用十进制整数编码方式对粒子进行编码，将步骤1所得到的各初始s盒表示为一个由0
‑ꢀ
255所有整数构成的无重复的全排列；
[0031]
设定种群数量为n，粒子的空间维数d为256，则第j个粒子表示为[p1,p2,
…
,pd]。
[0032]
可选的，所述步骤4中交叉率指交叉片段长度，所述变异率指变异次数。
[0033]
可选的，所述步骤4包括：
[0034]
利用下式(5)进行粒子速度更新：
[0035][0036]
其中，第j个粒子的d个元素与局部最优解的d个元素按位置进行比较，记录其中相同位置上元素不同的个数及序号，不同元素的个数就是该粒子与局部最优解的距离d1，粒子与全局最优解的距离为d2；
[0037]
r2和r3为两个取值范围为(0,1)的随机数，iter表示当前迭代次数，ger表示最大迭代次数； c1为自我学习因子，c2为群体学习因子，w为惯性权重，v(j-1)为上一轮迭代的速度，v(j) 表示本轮粒子速度；
[0038]
对获得的粒子速度v(j)向上取整，得到的值作为第j个交叉片段的长度l1(j)；
[0039]
将上一轮得到的n个局部最优解按照适应度值由大到小进行排序，取前30％，从中随机选取一个作为交叉操作的亲代p1，将第j个粒子作为亲代p2；
[0040]
接着选取一个取值范围为(1,256)的随机整数r4作为交叉的起始位置，选取的随机数需要满足r4+l1(j)≤256，然后交换两个亲代中从r4到r4+l1(j)的位置；
[0041]
最后做冲突检测，根据交换的片段中的对应元素建立一个映射关系，所有冲突的元素都会经过映射进行替换，保证形成的子代中不会有重复的元素；
[0042]
利用下式(6)得到l2(j)，向上取整获得变异次数l2(j)：
[0043][0044]
其中，f(j)为第j个粒子的适应度值，f
p
(j)为局部最优解相应的适应度值，fg为全局最优解相应的适应度值；随机选取两个取值范围为(1,256)且不相等的整数并交换这两个位置上的元素，重复该操作l2(j)次即得到位置更新后的粒子。
[0045]
可选的，所述步骤5包括：
[0046]
计算交叉变异操作后的粒子适应度值，若得到的粒子适应度值小于交叉变异操作前的粒子适应度值，表明粒子发生退化，则返回步骤4再次进行交叉变异操作。
[0047]
可选的，所述步骤6包括：
[0048]
通过适应度函数计算各个粒子的适应度值f(j)，得到n个局部最优解，相应的适应度值为f
p
(j)；从局部最优解中找出适应度值最高的粒子作为全局最优解，其适应度值为fg。所述适应度值最高的粒子所代表的初始s盒即为最终设计的s盒。
[0049]
可选的，所述步骤1中构造基于chebyshev映射和icmic映射的二维混沌系统，包括：
[0050]
级联调制耦合模型cmc表达式如下所示：
[0051][0052]
其中f和g为两种一维混沌映射，f为一个线性方程，表达式为f(t)＝t+3；
[0053]
在级联调制耦合模型cmc基础上，使用带平方项的非线性方程代替原本的线性部分，得到级联调制耦合模型，表达式如下所示：
[0054][0055]
其中，x(n)、y(n)是状态量，k是调制参数，f和g两种一维混沌映射。
[0056]
基于所述级联调制耦合模型，f和g分别采用chebyshev映射和icmic映射，根据式 (1)构造二维混沌系统，其数学表达式如下：
[0057][0058]
本技术还提供一种数据及图像加密方法，所述方法采用上述方法设计的s盒进行混淆和替代操作以实现对于数据及图像的加密。
[0059]
本发明有益效果是：
[0060]
通过提出一个基于chebyshev映射和icmic映射的二维级联调制耦合混沌系统，分析表明该混沌系统在参数范围内是超混沌的，所生成的混沌序列具有更好的遍历性，且其混沌行为更加难以预测。在改混沌系统的基础之上，采用区间划分法和序列索引的方法生成性能良好的s盒，最后使用遗传粒子群优化算法对s盒进行的优化可获得了非线性度更高的s 盒。与现有方案相比，本技术所构造的s盒在非线性度、差分均匀性、输出比特间独立性方面均具有良好表现，抵抗线性攻击的能力更强，在数据及图像加密领域有着广泛的应用前景。
具体实施方式
[0061]
为使本发明的目的、技术方案和优点更加清楚，下面将对本发明实施方式作进一步地详细描述。
[0062]
实施例一：
[0063]
本实施例提供一种基于超混沌系统与遗传粒子群算法的s盒设计方法，所述方法包括：
[0064]
步骤1：根据改进的二维混沌系统生成的混沌序列构造初始s盒；
[0065]
所述改进的二维混沌系统改进过程如下：
[0066]
设计级联调制耦合模型cmc，其表达式如下所示：
[0067][0068]
其中f和g为两种一维混沌映射，f为一个线性方程，表达式为f(t)＝t+3；
[0069]
在级联调制耦合模型cmc基础上，使用带平方项的非线性方程代替原本的线性部分，由于y(n)和x(n+1)取值范围都在-1到1之间，因而使用平方项可以扩大y(n)和x(n+1)的取值差异性，进而增加对输入的扰动力度；除此之外，对两个输出表达式使用不同的非线性方程，能够进一步提升整个模型的复杂度，使输出的混沌序列有着良好的不可预测性。
[0070]
得到级联调制耦合模型，表达式如下所示：
[0071][0072]
其中，x(n)、y(n)是状态量，k是调制参数，f和g两种一维混沌映射。
[0073]
基于所述级联调制耦合模型，f和g分别采用chebyshev映射和icmic映射，采用下式(1)构造二维混沌系统；
[0074][0075]
式(1)中，x(n)、y(n)、x(n+1)和y(n+1)分别为第n次迭代的输入和输出值，其取值范围为[-1,1]；k为调制参数，取值范围为(0.2,1)；λ为系统参数，取值范围为λ≥2。
[0076]
对混沌系统赋初值x(0)、y(0)；设置系统参数k、λ。迭代l次，舍去前1000个混沌序列，取剩余的混沌序列x(n)、y(n)。
[0077]
将[-1,1]区间等分为10000个小区间，按顺序给每个小区间标上序号i，i＝1,2,...,10000。接着取y(n)所在区间的区间号为y(n)，x(n)所在区间的区间号为x(n)。
[0078]
使用得到的y(n)，获取x(n)序列对应位置的值x(y(n))，将其依次填入空的数组h中，截取数组h中长度为256的片段来生成s盒。
[0079]
为了使得到的数值与8
×
8的s盒控制在同一范围内，通过公式(2)得到0到255范围内的整数s，将其填入s盒，如果得到的s值有重复，则需获得一个随机整数r1，随后使用公式
(3)的s’替换该值。
[0080]
s＝mod(x(y(n)),256)
ꢀꢀꢀꢀꢀꢀ
式(2)
[0081]
s'＝mod(y(n+r1),256)
ꢀꢀꢀꢀꢀꢀ
式(3)
[0082]
通过在数组h中截取不同的片段，即可获得不同的初始s盒，计算每个初始s盒的非线性度以及差分均匀性。
[0083]
步骤2：根据初始s盒的非线性度以及差分均匀性设置遗传粒子群优化算法的适应度函数；
[0084]
利用下式(4)得到遗传粒子群优化算法的适应度函数：
[0085]
f(j)＝γ*nlj+θ*δjꢀꢀꢀꢀꢀꢀꢀꢀ
式(4)
[0086]
对于第j个粒子，即第j个s盒，nlj表示s盒的非线性度，δsj表示s盒的差分均匀度，γ，θ为加权系数，非线性越大、差分均匀性越小的s盒性能越好，基于这个原则，对γ，θ进行分段赋值，经测试得到的适应度函数如下所示：
[0087][0088]
步骤3：对遗传粒子群优化算法中的粒子进行编码；
[0089]
使用十进制整数编码方式对粒子，即s盒进行编码，将双射s盒看做一个由0-255所有整数构成的无重复的全排列。设定种群数量为n，空间维数为d，则第j个粒子为 [p1,p2,
…
,pd]。
[0090]
步骤4：通过改进的遗传算法交叉、变异操作进行粒子位置更新；
[0091]
利用下式(5)进行粒子速度更新：
[0092][0093]
其中，第j个粒子的256个元素与局部最优解的256个元素进行比较，记录其中相同位置上元素不同的个数及序号，不同元素的个数就是该粒子与局部最优解的距离d1，粒子与全局最优解的距离d2，r2和r3为两个取值范围为(0,1)的随机数，iter表示当前迭代次数，ger 表示最大迭代次数；c1为自我学习因子，c2为群体学习因子，w为惯性权重，v(j-1)为上一轮迭代的速度，v(j)为本轮粒子速度。
[0094]
对获得的粒子速度v(j)向上取整，得到的值作为第j个交叉片段的长度l1(j)；
[0095]
将上一轮得到的n个局部最优解按照适应度值由大到小进行排序，取前30％，从中随机选取一个作为交叉操作的亲代p1，将第j个粒子作为亲代p2。
[0096]
接着选取一个取值范围为(1,256)的随机整数r4作为交叉的起始位置，选取的随机数需要满足r4+l1(j)≤256，然后交换两个亲代中从r4到r4+l1(j)的位置；最后做冲突检
测，根据交换的片段中的对应元素建立一个映射关系，所有冲突的元素都会经过映射进行替换，保证形成的子代中不会有重复的元素。
[0097]
利用下式(6)得到l2(j)，向上取整获得变异次数l2(j)：
[0098][0099]
其中，f(j)为各个粒子的适应度值，f
p
(j)为局部最优解相应的适应度值，fg为全局最优解相应的适应度值。随机选取两个取值范围为(1,256)且不相等的整数并交换这两个位置上的元素，重复该操作l2(j)次。
[0100]
步骤5：判断更新后的粒子适应度值是否发生退化，若发生退化，返回步骤4，否则继续步骤6；
[0101]
计算交叉变异操作后的粒子适应度值，若得到的粒子适应度值小于交叉变异操作前的粒子适应度值，则表明粒子发生退化，因此返回步骤4再次进行交叉变异操作。
[0102]
步骤6：更新局部最优解与全局最优解，判断是否达到最大迭代次数，若达到最大迭代次数，输出此时的全局最优解作为最终结果，否则，返回步骤4。
[0103]
通过适应度函数计算各个粒子的适应度值f(j)，得到n个局部最优解，相应的适应度值为f
p
(j)；从局部最优解中找出适应度值最高的粒子作为全局最优解，其适应度值为fg。
[0104]
为使本发明的目的、技术方案和优点更加清楚，下面将利用一些目前提出的s盒构造方法与所提出的方法作对比，展现基于超混沌系统与遗传粒子群算法的s盒设计方法性能方面的优越性。
[0105]
用来对比的方案分别是：
[0106]
方案一(基于sine混沌映射构造s盒)，可参考belaziakram,ahmeda.abdel-latif.asimpleyetefficients-boxmethodbasedonchaoticsinemap[j].optik,2017,130:1438-1444.；
[0107]
方案二(基于tent
–
logistic复合混沌系统构造s盒)，可参考luq,zhuc,wangg.anovels-boxdesignalgorithmbasedonanewcompoundchaoticsystem[j].entropy,2019,21(10):1004；
[0108]
方案三(首先使用tent混沌映射获得伪随机序列并划分区间存储，随后使用该伪随机序列作为henon映射的初值，使用henon映射得到的256个非重复值构造s盒)，可参考韩妍妍,何彦茹,刘培鹤,等.一种基于混沌系统的zuc动态s盒构造及应用方案[j].计算机研究与发展,2020,57(10):11；
[0109]
方案四(首先使用lorenz三维混沌系统生成初始解，随后使用烟花算法对混沌系统解空间进行搜索，得到最优解后整数化并进行对应行列互换构造s盒)，可参考wangj,panb,tangc,etal.constructionmethodandperformanceanalysisofchaotics-boxbasedonfireworksalgorithm[j].internationaljournalofbifurcationandchaos,2019,29(12):1950158；
[0110]
方案五(首先使用logistic混沌映射构造初始s盒，随后使用遗传算法对初始s盒进行非线性度优化，得到非线性度良好的s盒)，可参考guesmir,farahmab,kachouri
a,etal.anoveldesignofchaosbaseds-boxesusinggeneticalgorithmtechniques[c]//2014ieee/acs11thinternationalconferenceoncomputersystemsandapplications(aiccsa).ieee,2014:678-684；
[0111]
方案六(首先使用所提出的混沌系统得到初始s盒，随后使用混沌jaya算法对初始s盒进行非线性度优化，得到非线性度良好的s盒)，可参考farahma,faraha,faraht.animageencryptionschemebasedonanewhybridchaoticmapandoptimizedsubstitutionbox[j].nonlineardynamics,2020,99(4):3041-3064；
[0112]
实验结果如表1、2、3、4所示；根据实验结果可知，本技术提出的基于超混沌系统与遗传粒子群算法的s盒设计方法展现出良好的非线性度、差分均匀性以及严格雪崩准则的位独立性。
[0113]
表1是本发明在x(0)＝0.5，y(0)＝0.5，k＝0.7，λ＝8，l＝11000，n＝30，d＝256，ger＝50，c1＝0.5，c2＝0.5，w＝0.8，vlimit＝[10,65]时生成的s盒在非线性度的比较结果，如下所示：
[0114]
表1：各方案与本技术所设计的s盒的非线性度的比较结果
[0115][0116][0117]
非线性度通常用来衡量s盒抵抗线性攻击的能力，非线性度的大小决定着一个密码系统的安全性。s盒中如果存在线性结构或是类似线性的结构，攻击者可以利用线性结构进行攻击，以此来获取密钥，甚至破译整个密码系统。使用walsh谱进行布尔函数非线性度计算结果如表1所示，所设计的s盒非线性度越大，其抵抗线性攻击的能力越高，安全性也就越高。经计算，本技术混沌系统构造的初始s盒的计算结果为106.50；经本技术方案优化后的s盒计算结果为108.25。与其他方案进行比较，基于本发明所构造的s盒的非线性度大于其他文献，其抵抗线性攻击方面的能力更强。
[0118]
表2是本发明在x(0)＝0.5，y(0)＝0.5，k＝0.7，λ＝8，l＝11000，n＝30，d＝256，ger＝50，c1＝0.5，c2＝0.5，w＝0.8，vlimit＝[10,65]时生成的s盒相关矩阵元素平均值的比较结果，如下所示：
[0119]
表2：各方案与本技术所设计的s盒的相关矩阵元素平均值的比较结果
[0120][0121]
s盒相关矩阵元素平均值通常用于衡量s盒是否遵循严格雪崩准则。严格雪崩准则 (strict avalanche criterion，sac)可以用来评判序列输入与输出变化的相关性。严格雪崩准则可以通过计算相关矩阵的方法进行检验，将矩阵中的元素看作是当s盒的输入比特改变时，输出比特改变的概率。通常，如果输入改变1比特时，每个输出比特改变的概率接近50％则表示该s盒满足严格雪崩准则。经计算，基于本发明所构造的s盒相关矩阵平均值为0.5031，接近0.5，因而满足严格雪崩准则。
[0122]
表3是本发明在x(0)＝0.5，y(0)＝0.5，k＝0.7，λ＝8，l＝11000，n＝30，d＝256，ger＝50， c1＝0.5，c2＝0.5，w＝0.8，vlimit＝[10,65]时生成的s盒最大差分值的比较结果，如下所示：
[0123]
表3：各方案与本技术所设计的s盒的最大差分值的比较结果
[0124][0125][0126]
差分密码分析是进行密码攻击的方式之一，而差分均匀性是针对差分密码分析引入的， s盒的差分均匀性是衡量其抵抗差分密码分析能力的重要指标，一个s盒的最大差分值越小，则表明其差分均匀性越好。从表中看出本技术中所设计的s盒最大差分值为10，优于或等于其他方案。
[0127]
表4是本发明在x(0)＝0.5，y(0)＝0.5，k＝0.7，λ＝8，l＝11000，n＝30，d＝256，ger＝50， c1＝0.5，c2＝0.5，w＝0.8，vlimit＝[10,65]时生成的s盒严格雪崩准则的位独立性的比较结果，如下所示：
[0128]
表4：各方案与本技术所设计的s盒的严格雪崩准则的位独立性的比较结果
[0129][0130]
上述表4为s盒严格雪崩准则的位独立性的比较结果，根据输出比特间独立性准则，输出值对输入值的位变化响应是独立的，即当输入的第t位发生改变时，输出的第m位和第n 位会独立地产生变化。本技术中采用严格雪崩准则的位独立性准则(bic-sac)来验证所构造的s盒的输出比特间独立性。bic-sac用于判断s盒的输出比特sm⊕
sj(sm和sn分别表示第m个和第n个布尔函数分量，且m≠n)是否满足严格雪崩准则。结果表明本技术最终生成的s盒严格雪崩准则平均值与理论值0.5仅相差0.0003，低于其他方案，表示所设计的s 盒有着较强的输出比特间独立性。
[0131]
综上可知，本技术方法所设计的s盒的非线性度、差分均匀性、输出比特间独立性方面均具有良好表现，其抵抗线性攻击的能力更强，基于该s盒进行数据及图像加密具有更高的安全性。
[0132]
本发明实施例中的部分步骤，可以利用软件实现，相应的软件程序可以存储在可读取的存储介质中，如光盘或硬盘等。
[0133]
以上所述仅为本发明的较佳实施例，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。