一种水轮机启停工况流场仿真预测方法及系统与流程

1.本发明涉及一种水轮机启停工况流场仿真预测方法及系统，属于水力机械技术领域。


背景技术：

2.水电站凭借着启停迅速的优点，在电力系统中还发挥着系统调峰、调频、调相及事故备用的作用。
3.中国专利（公布号cn103853884a）公开了一种水轮机活动导叶振动特性预测方法，其利用设计工况流量作为流体计算的进口边界条件，求得导叶初始设计构型下的稳态流场作为流场初值条件；在一个时间步内交替调用结构计算模块和流体计算模块，满足收敛条件后，流体和结构计算整体同步向前推进；通过界面信息交换模块传递流固边界信息；输出时间历程上的结构振动位移。上述发明实现导叶与流场的耦合计算，本发明准确性较以往单纯的结构动力学方法和单向耦合方法有了显著的提高，而且能够观察整个导叶振动发展过程，有利于更好地指导结构设计，使流固耦合从理论研究走上实际工程应用。
4.然而水轮机启停的过程中，水轮机会经历从空载到满载的过程。由于处在非设计工况，尾水管进口处的水流具有较大的切向速度，使水流产生涡带，这会导致尾水管产生强烈的压力脉动现象。
5.这种突变的运行工况，由于负载的变化，会导致振动频发，这对整个机组的稳定性乃至电站安全都会有较大的影响。同时，这种振动对设备的冲击较大，特别是会对过流部件造成疲劳损伤，缩短设备运行寿命。因此，科学、准确地预测水轮机在启停工况下的流场状态对整个水电站的运维具有较大的指导意义。
6.但上述发明方案没有公开如何科学、合理地预测启停工况下的流场状态以及压力脉动信息，从而影响水轮机的安全运行。
7.同时，由于水轮机内部流场复杂，且无法安装监测系统来获得流体流动情况，想要获得准确的速度和压力脉动信息存在较大难度。为了配合电网调度，电站水轮机会频繁地经历启停工况，如果不能科学地预测启停工况下的压力脉动信息，将无法保证水轮机的安全运行。
8.进一步，随着计算流体力学（cfd）的不断发展，数值模拟的计算速度和结果准确性的大大提升，研究人员提出了通过数值仿真的方式来模拟水轮机内流场流动情况，获得尾水管压力脉动信息。
9.目前，针对各类水轮机各种定工况下的数值模拟研究已获得了不错的成果，但针对启停这一特殊工况下的研究目前尚未得到充分的研究。
10.网格作为cfd计算的输入文件，不仅包含了模拟区域的几何信息，网格质量也直接影响计算的速度和精度。水轮机通过改变导叶开度来调节工况，一次启动，活动导叶都经历从全闭到全开的过程，这就会造成水轮机流体域几何结构的变化，而且这个变化是基本覆盖水轮机整个启动过程。基于以上原因，加上水轮机内流场本身复杂程度较高，这就导致了
启停工况数值模拟工作难以展开。


技术实现要素：

11.针对现有技术的缺陷，本发明的目的一在于提供一种构建网格模型以及动网格模型，从而可以根据水轮机启停工况下活动导叶运动过程，确定网格运动方式，在计算过程中，流体域网格几何形状可以自动变化，以匹配真实的物理状况，实现流体动、静状态的准确描述；同时利用计算流体力学cfd模型，得到水轮机启停工况下状态变化，实现水轮机启停工况下内流场状态和压力脉动情况的仿真以及预测，进而可指导水电站运维的水轮机启停工况流场仿真预测方法。
12.本发明的目的二在于提供一种设置几何模块、网格模块、动网格模块对启停工况下，导叶开度变化导致的流体域几何模型变化进行准确描述，进而能够实现启停工况下的数值模拟仿真，有效提升水轮机的数值模拟精度；并利用流体力学计算模块、水电站运维模块，得到水轮机启停工况下状态变化，实现水轮机启停工况下内流场状态和压力脉动情况的仿真以及预测，进而可指导水电站运维，方案科学、合理，切实可行，利于推广，便于实施的水轮机启停工况流场预测系统。
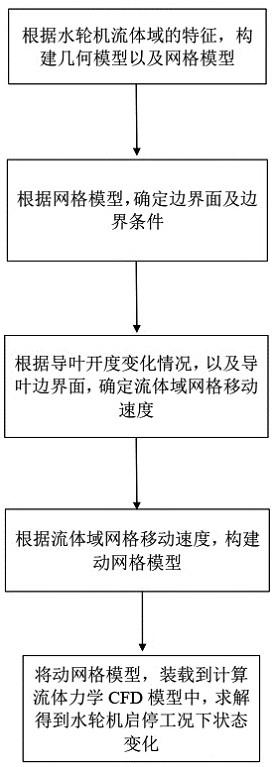
13.为实现上述目的之一，本发明的第一技术方案为：一种水轮机启停工况流场仿真预测方法，包括如下步骤：步骤1，根据水轮机流体域的特征，构建几何模型；步骤2，对步骤1中的几何模型进行分块，生成网格模型，用以描述流体域静止状态下的几何形状；步骤3，根据步骤2中的网格模型，确定边界面及边界条件；步骤4，根据水轮机启停工况过程中，导叶开度变化情况，以及步骤3中的导叶边界面，确定流体域网格移动速度；步骤5，根据步骤4中的流体域网格移动速度，构建动网格模型，用以生成变化的流体域网格，描述变化的几何形状，以匹配水轮机在实际启停工况下的物理状况；步骤6，将步骤5中的动网格模型，装载到计算流体力学cfd模型中，求解得到水轮机启停工况下状态变化，实现水轮机启停工况流场的仿真；所述状态变化包括内流场的状态变化、压力脉动状态信息；步骤7，根据步骤6中的内流场的状态变化、压力脉动状态信息，预测水轮机启停工况下内流场状态和压力脉动情况，辅助水电站运维。
14.本发明经过不断探索以及试验，构建网格模型以及动网格模型，从而可以根据水轮机启停工况下活动导叶运动过程，确定网格运动方式，在计算过程中，流体域网格几何形状可以自动变化，以匹配真实的物理状况。同时利用计算流体力学cfd模型，得到水轮机启停工况下状态变化，实现水轮机启停工况下内流场状态和压力脉动情况的仿真以及预测，进而可指导水电站运维。
15.本发明充分考虑预测水轮机启停工况流场状态的需求，以及数值模拟存在的几个难题，设置网格模型，用于描述静止状态的流体域网格几何形状；并设置动网格模型对启停工况下，导叶开度变化导致的流体域几何模型变化进行准确描述，进而根据流体动、静状态
的准确描述，能够实现启停工况下的数值模拟仿真，有效提升水轮机的数值模拟精度，能够有效确保水轮机的安全运行，方案科学、合理，切实可行，利于推广，便于实施。
16.作为优选技术措施：所述步骤1中，几何模型利用水轮机流体域全流道的cad模型进行构建。
17.作为优选技术措施：所述步骤2中，所述网格模型根据湍流模型进行构建，并设置壁面网格厚度。
18.作为优选技术措施：所述步骤4中，流体域网格移动速度的确定方法如下：步骤41，获取每片导叶旋转轴的旋转轴坐标，确定每片导叶旋转中心；步骤42，遍历边界面上的网格单元的坐标信息，获取每个边界面上的中心坐标，并使用绕轴旋转公式，确定叶片绕轴旋转的方向；步骤43，根据步骤41中的旋转中心以及步骤42中的中心坐标，得到边界面相对于旋转中心的坐标；步骤44，根据步骤43中的边界面相对于旋转中心的坐标，得到边界面距旋转中心的距离和相对于坐标轴的夹角；步骤45，根据步骤44中的边界面距旋转中心的距离和相对于坐标轴的夹角，以及启停工况下的导叶转动速率变化，计算导叶随时间变化的转速；步骤46，根据步骤45中的转速，计算每个边界面的网格运动速度。
19.作为优选技术措施：边界面相对于旋转中心坐标的计算公式如下：；其中，,为边界面相对于旋转中心的坐标；x0, y0为导叶旋转中心的坐标；xn, yn为边界面的中心坐标；边界面距旋转中心距离的计算公式如下：边界面相对于坐标轴夹角的计算公式如下：边界面网格运动速度的计算公式如下：其中， w为导叶转动速度；
为边界面网格在x轴上的运动速度；为边界面网格在y轴上的运动速度。
20.作为优选技术措施：所述步骤5中，动网格模型通过使用任意拉格朗日-欧拉方法，求解网格运动的控制方程组，得到全局网格节点的运动信息，其生成方法如下：步骤51，获取网格运动的速度场，其计算公式如下：其中，v(x, t)表示网格运动的速度场；x(x0, t)表示初始位于x0的点在t时刻的坐标；步骤52，根据步骤51中的速度场，通过莱布尼茨积分定则，计算上一时刻网格的某单元内张量场v在ωc(t)中随时间的变化，其计算公式如下：其中，ω(t)为随时间变化的流体域，ds为面微元；ωc(t)为流体域ω(t)的子域，其对应于上一时刻网格的一个单元；d/dt表示积分量的总导数，积分随ωc(t)变化而变化；步骤53，根据步骤52中的张量场v，并利用莱布尼茨积分定则，得到网格单元的体积运动方程，其计算公式如下：同时，分别对密度场ρ和动量场使用莱布尼茨积分定则，得到网格质量方程、动量守恒方程：其中，为流体速度，为应力场，为网格单元的体积微元；步骤54，对步骤53中的体积运动方程、网格质量方程、动量守恒方程作一个时间步上的积分，得到网格运动时间相关的控制方程组：
其中，所有的n上标表示第n时间步时的物理量，、、分别表示第n时间步时，该网格单元的体积、质量和动量；tn为第n时间步；为ωc的所有面单元，f表示中的一个面，、、分别表示面f的面积、速度和应力张量。
21.步骤55，根据控制方程组，得到网格移动的全场解，根据全场解改变流体域网格几何形状，以匹配水轮机在实际启停工况下的物理状况。
22.在确定网格运动时，只需要确定边界面处的网格移动，通过使用任意拉格朗日-欧拉方法，求解网格运动守恒方程，得到全局网格节点的运动信息，方案简单实用，切实可行。
23.作为优选技术措施：所述网格运动的速度场通过求解流体域ω(t)上的泊松方程得到，所述泊松方程的计算公式如下：的计算公式如下：其中：
∂
ω
imp
(t)表示具有网格移动速度或位移的边界；
∂
ω\
∂
ω
imp
(t)是固定边界；为面的法向向量；imposed velocity为定义的网格运动速度；λ为单位矩阵。
24.水轮机启停工况下，由活动导叶开度变化造成流体域几何结构变化，在此动网格模型的基础上，只需得到活动导叶边界面上网格移动的速度，就能得到网格移动的全场解，实现网格变化的定量计算，方案切实可行。
25.作为优选技术措施：所述步骤6中，计算流体力学cfd模型根据流体力学控制方程进行构建，其具体的构建方法如下：步骤61，构建质量守恒方程和动量守恒方程，其计算公式分别如下所示：其中，为流体速度，ρ为流体密度即密度场，为应力场，为体积力源项；步骤62，对步骤61中的质量守恒方程和动量守恒方程分别进行时间和空间上的离散，其具体包括以下内容：所述质量守恒方程进行时间上离散的方程如下：其中δt为时间步的步长；所述动量守恒方程进行时间上离散的方程如下：对质量守恒方程和动量守恒方程，利用有限体积方法，进行空间上的离散；步骤63，步骤62中的离散完成后，使用显式压力场进行速度预测，再进行一个校正计算，并利用连续性方程用于计算压力的变化；所述校正的方法为通过调整质量通量以确保质量守恒，然后更新速度场。
26.作为优选技术措施：所述单元体积的计算公式如下： 所述单元质量的计算公式如下： 所述单元动量的计算公式如下：
其中，为单元体积，为单元质量，为单元动量，为网格单元的体积微元；对δt，第n步到第n+1步，一个时间步的积分的计算公式如下：（.）n表示第n时间步的物理量。
27.为实现上述目的之一，本发明的第二技术方案为：一种水轮机启停工况流场预测系统，应用上述的一种水轮机启停工况流场仿真预测方法；其包括几何模块、网格模块、动网格模块、流体力学计算模块、水电站运维模块；所述几何模块，用于描述水轮机流体域的几何特征；所述网格模块，用于描述初始状态的流体域网格几何形状；所述动网格模块，用于描述变化状态的流体域网格几何形状；所述流体力学计算模块，用于计算水轮机启停工况下内流场的状态变化、压力脉动状态信息；所述水电站运维模块，用于指导水电站运维。
28.本发明充分考虑预测水轮机启停工况流场状态的需求，以及数值模拟存在的几个难题，设置几何模块、网格模块、动网格模块对启停工况下，导叶开度变化导致的流体域几何模型变化进行准确描述，进而能够实现启停工况下的数值模拟仿真，有效提升水轮机的数值模拟精度；并利用流体力学计算模块、水电站运维模块，得到水轮机启停工况下状态变化，实现水轮机启停工况下内流场状态和压力脉动情况的仿真以及预测，进而可指导水电站运维，方案科学、合理，切实可行，利于推广，便于实施。
29.与现有技术相比，本发明具有以下有益效果：本发明经过不断探索以及试验，构建网格模型以及动网格模型，从而可以根据水轮机启停工况下活动导叶运动过程，确定网格运动方式，在计算过程中，流体域网格几何形状可以自动变化，以匹配真实的物理状况。同时利用计算流体力学cfd模型，得到水轮机启停工况下状态变化，实现水轮机启停工况下内流场状态和压力脉动情况的仿真以及预测，进而可指导水电站运维。
30.进一步，本发明充分考虑预测水轮机启停工况流场状态的需求，以及数值模拟存在的几个难题，设置几何模块、网格模块、动网格模块对启停工况下，导叶开度变化导致的流体域几何模型变化进行准确描述，进而根据流体动、静状态的准确描述，能够实现启停工况下的数值模拟仿真，有效提升水轮机的数值模拟精度；并利用流体力学计算模块、水电站运维模块，得到水轮机启停工况下状态变化，实现水轮机启停工况下内流场状态和压力脉动情况的仿真以及预测，进而可指导水电站运维，方案科学、合理，切实可行，利于推广，便
于实施。
附图说明
31.图1为本发明水轮机启停工况下预测方法流程图；图2为本发明导叶旋转导致开度变化状态图；图3为本发明仿真实施例水轮机结构图。
具体实施方式
32.为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。
33.相反，本发明涵盖任何由权利要求定义的在本发明的精髓和范围上做的替代、修改、等效方法以及方案。进一步，为了使公众对本发明有更好的了解，在下文对本发明的细节描述中，详尽描述了一些特定的细节部分。对本领域技术人员来说没有这些细节部分的描述也可以完全理解本发明。
34.如图1所示，本发明水轮机启停工况流场仿真预测方法的一种具体实施例：一种水轮机启停工况流场仿真预测方法，包括如下步骤：步骤1，根据水轮机流体域的特征，构建几何模型；步骤2，对步骤1中的几何模型进行分块，生成网格模型，用以描述流体域静止状态下的几何形状；步骤3，根据步骤2中的网格模型，确定边界面及边界条件；步骤4，根据水轮机启停工况过程中，导叶开度变化情况，可参见图2，以及步骤3中的导叶边界面，确定流体域网格移动速度；步骤5，根据步骤4中的流体域网格移动速度，构建动网格模型，用以生成变化的流体域网格，描述变化的几何形状，以匹配水轮机在实际启停工况下的物理状况；步骤6，将步骤5中的动网格模型，装载到计算流体力学cfd模型中，求解得到水轮机启停工况下状态变化，实现水轮机启停工况流场的仿真；所述状态变化包括内流场的状态变化、压力脉动状态信息；步骤7，根据步骤6中的内流场的状态变化、压力脉动状态信息，预测水轮机启停工况下内流场状态和压力脉动情况，辅助水电站运维。
35.本发明水轮机启停工况流场仿真预测方法的一种最佳具体实施例：一种水轮机启停工况流场仿真预测方法，包括以下内容：首先，给出在随时间变化的流体域ω(t)内的守恒控制方程。用v(x, t)表示网格运动的速度场。其中，点x(x0, t)表示初始位于x0的点在t时刻的坐标。因此网格运动的速度场的计算公式如下：
现在考虑ω(t)的子域ωc(t)，该域对应于上一时刻网格的一个单元。
36.使用莱布尼茨积分定则（或reynolds输运定理），可以得到任意张量场v在ωc(t)中随时间的变化（这里v为一阶张量，即向量，莱布尼茨积分定则适用于任意阶数的张量），其具体的计算公式如下：这里d/dt表示积分量的总导数，积分随ωc(t)变化而变化。
37.对单位标量场使用莱布尼茨积分定则，得到网格单元体积运动的形式。
38.同理，分别对密度场ρ和动量场使用莱布尼茨积分定则，得到网格质量、动量守恒方程：对体积、质量、动量三个方程作一个时间步上的积分，得到网格运动时间相关的守恒方程：这样就得到了网格运动的控制方程组，任意的网格运动速度场v(x, t)均需满足这三个控制方程。
39.针对具体的网格移动速度场则需要通过求解ω(t)上的泊松方程得到：
其中
∂
ω
imp
(t)表示具有网格移动速度或位移的边界，
∂
ω\
∂
ω
imp
(t)是固定边界。也可以在域内定义网格位移或者固定网格。
40.张量λ通常被定义为单位矩阵，也可以定义各向异性的张量λ以使网格在特定方向和给定区域中具有更强的刚性。但是，具有各向异性的λ会导致网格速度v的分量之间存在强耦合。
41.水轮机启停工况下，由活动导叶开度变化造成流体域几何结构变化，在此动网格算法的基础上，只需确定活动导叶边界面上网格移动的速度，就能得到网格移动的全场解，实现网格变化。
42.一般情况下，一台水轮机具有20片活动导叶，以圆周均匀间隔的方式分布在导水区。每片导叶都有固定的旋转轴，首先定位旋转轴的坐标 (x0, y0, 0) ，再获取边界面上的网格位置信息(xn, yn, zn)。一般情况下，活动导叶的旋转为竖直方向即z轴，故保持z不变考虑平面转动即可。进行坐标变化，将坐标原点变为旋转中心，其计算公式如下：距旋转中心的距离r和与x轴的夹角θ为：在转动角速度为ω的情况下，点(xn, yn, zn)转动速度为：在计算流体力学cfd模型求解中，通过使用udf（用户自定义函数）的方法，确定网格运动的边界条件，确定每个网格节点的运动速度，其具体包括以下内容：首先使用获取网格坐标的函数，获得边界面上网格位置信息；再对边界面上的网格节点做循环，使用上述方法依次计算距旋转中心的距离r和
与x轴的夹角θ，再根据转动速度公式，计算节点的运动速度，最终确定边界面网格的运动速度。
43.本发明充分考虑现有技术中针对预测水轮机启停工况流场状态的需求，以及数值模拟存在的难题：如何准确描述以及计算启停工况下，导叶开度变化导致的流体域几何模型变化。
44.进而，本发明构建若干模型，可以根据水轮机启停工况下活动导叶运动过程，确定网格运动方式，在计算过程中，流体域网格几何形状自动变化，以匹配真实的物理状况。在确定网格运动时，只需要确定边界面处的网格移动，通过使用任意拉格朗日-欧拉方法，求解网格运动守恒方程，得到全局网格节点的运动信息。
45.本发明计算流体力学cfd模型的一种具体实施例：计算流体力学cfd模型根据流体力学控制方程进行构建。
46.流体力学控制方程包括质量守恒和动量守恒方程，其具体的计算公式如下:其中为流体速度、ρ为流体密度、为应力场、为体积力源项（如重力）。
47.接下来对流体力学控制方程进行时间和空间上的离散。
48.该计算流体力学cfd模型使用有限体积方法进行计算，通过对网格单元进行积分，确定外延量，其计算公式如下：其中，为单元体积，为单元质量，为单元动量。
49.对δt（第n步到第n+1步，一个时间步）的积分计算公式如下：
其中，（.）n表示第n时间步的物理量。
50.对质量守恒方程进行时间上的离散，其计算公式如下：对动量守恒方程进行时间上的离散，其计算公式如下：对空间上的离散，选择cfd常用的有限体积方法离散方程，首先使用显式压力场进行速度预测，再进行一个校正计算，其中连续性方程用于计算压力的变化。
51.校正步骤调整质量通量以确保质量守恒，然后更新速度场。
52.本发明网格运动求解方法的一种具体实施例：网格运动求解方法包括以下内容：首先，在计算流体力学cfd模型中添加动网格模型，该动网格模型添加在速度场求解之后。
53.然后求解ωn域上的预测速度并得到修正后的速度场u
cn+1,k
后（n为当前时间步，n+1为下一时间步，k为当前迭代步）。
54.再根据用户输入的网格位移边界条件求解网格运动的三个控制方程和泊松方程，得到网格运动的全场解vc|
nn+1,k
。
55.最后，根据网格运动的全场解，重构出每个网格节点的速度vf|
nn+1,k
，由此得到每个节点的位移，构建出网格运动后的求解域ω
n+1
。
56.本发明应用在如图3所示的francis 99混流式水轮机上的一种具体实施例：一种应用在francis 99混流式水轮机的启停工况流场预测方法，包括以下内容：步骤1：构建水轮机流体域全流道的cad模型。由于水轮机结构复杂，需要根据详细的工程图，构建出准确的cad模型。在cad模型的基础上，使用网格生成技术，对几何体分块，生成结构化的网格模型，并根据将要选用的湍流模型对第一层网格y+要求，设置壁面网格厚度。
57.步骤2：将网格模型导入计算流体力学cfd模型，根据启停工况参数确定边界条件。该步骤需要获取启停工况下，入口流量和出口压力随时间变化的值。同时，使用旋转机械模块，用以模拟转子-定子间的相互作用。在该模块下，确定转轮区域的旋转轴以及启停工况下，随时间变化的转轮转速。
58.步骤3：根据导叶在启停工况下的运动规律，确定导叶边界面上的网格移动速度，并在每片导叶的边界面上确定一个边界条件，其具体包括内容：首先，确定每片导叶旋转轴的坐标，在遍历边界面上的网格单元的坐标信息，使用
绕轴旋转公式，确定叶片绕轴旋转的方向。并根据启停工况下的导叶转动速率变化确定随时间变化的转速。该部分可以使用udf（用户自定义函数）完成。
59.根据本发明描述的叶片旋转计算公式，首先确定一片叶片的旋转中心(x0, y0, 0)，再遍历该叶片上的所有边界面单元，获取每个边界面单元的中心坐标(xn, yn, zn)。
60.通过公式计算得到边界面相对于旋转中心的坐标，由此得到边界面距旋转中心的距离和相对于x轴的夹角，其计算公式如下：假设导叶转动速度为ω，则确定每个边界面单元的网格运动速度为：以此类推，根据每个叶片的旋转中心，确定所有叶片边界面网格的旋转速度。
61.步骤4：最后完成数值计算相关参数设置，湍流模型选择k-ω sst、时间步长设置为δt=1*10-5
s、离散方式选择二阶中心差分，求解精度设置为1*10-8
。确定完所有数值参数后，使用计算流体力学cfd模型运算。
62.在计算结束后，获得整个启停工况的全场解。
63.本发明运维过程的一种具体实施例：首先，确定尾水管测点的位置，使用后处理软件，获得测点位置的压力变化信息。
64.再以速度云图形式显示结果，使用后处理软件的播放功能，观察在整个启停工况下，内流场的状态变化，以及尾水管涡带的形成、增强和消失。
65.最后结合压力脉动信息，分析获取压力脉动最为剧烈的工况区间，指导运维人员尽量避免该工况。
66.应用本发明方法的一种装置实施例：一种计算机设备，其包括：一个或多个处理器；存储装置，用于存储一个或多个程序；当所述一个或多个程序被所述一个或多个处理器执行时，使得所述一个或多个处理器实现上述的一种水轮机启停工况流场仿真预测方法。
67.应用本发明方法的一种计算机介质实施例：一种计算机可读存储介质，其上存储有计算机程序，该程序被处理器执行时实现上述的一种水轮机启停工况流场仿真预测方法。
68.本领域内的技术人员应明白，本技术的实施例可提供为方法、系统、或计算机程序
产品。因此，本技术可采用完全硬件实施例、完全软件实施例、或结合软件和硬件方面的实施例的形式。而且，本技术可采用在一个或多个其中包含有计算机可用程序代码的计算机可用存储介质（包括但不限于磁盘存储器、cd-rom、光学存储器等）上实施的计算机程序产品的形式。
69.本技术是参照根据本技术实施例的方法、设备（系统）、和计算机程序产品的流程图和／或方框图来描述的。应理解可由计算机程序指令实现流程图和／或方框图中的每一流程和／或方框、以及流程图和／或方框图中的流程和／或方框的结合。可提供这些计算机程序指令到通用计算机、专用计算机、嵌入式处理机或其他可编程数据处理设备的处理器以产生一个机器，使得通过计算机或其他可编程数据处理设备的处理器执行的指令产生用于实现在流程图一个流程或多个流程和／或方框图一个方框或多个方框中指定的功能的装置。
70.最后应当说明的是：以上实施例仅用以说明本发明的技术方案而非对其限制，尽管参照上述实施例对本发明进行了详细的说明，所属领域的普通技术人员应当理解：依然可以对本发明的具体实施方式进行修改或者等同替换，而未脱离本发明精神和范围的任何修改或者等同替换，其均应涵盖在本发明的权利要求保护范围之内。