一种无人自行车几何结构参数优化方法

1.本发明涉及无人自行车技术领域，具体涉及一种无人自行车几何结构参数优化方法。


背景技术：

2.无人自行车是一种可在狭长道路上自主实现平衡运动的新型智能驾驶交通工具。平衡稳定速度范围是自行车性能考核的重要指标，其一方面受控制器的影响，另一方面还与轴距、车把前倾角、后偏距、车轮半径等几何结构参数密切相关。目前，无人自行车研究领域尚缺少对无人自行车几何结构参数进行合理优化的理论方法，因此，在原理上给出一种量化描述无人自行车几何结构参数对系统平衡特性影响的动态模型，并在工程实践中将其用于系统关键结构参数的优化，具有重要的理论意义和实际价值。已有的文献研究表明，线性变参数(linear variable parameter，lpv)力学模型是一种经典的无人自行车模型，可以较为简洁有效地诠释无人自行车几何结构参数和实时的运动参数的二阶动态响应关系，被广泛地应用于无人自行车研究领域，尤其是系统特性分析和平衡控制器设计中。然而，迄今为止，鲜有研究人员注意到可以利用该模型对其中隐含的几何结构参数进行合理地选择优化。


技术实现要素：

3.本发明提供一种无人自行车几何结构参数优化方法，用于优化无人自行车机械结构，以便提高其平衡稳定速度范围。
4.为解决上述问题，本发明通过以下技术方案实现：
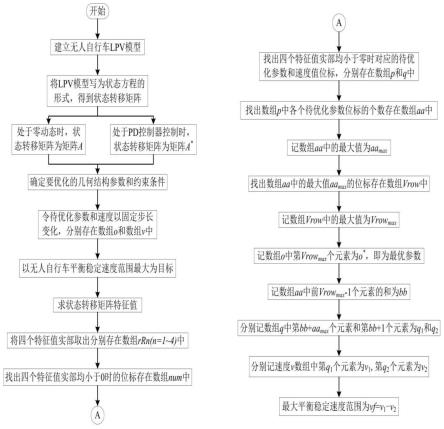
5.一种无人自行车几何结构参数优化方法，包括如下步骤：
6.步骤1、建立无人自行车lpv模型：
[0007][0008]
选取状态变量，将lpv模型表达式写为状态方程的形式，得到状态转移矩阵：
[0009][0010][0011][0012][0013]
1)当无人自行车处于零动态时，以矩阵a为状态转移矩阵；
[0014]
2)当无人自行车处于pd控制器控制时，以矩阵a
*
为状态转移矩阵；
[0015]
步骤2、确定要优化的几何结构参数和约束条件，求解状态转移矩阵特征值，以无人自行车平衡稳定速度范围最大为目标；
[0016]
步骤3a、当无人自行车处于零动态时，通过分析其状态转移矩阵a的特征值负实部与待优化参数的取值关系，求得目标下的最优参数；
[0017]
步骤3b、当无人自行车处于pd控制器控制时，通过分析其状态转移矩阵a
*
的特征值负实部与待优化参数的取值关系，求得目标下的最优参数；
[0018]
步骤4、验证优化结果的可靠性。
[0019]
上述步骤1中，m是质量矩阵；c是“阻尼”矩阵；k是刚度矩阵；k是刚度矩阵；δ分别是车架横滚角和车把转角；分别是q在时间域上的一阶导数和二阶导数； f＝[0 τ]
t
，τ为车把力矩。
[0020]
状态变量状态变量是状态变量x在时间域上的一阶导数；输入变量u＝τ(零动态时τ＝0，pd控制器控制时τ＝-kx，k为pd控制器参数)；矩阵矩阵
[0021]
上述步骤2中，根据控制工程原理当状态方程中状态转移矩阵特征值实部均小于零时即认为系统稳定，则状态转移矩阵特征值实部均小于零时对应的速度范围即为无人自行车平衡稳定速度范围。
[0022]
与现有技术相比，本发明具有如下特点：
[0023]
1.本发明通过借助lpv模型，对无人自行车状态转移矩阵特征值进行分析，定量表征了无人自行车几何结构参数和其平衡稳定速度范围的内在联系，具有严谨可靠的理论基础。
[0024]
2.通过以无人自行车平衡稳定速度范围最大为目标，分析其状态转移矩阵的特征值负实部与待优化参数的取值关系，求得目标下的最优参数，实现了对无人自行车几何结构参数进行优化的目标，工程意义明显。
附图说明
[0025]
图1是本发明的流程图。
[0026]
图2为无人自行车机械结构简图，其中h、b、r、f是组成无人自行车的四个刚体，分别为车把、车架、后车轮、前车轮；w为轴距、α为车把前倾角、c为后偏距、r为车轮半径。
[0027]
图3中图(a)和图(b)分别为实例一中零动态时以无人自行车平衡稳定速度范围最大为目标下的非最优轴距w和最优轴距w
*
对应的无人自行车平衡稳定速度范围(图中阴影部分)图；图中实线为特征值实部re(λ)曲线，虚线为特征值虚部im(λ)曲线，下同。
[0028]
图4中图(a)和图(b)分别为实例一中零动态时以无人自行车平衡稳定速度范围最大为目标下的非最优车把前倾角α和最优车把前倾角α
*
对应的无人自行车平衡稳定速度范围图。
[0029]
图5中图(a)和图(b)分别为实例一中零动态时以无人自行车平衡稳定速度范围最大为目标下的非最优后偏距c和最优后偏距c
*
对应的无人自行车平衡稳定速度范围图。
[0030]
图6中图(a)和图(b)分别为实例一中零动态时以无人自行车平衡稳定速度范围最大为目标下的非最优车轮半径r和最优车轮半径r
*
对应的无人自行车平衡稳定速度范围图。
[0031]
图7中图(a)和图(b)分别实例二以pd控制器控制时以无人自行车平衡稳定速度范围最大为目标下的非最优轴距w和最优轴距w
*
对应的无人自行车平衡稳定速度范围图。
[0032]
图8中图(a)和图(b)分别为实例二以pd控制器控制时以无人自行车平衡稳定速度范围最大为目标下的非最优车把前倾角α和最优车把前倾角α
*
对应的无人自行车平衡稳定速度范围图。
[0033]
图9中图(a)和图(b)分别为实例二以pd控制器控制时以无人自行车平衡稳定速度范围最大为目标下的非最优后偏距c和最优后偏距c
*
对应的无人自行车平衡稳定速度范围图。
[0034]
图10中图(a)和图(b)分别为实例二以pd控制器控制时以无人自行车平衡稳定速度范围最大为目标下的非最优车轮半径r和最优车轮半径r
*
对应的无人自行车平衡稳定速度范围图。
具体实施方式
[0035]
为使本发明的目的、技术方案和优点更加清楚，下面以无人自行车轴距w、车把前倾角α、后偏距c、车轮半径r作为优化对象并结合多种情况下的具体实例，对本发明做进一步详细说明。
[0036]
实例一：当无人自行车处于零动态时，对无人自行车的轴距w、车把前倾角α、后偏距c、车轮半径r进行优化。
[0037]
首先对轴距进行优化，步骤如下：
[0038]
步骤1、建立无人自行车lpv模型：
[0039][0040]
式中，m
11
、m
12
、m
21
、m
22
、c
11
、c
12
、c
21
、c
22
、k
11
、k
12
、k
21
、k
22
是与无人自行车lpv 模型参数有关的且含有待优化参数的常系数。
[0041]
以车架横滚角车把转角δ、车架横滚角速度和车把转角速度为状态变量，将 lpv模型写成状态方程的形式，得到含有待优化参数轴距w的状态转移矩阵a：
[0042][0043]
式中，状态变量输入变量u＝τ，零动态时系统输入τ＝0；状态转移矩阵输入矩阵
[0044]
步骤2、以无人自行车轴距为优化对象，考虑到轴距应大于前轮半径和后轮半径之和，且轴距不应过长，则以w＝0.6m～2m为轴距寻优范围，以无人自行车平衡稳定速度范围最大为目标。
[0045]
令无人自行车轴距w和速度v分别在w
min
～w
max
和v
min
～v
max
范围内均匀变化，步长为δw，δv。求状态转移矩阵a的特征值，进而求出无人自行车平衡稳定最大速度范围。具体步骤如下：
[0046]
1)令轴距和速度分别在w
min
～w
max
和v
min
～v
max
范围内以固定步长变化，分别存在数组w和数组v中；
[0047]
2)求得状态转移矩阵a的特征值，并将四个特征值的实部取出分别存在数组rrn (n＝1～4)中；
[0048]
3)找出状态转移矩阵a的四个特征值实部均小于零时的位标存在数组num中；
[0049]
4)找出四个特征值实部均小于零时对应的轴距和速度值位标，分别存在数组p和q 中：
[0050]
数组p中的各个元素p(i)由num(i)/l向上取整得到，数组q中的各个元素 q(i)＝num(i)-(p(i)-1)*l，其中i＝1～j，j是数组num中元素的个数，是速度v数组中元素的个数；
[0051]
5)找出数组p中各个轴距位标的个数存在数组aa中；
[0052]
6)找出数组aa中的最大值记为aa
max
；
[0053]
7)找出数组aa中最大值aa
max
的位标并存在数组vrow中，并记数组vrow中的最大值为vrow
max
；
[0054]
8)求数组aa中前vrow
max-1个元素的和记为bb；
[0055]
9)找出无人自行车最大平衡稳定速度范围中的最大速度和最小速度对应的位标，分别记为q1和q2：
[0056]
q1为数组q中第bb+aa
max
个元素，q2为数组q中第bb+1个元素；
[0057]
10)分别取速度v数组中第q1个和第q2个元素记为v1和v2，vf＝v
1-v2即为无人自行车最大的平衡稳定速度范围。
[0058]
上述中，w
min
，w
max
分别为0.6m和2m；v
min
，v
max
分别为0m/s和10m/s；δw，δv均为0.01。
[0059]
步骤3、基于步骤2中对状态转移矩阵a特征值负实部与轴距取值关系的分析，求得最大平衡稳定速度范围所对应的轴距。取轴距w数组中第vrow个元素记为w
*
，即为该目标下的最优轴距。对于本实例w
*
＝0.78m。
[0060]
步骤4、如附图3中图(a)所示，图中阴影部分所对应的速度范围是非最优轴距w对应的无人自行车平衡稳定速度范围。图(b)中的阴影部分所对应的速度范围是最优轴距w
*
对应的无人自行车平衡稳定速度范围。具体见下表：
[0061]
速度w＝0.64mw＝0.71mw
*
＝0.78mw＝0.85mw＝0.92mv1(m/s)1010105.744.21v2(m/s)5.094.413.953.633.91vf(m/s)4.915.596.052.110.30
[0062]
注：v1和v2分别是各轴距对应的无人自行车平衡稳定速度的最大值和最小值； vf＝v
1-v2，是各轴距对应的无人自行车平衡稳定速度范围，即图中阴影部分对应的速度范围。
[0063]
为使上述步骤2和步骤3更加清楚，现举例如下：
[0064]
令w
min
＝0.8，w
max
＝0.9；v
min
＝3.6m/s，v
max
＝3.7m/s；δw＝0.01m，δv＝0.05m/s，在此范围内对无人自行车轴距进行优化，具体如下：
[0065]
步骤2中，求无人自行车最大的平衡稳定速度范围，如下：
[0066]
1)求状态转移矩阵a的特征值：
[0067]
轴距w/m：
[0068]
数值0.800.810.820.830.840.850.860.870.880.890.90位标1234567891011
[0069]
速度v/(m/s)：
[0070]
数值3.603.656.70位标123
[0071]
第一个特征值的实部rr1：
[0072]
数值-9.0062-9.1180-9.2299-8.9303-9.0408-9.1514-8.8401-8.9492位标12345678-9.0583-8.7353-8.8427-8.9502-8.6158-8.7215-8.8272-8.4819-8.585791011121314151617-8.6896-8.3347-8.4364-8.5383-8.1752-8.2749-8.3745-8.0054-8.1028181920212223242526-8.2002-7.8273-7.9223-8.0173-7.6435-7.7361-7.8286
ꢀꢀ
27282930313233
ꢀꢀ
[0073]
第二个特征值的实部rr2：
[0074][0075][0076]
第三个特征值的实部rr3：
[0077]
数值0.17220.12860.08830.13450.09280.0540.09970.0598位标123456780.02270.06840.0304-0.00490.04150.0055-0.0280.0199-0.014191011121314151617-0.04580.0046-0.0273-0.0571-0.0035-0.0332-0.0611-0.0032-0.0308181920212223242526-0.05670.0062-0.0192-0.04300.02560.0025-0.0192
ꢀꢀ
27282930313233
ꢀꢀ
[0078]
第四个特征值的实部rr4：
[0079]
数值-0.8625-0.7959-0.7356-0.8009-0.7383-0.6816-0.7399-0.6812位标12345678-0.6283-0.6796-0.6249-0.5756-0.6201-0.5694-0.5237-0.5615-0.514791011121314151617-0.4725-0.5040-0.4610-0.4222-0.4475-0.4082-0.3726-0.3921-0.3563
181920212223242526-0.3239-0.3378-0.3053-0.2758-0.2845-0.2551-0.2286
ꢀꢀ
27282930313233
ꢀꢀ
[0080]
2)四个特征值实部均为负值时的位标数组num：
[0081]
数值121517182021222324252627293033位标123456789101112131415
[0082]
3)四个特征值实部均为负值时的轴距位标数组p：
[0083]
数组456677888999101011位标123456789101112131415
[0084]
四个特征值实部均为负值时的速度位标数组q：
[0085]
数值332323123123233位标123456789101112131415
[0086]
4)找出数组p中各个轴距位标的个数并存在数组aa中：
[0087]
轴距位标1234567891011aa00011223321
[0088]
5)数组aa中的最大值aa
max
＝3。
[0089]
6)数组aa中的最大值aa
max
对应的轴距的位标存在数组vrow中：
[0090]
vrow89
[0091]
数组vrow中的最大值vrow
max
＝9。
[0092]
7)求数组aa中前vrow
max-1个元素的和记为bb，bb＝9。
[0093]
8)q1为数组q中第bb+aa
max
个元素，q2为数组q中第bb+1个元素，则q1＝3，q2＝1。
[0094]
9)分别取速度v数组中第q1个和第q2个元素记为v1和v2，vf＝v
1-v2即为最大平衡稳定速度范围，则v1＝3.7m/s，v2＝3.6m/s，vf＝v
1-v2＝3.7-3.6＝0.1m/s。
[0095]
步骤3中取轴距w数组中第vrow个元素，即为无人自行车平衡稳定最大速度范围对应的轴距，记为w
*
：
[0096]
*0.87m0.88m
[0097]
同理，可对无人自行车的车把前倾角α、后偏距c、车轮半径r进行优化，其条件和结果如下：
[0098]
(1)对车把前倾角α进行优化。
[0099]
条件：α
min
＝5
°
，α
max
＝35
°
；v
min
＝0m/s，v
max
＝10m/s；δα＝1
°
，δv＝0.01m/s。
[0100]
结果：α
*
＝20
°
。最优车把前倾角α
*
和非最优车把前倾角α对应的无人自行车平衡稳定速度范围对比图如图4中图(a)图(b)所示，具体见下表：
[0101]
速度α＝12
°
α＝16
°
α
*
＝20
°
α＝24
°
α＝28
°
v1(m/s)4.334.875.395.886.37v2(m/s)3.853.614.024.625.41vf(m/s)0.481.261.371.260.96
[0102]
注：v1和v2分别是各车把前倾角对应的无人自行车平衡稳定速度的最大值和最小
值； vf＝v
1-v2，是各车把前倾角对应的无人自行车平衡稳定速度范围，即图中阴影部分对应的速度范围。
[0103]
(2)对后偏距c进行优化。
[0104]
条件：c
min
＝0m，c
max
＝0.25m；v
min
＝0m/s，v
max
＝10m/s；δc＝0.01m，δv＝0.01m/s。
[0105]
结果：对后偏距的优化有两个最优解，分别为c
*
＝0.24m和c
*
＝0.25m，且二者对应的无人自行车平衡稳定速度范围一致。最优后偏距c
*
和非最优后偏距c对应的无人自行车平衡稳定速度范围对比图如图5中图(a)图(b)所示，具体见下表：
[0106]
速度c＝0.04mc＝0.09mc＝0.14mc＝0.19mc
*
＝0.24mc
*
＝0.25mv1(m/s)4.085.176.84101010v2(m/s)3.883.563.423.343.283.28vf(m/s)0.201.613.426.666.726.72
[0107]
注：v1和v2分别是各后偏距对应的无人自行车平衡稳定速度的最大值和最小值； vf＝v
1-v2，是各后偏距对应的无人自行车平衡稳定速度范围，即图中阴影部分对应的速度范围。
[0108]
由上表可知，后偏距在0.19m-0.25m范围内，无人自行车平衡稳定速度范围差别较小，则可根据装配条件等其他要求在此范围内选择合适的值作为最终的最优解。
[0109]
(3)对车轮半径r进行优化。
[0110]
条件：r
min
＝0m，r
max
＝0.8m；v
min
＝0m/s，v
max
＝10m/s；δr＝0.01m，δv＝0.01m/s。
[0111]
结果：对车轮半径的优化有两个最优解，分别为r
*
＝0.52m和r
*
＝0.53m，二者对应的无人自行车平衡稳定速度范围略有差别。他们的最优车轮半径r
*
和非最优车轮半径r对应的无人自行车平衡稳定速度范围对比图如图6中图(a)图(b)所示，具体见下表：
[0112]
速度r＝0.23mr＝0.33mr＝0.43mr
*
＝0.52mr
*
＝0.53mr＝0.63mv1(m/s)4.165.285.257.347.458.53v2(m/s)3.243.833.705.335.447.19vf(m/s)0.921.451.552.012.011.34
[0113]
注：v1和v2分别是各车轮半径对应的无人自行车平衡稳定速度最大值和最小值；vf＝v
1-v2，是各车轮半径对应的无人自行车平衡稳定速度范围，即图中阴影部分对应的速度范围。
[0114]
实例二：当无人自行车处于pd控制器控制时，对无人自行车的轴距w、车把前倾角α、后偏距c、车轮半径r进行优化。
[0115]
首先对轴距进行优化，步骤如下：
[0116]
步骤1、建立无人自行车lpv模型：
[0117][0118]
式中，m
11
、m
12
、m
21
、m
22
、c
11
、c
12
、c
21
、c
22
、k
11
、k
12
、k
21
、k
22
是与无人自行车lpv 模型参数有关且含有待优化参数的常系数。
[0119]
同样以车架横滚角车把转角δ、车架横滚角速度和车把转角速度为状态变量，将lpv模型写成状态方程的形式，得到含有待优化参数轴距w的状态转移矩阵a
*
：
[0120][0121][0122][0123][0124]
式中，状态变量输入变量u＝τ，pd控制器控制下的系统输入τ＝-kx，选择合适的pd控制器参数，本实例中k＝[-20 0 8 0]；矩阵矩阵
[0125]
步骤2、以无人自行车轴距为优化对象，同样以w＝0.6m～2m为轴距寻优范围，构造以pd控制器控制下的平衡稳定速度范围最大为目标。
[0126]
令无人自行车轴距w和速度v分别在w
min
～w
max
和v
min
～v
max
范围内均匀变化，步长为δw，δv。求矩阵a
*
的特征值，进而求出无人自行车平衡稳定最大速度范围。具体步骤如下：
[0127]
1)令轴距和速度分别在w
min
～w
max
和v
min
～v
max
范围内以固定步长变化，分别存在数组w和数组v中；
[0128]
2)求得矩阵a
*
的特征值，并将四个特征值的实部取出分别存在数组rrn(n＝1～4) 中；
[0129]
3)找出矩阵a
*
的四个特征值实部均小于零时的位标存在数组num中；
[0130][0131]
其余步骤与实例一中的相同，此处不再赘述。
[0132]
上述中，w
min
，w
max
分别为0.6m和2m；v
min
，v
max
分别为0m/s和10m/s；δw，δv均为0.01。
[0133]
步骤3、基于步骤2中对状态转移矩阵a
*
特征值负实部与轴距取值关系的分析，求得最大平衡稳定速度范围所对应的轴距。取轴距w数组中第vrow个元素记为w
*
，即为该目标下的最优轴距。对于本实例w
*
＝0.95m。
[0134]
步骤4、如附图7中图(a)所示，图中阴影部分所对应的速度范围是非最优轴距w对应的无人自行车平衡稳定速度范围。图(b)中的阴影部分所对应的速度范围是最优轴距w
*
对应的无人自行车平衡稳定速度范围。具体见下表：
[0135]
速度w＝0.65mw＝0.75mw＝0.85mw
*
＝0.95mw＝0.97mv1(m/s)101010100.97v2(m/s)0.850.700.550.360.33vf(m/s)9.159.309.459.640.64
[0136]
注：v1和v2分别是各轴距对应的无人自行车平衡稳定速度的最大值和最小值； vf＝v
1-v2，是各轴距对应的无人自行车平衡稳定速度范围，即图中阴影部分对应的速度范围。
[0137]
同理，可对无人自行车的车把前倾角α、后偏距c、车轮半径r进行优化，其优化条件
和结果如下：
[0138]
(1)对车把前倾角α进行优化。
[0139]
条件：α
min
＝5，α
max
＝35
°
；v
min
＝0m/s，v
max
＝10m/s；δα＝1
°
，δv＝0.01m/s。
[0140]
结果：α
*
＝16
°
。最优车把前倾角α
*
和非最优车把前倾角α对应的无人自行车平衡稳定速度范围对比图如图8中图(a)图(b)所示，具体见下表：
[0141]
速度α＝6
°
α＝11
°
α
*
＝16
°
α＝21
°
α＝26
°
v1(m/s)0.5010101010v2(m/s)0.470.510.480.771.23vf(m/s)0.039.499.529.238.77
[0142]
注：v1和v2分别是各车把前倾角对应的无人自行车平衡稳定速度的最大值和最小值； vf＝v
1-v2，是各车把前倾角对应的无人自行车平衡稳定速度范围，即图中阴影部分对应的速度范围。
[0143]
(2)对后偏距c进行优化。
[0144]
条件：c
min
＝0m，c
max
＝0.25m；v
min
＝0m/s，v
max
＝10m/s；δc＝0.01m，δv＝0.01m/s。
[0145]
结果：最优后偏距c
*
可取0.01m、0.02m、0.03m、0.04m多个值，且它们对应的无人自行车平衡稳定速度范围一致。最优后偏距c
*
和非最优后偏距c对应的无人自行车平衡稳定速度范围对比图如图9中图(a)图(b)所示，具体见下表：
[0146]
速度c＝0mc
*
c＝0.11mc＝0.18mc＝0.25mv1(m/s)4.0210101010v2(m/s)0.470.450.540.680.82vf(m/s)3.559.559.469.329.18
[0147]
注：v1和v2分别是各后偏距对应的无人自行车平衡稳定速度的最大值和最小值； vf＝v
1-v2，是各后偏距对应的无人自行车平衡稳定速度范围，即图中阴影部分对应的速度范围。
[0148]
(3)对车轮半径r进行优化。
[0149]
条件：r
min
＝0m，r
max
＝0.8m；v
min
＝0m/s，v
max
＝10m/s；δr＝0.01m，δv＝0.01m/s。
[0150]
结果：车轮半径在0.1m～0.8m的范围内无人自行车平衡稳定速度范围呈缓慢递减的趋势。各半径值对应的无人自行车平衡稳定速度范围对比图如图10中图(a)图(b)所示，具体见下表：
[0151]
速度r＝0.1mr＝0.2mr＝0.3mr＝0.4mr＝0.5mr＝0.6mr＝0.7mr＝0.8mv1(m/s)1010101010101010v2(m/s)0.450.470.480.530.580.650.730.85vf(m/s)9.559.539.529.479.429.359.279.15
[0152]
注：v1和v2分别是各车轮半径对应的无人自行车平衡稳定速度的最大值和最小值； vf＝v
1-v2，是各车轮半径对应的无人自行车平衡稳定速度范围，即图中阴影部分对应的速度范围。
[0153]
上述实例中无人自行车lpv模型各参数来自于一辆现有的无人自行车物理样机，具体见表1。
[0154]
表1实例中研究对象lpv模型各参数值
[0155][0156]
在上述两个实例中，借助lpv模型针对零动态和pd控制器控制两种情况，以无人自行车平衡稳定速度范围最大为目标，通过对状态转移矩阵a(a
*
)特征值负实部与待优化参数取值关系的分析，求得目标下的最优参数，实现了对其轴距w、车把前倾角α、后偏距c、车轮半径r等多种几何结构参数的优化。结果表明，在相同条件下，采用本发明的几何结构参数优化结果，能够有效提高无人自行车的平衡稳定速度范围，即达到了对无人自行车几何结构参数优化的目标，具有重要的工程意义。
[0157]
上述实例，仅为对本发明的目的、技术方案等做进一步详细说明的具体个例，但本发明并非限定于此。凡在本发明公开的范围之内所做的任何修改、等同替换、改进等，均包含在本发明的保护范围之内。