同步反演高分辨率人为CO2排放与自然CO2通量的同化方法及系统

同步反演高分辨率人为co2排放与自然co2通量的同化方法及系统
技术领域
1.本发明涉及大气科学、地理科学、全球变化科学技术领域，特别是涉及一种同步反演高分辨率人为co2排放与自然co2通量的同化方法及系统。


背景技术：

2.为了科学评价碳中和各项政策和各项计划实施的有效性，急需甄别人为co2排放和自然co2通量的方法技术。量化全球和区域co2通量非常重要。陆地生态系统复杂多样、观测数据时空尺度和精度上差异大等原因导致各种方法估算的陆地生态系统co2源汇不确定性大(piao et al., 2012；schimel et al.，2015；arneth et al.,2017；bastos et al.,2020)。通过全球和区域尺度co2收支估算不确定性的评价(bastos et al.,2020； le qu
éré
et al.,2018)发现，区域尺度上的不确定性相对于全球尺度要大(martin et al.,2019；hutchins et al.,2017；fischer et al.,2017； gately and hutyra,2017；oda et al.,2018)。未来减排决策和缓解气候变化策略的制定中离不开高精度、高分辨率co2源汇信息。因此，降低co2源汇估算的不确定性，提高co2通量的反演精度是全球变化研究的热点之一 (pillai et al.，2016；turnbull et al.，2015；ye et al.，2018；wanget al.,2019；oda et al.，2018；wang et al.,2020)。
3.当前co2通量的估算方法包括基于陆地观测的“自下而上(bottom-up)”方法(于贵瑞等,2011；tian et al.,2011；刘纪远等,2003； asefi-najafabady et al.,2014；jiang et al.,2016；kondo et al.,2020) 和基于大气观测的“自上而下(top-down)”方法(peters et al.,2007； deng et al.,2016；zhang et al.,2014；peng et al.,2015；wang etal.,2019；smith et al.,2020；陈报章，张慧芳，2015)。“自上而下”的方法已成为目前co2循环研究的主流方向(peters et al.,2005,2007； zhang et al.,2014；tian et al.,2014；peng et al.,2015；wang etal.,2019)。自上而下的方法受观测数据数量和模型效率等因素的制约，其反演结果分辨率低、不确定性大(br
é
on et al.,2015)。此外，大部分co2通量同化反演方法是在假定自然或人为co2通量的其中一方不存在误差的前提下去优化另一方，这种假设一定程度上增加所反演的co2通量的不确定性并降低了其应用价值。传统上采用自下而上的物料平衡方法估算国家和行政单元尺度人为co2的年总排放量，但该方法存在不确定性大且滞后性明显的问题。因此，迫切需要发展区域大气co2反演法，以实现自然co2通量和人为co2排放的在线同步反演核算。
4.早期的大气反演模型并不是为估算人为碳排放而设计和开发的，而是在假设人为碳排放无误差(模型中固定不变)的情况下，利用大气co2浓度观测来优化陆地或海洋自然co2通量(peters et al.,2007,2010；jianget al.,2016；saeki et al.,2013；zhang et al.,2014)。这种“人为碳排放无误差”假设存在着很大的缺陷性，因为大气co2浓度变化是近地表自然和人为碳通量经过大气混合后的结果，设定人为碳排放无误差(实际上基于调查清单法估算出的人为co2排放存在着极大的不确定性)必定会增大自然碳通量(陆地或海
洋)估算的不确定性(gurney et al.,2005)。近期有研究者尝试应用大气碳反演系统计算人为co2排放量，其做法是：因为大气co2浓度变化主要受“自然co2通量”和“人为碳排放”影响，因此在假定存在一个具有相同“自然co2通量”而没有“人为co2排放”的背景区(background region)存在的前提下，利用背景区剔除自然co2通量的影响，计算出大气co2浓度增量
△
co2。在理论上，
△
co2被认为是由人为co2排放量导致的是合理的。这样就可以通过降低模拟和观测的co2浓度差值来纠正人为co2排放估算的误差(kort et al.,2012；schneising et al.,2013； wong et al.,2015；br
é
on et al.et al.2015；pillai et al.,2016； martin et al.,2019)。选定一块自然条件相似(有相似的自然生态系统碳通量)而人烟稀少(近似本地人为源排放为0)的背景区来计算co2浓度增量(
△
co2)，以区分出人为碳排放。这种改进后的大气co2反演法被称之为一种人为碳排放反演法(kort et al.2012；schneising et al.2013； wong et al.2015；br
é
on et al.et al.2015；pillai et al.2016；yeet al.2020)。采用该方法已成功反演出法国(staufer et al.et al.2016)、洛杉矶(wong et al.,2015)、柏林(hase et al.,2015)、韩国(shim et al. 2019)和北京(feng et al.,2019)等城市人为co2排放。但这种不受人为co2排放影响的理想背景区的“假设”条件在地球上很难找到，实际上很难找到绝对的“背景区”来计算人为碳源导致的co2浓度增量。因此，这种方法的应用价值十分有限。目前基于大气反演模型达到方法估算人为碳排放的结果仍存在着很大的不确定性，而且不能区分自然co2通量和人为co2排放，这是评估碳中和行动有效性急需解决的技术问题。


技术实现要素：

5.本发明要解决的技术问题是提供一种同步反演高分辨率人为co2排放与自然co2通量的同化方法及系统，能够解决其无法区分人为co2排放和自然co2通量的技术难题。
6.为解决上述技术问题，本发明提供了一种同步反演高分辨率人为co2排放与自然co2通量的同化方法，所述方法包括：解析遥感影像数据 modiso9a1数据，产生增强型植被指数和地表水指数数据集作为vprm输入数据；制备先验人为co2排放、生物质燃烧的数据，驱动wrf-ghg模型前向模拟co2浓度场和自然co2通量场；基于所设置的模型模拟区域范围内的co2通量观测数据，对wrf-ghg模型模拟的自然co2通量结果进行优化，并对嵌套于wrf-ghg模型中的自然生态co2诊断模型vprm模块进行参数优化；基于尺度匹配后的地基和多源卫星co2浓度数据，采用pod4dvar数据同化算法，实现地基-多源卫星联合同化，进而实现对人为co2排放的反演核算；生成区域高时空分辨率数据产品集，区域高时空分辨率数据产品集包括： co2浓度场、自然co2通量场、人为co2碳排放场；对4维的区域高时空分辨率数据产品集进行准确性验证和模型鲁棒性验证；构建区域碳同化反演系统，实现同步同化目标区域高分辨、高精度人为co2排放与自然co2通量。
7.在一些实施方式中，对vprm模块进行的参数优化包括：数据质量控制；根据站点通量足迹模型剔除周边人为源对通量观测数据产生较大影响的观测值；λ和par0的参数优化。
8.在一些实施方式中，数据质量控制包括：当夜间摩擦风速低于临界摩擦风速时观测的nee数据剔除；剔除那些超出所设阈值，存在明显异常的 nee观测数据；剔除那些与降水同时段的nee观测数据；对nee观测数据进行统计进行3倍标准差的剔除筛选。
9.在一些实施方式中，λ和par0的参数优化包括：利用夜间的nee观测值通过蒙特卡
洛的方法得到呼吸参数α和β；利用α和β和站点温度观测值计算得到白天的生态系统呼吸re，由白天的nee减去re得到gee，；再利用vprm 中gee的计算公式以及对应的t
scale
、w
scale
、p
scale
、evi、par值反演拟合得到λ和par0。
10.在一些实施方式中，根据站点通量足迹模型剔除周边人为源对通量观测数据产生较大影响的观测值，包括：采用涡度相关co2通量的footprint 模式对co2通量观测数据进行筛选，剔除那些受人为源影响较为严重的co2通量观测数据。
11.在一些实施方式中，地基和多源卫星co2浓度数据的尺度匹配包括：卫星柱浓度尺度转换、多源数据融合及局地化技术。
12.在一些实施方式中，卫星柱浓度尺度转换包括：卫星柱浓度垂直尺度转换、多源卫星柱浓度的水平空间匹配和尺度转换。
13.在一些实施方式中，卫星柱浓度垂直尺度转换包括：把碳同化系统模拟的分层浓度插值到gosat/gosat-2、oco-2/oco-3或tansat卫星的分层高度，以碳卫星先验廓线、气压加权函数、平均核函数为基础，采用rodgers &connor的算法，计算与卫星柱浓度相匹配的模型模拟柱浓度。
14.在一些实施方式中，多源卫星柱浓度的水平空间匹配和尺度转换包括： oco-2/oco-3卫星一次打点8个，1秒打3次，对oco-2/oco-3在同1秒内的xco2观测数据求平均。
15.在一些实施方式中，局地化技术包括：分区；计算回归系数βi；计算权重α
min
；计算结合观测空间代表性的权重α
min，obs
；引入局地化函数后，执行同化分析。
16.在一些实施方式中，多源数据融合包括：进行分层浓度与柱浓度的转换；利用集合卡尔曼平滑enks方法对观测浓度进行统一同化。
17.此外，本发明还提供了一种同步反演高分辨率人为co2排放与自然co2通量的同化系统，所述系统包括：一个或多个处理器；存储装置，用于存储一个或多个程序；当所述一个或多个程序被所述一个或多个处理器执行，使得所述一个或多个处理器实现根据前文所述的同步反演高分辨率人为co2排放与自然co2通量的同化方法。
18.采用这样的设计后，本发明至少具有以下优点：
19.本发明使用wrf-ghg区域模式，选择华北平原为试验区，结合禹城地基站点观测数据和gosat与oco-2卫星柱浓度数据，运用pod4dvar的方法构建了区域高精度地基-多源卫星联合碳同化系统，实现了自然co2通量和人为co2排放的同步同化反演。
20.(1)在线耦合模型对vprm模型参数优化明显。在wrf-ghg模式框架下实现了生态诊断模型vprm与大气传输模型wrf的在线耦合，基于禹城通量观测数据优化vprm模型参数，接着从站点和区域尺度验证、评价模拟的生态系统co2交换(gee)和生态系统呼吸(re)。结果显示优化效果显著，说明参数优化之前模式对生态系统净co2通量(nee)存在明显低估问题。在区域尺度上把wrf-ghg碳同化系统参数优化后模拟的nee(5km分辨率) 与carbontracker-china的nee(1
°
x1
°
分辨率)反演值进行对比，结果表明两套数据季节变化基本一致，但是4月份wrf-ghg模型模拟的nee为碳汇，carbontracker-china反演的nee为弱的碳源，从nee通量大小的贡献量来看carbontracker-china的nee反演值，总体低于wrf-ghg区域碳同化系统的模拟值，主要原因是wrf-ghg同化系统模拟的nee精度更高，更能代表研究区域的co2通量特征，能捕捉到农作物更多的生态信息。
21.(2)wrf-ghg同化前后co2浓度模拟值结果验证。采用未参与同化的 gosat和oco-2
卫星柱浓度数据和地基co2浓度观测数据对同化前后的co2浓度模拟值进行了对比分析，同化前后co2浓度模拟值与gosat卫星柱浓度数据对比发现，在1月份和4月份相关性大约提高了17.7％，均方根误差 (rmse)平均降了66.7％；与oco-2卫星柱浓度观测信息对比，其系统模拟值比同化之前效果有很大提高，相关性大约提高了17％，rmse降低了大约 1ppm，平均偏差大约降了37.2％，误差的另一个测量指标ioa大约提高了 30％。同化后的站点模拟值与观测值之间的相关性提高了40％，同化后的平均偏差大约降了51.87％。
22.(3)wrf-ghg同化前后人为co2通量估算精度明显提高。在城市尺度上，以济宁、邯郸、淄博3个排放量大的城市为例进行了co2排放量验证统计，并与其他独立数据，即生态环境部规划院的中国城市2012年co2排放数据集进行对比分析，结果显示排放量基本一致，并发现其他基于传统方法的排放数据存在明显低估问题。在区域尺度上同化系统反演的人为碳通量同清华大学的meic通量产品进行对比，结果显示同化系统反演的人为碳通量更能体现季节的变化规律，在基于本发明技术计算反演值排放量上总体高于meic排放数据。
23.(4)基于本发明，实现了自然co2通量和人为co2排放的同步同化反演并优化，提高了传统人为co2排放清单空间分辨率粗放和严重时间滞后性问题，将成为正在实施的碳中和路径的不确定性评估的重要工具，为国家和省、市碳中和行动有效性评估提供科技支撑。
附图说明
24.上述仅是本发明技术方案的概述，为了能够更清楚了解本发明的技术手段，以下结合附图与具体实施方式对本发明作进一步的详细说明。
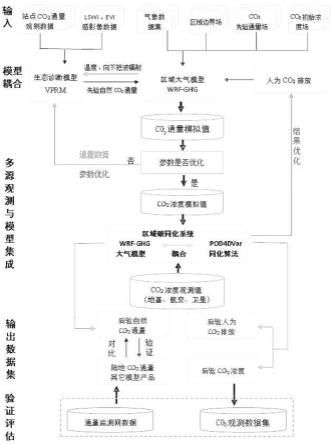
25.图1是同步同化人为排放与自然碳通量总技术路线图；
26.图2是耦合生态系统模型(vprm)-大气传输模型优化碳关键参数技术流程；
27.图3是耦合生态系统模型(vprm)关键参数优化技术流程图；
28.图4是co2柱浓度尺度转换技术示意图；
29.图5是wrf-ghg模式中新增模块的代码结构；
30.图6是区域碳同化系统运行流程图；
31.图7是示例嵌套模拟区域设置；
32.图8是禹城站周边区域地表覆被；
33.图9是同化系统运行周期示意图；
34.图10是不同集合下区域碳同化系统co2浓度模拟值与观测值对比；
35.图11是wrf默认modis地表覆被类型与lucc 2010年地表覆被类型分布图；
36.图12是wrf默认modis地表覆被数据与lucc 2010年地表覆被数据对比分析直方图；
37.图13是vprm模式优化输出流程图；
38.图14是春季gpp优化前后与观测值对比分析图；
39.图15是春季re优化前后与观测值对比分析图；
40.图16是春季nee优化前后与观测值对比分析图；
41.图17是夏季gpp优化前后与观测值对比分析图；
42.图18是夏季re优化前后与观测值对比分析图；
43.图19是夏季nee优化前后与观测值对比分析图；
44.图20是秋季gpp优化前后与观测值对比分析图；
45.图21是秋季re优化前后与观测值对比分析图；
46.图22是秋季nee优化前后与观测值对比分析图；
47.图23是冬季gpp优化前后与观测值对比分析图；
48.图24是冬季re优化前后与观测值对比分析图；
49.图25是冬季nee优化前后与观测值对比分析图；
50.图26是2016年四个月份(1、4、7和10月份)中午12:00区域尺度 (5km)平均光合作用强度；
51.图27是2016年四个月份(1、4、7和10月份)中午12:00区域尺度 (5km)平均呼吸作用强度；
52.图28是2016年四个月份(1、4、7和10月份)中午12:00区域尺度 (5km)平均地表温度；
53.图29是2016年四个月份(1、4、7和10月份)gpp、re和nee对研究区域贡献量的月均值；
54.图30是2016年四个月份(1、4、7和10月份)nee对研究区域的贡献量；
55.图31是同化系统反演的区域高分辨率(5km)人为源碳通量；
56.图32是城市尺度排放量对比分析；
57.图33是区域人为源碳通量统计分析。
具体实施方式
58.以下结合附图对本发明的优选实施例进行说明，应当理解，此处所描述的优选实施例仅用于说明和解释本发明，并不用于限定本发明。
59.技术方案的目标是发展同化算法，解决其无法区分人为co2排放和自然 co2通量的技术难题。核心技术包括如下两个部分：
60.(1)本发明通过正交4维变分(pod4dvar：pod-based four-dimensionalvariation data assimilation method)方法构造并求解人为co2排放源和 co2浓度的雅克比矩阵，实现目标函数最小化，采取多尺度交叉验证方法，实现co2通量和co2浓度双同化，并基于站点通量观测数据、采用蒙特卡洛参数优化方法对生态诊断模型参数进行优化。
61.(2)目前碳同化系统只是简单地把陆地生态模型当做一个先验通量的提供者，而没有实现大气传输模型与陆地生态系统模型的耦合，只对净碳通量(nee)进行同化反演，因而无法对两个碳通量分量生态系统初级生产力(gpp：gross primary productivity)和生态系统呼吸(re：ecosystemrespiration)进行直接反演，更无法对生态系统模型中关键参数(光合参数和呼吸参数)进行优化。该同化系统基于生态诊断模型和大气传输模型的在线耦合模式wrf-vprm(wrf-ghg模式中针对大气co2模块)实现自然碳通量(gee与re)和人为co2排放同步同化。
62.本发明总体技术方案如图1所示。
63.(1)解析遥感影像数据modis09a1数据，产生增强型植被指数(evi) 和地表水指数(lswi)数据集作为vprm输入数据；
64.(2)制备先验人为co2排放、生物质燃烧等数据，驱动wrf-ghg模型前向模拟co2浓度
场和自然co2通量场；
65.(3)基于所设置的模型模拟区域范围内的co2通量观测数据，对wrf-ghg 模型模拟的自然co2通量结果进行优化，并对嵌套于wrf-ghg模型中的自然生态co2诊断模型vprm模块进行参数优化，参数优化后的自然源co2通量误差很小并为人为co2排放的同化反演提供条件；
66.(4)基于尺度匹配后的地基和多源卫星co2浓度数据，采用pod4dvar 数据同化算法，实现地基-多源卫星联合同化，进而实现对人为co2排放的反演核算；
67.(5)生成区域高时空分辨率数据产品集(co2浓度场、自然co2通量场、人为co2碳排放场)；
68.(6)对(5)的4维数据集(三维立体空间+时间)进行准确性验证和模型鲁棒性验证；
69.(7)最后构建区域碳同化反演系统(rcas)，实现同步同化目标区域高分辨、高精度人为co2排放与自然co2通量。
70.所涉及的四个方面的核心方法及关键技术叙述如下。
71.3.2.1生态系统模型-大气传输模型耦合技术
72.基于碳卫星太阳诱导叶绿素荧光(sif)数据、13co2同位素观测数据以及生态系统碳通量观测数据，采用卡尔曼滤波(kalman filter)和马尔可夫链—蒙特卡罗(markov chain-monte carlo)同化方法，实现陆面生态模型与大气传输模型耦合，对陆面生态模型vprm中碳关键过程进行参数优化，实现生态系统co2通量分量(生态系统初级生产力gee和生态系统呼吸re) 及关键碳过程参数(最大光能利用率luemax、呼吸温度敏感参数(q10) 等)的同步优化。
73.陆面生态系统模型的优化是获取高精度先验自然碳通量的基础。利用站点co2通量及叶绿素荧光(sif)观测资料，结合野外调查材料，采用蒙特卡洛算法和资料同化技术(enkf)，实现对陆面生态模型vprm中碳关键过程进行参数的优化、对比和验证，实现陆面生态模型在站点尺度的优化 (图2)。
74.3.2.2陆面生态系统模型(vprm)参数优化方法
75.植被光合呼吸模型(vprm)是一种基于光能利用效率(lue)的陆地生态诊断模型，它是mahadevan在vpm模型的基础上发展而来，与vpm相比， vprm增加呼吸项(re)及其相关的呼吸参数α和β(在冰点温度时呼吸基础率)，以及用于反映光合有效辐射与光合作用关系的半饱和值参数par0。该研究以wrf模型耦合vprm生态诊断模型为基础，基于通量观测数据结合模拟自然碳通量值，反演光合、光合敏感参数，使用优化后的模型参数预测中国区域不同时空分辨率陆表碳通量分量的时空格局，基于多尺度地面观测与卫星产品，交差验证模拟结果，综合评价国内外现有碳同化系统和碳循环模型及参数，并为进一步改善wrf-vprm模拟区域大气co2浓度的时空变化打下坚实的基础。揭示自然与人为因素对大气co2浓度的相对历史贡献，分析其驱动机制与未来的变化趋势。
76.如图3所示，在vprm模型中，nee的计算主要包括两部分：其中一部分为总生态系统co2交换量gee，由光照驱动计算；另一部分为生态系统呼吸项re，由温度驱动计算。其具体表达式如下：
77.78.式中，λ(μmol co2m-2
s-1
/(μmol par m-2
s-1
))代表最大光能利用率(或最大光量子效率)，该参数在无水分压迫和温度适中的情况下对c3植物而言为1/6左(mahadevan等.，2008)，par0(μmol m-2
s-1
)代表光合作用达到半饱和值时对应的光合有效辐射。par(μmol m-2
s-1
)代表光合有效辐射，evi 为增强型植被指数，papar
pav
代表植被所吸收的光合有效辐射和光合辐射之间的比值(xiao等.，2004)。t
scale
、w
scale
和p
scale
代表对光合作用的影响函数，分别代表温度、水分胁迫和叶面性状，其计算公式如下：
[0079][0080][0081][0082]
式中，t代表气温，单位是(℃)，t
min
、t
max
和t
opt
分别代表光合作用所需要的最小、最大和最适温度。当空气温度低于t
min
，t
scale
不在采用公式 (4)计算，直接取值为0。lswi代表地表水分指数，lswi
max
是每个格网点生长季内最大的lswi值。植被处在不同的生长期阶段，其p
scale
的值不同，模式中对于常绿林p
scale
在全年中的值设为1.0。t
scale
、w
scale
和p
scale
3个函数值有一定的取值范围，其范围为0.0～1.0。公式(2.1)最后1项代表呼吸过程对nee的贡献。多数生态诊断模型把呼吸项看成是温度的指数函数，但是vprm模式将呼吸项简化为温度的线性函数。其中α(μmol m-2
s-1
/℃)、β(μmol m-2
s-1
/℃)可根据通量塔观测数据进行优化调整。
[0083]
为了使vprm能够更好的对研究区域进行生态碳通量的模拟，需要对 vprm参数进行优化。参照chinaflux通量数据后处理方法 (http：//www.chinaflux.org)以及falge等(2001)和zhang等(2006) 的方法对通量塔检测的nee数据进行一系列预处理，主要包括运用相关插值算法对缺失数据进行插补、坐标轴旋转、摩擦风速大小的质量控制、储存项计算和密度纠正计算等。参数优化时选择未插补和经过严格摩擦风速筛选的数据以避免数据处理不当引入误差。
[0084]
具体地，采用如下方案进行参数优化：
[0085]
(1)数据质量控制：当夜间摩擦风速低于临界摩擦风速时观测的nee 数据剔除；剔除那些超出所设阈值，存在明显异常的nee观测数据；剔除那些与降水同时段的nee观测数据；对nee观测数据进行统计进行3倍标准差的剔除筛选。
[0086]
(2)根据站点通量足迹模型(footprrint模式)(chen等.，2009) 剔除周边人为源对通量观测数据产生较大影响的观测值。
[0087]
(3)参数优化：利用夜间的nee观测值通过蒙特卡洛的方法得到呼吸参数α和β。利用α和β和站点温度观测值计算得到白天的生态系统呼吸re，由白天的nee减去re得到gee，本文提到的gee数值大小和gpp一致，只是符号相反，下同。再利用vprm中gee的计算公式以及对应的t
scale
、w
scale
、p
scale
、 evi、par值反演拟合得到λ和par0[0088]
以华北平原应用案例为例，参与参数优化的禹城站通量观测数据需要严格的质量控制，除了上面提到的常规的质量控制以外，本研究采用涡度相关co2通量的footprint模式对co2通量观测数据进行筛选，剔除那些受人为源影响较为严重的co2通量观测数据。
[0089]
3.2.3卫星柱浓度尺度转换、多源数据融合及局地化技术
[0090]
(1)co2浓度观测数据
[0091]
项目申请依托中国精度co2浓度全球大气本底站、我国区域背景站、校验站数据，收集整理的全球站点(https://gml.noaa.gov/ccgg/obspack/) 和多源卫星观测数据分别来自gosat(下载路径：https://disc.gsfc.nasa.gov/datasets？keywords＝gosat&page＝1，acos-gosat v9r)、gosat-2(下载路径:https://prdct.gosat-2.nies.go.jp/aboutdata/howtoaccessdata.html.en#01_howto)、oco-2(下载路径:https://disc.gsfc.nasa.gov /oco-2，oco2_l2_lite_fp v10r)、oco-3(下载路径:https://disc.gsfc. nasa.gov/oco-3，oco3_l2_lite_fp earlyr)和tansat(下载路径:http:/ /data.nsmc.org.cn/portalsite/data/satellite.aspx)。利用多源卫星观测开展碳源汇估算以及大气co2反演法优化研究时，要求碳卫星xco2测量精度达到1ppm(～0.3％)。因此，我们从gosat、oco-2及tansat卫星观测数据中过滤出误差《1ppm的数据进入碳同化反演系统。
[0092]
(2)卫星柱浓度垂直尺度转换
[0093]
在将卫星数据引入碳同化系统之前，首先要对卫星柱浓度数据与大气传输模型模拟浓度间的尺度进行转化，实现观测浓度与模拟浓度间的尺度匹配。目前已有多种方法用于实现模拟浓度的尺度转换，按照gosat/gosat
ꢀ‑
2、oco-2/oco-3、tansat卫星参数及本项目的尺度要求，选择卫星核函数尺度转化法(图4)，实现模拟浓度与卫星柱浓度的尺度匹配。尺度转换过程如下：把碳同化系统模拟的分层浓度插值到gosat/gosat-2、oco-2/oco-3 或tansat卫星的分层高度，以碳卫星先验廓线、气压加权函数、平均核函数为基础，采用rodgers&connor的算法(rodgers cd,connor bj(2003) intercomparison of remote sounding instruments.j geophys res. doi:10.1029/2002jd002299)，计算与卫星柱浓度相匹配的模型模拟柱浓度：
[0094][0095]
其中，是转化后的模拟柱浓度；h
t
是卫星(gosat/gosat-2、 oco-2/oco-3、tansat)提供的气压加权函数；xa是卫星(gosat/gosat-2、 oco-2/oco-3、tansat)的先验廓线；a分别是gosat/gosat-2、oco-2/oco-3、 tansat的平均核函数；xh是大气传输模型在卫星分层高度插值获取到的模拟浓度。对于卫星本身不能提供核函数、先验廓线等信息的，我们将借助其它方法(如tccon柱浓度转换法)或其它模型参数(如rcas同化系统提供的先验廓线信息)按公式(2.1)进行转化。
[0096]
(3)多源卫星柱浓度的水平空间匹配和尺度转换
[0097]
多源碳卫星的空间分辨率各异，gosat、gosat-2、oco-2/oco-3和tansat 空间分辨率分别为10.5km
×
10.5km、9.7km
×
9.7km、1.29km
×
2.25 km和2km
×
2km，需要根据模式输出格网的大小进行空间分辨率统一化处理。根据模式分辨率选择与gosat和gosat-2空间分辨率接近的10km
×ꢀ
10km作为多源碳卫星空间匹配标准。oco-2/oco-3和tansat分辨率远大于10km
×
10km，需进行空间尺度匹配，其中，oco-2/oco-3卫星一次打点8个(1.29km
×
8个≈10km)，1秒打3次(24个点,2.25km
×ꢀ
3次≈7km)，我们对oco-2/oco-3在同1秒内(《＝24个点，注意部分点会由于气溶胶污染(一般光学厚度aod》0.3时)被过滤掉)的xco2观测数据求平均，以尽量使得卫星观测点向空间匹配标准靠近。对于tansat，我们采取类似于oco-2/
oco-3的空间处理方式。综合水平空间匹配和垂直尺度转换的模拟浓度计算公式如下：
[0098][0099]
其中，i代表的是第i个卫星观测，n为1秒内获取的卫星观测总数(对于oco-2/oco-3，在假设没有卫星点被过滤掉的情况下，其n＝24)。式中其它参数说明请参考公式(1)。
[0100]
(4)多源观测的自适应局地化方案
[0101]
由于站点、卫星等多源观测数据的空间分辨率及时空代表性不相同，其观测影响周围状态量的空间范围也不相同。本发明技术结合观测数据类型、格网距离信息采用分级集合滤波技术来研制考虑多源观测数据同化影响范围的局地化方案。局地化技术及过程如下：
[0102]
1)分区：为减小计算量、提高计算效率，将整个模拟区域均匀划分为 m个小区(每个方块中包含有n个成员，所以集合成员总数为m
×
n)，每个小区的中心点选定为“局地化中心”。
[0103]
2)计算回归系数βi：对模拟区分区后，开始计算各小区的回归系数。任一个观测对小区i的回归系数βi计算公式如下：
[0104][0105]
式中分子σ
x，y
表示由第i组集合计算得到的x和y先验样本协方差，分母σ
y，y
表示观测的先验方差。分子σ
x，y
和分母σ
y，y
对应为数据同化中的 ph
t
和hph
t
(h为观测算子，p为背景误差协方差矩阵，上标t表示转置，x 表示状态变量，y表示观测)。
[0106]
3)计算权重α
min
：假设忽略其它的误差源，回归系数βi的真值应从一个回归系数样本的相同分布中随机获得。样本的不确定性反映了计算得到增量的不确定性。因此，我们定义回归置信因子α，使得增量值和利用准确计算得到的增量值之间的均方根误差数学期望最小化：
[0107]
即最小化公式：
[0108][0109]
等价于：
[0110][0111]
对α求导并令其为0：
[0112][0113]
最终求解得到置信因子α
min
，即作为观测对状态量的影响权重系数：
[0114][0115]
4)计算结合观测空间代表性的权重α
min，obs
：根据空间代表性，对站点、卫星观测数据进行空间代表性分级，并给定代表性系数ξ。定义站点观测代表性系数ξ为1，gosat/
gosat-2代表性系数ξ为0.7， oco-2/oco-3/tansat的代表性系数ξ为0.5。更新后的权重α
min，obs
如下：
[0116]
α
min，obs
＝α
min
×
ξ
ꢀꢀꢀ
(3.8)
[0117]
5)在同化系统中的技术实现方法：α
min，ob
s为观测对模式状态量的局地化权重系数。引入局地化函数后，同化分析方程变为：
[0118][0119]
该方法按照观测与背景场模式状态量间误差的相关性给予不同等级的局地化影响权重，因此，将这种分级集合滤波同化技术是高效的自适应局地化方案。
[0120]
(5)卫星-地基co2数据融合技术
[0121]
卫星监测资料具有覆盖面广、时空分辨率高的特点。它的引进改善现有的大气co2反演模型观测数据不足的现状。卫星-地基co2数据联合同化方法的关键技术是如何把模拟的co2浓度转化为与卫星浓度同一个尺度的柱平均浓度，以方便模型进行对比、分析及数据同化。我们利用公式(3.10) (rodgers et al.(2003)进行分层浓度与柱浓度的转换。
[0122][0123]
其中，是我们转化后的模拟平均柱浓度；h
t
是卫星提供的气压加权函数；xa是卫星提供的先验廓线；a是卫星提供的平均核函数；xh是大气传输模型在与卫星相对应的分层高度插值获取到的模型浓度。
[0124]
将分层模拟浓度转化为柱浓度后，利用集合卡尔曼平滑enks方法对观测浓度(包含地基观测和卫星观测)进行统一同化(图4)。
[0125]
整个技术路线分2步走：
[0126]
(1)根据观测点(x,y,t,z)的坐标(x,y)、时间(t)、高度(z)信息提取相应的模拟浓度，首先判断当前的观测数据类型：如果是站点观测点，系统直接采样提取相应浓度数据；如果不是站点数据，则要根据公式 (3.10)对大气传输模型模拟的分层浓度进行转化，计算出与观测数据相对应的柱平均浓度。
[0127]
(2)再通过最小化观测与模拟浓度间的差值来同化co2的浓度与通量。
[0128]
3.3.4pod4dvar高效co2同化方法
[0129]
本研究将本征正交分解法(pod，proper orthogonal decomposition) 应用到四维变分同化(4dvar，four-dimensional variational dataassimilation)算法中(tian等.，2009,2011)，结合wrf-ghg模型，构建了基于本征正交分解的四维变分同化反演模型，在很大程度上降低了同化反演所需计算机资源，提高了运算效率和估算精度。该模型考虑了co2滞后特征，可同化地基、卫星等多源co2浓度观测数据，反演得到全球和区域等不同尺度的碳通量。
[0130]
pod4dvar是一种基于本征正交分解的显式四维变分方法，它运用蒙特卡洛的方法生成类似于集合卡尔曼滤波方法(enkf)的四维样本集合。由于pod正交基具有最小二乘意义上的最优性，将pod方法应用于四维空间的预报集合提取正交基，它可以捕获预报集合的更多能量，更好的表征四维变量的空间结构和时间演变特征。该方法无需积分伴随模式，在运行和维护上都较为简便。
[0131]
由于传统的4dvar数据同化方法需要求取切线和伴随线性算子，然而对于非线性
的模型算子求取切线和伴随算子是非常困难的。pod4dvar能够把隐式的优化问题显式化，用一组基向量捕捉数据的时空演变特征。这种方法不仅简化了数据同化的过程，而且保留了传统4dvar的两大优势：(1) 该方法可以提供时间平滑性约束(2)在一个同化窗口中可以把多个时次的观测数据引入。尤其当初始场误差和预报模型不确定性明显的模式运用 pod4dvar方法进行数据同化，其同化效果尤为明显。
[0132]
传统的4dvar，通过模型的模拟值与观测值之间的差异构造代价函数 (公式4.1)，对代价函数求导获取后验通量
[0133][0134][0135]
其中t代表矩阵转置，b为背景场co2人为碳通量值，k代表co2浓度观测时间序列，hk代表观测算子，矩阵b和r分别代表通量背景误差和浓度观测误差协方差。代表同化窗口初始时刻的控制变量(即先验通量)。在代价函数中通过公式(4.2)与联系在一起。很显然代价函数关于的梯度值很难获取，然而pod4dvar方法大大简化了其计算过程。在pod4dvar 同化算法中，假设在同化窗口(0，t)中有s个时间序列，用蒙特卡洛方法在t＝t0时刻对初始人为碳通量数据添加扰动，生成n个初始场集合 n＝1,2,
…
,n。通过公式(4.2)获得所用同化窗口内的，所有集合的状态变量：
[0136][0137]
当扰动样本足够大时，样本集合可以基本表征状态变量的时空特征，所有的状态变量的扰动信息能被扩展到一个有限维的向量空间同样最后的目标分析资料在整个同化窗口内能被表示为：
[0138][0139]
当集合数n增加到一定数量，分析状态向量能够被集合空间所表示，假设ω的基向量线性空间用表示,分析状态向量能够表达为基向量的线性组合：
[0140][0141]
用公式(4.4)和(4.5)重写公式(4.1)，由β＝(β1...βk)
t
替换，因此状态变量在代价函数中被显示化，梯度计算在很大程度上被简化。切线模型和伴随模型不再需要。最小代价函数公式(4.1)用变量β显式处理之后，其能用一般的优化算法计算。但是与enkf不同的是，此算法在每一次的同化循环中，初始状态变量在初始时刻都应该添加扰动，并且最后的优化结果只能获得一组。接下来的重点就是怎样获取合适的基向量。
[0142]
n个集合状态向量的平均值表示如下：
[0143][0144]
根据构建一个新的偏差向量集合：
[0145][0146]
其构建的矩阵a(m
×
n)，m＝mg×mv
×
s，其中mg，mv分别表示模式空间格点的数目和模型变量的数目(这里仅代表人为碳通量)。为了计算本征正交分解(pod)的数目，需要解决特征值问题：
[0147]
(aa
t
)m×mv＝λv
…
(4.8)
[0148]
在实际中m≥n，因此为了解决高效方便的求解问题，将其转化为n
×
n 的特征值问题，转化方式如下：
[0149]at
av＝λv
[0150]
aa
t
av＝aλv
[0151]
aa
t
(av)＝λ(av)
…
(4.9)
[0152]
此时转化为求取n
×
n的特征值问题：
[0153]
tvk＝λ
kvk
，k＝1，...，n
…
(4.10)
[0154]
其中t＝(a
t
a)n×n，vk是特征向量v的第k列，λk是特征值λ第k行。由于t为对称半正定的，因此得到一组降序排列的特征值λ1≥λ2≥
…
λn≥0。非零特征值λk(1≤k≤n)被挑选用来标准正交化，并且pod模式被给出，通过
[0155]
在四维空间中可以用pod重写，其表示方式为：
[0156][0157]
其中p为pod模式的数目，其大小的确定按照下面的公式：
[0158][0159]
其中，0＜γ＜1表示由降维空间d
p
＝span{φ1，...φ
p
}所捕获的总能量的百分数。为了捕获pod基的大部分能量，允许γ在1附近取值。根据公式(4.4) 和(4.9)重构代价函数(4.1)，控制变量β＝(β1，β2，...，β
p
)
t
代替初始时刻的状态变量如此控制变量在代价函数中被显式处理，在求取代价函数最小值的过程中，切线算子和伴随模式不在需要。求取代价函数的最小值问题，转化成用一般的优化算法求取β＝(β1，β2，...，β
p
)
t
的问题。然而β的求取仍然需要迭代过程，依旧有很高的计算量。此问题被解决按照如下流程：
[0160]
构建pod模式矩阵：
[0161]
φ＝(φ1，φ2，...，φ
p
)...(4.13)
[0162]
其中φj＝(φj(t0)，φj(t1)，...，φj(t
s-1
))
t
，j＝1，2，...，p转化公式(2.15)为：
[0163]
φ＝(φ1，φ2，...，φ
s-1
)...(4.14)
[0164]
其中φk＝(φ1(tk)，φ2(tk)，...，φ
p
(tk))，公式(2.13)被重写如下：
[0165][0166]
其中β＝(β1，β2，...，β
p
)
t
。用公式(2.17)重写代价函数：
[0167][0168][0169]
其中，hj是切线观测算子，co2浓度观测向量其中mj是观测向量的个数，可用通过扰动的方式使某一时刻的观测值产生n个集合，其表示为：
[0170][0171]
式中，n个集合的扰动平均值为0，用矩阵表示为： ej＝(ε1，ε2，...，εn),观察误差矩阵能够按照公式(4.18)进行评估。
[0172][0173]
背景误差协方差b的构造方式类似于观测误差协方差r的构造方式。
[0174]
由于是对称矩阵，代价函数的梯度通过简单的计算就很容易获得，
[0175][0176]
为了求取代价函数最小值，需要即：
[0177][0178]
经过以上的一系列转化之后，公式(4.20)可以不需要迭代过程直接计算获取，这就大大简化了计算量，提高了同化反演效率。
[0179]
以上所述，仅是本发明的较佳实施例而已，并非对本发明作任何形式上的限制，本领域技术人员利用上述揭示的技术内容做出些许简单修改、等同变化或修饰，均落在本发明的保护范围内。