一种考虑不确定性的感应电机降耗优化方法

1.本发明涉及电机技术领域，具体涉及一种考虑不确定性的感应电机降耗优化方法。
技术背景
2.电机作为电动汽车(ev)的动力源，其设计优化已成为研究热点。它是将电能转化为机械能的关键部件，其选择对电动汽车的性能起着重要作用。一般来说，电机效率的提高为节能提供了更大的可能性，它与结构设计和起动控制策略密切相关，可以通过确定性优化来增强。然而，仅仅通过确定性优化并不能保证性能可靠性，因为设计和制造过程中存在各种不确定性，可能导致实际性能和预期性能之间存在偏差。性能偏差不仅体现在与初始设计相比性能下降，还可能导致约束条件失效，进而导致起动能力下降或热失控。因此，通过探讨电机制造过程的不确定性，提高电机性能。


技术实现要素：

3.本发明的目的是减少制造公差对电机起动性能的影响。在满足电机起动转矩和启动电流的条件下，基于可靠性的设计方法，使用感应电机的自适应加权响应面法对转子的槽尺寸进行设计，建立了一种考虑不确定性的感应电机降耗优化方法。
4.为实现本发明目的而采用的技术方案是这样的，即一种考虑不确定性的感应电机降耗优化方法，包括以下步骤：
5.步骤1：从结构方面分析影响感应电机性能的因素，建立以电机转子槽尺寸为变量的电机总损耗、起动转矩和起动电流的代理模型；
6.步骤2：以电机总损耗为目标，电机转子的槽尺寸为随机优化变量，起动转矩和起动电流值为可靠性约束，基于径向基函数神经网络建立考虑不确定性的感应电机降耗优化模型；
7.步骤3：采用序列二次规划算法求解优化模型，优化过程中采用自适应加权响应面法近似极限状态函数，并结合蒙特卡罗模拟方法进行可靠性分析。
8.2.根据权利要求1所述的一种考虑不确定性的感应电机降耗优化方法，步骤1中，建立代理模型的过程为：
9.(1)通过从结构方面分析影响性能的因素，选取槽口高h
s0
、槽高h
s2
、上槽宽b
s1
、下槽宽b
s2
为设计变量，总损耗、起动转矩和起动电流为研究目标；
10.(2)采用拉丁超立方抽样在设计空间采样，获得电机的总损耗、起动转矩和起动电流参数值；
11.(3)基于径向基函数神经网络建立总损耗、起动转矩和起动电流的代理模型；
12.根据权利要求1所述的一种考虑不确定性的感应电机降耗优化方法，步骤2中，建立的优化模型为：
13.(1)设计变量：
14.转子槽尺寸：槽口高h
s0
、槽高h
s2
、上槽宽b
s1
、下槽宽b
s2
；
15.(2)目标函数：
16.min p
loss
(h
s0
,h
s2
,b
s1
,b
s2
)
17.其中，p
loss
为总损耗；
18.(3)约束条件：
19.起动转矩和起动电流作为可靠性约束，对转子的槽尺寸进行工艺约束；
[0020][0021]
其中，p表示概率，t
st
为启动转矩，i
st
表示启动电流，r1为起动转矩可靠性，r2为启动电流可靠性，受不确定性影响的变量实际值，服从分布，h
s0l
和h
s0u
为h
s0
的最小值和最大值，
[0022]
受不确定性影响的变量实际值，服从分布b
s1l
和b
s1u
为b
s1
的最小值和最大值，受不确定性影响的变量实际值，服从分布，h
s2l
和h
s2u
为h
s2
的最小值和最大值，受不确定性影响的变量实际值，服从分布，b
s2l
和b
s2u
为b
s2
的最小值和最大值；
[0023]
根据权利要求1所述的一种考虑不确定性的感应电机降耗优化方法，步骤3中，优化模型进行求解的过程为：
[0024]
(1)本发明采用自适应加权响应面法逼近极限状态函数：
[0025]
1)运用自适应加权响应面法将极限状态函数近似为：
[0026][0027]
其中，是响应面函数值，xi是第i个随机设计变量，β0是常数项，βi是线性项的系数，β
ij
交叉项的系数，n是随机变量的个数；
[0028]
2)获取权重系数：
[0029]
对离极限状态函数更近的实验点赋予更高的权重：
[0030]ybest
＝min|g(x
l
)|
[0031]
d(x
l
)＝g(x
l
)-y
best l＝1,2
…
,l
[0032][0033]
其中，y
best
定义为离极限状态函数最近点的距离，l代表每次迭代的实验点数，g(x)表示功能函数，d(x
l
)是其余实验点到最近实验点的距离，w
l
为权重系数；
[0034]
通过最小二乘法回归方法获得到权重矩阵：
[0035][0036]
系数矩阵可表示为：
[0037]
β＝[x
t
w(x)x]-1
x
t
w(x)y
[0038]
其中，x为随机变量的n维向量，w(x)是权重的对角矩阵；
[0039]
3)更新实验设计的中心点，在新实验设计中心采用饱和设计采样:
[0040][0041]
其中，xm新中心点，xd是当前设计点，是变量均值；
[0042]
(2)采用蒙特卡罗模拟方法进行可靠性分析，考虑系统的不确定性时会产生超出可行域的扰动设计因此，第j个约束gj(x)的可靠度表示为：
[0043][0044][0045]
其中，n是蒙特卡罗模拟中的测试样本数量，是指标函数，n足够大，以保证可靠性计算的准确性；
[0046]
(3)采用序列二次规划算法求解优化模型。
[0047]
与现有感应电机设计相比，本发明的有益效果是：
[0048]
本发明提出了一种考虑不确定性的感应电机降耗优化模型，建立了感应电机总损耗、起动转矩、起动电流的代理模型；以转子的槽尺寸为优化变量，以转子槽尺寸作为尺寸约束，同时以起动转矩和起动电流值作为可靠性约束，以最小的电机总损耗为目标的优化模型，有利于实现感应电机降耗可靠性优化设计；利用二次规划来计算梯度，蒙特卡罗模拟和自适应加权响应面法进行可靠性分析；最终优化结果表明，本发明所提出的设计优化方法能有效减小感应电机的总损耗，提高起动转矩和起动电流的可靠性，验证了优化结果的可靠性。本发明针对感应电机转子槽尺寸进行可靠性优化设计，对于感应电机的设计方案具有积极作用，从设计阶段考虑到转子的制造公差，能够进一步降低机床的总损耗，提高电机的可靠性。
附图说明
[0049]
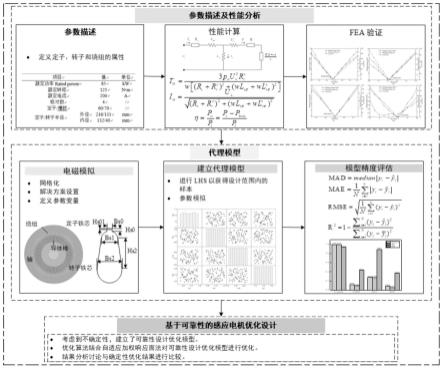
图1考虑不确定性的感应电机降耗优化流程
[0050]
图2感应电机模型(a)物理模型(b)感应电机的配置和转子槽的初始形状
[0051]
图3感应电机单项等效电路
[0052]
图4不同槽尺寸的性能(a)h
s0
(b)h
s2
(c)b
s1
(d)b
s2
[0053]
图5结合awrsm的可靠性设计优化算法流程图
具体实施方式
[0054]
下面结合附图和实施例对本发明作进一步说明，但不应该理解为本发明上述主题范围仅限于下述实施例。在不脱离本发明上述技术思想的情况下，根据本领域普通技术知识和惯用手段，做出各种替换和变更，均应包括在本发明的保护范围内。
[0055]
本实施例以某型号感应电机为研究对象，进行感应电机降耗可靠性设计优化。
[0056]
物理模型如图2(a)所示，其规格如表1所示。从技术上讲，导体棒的尺寸小于转子槽的尺寸。在发明中，为了方便进行有限元模拟，槽和导体条的尺寸被认为是相同的。转子配置和转子槽的初始形状如图2(b)所示。
[0057]
表1感应电机参数
[0058][0059]
对选取的槽尺寸b
s1
、h
s2
、b
s1
、b
s2
自变量，将感应电机等效为如图3所示单相等效电路is和分别是流过定子、转子绕组的电流，rs是定子电阻，是转子计算的定子电阻，l
sσ
是定子漏电感，是转子计算的定子漏电感，s是滑差率。
[0060]
转子导条截面积ar以被认为是槽尺寸的函数，表示为
[0061]ar
＝f(h
s0
,h
s2
,b
s1
,b
s2
)
[0062]
结合以下各式
[0063][0064]
计算转子电阻受槽尺寸的影响为
[0065][0066]
式中，是转子相对于定子侧的趋肤效应系数，与电机的配置参数有关。如果不考虑趋肤效应，它是恒定的。转子电阻rr由转子棒r
bar
和端环r
end
的电阻组成。r
end
被视为常数。ρ是电阻率，lb是导体棒的长度，ar是转子导条截面积。b
s1
、h
s2
、b
s1
、b
s2
为转子的槽尺寸。
[0067]
结合的定义和λu的定义
[0068][0069]
式中，l
rσ
为转子漏电感，μ0为真空磁导率，λu和λ
end
为转子槽和鼠笼端环的磁导系数。磁导因子λu与槽类型和相应尺寸紧密相关，而如果槽尺寸发生变化，则λ
end
是恒定的。
[0070]
计算转子电阻受槽尺寸的影响为
[0071][0072]
基于上述的转子电阻计算，结合感应电机的电磁转矩解析式
[0073][0074]
计算起动转矩t
st
和起动电流i
st
受槽尺寸的影响为
[0075][0076][0077]
根据电机的效率和总损耗表达式
[0078][0079]
p
loss
＝p
iron
+p
scu
+p
rcu
+p
me
+p
stray
[0080]
可以看出总损耗p
loss
会受到槽尺寸变化的影响因此进一步对总损耗、起动转矩和起动电流进行电磁有限元分析，结果如图4所示。当槽尺寸在初始值波动时，存在一定的性能偏差。对于b
s1
，在0.6mm的偏差下，总损耗p
loss
偏差高达近200w，起动电流偏差高达60a，起动转矩偏差高达10n
·
m，对于电机的稳定运行和安全性有相当大的波动。
[0081]
本发明采用代理模型的方法构建转子槽尺寸和之间的总损耗、起动转矩和起动电流的隐含关系，选择拉丁超立方方法(lhs)进行抽样。
[0082]
采用径向基函数(rbf)神经网络建立代理模型，为了验证rbf的有效性，将其与克里金法(kriging)和响应面法(rsm)法进行对比，采用中值绝对偏差(mad)、最大绝对误差(mae)、均方根误差(rmse)和r-square验证模型的精度，各精度数据如表2所示，可知三种性能的rbf预测值与观测值相比具有更精确的逼近效果。
[0083]
表2.代理模型评价指标值
[0084][0085]
在此代理模型的基础上，为了管理由感应电机转子槽制造公差导致的不确定性，建立了可靠性设计优化模型。将自适应加权响应面法(awrsm)与蒙特卡罗模拟(mcs)方法结合用于可靠性优化设计的可靠性计算中。
[0086]
可靠性优化设计模型通常表述为：
[0087]
minf(x)
[0088][0089]
四个槽尺寸b
s1
、h
s2
、b
s1
、b
s2
的范围为尺寸约束，在制造过程中，槽口尺寸通常会偏离设计值，实际值在标称值附近变化。设计变量是独立的随机变量，服从正态分布x～n(u,σ2)。公差通常接近标称尺寸值的
±
2％，因此，优化中标准差σ的数值设为0.02u；起动电流、启动转矩为可靠性约束；总损耗p
loss
作为优化目标，可靠性设计优化数学模型可用下式表示：
[0090]
min p
loss
(h
s0
,h
s2
,b
s1
,b
s2
)
[0091][0092]
其中r1和r2是目标可靠性，设置为0.9505，是受不确定性影响的变量实际值。随机变量的性质如表3所示。
[0093]
表3.随机设计变量的分布和界限
[0094][0095]
为了求解已建立的优化模型，使用顺序二次规划(sqp)来计算梯度。如图5所示，在
优化过程中，采用awrsm自适应逼近极限状态函数，采用mcs方法进行可靠性分析。
[0096]
对比确定化设计和可靠性设计，两种设计优化结果和初始值如表4所示，可靠性设计的优化设计可以满足可靠性要求，而确定性设计对于可靠性值分别为0.479和0.503的两个约束条件失败。约束失效意味着受制造过程不确定性的影响，启动转矩可能小于156.25n
·
m的概率为52.1％，启动电流大于1150a的概率为49.7％。两个优化模型的结果在目标值上都比初始计划的效果更好，其总损耗分别减少了6.74w和80.8w。
[0097]
表4感应电机的优化结果
[0098][0099]
将优化结果进行重构并将设计变量带入电磁有限元分析(fea)仿真模块来验证。总损耗的优化值与验证值对比如表5所示。将可靠性设计的优化设计变量带入仿真后的总损耗p
loss
为5990.1w，与优化值相比误差仅为0.0176％。同样，将确定性优化的优化设计变量带入仿真后的总损耗p
loss
为5918.9w，与优化值相比误差仅为0.0304％。这说明得到的最优结果足够准确。