一种基于绝对节点坐标法的聚酯缆系泊参数优化方法

1.本发明涉及海洋技术中聚酯缆系泊优化设计领域，尤其涉及一种基于绝对节点坐标法的聚酯缆系泊参数优化方法。


背景技术：

2.目前，在深海锚泊系统的合成纤维材料的应用和尝试较多，这些合成材料的力学性能与锚链的差别在于其表现出的粘弹性、粘塑性等材料非线性问题；同时，对于不同材料的纤维缆，还表现出了不同的蠕变、迟滞、动刚度等特性。在众多不同材料的合成纤维缆中，聚酯缆因其良好的特性成为备受青睐的深水系缆。聚酯缆的优点可以总结为以下几个方面：(1)重量轻：水中接近自浮；因质量轻，可采用张紧式系泊系统，相比悬链式系泊方式，可减少约40％的系泊半径，从而降低采办费用；(2)价格低：相同破断强度的聚酯缆采办成本远低于钢缆；(3)抗海水腐蚀：在海水中不发生腐蚀，不需要腐蚀余量或阳极保护；(4)抗疲劳性好：实验证明其疲劳性能要远好于钢缆和锚链；(5)强度高：强度/质量比高。但聚酯缆也有不抗磨、易受损、易蠕变、刚度非线性问题显著等缺点。
3.由于聚酯缆非线性问题的复杂性，许多缆索动力响应分析方法己不再适用。


技术实现要素：

4.本发明要解决的技术问题是如何提供一种基于绝对节点坐标法的聚酯缆系泊参数优化方法，能够对聚酯缆进行动力响应分析。
5.为了解决上述技术问题，本发明提供了一种基于绝对节点坐标法的聚酯缆系泊参数优化方法，包括以下步骤：。
6.本发明的技术效果在于：本发明通过多目标函数布谷鸟算法程序与基于ancf聚酯缆系泊计算程序相结合，能够考虑聚酯缆材料粘弹性，且提高了聚酯缆系泊优化设计计算的速度和准确度，结合帕累托解集取得最优解，使最优解的适应度更优。本发明可适用于各类型系泊系统优化设计，且优化效率高，精度好，操作简单，可根据不同需求更改目标函数的定义。
附图说明
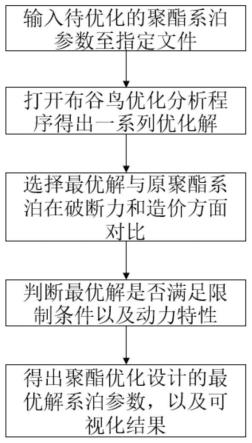
7.图1为聚酯优化设计流程图。
8.图2为布谷鸟优化算法的基本步骤流程图。
9.图3为帕累托前沿生成图。
10.图4为静力特性比较图。
11.图5为动力特性比较图。
12.图6为输出结果文件图。
具体实施方式
13.下面结合附图和具体实施例对本发明作进一步说明，以使本领域的技术人员可以更好的理解本发明并能予以实施，但所举实施例不作为对本发明的限定。
14.本发明实施例提供了一种基于绝对节点坐标法的聚酯缆系泊参数优化方法，结合附图1-6所示：
15.一种基于绝对节点坐标法的聚酯缆系泊参数优化方法，包括以下步骤：
16.s1、根据聚酯缆系泊系统的工作特点，确定待优化的系泊参数和设计参数的限制条件；
17.s2、采用布谷鸟优化理论计算得出一系列的优化解，选出最优解；
18.s3、将最优解与原聚酯系泊在力学性能和成本做对比；
19.s4、判断最优解是否满足限制条件和动力特性；
20.s5、得出聚酯优化设计的最优解系泊参数和可视化结果。
21.步骤s2的具体步骤包括：
22.s21、根据系泊参数的取值范围，设置目标函数
[0023][0024][0025][0026]
其中，fit(1)、fit(2)、fit(3)分别代表优化相关的目标函数，fit(1)代表聚酯段处张力与该段上破断力相关的目标函数，fit(2)代表单根系泊缆优化前后的总体造价相关的目标函数，fit(3)代表单根系泊缆优化前后张力相关的目标函数；ti代表聚酯缆段某点处的张力，fbi代表某点出的破断力，fbj＝170466*d2kn；cj代表直到j点处时的系泊缆总体价格，c为原来系泊参数的总价格；i和j分别代表聚酯缆段和总体系泊缆的节点；
[0027]
计算水平力、竖直力、系泊缆张力采用集中质量法，将系泊线的每个点看作节点，通常，除两端点外，节点上的集中质量取为相邻两段系泊线单元质量之和的一半，考虑第j个点在任意方向的运动，设j点x和z方向的分量为由引起的节点的张力为f
nxj
，设其在x、z方向的分力分别为则有以下的关系式：
[0028][0029][0030][0031]
[0032]
式中，a
nj
为j点法向附加质量；c
hn
为j点的法向附加质量系数；dc为等效截面直径；为线段的长度；是第(j-1)与第j个集中质量处系泊线倾角的平均值，即ρ为流体密度。根据以上推导，同理可得由引起的法向张力f
nzj
在x、z方向的分力分别为
[0033]
s22、产生随机初始化种群以及计算响应的初始适应度；
[0034]
s23、扩大种群范围，循环次数为最大迭代次数；
[0035]
s24、种群位置更新，并扩展适应度函数范围；
[0036]
s25、寻找新的解，并继续筛选出非支配解；
[0037]
s26、判断非支配解数量是否高于种群数量，若高于，则继续循环；若低于，则结束循环并得出帕累托最优解集。
[0038]
在步骤s1中，待优化参数包括以下五部分：
[0039]
(1)求解控制参数，迭代步数，结果输出间隔；
[0040]
(2)系泊各段的直径、干重、拉伸刚度、弯曲刚度、划分单元数；
[0041]
(3)计算工况参数，包括水深、水密度、波高、波浪周期、流速、流向；
[0042]
(4)总体的长度以及单元数；
[0043]
(5)单元的属性，包括聚酯、钢缆以及铁链。
[0044]
在步骤s2中，从帕累托最优解集中选择对应适应度值最小的一组参数，即为最优解。
[0045]
本发明是在考虑聚酯缆材料非线性的前提下优化系泊设计参数，满足聚酯缆破断力设计合理性以及整体系泊造价最低。
[0046]
选择多目标函数布谷鸟优化算法来提高待优化计算的收敛速度，保证优化结果的精度。
[0047]
首先根据聚酯缆系泊系统的工作特点，确定待优化的系泊参数、设计参数的限制条件以及目标函数；其次，结合基于ancf理论的系泊分析程序，确定非支配解种群数量，并获取适应度函数取值范围，对聚酯缆系泊进行优化设计，得出最优结果；最后，通过程序中的帕累托前沿确定系泊参数的最优解，并将优化后的系泊系统与原系统进行静动力计算结果对比分析，确保优化设计结果的准确性。
[0048]
布谷鸟优化算法是基于生物进化过程而总结出的方法，与ancf程序相结合，能够快速而准确的对聚酯缆系泊系统进行设计。
[0049]
为达到以上目的和效果，下面对本方法进行详细说明。
[0050]
ancf计算程序主要分为四大模块：输入参数模块、系泊静态计算模块、系泊动态计算模块、保存结果模块。
[0051]
聚酯缆系泊输入参数模块一共包含五个部分的参数，分别为：
[0052]
1、求解控制参数，迭代步数，结果输出间隔；
[0053]
2、系泊各段的直径、干重、拉伸刚度、弯曲刚度、划分单元数；
[0054]
3、计算工况参数，包括水深、水密度、波高、波浪周期、流速、流向；
[0055]
4、总体的长度以及单元数；
[0056]
5、单元的属性，包括聚酯、钢缆以及铁链。
[0057]
聚酯缆系泊静态计算模块首先采用悬链线理论进行初步的静态计算来得到单元节点的坐标，然后对刚度矩阵进行计算，刚度矩阵包括两个部分：轴向刚度和弯曲刚度。刚度矩阵的积分形式为：
[0058][0059]
其次对弹性力进行计算求解，包括轴向弹性力和弯曲弹性力：
[0060][0061]
考虑粘弹性公式
[0062][0063]
求解的积分方法与刚度矩阵类似。加载基于莫里森公式计算出海流载荷力f以及水下重力，与静力平衡方程联立可得：
[0064]
k(q
(n)
)δq
(n)
＝q
e-qs(q
(n)
)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0065]
静力迭代格式可表示为：
[0066]
δq
(n)
＝(k(q
(n)
))-1
(q
e-qs(q
(n)
))
[0067]q(n+1)
＝q
(n)
+δq
(n)nꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5)
[0068]
聚酯缆系泊动态计算模块需要输入计算总时长，根据虚功原理建立柔性结构动力学方程。首先计算单元各项虚功之和，包括惯性力虚功δwi、粘弹性力虚功δws以及外力虚功δwe。
[0069][0070]
式中，q＝q
e-qs为单元广义力，由单元粘弹性力和外力组成。作用在柔性结构上的外力主要包括集中载荷和分布载荷，其中作用于x
p
处的集中载荷p的虚功和广义力可表示为：
[0071]
δw
ep
＝δr(x
p
)
t
p＝δq
tqep
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(7)
[0072][0073]
对于受约束柔性结构系统，其动力学方程为微分代数方程，具体可表示为如下形式：
[0074][0075]
由于约束方程线性独立，约束雅克比矩阵为行满秩。对于广义坐标数为ns、约束方程数为nc的柔性多体系统，广义坐标可分离为n
s-nc个独立坐标和nc个非独立坐标：
[0076][0077]
其中和分别表示独立坐标和非独立坐标。
[0078]
根据上式，式(9)中雅可比矩阵可以写为:
[0079][0080]
其中为nc×
(n
s-nc)维矩阵，为nc×
nc维矩阵。
[0081]
采用newmark积分求解思想，对式(9)进行变换，可得非线性迭代方程的一般形式为：
[0082][0083]
对于结果的保存，可以选择存储对象的格式，以及计算张力的位置。
[0084]
ancf理论方法形成的质量矩阵为常值对称方阵，离心力和科氏力为零，有利于使用有限元方法编程计算。同时使用斜率代替转角坐标，避免了坐标系转换，简化了计算程序，有限元离散时可看作等参元，因此与有限元方法配合可以有效地对结构进行静、动力分析。
[0085]
多目标函数布谷鸟优化算法主要分为三大模块：原始参数输入以及目标函数设定模块、主程序以及子程序运算模块、基于优化结果可视化后处理模块。
[0086]
原始参数的输入，即将系泊系统原始参数输入到文件中，其中包括水深、每段系泊线的干重、湿重、长度、弹性刚度、以及截面面积。设置各项参数的目的是为了与优化结果进行各项静动力特性对比。目标函数的设定在于，明确设计程序的优化方向，使优化前后结果有一个直观的比较。以原聚酯缆系泊计算的结果为标准，设定目标函数。根据目标函数的定义可以得知，目标函数的值越小，优化结果越接近最优值。
[0087]
布谷鸟算法是一种源于布谷鸟将自己的蛋放到别的鸟巢中孵化的自然现象而衍生出的一种仿生算法。布谷鸟算法是使用发现新巢的概率pa来实现局部随机变量和全局搜索变量的。其中局部随机变量可以写成：
[0088][0089]
其中和是通过随机产生种群中的两个不同的解，h为单位阶跃函数s为局部搜索的步长。通过改变pa值来实现对不同的解的单位阶跃量变化来判断是否为局部最优。
[0090]
全局搜索变量采用的是levy飞行
[0091][0092]
其中
[0093][0094]
α为步长的缩放因子，l为特征尺度并且与缩放因子相互影响。布谷鸟算法的基本步骤如下。
[0095]
步骤1：设置发现鸟巢的概率值(pa)，以及非支配解的选择和淘汰因子；
[0096]
步骤2：将待求参数进行赋值；
[0097]
步骤3：确定鸟巢的初始值并选择非支配解；
[0098]
步骤4：采用莱维飞行对鸟巢位置更新；
[0099]
步骤5：寻找新的鸟巢(新的解)，并确定鸟巢之间是否存在支配解；
[0100]
步骤6：全局搜索非支配解，扩展非支配解的适应度函数取值范围；
[0101]
这里采用轮盘赌选择算子的算法实现全局搜索最优解，其基本思想是每一个个体被选中的概率与其适应度数值的大小成正比，即每个个体的累积概率为：
[0102][0103]
qi为个体的累计概率，p(xj)为每个个体被选中为下一代群体的概率。采用轮盘赌选择算子随机选择非支配解可以有效避免陷入到局部最优。
[0104]
优化程序主要采用的是多目标函数的布谷鸟算法(mocs)，为了更直观的选择最优解，本方法在此基础上加入了帕累托前沿功能(mopcs)。本方法判断优化结果优劣采用的是基于帕累托前沿。在采用后处理可视化对比时，对原系泊系统进行静力以及动力计算，并且画出静力特性曲线以及动力特性曲线。对优化结果中与目标函数误差最小的优化参数同样进行计算，并且与优化前的结果进行对比分析。
[0105]
本发明将布谷鸟优化算法计算出的系泊参数输入至ancf计算软件中，并得出相应的结果，按照此方法进行循环计算，将计算结果按照目标函数与原系泊系统的结果进行对比，寻找最优值。
[0106]
本发明操作简单，界面简洁，采用的布谷鸟算法结合全局最优和局部最优，避免了其它算法容易陷入局部最优的问题。通过不断淘汰支配解，并重新分布非支配解，提高了收敛速度。在后处理方面，判断最优解优劣过程简单明了，且对比的结果全面，保证了最终的优化设计方案的准确性。
[0107]
基于多目标函数布谷鸟优化算法，对某一聚酯缆系泊系统进行优化设计(图1)如下：
[0108]
首先，输入全长系泊系统参数
[0109]
将原长系泊系统的系泊线干重(d)、湿重(w)、长度(l)、刚度(e)、截面面积(a)以及水深参数输入至inputcatenary1.m系泊参数文件中。这里的目标函数为。
[0110]
其次，设置优化参数的上下限，进行优化计算。在优化算法主程序mopcs.m中设置目标函数个数、需要优化的变量数、最大迭代次数、初始种群规模以及系泊系统的优化参数
取值范围(长度、截面面积、湿重)。经多次试验证明，当发现新巢的概率pa为0.25时，效果最佳，因此，默认pa＝0.25。
[0111]
ancf求解静力的主程序为staticanalysis.m，将静力结果保存在staicsolvernr.m中。在程序riserdyn.m、internalforce.m、stiffnessmatrix.m、elementseafloorforce.m、elementhydroforce.m中分别计算重力、弹性力、刚度矩阵、海床力、流体作用力。求解动力主程序为dynamicanalysis.m，并保存结果。
[0112]
在ancf计算程序中重复计算优化算法得出的系泊参数，按照目标函数的误差大小选取最优值，并将最优值参数结果与原有系泊系统进行静动力对比，进一步验证优化参数的准确性。
[0113]
系泊系统的参数取值范围根据优化结果的适应度调整，初始设置较大的范围，然后通过优化结果适当缩小范围。
[0114]
本发明在操作时流程步骤为：
[0115]
步骤1：设置多目标函数以及系泊参数的取值范围；
[0116]
根据目标函数选择优化程序的最优值，多目标函数如下。
[0117][0118][0119][0120]
其中，fit(1),fit(21),fit(3)分别代表优化相关的目标函数，fit(1)代表聚酯段处张力与该段上破断力相关的目标函数，fit(2)代表单根系泊缆优化前后的总体造价相关的目标函数，fit(3)代表单根系泊缆优化前后张力相关的目标函数；ti代表聚酯缆段某点处的张力，fbi代表某点出的破断力，fbi＝170466*d2kn；cj代表直到j点处时的系泊缆总体价格，c为原来系泊参数的总价格；i和j分别代表聚酯缆段和总体系泊缆的节点。根据目标函数可以得知，优化后的结果与原结果相差越小，目标函数的值越小。
[0121]
计算水平力、竖直力、系泊缆张力采用集中质量法。将系泊线的每个点看作节点，通常，除两端点外，节点上的集中质量取为相邻两段系泊线单元质量之和的一半。考虑第j个点在任意方向的运动，设j点x和z方向的分量为由引起的节点的张力为f
nxj
，设其在x、z方向的分力分别为则有以下的关系式。
[0122][0123][0124]
[0125][0126]
式中a
nj
为j点法向附加质量；c
hn
为j点的法向附加质量系数；dc为等效截面直径；为线段的长度；是第(j-1)与第j个集中质量处系泊线倾角的平均值，即ρ为流体密度。根据以上推导，同理可得由引起的法向张力f
nzj
在x、z方向的分力分别为
[0127]
步骤2：产生随机初始化种群以及计算响应的初始适应度；
[0128]
动力程序以ancf理论以及集中质量法理论的不断迭加为前提，通过输入的参数范围计算出各个解集的适应度函数。
[0129]
求解系泊线的动力特性可按照以下过程迭代进行：
[0130]
1.计算静平衡状态下的系泊线形状以及张力，可采用数值方法进行实现；
[0131]
2.给定某点运动，在动力程序中设置多个幅值和频率的正弦波，计算该点运动状态；
[0132]
3.修正离水底最近点的质量，并计算每个点的质量系数；
[0133]
4.计算某点的速度，并依次得到相应张力；
[0134]
5.计算各点相对时间变换的位移量；
[0135]
6.由3-5部分过程迭代至收敛，计算完成。
[0136]
步骤3：确定种群中是否存在支配解并筛选出非支配解；
[0137]
判断支配解的依据为：
[0138]
假设判断标准初始值b＝0，
[0139]
b＝all(fit(1)＜＝fit(2))&any(fit(1)＜fit(2))
ꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(24)
[0140]
如果目标函数满足此情况，则b为1(支配解)，如果不存在此情况，则返回0(非支配解)。选择非支配解的原因是因为非支配集排序是不受目标数量和其他决策变量影响。
[0141]
步骤4：进入主程序循环，扩大种群范围，循环次数为最大迭代次数；
[0142]
调用repmat函数，该函数功能为将原始参数矩阵的扩展到指定行列的矩阵中。将优化参数的取值范围矩阵扩大。
[0143]
步骤5：种群位置更新(莱维飞行)，并扩展适应度函数范围；
[0144]
种群更新的步长是有关种群数目、参数取值范围上下限、以及非支配解的循环过程，调用的是randn函数是均值为0方差为1的标准正态分布。采用轮盘算子法选择非支配解，以避免陷入局部最优。通过非支配解参数范围，以及步长的选取，选择新的种群。并配置新的适应度函数。
[0145]
步骤6：寻找新的解，并继续筛选出非支配解
[0146]
nest＝reshape(nest，[nvar，size(nest，1)])
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(25)
[0147]
运用reshape函数，通过目标函数，按照列的顺序进行转换的，按列存放新的解nest，nvar指的是目标函数的个数。
[0148]
步骤7：判断非支配解数量是否高于种群数量，若高于，则继续循环；若低于，则结束循环并得出帕累托最优解集。输出的部分最优解数据如图6所示。
[0149]
步骤8：选择出帕累托解中适应度最小的一组参数，应用程序对比结果，帕累托前沿生成如图3所示。静力特性主要对比分力和张力的变化曲线过程；动力特性主要对比分力和张力的时历结果。静动力结果如图4、图5所示。
[0150]
优化设计出的结果可以等效于原来的系泊系统，为聚酯缆系泊系统的设计提供了参数的参考范围。
[0151]
以上所述实施例仅是为充分说明本发明而所举的较佳的实施例，本发明的保护范围不限于此。本技术领域的技术人员在本发明基础上所作的等同替代或变换，均在本发明的保护范围之内。本发明的保护范围以权利要求书为准。