一种基于切比雪夫算法的自由曲面网格智能化划分方法与流程

1.本技术涉及建筑网格划分领域，尤其涉及一种基于切比雪夫算法的自由曲面网格智能化划分方法。


背景技术：

2.空间结构在注重建筑美学效果及需要大跨度空间的公共建筑等领域具有明显的优势，在国内外得到了非常广泛的应用。传统空间结构的建筑表面均为可用解析函数表达的平面或简单规则曲面，但难以满足人们对优美建筑的追求。随着计算机科学技术的进步、建筑施工工艺的发展和建筑审美的提高，尤其是进入二十一世纪以来，自由曲面结构以其优美的造型越来越多地出现在人们的视野当中。“自由曲面”指无法用单个或几个解析函数表达的曲面，也可理解为那些明显区别于传统建筑造型的曲面。由于解析曲面具有一定的周期性或规律性，其网格划分是比较方便的。而自由曲面的不规则性，使传统的网格划分对于自由曲面结构来说难以适用。因此，如何在自由曲面上生成线条流畅、大小基本一致的网格，是空间结构领域的热点和难题。
3.国内外学者对自由曲面结构进行了大量研究。bletzinger等将传统的逆吊试验与皂泡法结合，运用结构优化技术对曲面进行优化，结果表明三者结合具有较好的应用前景。高博青等对自由曲面网格划分进行了一系列研究：利用弹簧质点法对自由曲面四边形网格进行平面化处理，高度平面化四边形网格有利于降低工程造价；通过边界曲线分段并连线的办法，生成适应于不同边界及不同曲率曲面的自适应性网格；将复杂自由曲面离散为三角形面片，在面片上进行delaunay三角剖分。李承铭等编制智能化网格设计程序，并运用于上海阳世博轴阳光谷设计。冯若强等同时考虑了自由曲面索支撑空间网格结构的力学、几何、经济指标，进行多目标优化。但目前针对四边形网格，其均匀性和对复杂曲面边界的适应性依然不理想。


技术实现要素：

4.本技术提供一种基于切比雪夫算法的自由曲面网格智能化划分方法，旨在解决现有的自由曲面上生成的网格不均匀的问题。
5.本技术的技术方案是：
6.一种基于切比雪夫算法的自由曲面网格智能化划分方法，包括以下步骤：
7.s1，利用grasshopper的python函数提取曲面s的边界b后，用extend命令将所述曲面s根据设计的比例沿所述边界b中的外边界向外延伸；
8.s2，指定所述曲面s需要划分网格的其中一个曲面，明确其中一个所述曲面上的切比雪夫算法的开始点和目标杆长，并明确所述网格上的x轴与其中一个所述曲面参数域u方向之间的夹角，具体地，其夹角可以由设计人员确定，可默认为0度，从而明确所述网格x轴与y轴之间的夹角，网格的x轴与y轴之间的夹角也为设计人员确定，可默认为90度；并且，开始点和目标杆长均由设计人员确定，目标杆长为期望网格内所有杆件能达到的杆长，由设
计人员定义，一般为3米；
9.s3，基于所述开始点、所述网格的x轴与其中一个所述曲面参数域u方向之间的夹角、所述网格x轴与y轴之间的夹角，所述网格x轴方向、y轴方向上分别生成两列控制点，每列控制点上的空间距离等于所述目标杆长；
10.s4，过x轴方向上的第一个控制点并作半径等于所述目标杆长的第一球体，过y轴方向上的第一个控制点并作半径等于所述目标杆长的第二球体，求所述第一球体与所述第二球体的交线c，然后求所述交线c与所述曲面s的两个交点，其中一个交点为开始点，另一个交点定为第一个网格点；
11.s5，将所述第一球体的原点转化为最新的网格点和x轴方向上的下一个控制点，并按照步骤s4而生成x轴方向上的一系列新网格点；将所述第二球体的原点转化为最新的网格点和y轴方向上的下一个控制点，并按照步骤s4而生成y轴方向上的一系列新网格点；
12.s6，按照步骤s5进行重复操作，从而生成所述网格x轴方向和y轴方向上的所有剩余网格点；
13.s7，用提取的所述曲面s的所述边界b对生成的边界网格进行裁剪；
14.s8，明确杆件长度变化比限值rl，从最大的一个杆件开始，逐步向下搜索杆件，并计算均值和最大长度变化比；当所述杆件长度变化比值r大于限值rl时，将所述杆件划分到同一组中；从下一个杆件开始重新搜寻，直到遍历所有所述杆件；经过分组后，将各组的均值取为该组内每根所述杆件的原长；
15.s9，明确弹簧刚度基数a、b，根据每根所述杆件原长与实际长度明确弹簧刚度；
16.s10，将所述网格上的所述杆件等效为具有原长和弹簧刚度的弹簧，将所述网格节点等效为理想质点，对等效后的弹簧质点系统进行迭代优化。
17.作为本技术的一种技术方案，在步骤s7中，对所述边界网格进行裁剪的具体方法如下：
18.s71，将所述网格节点投影到延伸后的所述曲面s的二维参数域，得到二维参数域点阵{pi}；
19.s72，将所述曲面s的所述边界b对应的二维曲线离散为平面多边形，离散点数为所述网格的边长l控制；
20.s73，使用经典的象限环顾法判断所述二维参数域点阵{pi}中的二维点是否包含在所述多边形内；若所述二维点包含在所述外边界离散的所述多边形内，且不被所述曲面s上的任意一个内边界离散的多边形包含，即所述二维点被标识为内部节点，否则所述二维点被标识为外部节点；
21.s74，明确每一个所述杆件的类别：若所述杆件端点均为外部节点，则所述杆件为外部杆件；若所述杆件端点均为内部节点，则所述杆件为内部杆件；若所述杆件端点一个为内部节点，一个为外部节点，则所述杆件为边界杆件；
22.s75，删除所述外部杆件，保留所述内部杆件，并将所述边界杆件与二维边界的交点投影回所述曲面s，代替被删除的所述外部节点。
23.作为本技术的一种技术方案，在步骤s8中，所述杆件长度变化比由下式确定：
24.25.其中，r为所述杆件长度向量{l}的长度变化比；i为所述杆件的序号；为所述杆件长度向量{l}的均值。
26.作为本技术的一种技术方案，在步骤s9中，所述杆件弹簧刚度由下两式确定：
27.δli＝|l
i-reli|；
[0028][0029]
其中，reli是步骤s2中确定的每根所述杆件的目标杆长；δli为所述杆件的实际长度与所述原长的绝对差值；sti为所述杆件弹簧刚度；st
bench
为所述弹簧刚度基数；a和b均为参数，且a≤1。
[0030]
本技术的有益效果：
[0031]
本技术提供了一种基于切比雪夫算法的自由曲面网格智能化划分方法，其能够实现智能化、参数化划分自由曲面切比雪夫网格，利用边界剪裁算法能使空间切比雪夫网格适应多种曲面形态及边界条件，使用弹簧质点法在切比雪夫内部网格可控、均匀、流畅的基础上尽可能减少杆长分组，能方便切比雪夫网格的设计与施工，同时使得网格布置更美观，具有良好的建筑美学效果。
附图说明
[0032]
为了更清楚地说明本技术实施方式的技术方案，下面将对实施方式中所需要使用的附图作简单地介绍，应当理解，以下附图仅示出了本技术的某些实施例，因此不应被看作是对范围的限定，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他相关的附图。
[0033]
图1为本技术第一实施例提供的原曲面示意图；
[0034]
图2为本技术第一实施例提供的延伸曲面示意图；
[0035]
图3为本技术第一实施例提供的输入参数示意图；
[0036]
图4为本技术第一实施例提供的x轴和y轴方向控制点示意图；
[0037]
图5为本技术第一实施例提供的通过第一球体和第二球体求交得到第一个网格点示意图；
[0038]
图6为本技术第一实施例提供的沿x轴方向生成一系列网格点示意图；
[0039]
图7为本技术第一实施例提供的延伸曲面的网格示意图；
[0040]
图8为本技术第一实施例提供的边界裁剪二维平面示意图；
[0041]
图9为本技术第一实施例提供的边界离散后的平面多边形示意图；
[0042]
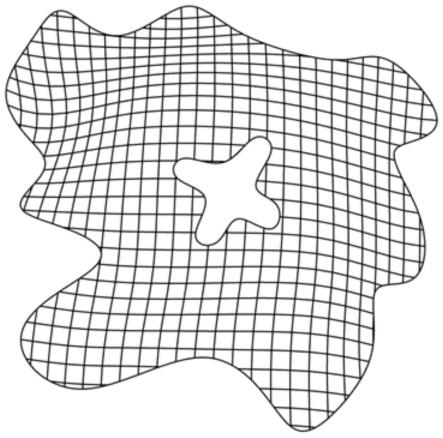
图10为本技术第一实施例提供的裁剪后的网格示意图；
[0043]
图11为本技术第二实施例提供的原曲面示意图；
[0044]
图12为本技术第二实施例提供的裁剪后的网格示意图。
具体实施方式
[0045]
为使本技术实施例的目的、技术方案和优点更加清楚，下面将结合本技术实施例中的附图，对本技术实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是
本技术一部分实施例，而不是全部的实施例。通常在此处附图中描述和展示出的本技术实施例的组件可以以各种不同的配置来布置和设计。
[0046]
因此，以下对在附图中提供的本技术的实施例的详细描述并非旨在限制要求保护的本技术的范围，而是仅仅表示本技术的选定实施例。基于本技术中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本技术保护的范围。
[0047]
应注意到：相似的标号和字母在下面的附图中表示类似项，因此，一旦某一项在一个附图中被定义，则在随后的附图中不需要对其进行进一步定义和解释。
[0048]
在本技术的描述中，需要说明的是，术语“上”、“下”等指示的方位或位置关系为基于附图所示的方位或位置关系，或者是该发明产品使用时惯常摆放的方位或位置关系，仅是为了便于描述本技术和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此不能理解为对本技术的限制。
[0049]
此外，在本技术中，除非另有明确的规定和限定，第一特征在第二特征之上或之下可以包括第一和第二特征直接接触，也可以包括第一和第二特征不是直接接触而是通过它们之间的另外的特征接触。而且，第一特征在第二特征之上、上方和上面包括第一特征在第二特征正上方和斜上方，或仅仅表示第一特征水平高度高于第二特征。第一特征在第二特征之下、下方和下面包括第一特征在第二特征正下方和斜下方，或仅仅表示第一特征水平高度小于第二特征。
[0050]
此外，术语“水平”、“竖直”等术语并不表示要求部件绝对水平或悬垂，而是可以稍微倾斜。如“水平”仅仅是指其方向相对“竖直”而言更加水平，并不是表示该结构一定要完全水平，而是可以稍微倾斜。
[0051]
在本技术的描述中，还需要说明的是，除非另有明确的规定和限定，术语“设置”、“相连”、“连接”应做广义理解，例如，可以是固定连接，也可以是可拆卸连接，或一体地连接；可以是机械连接，也可以是电连接；可以是直接相连，也可以通过中间媒介间接相连，可以是两个元件内部的连通。对于本领域的普通技术人员而言，可以具体情况理解上述术语在本技术中的具体含义。
[0052]
第一实施例：
[0053]
如图1所示，其为自由曲面，下面以该自由曲面为例，说明本技术提供的一种基于切比雪夫算法的自由曲面网格智能化划分方法的具体实现方式。
[0054]
s1，延伸曲面：当自由曲面内部存在空洞或外部边界不规则时，为了保证生成的网格能够铺满曲面，将原曲面延伸一定比例。如图2所示，该曲面中存在一条不规则内边界，一条不规则外边界。利用grasshopper的python函数dupliatesurfaceborder提取曲面s的边界b后，用extend命令将曲面s进行延伸。边界b包括内边界和外边界，此时内边界内的空洞被补齐，曲面沿外边界外伸出一定距离。本步骤能够保证在延伸曲面上生成的网格能够铺满原曲面，方便后续裁剪；
[0055]
s2，确定输入参数s、p、l、r1、r2：为了达到参数化设计的目的，可以通过调节主要输入参数来智能化控制网格形状及长度。如图3所示，其中，(1)s代表原曲面；(2)p代表开始点，其默认值为曲面参数域重点；(3)l代表目标杆件长度，其默认值为3米；(4)r1代表网格x轴与曲面参数域u方向的夹角，其默认值为45
°
；(5)r2代表网格x轴与y轴之间的夹角，其默
认值为90
°
；
[0056]
s3，在延伸曲面上使用切比雪夫算法生成四边形网格：本实施例中，采用切比雪夫算法在延伸曲面上生成均匀的四边形网格，具体方法如下：
[0057]
s31，基于输入参数，在x轴和y轴方向上生成两列控制点，如图4所示，在曲面s上，基于开始点p，首先在与曲面s二维参数域u方向成夹角r1的方向，即网格的x轴方向，生成一系列空间距离为l的控制点；然后在与x轴方向成夹角r2的方向，即网格的y轴方向，生成一系列空间距离为l的控制点；
[0058]
s32，生成第一个网格点n1：如图5所示，过x轴方向上的第一个控制点作半径为l的第一球体，过y轴方向上的第一个控制点作半径为l的第二球体，求第一球体和第二球体的交线c，然后求交线c与曲面s的两个交点；由空间球体的性质可知，该两个交点中一个为开始点p，一个为新的网格点n1；
[0059]
s33，沿x轴和y轴方向生成一系列网格点：如图6所示，将第一球体的原点变为最新的网格点和x方向的下一个控制点，重复步骤s32，即可生成x轴方向的一系列新网格点；将第二球体的原点分别变为最新的网格点和y轴方向的下一个控制点，重复步骤s32，即可生成y轴方向的一系列新网格点；
[0060]
s34，重复步骤s33，生成x轴和y轴方向的所有剩余网格点，如图7所示；
[0061]
s4，对曲面边界处的网格进行裁剪：在曲面边界处由于曲面曲率较大，延伸后的网格并不会与边界线b相交；如图8所示，虚线部分代表延伸部分曲面，在延伸部分曲面的网格不会与原边界线b相交，要对网格进行裁剪则必须求出网格与边界线b的交点；本实施例中，采用下述方法进行裁剪：
[0062]
s41，将网格节点投影到延伸后曲面的二维参数域，得到二维参数域点阵{pi}；
[0063]
s43，将曲面边界b对应的二维曲线离散为平面多边形：如图9所示，该曲面具有两条及以上的曲面边界，此时需考虑所有曲面边界，边界可分为一条内边界与一条外边界；二维曲线离散为平面多边形时的离散点数应根据离散点的空间距离划分；可按离散点的空间距离为网格的边长l控制，进行二维边界曲线的离散；此法可保证后续算法简洁高效运行；
[0064]
s43，对点阵{pi}的每个二维点进行多边形包含判断：使用经典的象限环顾法判断二维点是否包含在多边形内；对于每个二维点，若其包含在外边界离散的多边形内，且不被任意一个内边界离散的多边形包含，即标识为内部节点，否则该节点为外部节点；
[0065]
s44，标识边界杆件：网格中存在三类杆件，第一类杆件为外部杆件，杆件端点均为外部节点；第二类杆件为内部杆件，杆件端点均为内部节点；第三类杆件为边界杆件，杆件端点一个为内部节点，一个为外部节点；
[0066]
s45，处理杆件：根据s44中的杆件分类，删除外部杆件，保留内部杆件；将边界杆件与二维边界曲线的交点投影回空间曲面，代替被删除的外部节点；
[0067]
经过s4中的以上五步，即可得到裁剪完成的空间切比雪夫网格，如图10所示；该算法的底层步骤为空间点的投影、平面点的多边形包含判断及二维边界杆件的求交运算；
[0068]
s5，杆长优化：采用边界裁剪算法可以使空间切比雪夫网格适应多种曲面形态及边界条件，网格整体流畅均匀，内部杆件的长度高度一致；但可以看到，在曲面边界处，有大量杆件长度不一致；由于曲面边界的随机性，很难通过调整输入参数来控制曲面边界附近杆件长度；本实施例结合弹簧质点法优化边界附近杆件杆长；弹簧质点法基本思想为将网
格杆件等效为具有原长和弹簧刚度的弹簧，将网格节点等效为理想质点，对等效后的弹簧质点系统进行迭代优化；弹簧质点系统中，弹簧倾向于恢复到其预定原长，而同属于一个质点的弹簧倾向于恢复到一条直线；使用弹簧质点法进行杆长优化，其关键在于如何确定杆件原长及弹簧刚度；具体步骤如下：
[0069]
s51，确定杆件原长：对于一组杆件长度向量{l}，定义其长度变化比为：
[0070][0071]
其中，r为杆件长度向量{l}的长度变化比，i为所述杆件的序号；为长度向量{l}的均值；确定长度变化比限值rl为10％；从最大的一个杆件开始，逐步向下搜索杆件，并计算杆件长度的均值和最大长度变化比；当杆件长度变化比r大于限值rl时，将该类杆件视为同一组；然后从下一个杆件开始，重新搜寻，直到遍历所有杆件；经过分组后，将各组的均值取为该组内每根杆件的原长；此方法可保证每一组的杆件均向原长优化，且最大杆长变化率不超过rl，保证了切比雪夫网格经过杆长优化后不会偏离以前的几何形状太多；
[0072]
s52，确定弹簧刚度：不同的弹簧刚度决定了杆件之间恢复到原长的恢复力大小；相对于弹簧刚度小的杆件，弹簧刚度较大的杆件更能够恢复到原长，并将其长度保持在原长附近；本实施例中采用对数方法确定杆件弹簧刚度：
[0073]
δli＝|l
i-reli|；
[0074][0075]
其中，reli是s51中确定的每根杆件的原长，δli为杆件长与原长的绝对差值，sti为杆件弹簧刚度，st
bench
为弹簧刚度基数，a(≤1)和b为参数；本例中取st
bench
为50、a为0.1、b为0.03m；一般情况下a需取小于1的值，这样保证与原长接近的杆件刚度相对较大；若a取大于1的值，则与原长差距较大的杆件刚度较大，接近原长的杆件刚度较小，与杆长优化目标相违；
[0076]
s53，杆长优化：确定了杆件长度和杆件弹簧刚度后，利用grasshopper中的springs组件，将裁剪后的切比雪夫网格等效为弹簧质点系统；利用grasshopper平台中的kangaroo组件，进行迭代优化；优化过程中还需用curvepull组件和pulltosurf组件，将边界上的网格点和曲面上的网格点约束在边界和曲面上。
[0077]
本例中优化前杆件数量为1266，经过杆长优化后，杆件种类由原来的121种大幅下降为43种；可以看到杆长优化后的切比雪夫网格仍然能在边界处保持其均匀流畅的特点。整个划分包括杆长优化过程仅需7.9s(64位系统windows7系统，英特尔i7-6700 cpu，3.40ghz，24.0gb内存)。
[0078]
第二实施例：
[0079]
本实施例中，对图11所示的曲面进行网格划分，该曲面有一条内边界，一条外边界。利用本技术中的前述方法对其进行处理后(具体做法如前所述，不再赘述)，生成网格如图12所示。
[0080]
本例中优化前杆件数量为1503；取rl为10％、st
bench
为50、a为0.1、b为0.03m；经过杆长优化后，杆件种类从189种大幅下降为36种；其体现了杆长优化的有效性。整个划分包
括杆长优化过程所需时间为120.1s(64位系统windows7系统，英特尔i7-6700 cpu，3.40ghz，24.0gb内存)。
[0081]
以上所述仅为本技术的优选实施例而已，并不用于限制本技术，对于本领域的技术人员来说，本技术可以有各种更改和变化。凡在本技术的精神和原则之内，所作的任何修改、等同替换、改进等，应包含在本技术的保护范围之内。