一种连续索的非线性滑移计算方法与流程

1.本发明属于桥梁动力学技术领域，涉及一种连续索的非线性滑移计算方法。


背景技术：

2.索作为空间结构重要的组成部分之一，其小自重、高效率、大跨度、省成本的优点，使其在张弦梁、缆索系统、弦支穹顶等轻型高效结构中占有重要的地位，广泛应用于大型体育馆屋面结构、斜拉桥、风景区游览索道以及拉索塔架等。连续索在节点处的连接有两种形式：一种是索和节点固定，节点两侧的索段在节点处不发生滑移；另一种是索在节点处采用穿管、滑轮等连接方式，索和节点之间能发生相对滑移。第二种连接形式称为接触连接，对应的节点称为接触点。第二种索连接形式无论是在张拉成型的施工阶段或施工完成后的使用阶段，始终无法避免索的滑移运动问题及在滑移过程中存在的多种滑移状态难题。
3.目前，针对滑移索单元的研究主要有以下几种方法：1)推导单个索段的滑移刚度来考虑索段滑移的影响，但需求解复杂的滑移刚度影响矩阵，且只对中间节点进行了求解，不便于扩展到多跨连续索结构中；2)利用线弹性理论推导单折点力筋单元，但是忽略了拉索的垂度，且将非线性问题线性化，使用范围受到限制，也不便于结构的受力全过程分析；3)滑移索系结构的冷冻升温法通过现有的有限元工具，通过虚加温度荷载的办法，来解决在加载过程中索的滑移问题，但是收敛速度不易控制；4)还有的索滑移的算法在求解各索段的原长时采用了不考虑弹性的索长计算式，对水平投影和竖直投影的修正也是非必要的；5)还有引入弯矩分配法概念，但采用的是二节点直线杆单元来代替索单元，不适用于大垂度索结构；6)还有用弹性悬链线单元模拟索段推导索在支撑点处的单侧滑移刚度，通过有限元迭代调整支撑点两侧的索原长，使索力相等，为了模拟索的滑移，采用通用有限元软件中的接触单元，但这种方法非常复杂且工作量很大。


技术实现要素：

4.本发明的目的在于克服现有技术中在考虑索段滑移的影响的计算时，存在设计方法复杂、适用性窄、计算环节不易收敛等上述不足，提供一种连续索的非线性滑移计算方法。
5.为了实现上述发明目的，本发明提供了以下技术方案：
6.一种连续索的非线性滑移计算方法，包括如下步骤：
7.a、根据索结构的几何参数、材料参数和边界条件，将索与所有滑轮的连接均视为接触连接建立有限元模型，以索分别在1
#
,2
#
,...,i
#
滑轮滑移单位长度的情况下求解1
#
,2
#
,...,i
#
滑轮两侧索段的力差向量，获得滑移刚度影响矩阵：
8.其中k
i,1
表示以1
#
滑轮滑移单位长度时i
#
滑轮两侧索段的力差向量，以此类推；
9.b、结合1
#
,2
#
,...,i+1
#
索段的无应力长度，对索结构进行几何非线性分析，获取1
#
,2
#
,...,i+1
#
索段的力差向量得到第一力差向量其中，1
#
,2
#
,...,i+1
#
索段的初始无应力长度按照跨径比例分配，1
#
滑轮两侧分别为1
#
索段和2
#
索段，t1表示1
#
滑轮两侧1
#
索段和2
#
索段的力差向量，以此类推；
10.c、根据公式δl
slide
＝k
slide-1
·
δt求解1
#
,2
#
,...,i
#
滑轮的滑移长度向量δl
slide
＝[δl
1 δl
2 ... δli]
t
，修正各索段的无应力长度并重复步骤a-b得到第二力差向量
[0011]
d、重复步骤a-c，直至||(δt
(n)-δt
(n-1)
)/δt
(n-1)
||≤δε，n表示迭代次数，提取对应有限元模型中的索的位移和各断面的内力，完成滑移计算。
[0012]
优选的，δε＝0.0001-0.0005。
[0013]
优选的，索结构的几何参数包含索的初始拟定截面尺寸、索的截面形状、各索段的跨径和各滑轮之间的高差，材料参数包含索的弹性模量、容重、抗拉强度和最小破断拉力。
[0014]
优选的，几何非线性分析方法为牛顿-拉夫森迭代方法。
[0015]
与现有技术相比，本发明的有益效果：综合利用索的无应力总长度不变和索滑移刚度影响矩阵原理，通过几何非线性求解滑轮两侧索段的力差向量，并根据滑轮两侧的力差向量反复迭代模拟索滑移过程，以此建立连续非线性滑移索单元计算，根据力差向量、滑移刚度影响矩阵和变形向量的关系，求解各滑轮的变形向量，以此更新各滑轮两侧索段的无应力长度，再重新计算滑轮两侧力差向量，并结合滑移刚度影响矩阵，重新调整滑移点两侧索无应力长度情况，以此循环直至滑轮两侧力差向量收敛。本方法在进行有限元建模时考虑了结构的几何非线性问题和拉索垂度问题，适应于多种工况和不同结构形式连续索计算，相较于现有技术仅适应于单跨拱桥，本方法可适应于多跨连续索和大垂度的结构计算，也可以适合穹顶、悬索桥和拱桥等的计算，而且可以同时考虑主索、牵引索、起重索各索组合作用下结构受力，更贴近工程实际施工，且对无应力长度的初始值依赖性小，无应力索长初始值只要不为负值就都能收敛，收敛更容易，计算效率更高。
附图说明
[0016]
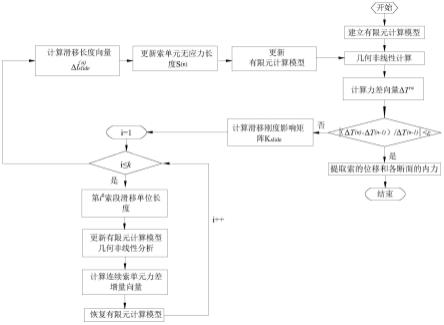
图1是本发明的一种连续索的非线性滑移计算方法的流程图；
[0017]
图2是实施例1中的索鞍结构的结构示意图。
具体实施方式
[0018]
下面结合实施例及具体实施方式对本发明作进一步的详细描述。但不应将此理解
为本发明上述主题的范围仅限于以下的实施例，凡基于本发明内容所实现的技术均属于本发明的范围。
[0019]
实施例1
[0020]
一种连续索的非线性滑移计算方法，如图1所示，包括如下步骤：
[0021]
a、根据索结构的几何参数、材料参数和边界条件，将索与所有滑轮的连接均视为接触连接建立有限元模型，以索分别在1
#
,2
#
,...,i
#
滑轮滑移单位长度的情况下求解1
#
,2
#
,...,i
#
滑轮两侧索段的力差向量，获得滑移刚度影响矩阵：
[0022]
其中k
i,1
表示以1
#
滑轮滑移单位长度时i
#
滑轮两侧索段的力差向量，以此类推；
[0023]
b、结合1
#
,2
#
,...,i+1
#
索段的无应力长度，对索结构进行几何非线性分析，获取1
#
,2
#
,...,i+1
#
索段的力差向量得到第一力差向量其中，1
#
,2
#
,...,i+1
#
索段的初始无应力长度按照跨径比例分配，1
#
滑轮两侧分别为1
#
索段和2
#
索段，t1表示1
#
滑轮两侧1
#
索段和2
#
索段的力差向量，以此类推；
[0024]
c、根据公式δl
slide
＝k
slide-1
·
δt求解1
#
,2
#
,...,i
#
滑轮的滑移长度向量δl
slide
＝[δl
1 δl
2 ... δli]
t
，修正各索段的无应力长度并重复步骤a-b得到第二力差向量
[0025]
d、重复步骤a-c，直至||(δt
(n)-δt
(n-1)
)/δt
(n-1)
||≤δε，n表示迭代次数，提取对应有限元模型中的索的位移和各断面的内力，完成滑移计算。
[0026]
具体的，以图2的索鞍结构为例，图中共设有1
#
、2
#
、3
#
和4
#
滑轮，1#滑轮两侧分别为1
#
和2
#
索段，2
#
和3
#
滑轮之间为3
#
索段，4
#
滑轮两侧分别是3
#
和4
#
索段，根据索结构的几何参数包含索的初始拟定截面尺寸、索的截面形状、各索段的跨径和各滑轮之间的高差，材料参数包含索的弹性模量、容重、抗拉强度和最小破断拉力，将索与所有滑轮的连接均视为接触连接建立有限元模型，设定1
#
滑轮的滑移单位长度，获取1
#
滑轮、2
#
滑轮、...、i
#
滑轮对应两侧索段的索力差分别为k
1,1
、k
2,1
、...、k
i,1
，以各滑轮右侧索力减去左侧索力为索力差，比如1
#
滑轮在滑移单位长度时，1
#
滑轮右侧索力减去左侧索力的值为k
1,1
，2#滑轮右侧索力减去左侧索力的值为k
2，1
，以此类推得到相邻索段的力差向量{k
i1
}，即{k
i,1
}＝[k
1,1 k
2,1 ... k
i,1
]
t
，同理i
#
滑轮滑移单位长度时，各滑轮的相邻索段的力差向量为{k
i,i
},即{k
i,i
}＝[k
1,j k
2,j ... k
i,i
]
t
，以此获得滑移刚度影响矩阵：
[0027][0028]
各索段初始无应力长度按照跨径比例分配，如图中的1
#
索段的无应力长度2
#
索段的无应力长度以此类推，s为索的总长，然后进行几何非线性分析，如采用牛顿-拉夫森迭代算法或弧长法。为方便计算，以滑轮右侧索力减去左侧索力大于零为正、小于零为负，如1
#
滑轮右侧索力减去左侧索力为下标1为1#滑轮，上标1为首次迭代，2
#
滑轮对应的索力差为...，i
#
滑轮对应的索力差为以此形成的第一力差向量
[0029]
根据k
slide
·
δl
slide
＝δt，那么首次迭代求解滑移长度向量即为如本实施例中则根据总索长s不变，对各个索段的无应力长度进行调整如下：
[0030]
，
[0031]
之后代入步骤a-b中更新有限元模型和无应力长度，再次进行几何非线性分析，得到第二力差向量
[0032]
若||(δt
(2)-δt
(1)
)/δt
(1)
||≤δε，取δε＝0.0001-0.0005，则提取当前有限元模型中的索的位移和各断面的内力，完成滑移计算。
[0033]
若||(δt
(2)-δt
(1)
)/δt
(1)
||＞δε，则重复步骤a-c，获取并得到δt
(3)
，以此类推，直至||(δt
(n)-δt
(n-1)
)/δt
(n-1)
||≤δε达到收敛，进而获取收敛模型中的索的位移和各断面的内力。
[0034]
以上仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到变化或替换，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应以的权利要求的保护范围为准。