基于多元正态分布函数的滑坡体系可靠度计算方法

1.本发明属于滑坡评估技术领域，具体涉及基于多元正态分布函数的滑坡体系可靠度计算方法。


背景技术：

2.滑坡稳定的体系可靠度是滑坡可靠性的概率度量，由于岩土体材料的非均质性，滑坡体往往存在大量的潜在滑动面，任一滑动面失效均会导致滑坡系统失效，是一个典型的串联体系可靠度问题。
3.体系可靠度是一个典型的高维度数值积分计算问题，其根本问题在于求解多维数值积分，积分维度与滑动面的数量有关。由于维度增加，多元累计分布函数的积分计算复杂，甚至难以求解。目前对于体系可靠度的计算没有很好的直接求解方法，大多为点估计法或区间估计法，计算效率低，精度不够。


技术实现要素：

4.本发明目的在于针对上述问题，将体系可靠度中存在的多元正态累积分布函数转换为多个二元正态概率乘积的积分形式，直接求解计算，有效解决了高维积分难以求解的问题，通过变量重排序提高计算结果的准确性。
5.为解决上述技术问题，本发明采用的技术方案为基于多元正态分布函数的滑坡体系可靠度计算方法，包括以下步骤：
6.s1：分析确定滑坡体系的失效模式；
7.s2：选择确定滑坡体系各失效模式的功能函数；
8.s3：计算各失效模式的相关性，得到协方差矩阵；
9.s4：推导得到多元正态分布函数在二元条件下的数值积分表达式；
10.s5：对积分变量排序，选择合适的数值积分顺序；
11.s6：根据协方差矩阵和排序后的多元正态分布函数的二元数值积分表达式，计算得到滑坡体系可靠度。
12.优选的，所述步骤s1中滑坡体系的失效模式为导致边坡失去稳定性的任意滑动面。
13.优选的，所述步骤s2中失效模式的功能函数为：
14.z＝f-1
ꢀꢀꢀ
(1)
15.式中：z为滑动面的功能函数，f为滑动面的安全系数。
16.优选的，所述步骤s2中响应面函数为：
[0017][0018]
式中g(x)表示功能函数，a、bi,i＝1,2,
…
n、ci,i＝1,2,
…
n、d
ij
,i＝1,2,
…
n,j＝1,2,
…
n分别表示待定系数；xi,i＝1,2,
…
n、xj,j＝1,2,
…
n表示不同的随机变量；
[0019]
实验点可以沿坐标轴在均值点μ
x
附近选择，其中沿坐标xi轴的实验点具有坐标
其中f＞0是一任意因子。
[0020]
初始迭代点
[0021]
式中x表示随机变量组成的向量；i＝1,2
…
n表示随机变量的初始迭代点；初次计算取平均值，根据式(2)计算得到线性方程组的系数a、bi、ci。
[0022]
优选的，所述步骤s3中各失效模式功能函数之间的协方差计算方式如下：
[0023]
对于非正态变量，按下式进行当量正态化：
[0024][0025][0026]
式中表示当量正态化变量的均值和标准差；为验算点；为累积分布函数，为概率密度函数；φ-1
()表示累计分布函数的逆函数；表示密度函数；
[0027]
功能函数z
l
的均值和标准差分别按下式计算：
[0028][0029][0030]
表示变量均值；表示变量标准差；
[0031]
定义变量xi的灵敏度系数为：
[0032][0033]
式中表示点x
*
与标准化空间中原点o的夹角；
[0034]
式(7)表示在标准正态随机变量y空间的法线式超平面方程，法线为极限状态面上的p
*
到标准正态化空间中原点o的连线，其方向余弦为p
*
表示x空间中的x
*
点在极限状态面的对应点；
[0035][0036]
式中c
jk
表示滑面j、k功能函数之间的协方差；分别表示滑面j、k功能函数的方向余弦；分别表示滑面j、k功能函数的标准差；
[0037]
两个不同滑动面之间的协方差计算步骤如下：
[0038]
(1)假定初始验算点x
*
，一般取x
*
＝μ
x
；
[0039]
(2)当量正态化：利用式(3)、(4)计算和
[0040]
(3)利用式(6)计算不同功能函数的标准差
[0041]
(4)利用式(7)计算不同滑动面的
[0042]
(5)利用式(8)计算不同滑面之间的协方差，此时不同滑动面之间的相关性系数
[0043]
(6)根据步骤(5)得到协方差矩阵σ。
[0044]
优选的，所述步骤s4中确定多元正态分布函数在二元条件下的数值积分形式步骤如下：
[0045][0046]
q2(x；μ,σ)＝(x-μ)
t
∑-1
(x-μ)
ꢀꢀꢀ
(10)
[0047]
式中f()表示密度函数；μ表示变量均值；
[0048]
式中：
[0049]
其中x＝(x1,
…
,xn)
t
为n维随机变量，μi，σ
ii
分别表示变量x＝(x1,
…
,xn)
t
的均值和方差，σ
ij
为变量xi，xj之间的协方差,1≤i《j≤n；
[0050]
考虑一般的多元正态分布函数积分形式如下：∫af(x)g(x)dx；
[0051]
式中x＝(x1,x2,
…
xn)
t
∈rk，a∈rk,dx＝dxndx
n-1
…
dx1，f(x)为多元正态分布函数的密度函数，g(x)为一个应用确定的期望函数，为了简化计算，取g(x)＝1，因此积分区域a为一个超矩形；
[0052]
其中：[a,b],-∞≤ai≤bi，i＝1,
…
k。
[0053]
相应的多元正态分布函数积分形式为：
[0054][0055]
将矩阵σ进行乔里斯基分解，∑＝cc
t
，其中c是一个下三角矩阵，于是x
t
∑-1
x＝x
t
c-t
c-1
x，将变量x用关系式x＝cy替换，于是x
t
∑-1
x＝y
t
y；由于c是下三角结构，函数φn(a,b；∑)的积分区域变为以下形式：
[0056]
a1/c
11
≤y1≤b1/c
11
，(a
2-c
21
y1)/x
22
≤y2≤(b
2-c
21
y1)/c
22
。
[0057][0058]
令令
[0059]
函数φn可以写成以下形式：
[0060][0061]
多元这正态分布函数的一元积分方法的关键在于替换(12)式中yi的值，定义一维截断期望值e如下:
[0062][0063]
式中x表示积分变量，符号φ，φ表示正态分布的概率密度函数和累积分布函数；
[0064][0065][0066]
令j＝1,
…
i-1替换a
′i(y1,
…
,y
i-1
)，b
′i(y1,
…
,y
i-1
)中yi的值，得到最后得到多元正态分布函数一元数值积分问题的近似值如下：
[0067][0068]
上述公式得到了多元正态分布函数的一元数值积分形式，下面给出多元正态分布函数的二元数值积分形式的推导过程；
[0069]
将协方差矩阵∑进行ldl
t
分解，如果n为偶数，矩阵l，d形式如下：
[0070][0071]
其中di,l
i,j
为二阶矩阵，o2为二阶零矩阵，如果n为奇数，则矩阵l中多了一行，且矩阵d中最后一列为d
nn
；
[0072]
将协方差矩阵∑按下面方式分块：
[0073]
其中∑
1.1
为二阶矩阵，d1＝∑
1.1
，r表示σ矩阵中与∑
1.1
相对应的子块；
[0074]
对进行同样的分解过程；
[0075]
通过上述分解过程得到了l,d,通过一种变换x＝ly，于是得到dx＝|l|dy，a≤ly≤b，
[0076]
定义(α,β)j＝(a-g,b-g)j其中令y
2k
＝(y
2k-1
,y
2k
)
t
，得到多元正态分布函数二元数值积分形式如下：
[0077][0078]
令d
ii
表示d矩阵第i行第i列的元素；
[0079]
于是上式可以写为：
[0080]
[0081]
式中zi,i＝1,
…
n表示变量；ω
12
,
…
ω
2k-1,2k
分别表示ρ1,
…
ρk的扩充矩阵；
[0082][0083]
ρk表示对应d矩阵的第k个简化变量；
[0084]
定义最外层二元正态分布(bvn)函数积分形式为p1＝φ2((a
′1,a
′2),(b
′1,b
′2)；ω
12
)，为了逼近内积分，需要得到z1,z2的值，根据利用多元正态分布函数的一元数值积分算法可知z1,z2为截断的双变量分布中变量的期望值；
[0085]
式中p1表示二元正态分布函数数值积分；φ2()表示二元正态分布函数；
[0086]
令在ai＝-∞的情况下，截断的二元正态分布函数的期望值u1,u2如下：
[0087][0088]
式中ρ1表示对应d矩阵的第1个简化变量；q1表示ρ1的替代变量；u、v都是均值变量；
[0089]
上述公式中的u1由下面公式计算得出：
[0090][0091]
计算u2除了a
′1与a
′2互换，b
′1与b
′2互换，其余与计算u1的公式相同；
[0092]
通过公式来近似第二个外层二元正态分布函数积分，其中，为a
′i，b
′i的值，z1,z2由u1,u2代替，再令ρ2表示对应d矩阵的第2个简化变量；q2表示ρ2的替代变量；
[0093]
于是得到
[0094][0095]
并由公式(20)计算得出，计算得到的u3,u4值替换相应的z3,z4的值，于是得到第i步计算公式
[0096][0097]
式中：为a
′i，b
′i的值，z1,
…z2i-2
由期望值u1,
…u2i-2
代替；
[0098]
在经过第k步计算后得到多元正态分布函数的二元数值积分计算公式：
[0099][0100]
优选的，所述步骤s5对积分变量排序，选择合适的数值积分顺序步骤如下；
[0101]
通过改变变量的优先级，对变量进行排序，使最内层积分变量具有较小的期望值；通过选择变量i来选择最外层积分变量；
[0102][0103]
将积分限，∑中行和列的第一个变量和第i个变量进行互换，然后计算∑的
cholesky分解中c的第一列为令令
[0104][0105]
将积分上下限，∑中行与列以及c
12
与c
i1
进行互换，然后计算∑的乔里斯基分解中c的第二列为
[0106][0107]
令
[0108]
到第j步，第j步的积分变量通过挑选变量i来决定，如下式：
[0109][0110]
将积分上下限，∑中行与列，及c中第i行与第j行进行互换，然后计算c的第j列为将积分上下限，∑中行与列，及c中第i行与第j行进行互换，然后计算c的第j列为
[0111]
令
[0112]
式中表示aj的替代变量；表示bj的替代变量；μj、μm分别表示根据式(15)计算得到的期望值；
[0113]
当j＝n整个变量排序过程结束；
[0114]
优选的，所述步骤s6协方差矩阵和排序后的多元正态分布函数的二元数值积分表达式计算滑坡体系可靠度如下：
[0115]
设第i个失效模式发生的事件表示为ei，不发生的事件表示为体系失效事件表示为e，体系可靠事件表示为
[0116][0117]
由式(26)计算得到体系可靠概率。
[0118][0119]
式中：pr,为体系可靠概率。
[0120]
本发明的有益效果是：
[0121]
1.适用性较强：本发明考虑了失效模式之间的相关性，失效模式间的相关性对体系可靠指标有一定影响，如果不考虑失效模式之间的相关性，边坡体系可靠度将会被低估。
[0122]
2.精度高：本发明通过直接求解高维度数值积分，在一定程度上比传统的区间估计法更加准确，通过变量排序进一步有效提高了计算精度。
[0123]
3.效率高：本发明算法有效的避免了多元累计分布函数的复杂高维数值积分，在
给定基本参数后可直接进行计算，大大提高了计算效率。
附图说明
[0124]
下面结合附图和实施例对本发明作进一步说明。
[0125]
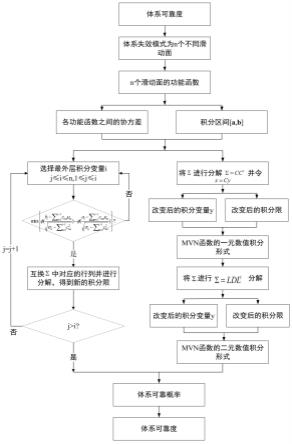
图1为本发明实施例的流程示意图。
[0126]
图2为本发明的计算实例图。
具体实施方式
[0127]
如图2，以经典算例为例来说明本发明的具体实施方式。本发明为一种基于多元正态分布函数的滑坡体系可靠度计算方法，其流程图如图1所示。
[0128]
本发明选取的计算实例如图2所示，土体参数如表1所示。
[0129]
表1土体参数表
[0130][0131][0132]
其余尺寸见图2。
[0133]
实施例的滑坡体系可靠度计算方法包括以下步骤：
[0134]
s1：分析确定滑坡体系的失效模式：假定失效模式为任意滑动面。
[0135]
s2：选择确定滑坡体系各失效模式的功能函数步骤如下：
[0136]
失效模式的功能函数为z＝f-1。根据响应面法计算得到失效模式的功能函数，响应面函数设为
[0137][0138]
利用不同实验点数据，联立方程求解，得到修正系数a，bi，ci。
[0139]
不同滑动面功能函数修正系数如表2所示。
[0140]
表2功能函数修正系数表
[0141]
系数滑动面1滑动面2滑动面3a-0.99248-0.95641-1.4408b10.0493660.0049430.003185b200.0178590.009424b3000.015832c
1-0.0001-1.2e-6-2.4e-6c202.97e-5-4.5e-5c300-3.2e-5
[0142]
s3：计算各失效模式的相关性，得到协方差矩阵，具体过程如下：
[0143]
(1)假定初始验算点x
*
，一般取x
*
＝μ
x
；
[0144]
(2)当量正态化：利用式(3)、(4)计算和
[0145]
(3)利用式(6)计算不同功能函数的标准差
[0146]
(4)利用式(7)式计算不同滑动面的
[0147]
(5)利用式(8)计算不同滑动面之间的协方差，此时不同滑动面之间的相关性系数
[0148]
(6)根据步骤(4)得到协方差矩阵∑。
[0149]
步骤(3)、(4)计算的如表3所示。
[0150]
表3不同滑动面标准差、均值、敏感系数和可靠度
[0151][0152][0153]
计算得到的协方差矩阵σ以及相关性系数如下：
[0154][0155]
相关性系数：ρ
12
＝0.5305，ρ
13
＝0.3184，ρ
13
＝0.3774。
[0156]
s4：推导得到多元正态分布函数在二元条件下的数值积分表达式。
[0157]
s5：对积分变量排序，选择合适的数值积分顺序计算步骤如下：
[0158]
为了提高计算精度和效率，需要对积分变量进行排序；通过置换变量来最小化外部积分。
[0159]
先将矩阵∑进行乔里斯基分解，∑＝cc
t
，为了使外部积分最小，需要使外部积分期望值最小。利用式(13)计算期望e；为了简化计算过程，通过选择变量i来选择最外层积分变量。
[0160]
首先选择第一层积分变量，当1≤i≤n时，
[0161][0162]
然后将第i个积分变量对应的积分限与第一个变量对应的积分限互换；∑中第i行与第一列互换，第i列与第一列互换。
[0163]
然后令
[0164]
得到矩阵c的第一列；
[0165]
令得到最外层积分期望
[0166][0167]
选择第二层积分变量，此时2≤i≤n，
[0168][0169]
将第二个和第i个变量对应的积分限，∑中的行、列进行互换；将第二列中的c
12
和c
i2
互换。
[0170]
令
[0171]
得到矩阵c的第二列；此时
[0172][0173]
以此类推，当j≤i≤n，
[0174][0175]
按照上述步骤进行互换，此时第j个积分变量对应的积分限
[0176][0177][0178]
期望
[0179]
当j＝n时，整个变量排序的过程结束；
[0180]
s6：根据协方差矩阵和多元正态分布函数二元数值积分表达式计算滑坡体系可靠度如下：
[0181]
设第i个失效模式发生的事件表示为ei，不发生的事件表示为体系失效事件表示为e，体系可靠事件表示为
[0182][0183]
pr为体系可靠概率。
[0184]
考虑计算的范围为
[0185][0186]
b＝[+∞,+∞,+∞]
t
，计算得到体系可靠概率为pr＝0.3871。
[0187]
可靠概率pr与体系可靠度β的关系为pr＝φ(β)，得到体系可靠度β＝0.6507。
[0188]
以上所揭露的仅为本发明的具体实施方式，但本发明的具体保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到的变化或变形，都应该涵盖在本发明的保护范围之内。