一种基于准动态的亚格子动能方程模型的大涡模拟方法

1.本发明涉及流体力学技术领域，尤其涉及一种准动态的亚格子动能方程模型的大涡模拟方法。


背景技术：

2.大涡模拟已经被广泛应用于复杂的工程计算以及机理分析中。在大涡模拟中，对navior-stokes方程进行滤波，得到的滤波后的方程会产生一些未封闭项，对这些未封闭项进行建模以完成方程的封闭，而构建的这些模型统称为亚格子模型。目前大部分的大涡模拟的亚格子模型是基于不可压缩情况下推导得到，再推广到可压缩的形式。目前的大涡模拟模型多数是从不可压缩流动的方程出发进行推导，使得在应用于可压缩流动中存在各种各样的问题。


技术实现要素：

3.鉴于此，为解决现有技术中的问题，本发明提出了一种准动态的亚格子一方程模型。本发明从可压缩的方程出发，推导了一种适用于可压缩流动的大涡模拟模型，即准动态的亚格子动能一方程模型。本发明直接从可压缩流动的方程角度出发推导大涡模拟的亚格子模型，有助于解决可压缩流动中的问题，比如预测转捩等；可压缩流动广泛存在于航空航天发动机等复杂内流中，本发明针对可压缩流动提出大涡模拟模型，可帮助解决高超声速转捩预测等等问题。
4.一种基于准动态的亚格子动能方程模型的大涡模拟方法，包括如下步骤：
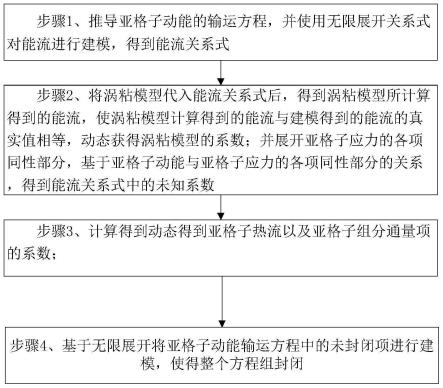
5.步骤1、推导亚格子动能的输运方程，并使用无限展开关系式对能流进行建模，得到能流关系式；
6.步骤2、将涡粘模型代入能流关系式后，得到涡粘模型所计算得到的能流，使涡粘模型计算得到的能流与建模得到的能流的真实值相等，动态获得涡粘模型的系数；并展开亚格子应力的各项同性部分，基于亚格子动能与亚格子应力的各项同性部分的关系，得到能流关系式中的未知系数；
7.步骤3、计算得到动态得到亚格子热流以及亚格子组分通量项的系数；
8.步骤4、基于无限展开将亚格子动能输运方程中的未封闭项进行建模，使得整个方程组封闭。
9.有益效果：
10.本发明的方法，通过附加的亚格子动能方程，可以准确预测亚格子动能。然后，利用亚格子动能和能流的双重约束，可以准确地确定亚格子涡粘模型。采用与亚格子应力展开类似的方法，待求解方程中的其他未闭合量可以很好地单独建模。该方法在不同的算例中进行测试，可以准确预测转捩、湍流混合等过程，取得了良好的模拟效果，同时也证明了该方法具有尺度自适应性。本发明提出的新模型不需要二次滤波即可动态求得模型系数，具有很好的网格自适应性以及时间历史效应，方便应用于复杂的工程计算当中。
附图说明
11.图1为本发明的方法流程图；
12.图2为槽道计算域示意图；
13.图3为van driest变换后得到的速度剖面；
14.图4为无量纲化的雷诺偏应力；
15.图5为无量纲化的湍流热通量；
16.图6为平板计算域示意图；
17.图7为不同网格设置下的速度剖面以及摩擦阻力系数。a是les-grida的速度剖面，b是les-grida摩擦阻力系数，c是les-gridb的速度剖面，d是les-gridb的摩擦阻力系数，e是les-gridc的速度剖面，f是les-gridc的摩擦阻力系数；
18.图8为球形汇聚的rm不稳定性的计算域示意图；
19.图9为混合层的内外半径随时间的变化(r1为内半径、r2为外半径)。
具体实施方式
20.下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整的描述，显然，所描述的实施例仅为本发明的一部分实施例，而不是全部的实施例，基于本发明中的实施例，本领域的普通技术人员在不付出创造性劳动的前提下所获得的所有其他实施例，都属于本发明的保护范围。
21.根据本发明的实施例，提出了一种准动态的亚格子一方程模型的大涡模拟方法，从可压缩的方程出发，推导了一种适用于可压缩流动的大涡模拟模型，即准动态的亚格子动能一方程模型，基于该模型进行大涡模拟。该模型使用亚格子动能以及能流的双约束来构建亚格子涡粘、亚格子热流以及亚格子扩散项，使得可以在不使用二次滤波的情况下动态得到模型系数，使得梯度模型和涡粘模型相结合，既可以得到较高的相关性，又具有很好的稳定性。
22.如图1所示，本发明的一种基于准动态的亚格子动能方程模型的大涡模拟方法，具体包括如下步骤：
23.步骤1、首先推导了亚格子动能的输运方程，并使用无限展开关系式对能流建模，得到能流关系式；
24.步骤2、将传统涡粘模型代入能流关系式后，得到涡粘模型所计算得到的能流，使涡粘模型计算得到的能流与建模得到的能流的真实值相等，动态获得涡粘模型的系数；并展开亚格子应力的各项同性部分，基于亚格子动能与亚格子应力的各项同性部分的关系，可以得到能流关系式中的未知系数；
25.步骤3、基于同样的方法，可以得到动态得到亚格子热流以及亚格子组分通量项的系数；
26.步骤4、基于无限展开将亚格子动能输运方程中的未封闭项进行建模，使得滤波后的navier-stokes与亚格子动能输运方程封闭。
27.根据本发明的实施例，具体推导过程如下：
28.在可压缩流动中，亚格子动能定义如下：
[0029][0030]
式中，
“‑”
表示滤波，“～”表示favre滤波。ρ是密度，ksgs是亚格子动能，ui是速度。
[0031]
推导得到亚格子动能的输运方程，并基于输运方程得到能流模型的系数；
[0032]
本发明的“准动态的亚格子动能一方程模型”包括：csm的计算表达式，亚格子普朗特数pr
sgs
的计算表达式公式，以及亚格子schmidt数的计算表达式；
[0033][0034]
其中：
[0035][0036][0037]
其中，当i＝j时，δ
ij
＝1，当i不等于j时，δ
ij
＝0；
[0038][0039][0040][0041][0042][0043]
是分子粘性，εs是螺旋耗散项，εd是膨胀耗散项，∏
p
是压力扩散项，jj是三阶关联项。τ
ij
是亚格子应力，是应变率张量，是分子粘性系数，p是压力，qj是亚格子热流。
[0044]
能流是反映湍流级串过程中的关键物理量，在准动态一方程方法中，首先对能流建模，能流需要由亚格子应力求出；对能流建模后，需要求解模型系数，其系数由ksgs求得，而ksgs由其输运方程求出，具体如下：
[0045]
考虑以下展开：
[0046][0047]
其中，f、g为某一物理量，也可以为向量、矢量等，g(x,y)为滤波器。
[0048]
对亚格子应力使用以上展开：
[0049][0050]
其中，c0为未知系数，
△k为滤波宽度。
[0051]
则可以得到能流关系式：
[0052][0053]
使用上述展开亚格子应力的各项同性部分：
[0054][0055]
基于亚格子动能与亚格子应力的各项同性部分的关系，可以得到：
[0056][0057]
这样可以得到未知系数c0，这样就形成了亚格子动能对未封闭项的约束。所述的未封闭项是对所有的亚格子未封闭项，本发明都采用无限级数展开，都会产生一个系数，假设所有系数都取c0。
[0058]
使上述得到的能流与smagorinsky模型得到的能流相等，则有：
[0059][0060]
其中：
[0061][0062][0063][0064]
∏
δsma
是smagorinsky模型各项异性部分，∏
δsmi
是各项同性部分；
[0065]
而∏
△
的各项异性部分和各项同性部分分别如下：
[0066][0067][0068]
使准动态一方程方法中的能流与smagorinsky模型的能流的各项异性部分相等：
[0069][0070]
可以得到smagorinsky模型的系数为：
[0071][0072]
由于亚格子动能是一个未封闭项(此处只是亚格子动能本身)，需要求解亚格子动能的输运方程求得，而其输运方程中存在未封闭项，对压力扩散项以及两个耗散项使用展开建模如下：
[0073][0074][0075][0076]
对三阶关联项，建模为
[0077]
对于可压缩navior-stokes方程中的亚格子热流项，同样使用c0对其进行约束，考虑建模形式如下：
[0078][0079]
本发明已经得到了μ
sgs
，接下来要得到亚格子普朗特数pr
sgs
。
[0080]
对亚格子热流进行展开可以得到：
[0081][0082]
使用以下关系：
[0083][0084]
可以得到：
[0085][0086]
在湍流混合问题中，需要求解组分输运方程：
[0087][0088]
其中亚格子组分通量项：
[0089][0090]
该项可以采用以下方式建模：
[0091][0092]
sc
sgs,k
为亚格子schmidt数，是一个未知的常数。采用与求解亚格子普朗特数相同的方法来求解亚格子schmidt数，可以得到：
[0093][0094]
接下来对新模型做算例验证，该模型称为准动态亚格子动能一方程模型(qkm)即包括前述的求解c
sm
,pr
sgs
以及sc
sgs,k
的公式。
[0095]
将该方法应用于大涡模拟的流程：
[0096]
对某个计算算例，选择合适的大涡模拟的网格，求解滤波后的navior-stokes方程，滤波后的n-s方程中存在未封闭项，将上述模型求解亚格子应力、亚格子热流以及亚格子组分通量项的方法代入，附加亚格子动能输运方程以求解模型系数，之后进行时间推进，得到流场结果。该准动态方法可以在不需要二次滤波的情况下得到模型系数，可应用于复杂边界的问题，并且该方法已经被证明可以很好的预测转捩、湍流等过程，相较于传统的模型有一定的优势。
[0097]
根据本发明的一个实施例，以可压缩槽道为例，对本发明的方法进行说明。
[0098]
首先在可压缩槽道中进行测试，槽道计算域示意图如图2所示，计算网格设置与流动参数如表1所示。计算的来流马赫数为1.5，雷诺数为3000。使用直接数值模拟(dns)、动态的smagorinsky模型(dsm)与动态的一方程模型(dk-equation)做对比。
[0099]
表1网格设置及主要参数
[0100] 网格
△
x
+
△ymin+
△z+
dns900
×
201
×
3002.990.322.99dsm48
×
65
×
4857.551.0719.18dk-equation48
×
65
×
4857.881.0619.20qkm48
×
65
×
4857.451.0719.18
[0101]
图3-图5展示的槽道中的关键物理量的对比结果。可以看出，新模型的结果要与dns更为接近，且明显好于其他对比模型。
[0102]
根据本发明的又一个实施例，以可压缩平板边界层为例，对本发明的方法进行说明。
[0103]
本算例为空间发展的平板，包括层流、转捩、湍流部分。图6是平板计算域示意图。表2为网格设置，大涡模拟计算共有密-中-疏三套设置，来检验模型的网格适应性。计算的来流马赫数为2.25，雷诺数为635000。
[0104]
表2可压缩平板网格设置
[0105] 网格
△
x
+
△ymin+
△z+
dns10000
×
90
×
3206.00.585.47les-grida1500
×
90
×
10040.10.5817.5les-gridb1000
×
90
×
8060.20.5821.9les-gridc1000
×
60
×
5060.21.0035.1
[0106]
图7不同网格设置下的速度剖面以及摩擦阻力系数。a和b是les-grida的速度剖面以及摩擦阻力系数，c和d是les-gridb的速度剖面以及摩擦阻力系数，e和f是les-gridc的速度剖面以及摩擦阻力系数。
[0107]
从图7展示的结果可以看出，新模型不仅可以很好的预测湍流部分，还可以很好的预测转捩峰以及转捩位置，且即便在网格比较疏的情况下，新模型依旧可以得到很好的结果，说明模型有很好的网格自适应性。
[0108]
根据本发明的又一个实施例，以球形汇聚的rm不稳定性为例，对本发明的方法进行说明。
[0109]
接下来的算例是球形汇聚的rm不稳定性，该算例是一个时间发展的算例，这点与
上述两个算例不同，网格设置见表3，计算域示意图见图8。马赫数约为1.5，atwood数约为0.578。传统的smagorinsky模型(sm)作为对比模型。
[0110]
表3球形汇聚的rm不稳定性的网格设置
[0111]
算例网格dns20483qkm3843sm3843[0112]
从图9可以看出，新模型可以很好的预测混合层内外半径的变化，预测结果好于传统的smagorinsky模型，说明其具有很好的时间历史效应。
[0113]
综上，本发明设计的模型不需要二次滤波即可动态求得模型系数，具有很好的网格自适应性以及时间历史效应，基于上述模型，本发明的大涡模拟方法可以方便应用于复杂的工程计算当中，比如高超声速升力体、高超声速压缩折角等算例。
[0114]
尽管上面对本发明说明性的具体实施方式进行了描述，以便于本技术领域的技术人员理解本发明，且应该清楚，本发明不限于具体实施方式的范围，对本技术领域的普通技术人员来讲，只要各种变化在所附的权利要求限定和确定的本发明的精神和范围内，这些变化是显而易见的，一切利用本发明构思的发明创造均在保护之列。