一种液态食品超声波加工过程中空化强度的表征算法

1.本发明属于食品加工技术领域，具体涉及一种液态食品超声波加工过程中空化强度的表征算法。


背景技术：

2.超声按频率可分为低频(功率)超声(20-100khz)(lfus)、高频(100khz-1mhz)超声(hfus)和诊断超声(1 500mhz)，众所周知，低频超声(如20khz)产生强大的物理效应，如介质中的高速液体喷射、高温、高压、冲击波、湍流和极端物理剪切力，而高频超声(200khz-800khz)通过声空化产生高产量的自由基，这些物理化学效应越来越多被用于食品加工过程中，因此超声波作为一种新型的绿色技术，在食品工业中显示出巨大的潜力，尤其是液态食品加工领域，如超声提取，超声乳化，超声辅助吸附，超声波灭菌等，目前描述超声空化强度方法主要有两类，第一是用驱动声压描述空化强度，此种方法只有出现空化现象后的声强分布才能粗略的反映空化强度，具有一定局限性，第二类是利用空化效应来描述，液体食品加工过程中常用量热法来测定超声空化强度，单位是w/l或w/ml，更多的用纯数(w)，但是超声热效应并不能全部代表空化效应，仍具有一定局限性，因为空化是一个复杂的过程，是许多物理、化学过程的综合现象，它的强弱本身就需要多个物理量来共同描述，到目前为止，超声波输入的能量，尤其是超声空化强度很难去表征，因此，限制了超声波技术在液态食品加工中的应用。
3.针对于上述问题，本发明通过解析液态食品中超声空化气泡的成长过程，明确空泡内自由基反应的温度、压力，进而对空泡内自由基反应过程进行计算，得出自由基反应底物和产物摩尔量的变化，在此基础上对空化云中空泡数做出了计算，最终基于单个空泡的能量、空泡数量、超声加工时间和液态食品的处理体积，提出以累积空泡强度来表征空化强度的方法，该方法可以相对准确的描述超声空化强度。


技术实现要素：

4.本发明的目的是：旨在提供一种液态食品超声波加工过程中空化强度的表征算法，能够更加准确的描述超声空化强度，建立空化特征与液态超声食品加工特征的定量关系。
5.为实现上述技术目的，本发明采用的技术方案如下：
6.具体包括以下步骤：
7.步骤一：计算空化气泡的成长过程；
8.步骤二：计算空化气泡内的温度和压力；
9.步骤三：对空化气泡内气体的自由基反应动力学进行计算；
10.步骤四：对超声场下液态食品中h2o2浓度生成速率进行测定；
11.步骤五：对空化气泡数量进行推算；
12.步骤六：根据单空泡的能力、空化云中空泡数量、超声时间、液态食品处理量，建立
累计空化强度。
13.所述步骤一中，具体采用凯勒-米克西斯模型，简述为keller-miksis方程，其定量描述了具有可压缩性和粘性的液态食品中球形空化气泡径向动力学，其中空泡动力学可以采用如下公式表示：
[0014][0015][0016][0017]
其中，t为时间，单位为分钟或微秒；r为空泡半径，单位为μm；r0初始空泡半径，单位为μm；pv为空化泡内水蒸汽分压，其中25℃时为3.17
×
103pa；c为液态食品中声速，数值为1500m s-1
；ρw为水的密度，数值为998kg m-3
；ρ为液体食品的密度，数值为kg m-3
；p
stat
为环境静压，单位为pa；ia为液态食品中的声强，单位为w m-2
；p1为泡液界面液体侧压力与环境压差，单位为pa；pa为与声强相关的驱动压力，单位为pa，σ为液态食品的表面张力，单位为n m-1
；μ为液态食品的粘度，单位为n s m-2
；γ泡内气体的多方指数，其中水蒸气为1.33，氧气为1.4。
[0018]
最后利用四阶龙格-库塔法在软件matlab中数值求解keller-miksis方程。
[0019]
所述步骤二中，在压缩过程中，若空化气泡的半径r达到范德瓦尔斯硬核半径的阈值r0/8.54时，则认定为空化气泡崩塌，此时根据绝热定律，绝热阶段的空化气泡内的温度k和压力pa则可表示为：
[0020][0021][0022]
其中p
bubble
为空泡内压力pa，k为空泡内物质的数量，t
bubble
为气泡内温度k。
[0023]
所述步骤三中，反应的计算始于绝热阶段的开始，此时通过软件matlab求解含有氧气和水蒸气的空泡内化学反应，通过化学动力学模拟，计算出在任何温度下气泡内物质的物质量，其中气泡内物质包括o2、h2o、
·
oh、h
·
、o、ho2·
、h2和h2o2，且在化学反应动力学计算中，第三体反应物为o2，具体的计算步骤包括：
[0024]
步骤a，根据化学动力学理论给出含有k个自由基的可逆反应速率的表达式：
[0025][0026]
步骤b，通过下述公式计算步骤a中给定物质xk的生产速率：
[0027][0028][0029]
进一步的ri中k
fi
和k
ri
采用阿伦尼乌斯形式来表示：
[0030]
[0031][0032]
上述计算公式中，v
′
ki
为第i个反应的正化学计量系数；v
″
ki
为第i个反应的反化学计量系数；wk为第k个物质的关于时间的生产速率，单位为mol s-1
；xk为第k种物质的化学符号；[xk]为第k种物质的摩尔浓度，单位为moll-1
；ri为第i个反应中k物质的反应速率，单位为mol s-1
；k
fi
为第i个反应的正反应速率常数，其中两种底物反应的单位为cm
3 mol-1
s-1
，三种底物反应的单位为cm
6 mol-2
s-1
；k
ri
为第i个反应的逆反应速率常数，其中两种反应底物反应的单位为cm
3 mol-1
s-1
，三种物质的反应为cm
6 mol-2
s-1
；a
fi
和a
ri
分别为k
fi
和k
ri
的指前因子其中两种底物反应的单位为cm
3 mol-1
s-1
，三种底物反应的单位为cm
6 mol-2
s-1
；e
a,fi
为k
fi
中第i个反应中正反应活化能，单位为cal mol-1
；e
a,ri
为k
ri
中第i个反应中逆反应的活化能，单位为cal mol-1
。
[0033]
气泡内所有物质的生成速率以对应方程表示，然后将正反应速率常数和逆反应速率常数带入前述对应方程内，即可得到每种化学物质的具体反应速率表达式，当气泡达到最大尺寸r
max
时开始模拟自由基反应动力学，并在计算自由基之前，用溶氧仪测得25℃条件下已饱和液态食品溶解氧含量为8.15
±
0.60mg l-1
，对于25℃含饱和o2和水蒸气的空泡，气泡内的初始气体o2压力用如下公式表示：
[0034][0035]
再根据理想气体定律pv＝nrgt,，用如下公式表示空泡中o2和水蒸气的初始摩尔数：
[0036][0037][0038]
其中，为饱和o2/水蒸气空泡中氧气的初始压力pa；为空泡中氧气的初始摩尔数mol；为空泡中水蒸气的初始摩尔数mol；rg为通用气体常数8.314j mol-1
k-1
；v0为空泡的初始体积μm3；t0为空泡内的初始温度k。
[0039]
以o2作为第三体反应物的af或ar值需要通过乘以一个系数来修正化学反应，然后通过求解每种化学物质的具体反应速率表达式的方程，结合空泡温度、压力和半径分布，得出绝热相中所有化学反应物的物质量演化；当空泡破裂，对自由基的计算结束。
[0040]
所述步骤四中，采用weissier反应检测液态食品超声过程中h2o2浓度的生成速率。
[0041]
所述步骤五中，进一步基于单个空泡中产生的h2o2、
·
oh和ho2·
摩尔数和液态食品中h2o2生成速率，计算空化云中空泡数：
[0042][0043]
其中，n
bubble
为单位时间内单位体积内液态食品体系内坍塌的空泡数l-1
s-1
；为空泡中h2o2的摩尔产率mol；r(h2o2)为h2o2的生成速率mol l-1
s-1
；n
·
oh
为空泡中
·
oh的摩尔产率mol；为空泡中ho2·
的摩尔产率mol。
[0044]
所述步骤六中，为了建立空化特性与超声食品加工特性的定量关系，我们引入了一个表征超声空化强度的参数，基于单空泡的能力、空化云中空泡数量、超声时间、液态食品处理量，建立累计空化强度，即气泡的累积崩塌压力ccp，其表达式为：
[0045]
ccp＝n
bubble
×
p
collpase
×
t
×
v；
[0046]
其中，t为超声加工时间min，v为液态食品的体积l。
[0047]
本发明相较于现有技术至少具有以下优点：
[0048]
通过将空泡数、空泡坍塌压力、液体处理体积和超声加工时间相乘，能够相对准确的表征超声空化强度这个物理量；通过建立空化特性与液态超声食品加工特性的定量关系，有利于液态食品超声加工装备的设计和超声参数的优化。
附图说明
[0049]
本发明可以通过附图给出的非限定性实施例进一步说明。
[0050]
图1为本发明空化气泡中自由基的演变过程示意图。
[0051]
图2为本发明豆乳超声加工过程中h2o2浓度随时间的变化示意图。
[0052]
图3为超声辅助双水相萃取花色苷过程中，花色苷提取率随累积崩塌压力的变化示意图。
[0053]
图4为超声乳化o/w纳米乳液过程中累积空泡强度与乳状液颗粒大小的关系示意图。
[0054]
图5为超声波处理豆浆过程中脂肪氧化酶残留活性随累积崩塌压力的变化示意图。
[0055]
图6为超声破碎酵母细胞过程中，酵母粒径随累积崩塌压力的变化示意图。
[0056]
图7为本发明中坍塌的含有o2/水蒸气的空化气泡中发生的化学反应类型示意图。
[0057]
图8为本发明中饱和的含有o2/水蒸气的空泡内每种物质的产生速率示意图。
[0058]
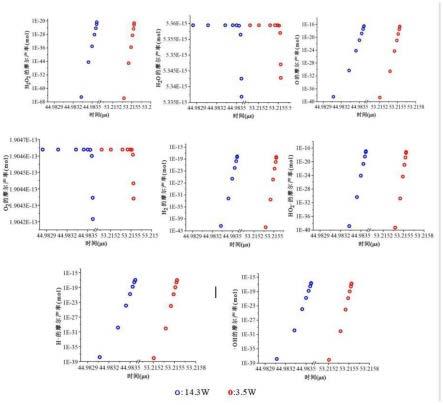
图9为将图7中正向和逆向反应速率常数带入图8方程后的含有饱和的o2/水蒸气空泡内每种物质的产生速率第一部分示意图。
[0059]
图10为将图7中正向和逆向反应速率常数带入图8方程后的含有饱和的o2/水蒸气空泡内每种物质的产生速率第二部分示意图。
[0060]
图11为将图7中正向和逆向反应速率常数带入图8方程后的含有饱和的o2/水蒸气空泡内每种物质的产生速率第三部分示意图。
具体实施方式
[0061]
为了使本领域的技术人员可以更好地理解本发明，下面结合附图和实施例对本发明技术方案进一步说明。
[0062]
本实施例是一种超声波食品加工过程中超声强度的表征算法，其包括如下步骤：
[0063]
步骤一：
[0064]
采用keller-miksis方程定量描述了具有可压缩性和粘性的液态食品中球形空化气泡径向动力学，可用以下动力学公式表示：
[0065]
[0066][0067][0068]
其中，t为时间，单位为分钟或微秒；r为空泡半径，单位为μm；r0初始空泡半径，单位为μm；pv为空化泡内水蒸汽分压，其中25℃时为3.17
×
103pa；c为液态食品中声速，数值为1500m s-1
；ρw为水的密度，数值为998kg m-3
；ρ为液体食品的密度，数值为kg m-3
；p
stat
为环境静压，单位为pa；ia为液态食品中的声强，单位为w m-2
；p1为泡液界面液体侧压力与环境压差，单位为pa；pa为与声强相关的驱动压力，单位为pa，σ为液态食品的表面张力，单位为n m-1
；μ为液态食品的粘度，单位为n s m-2
；γ泡内气体的多方指数，其中水蒸气为1.33，氧气为1.4。
[0069]
再利用四阶龙格-库塔法在matlab中数值求解keller-miksis方程。
[0070]
步骤二，
[0071]
所述步骤二中，在压缩过程中，若空化气泡的半径r达到范德瓦尔斯硬核半径的阈值r0/8.54时，则认定为空化气泡崩塌，此时根据绝热定律，绝热阶段的空化气泡内的温度k和压力pa则可表示为：
[0072][0073][0074]
其中p
bubble
为空泡内压力pa，k为空泡内物质的数量，t
bubble
为气泡内温度k，当空泡达到范德华硬核半径时，空泡内部温度为3908k，压力为1.820
×
109pa。
[0075]
步骤三：
[0076]
通过软件matlab求解图7中所示的初始含有氧气和水蒸气的空泡内化学反应，通过化学动力学模拟，计算出在任何温度下气泡内所有物质如o2、h2o、
·
oh、h
·
、o、ho2·
、h2和h2o2的物质的量，其中化学反应动力学计算中第三体反应物为o2，单个o2/水蒸气空泡动态寿命过程中化学物质摩尔产率的变化如图1所示，它们为估计空化云中的空泡数量提供了基础；具体计算步骤如下:
[0077]
步骤a，首先根据化学动力学理论给出含有k个自由基的可逆反应速率的表达式：
[0078][0079]
步骤b，然后通过下述公式计算步骤a中给定物质xk的生产速率：
[0080][0081][0082]
进一步的ri中k
fi
和k
ri
采用阿伦尼乌斯形式来表示：
[0083][0084]
[0085]
上述计算公式中，v
′
ki
为第i个反应的正化学计量系数；v
″
ki
为第i个反应的反化学计量系数；wk为第k个物质的关于时间的生产速率，单位为mol s-1
；xk为第k种物质的化学符号；[xk]为第k种物质的摩尔浓度，单位为moll-1
；ri为第i个反应中k物质的反应速率，单位为mol s-1
；k
fi
为第i个反应的正反应速率常数，其中两种底物反应的单位为cm
3 mol-1
s-1
，三种底物反应的单位为cm
6 mol-2
s-1
；k
ri
为第i个反应的逆反应速率常数，其中两种反应底物反应的单位为cm
3 mol-1
s-1
，三种物质的反应为cm
6 mol-2
s-1
；a
fi
和a
ri
分别为k
fi
和k
ri
的指前因子其中两种底物反应的单位为cm
3 mol-1
s-1
，三种底物反应的单位为cm
6 mol-2
s-1
；e
a,fi
为k
fi
中第i个反应中正反应活化能，单位为cal mol-1
；e
a,ri
为k
ri
中第i个反应中逆反应的活化能，单位为cal mol-1
。
[0086]
图7所列的所有物质的生成速率以图8中的方程表示，然后将正反应速率常数和逆反应速率常数代入图8中的方程，可得到图9-图11中对每种化学物质的具体反应速率表达式；当气泡达到最大尺寸r
max
时开始模拟自由基反应动力学，并在计算自由基之前，用溶氧仪测得25℃条件下已饱和液态食品溶解氧含量为8.15
±
0.60mg l-1
，对于25℃含饱和o2和水蒸气的空泡，气泡内的初始气体o2压力用如下公式表示：
[0087][0088]
再根据理想气体定律pv＝nrgt,，用如下公式表示空泡中o2和水蒸气的初始摩尔数：
[0089][0090][0091]
其中，为饱和o2/水蒸气空泡中氧气的初始压力pa；为空泡中氧气的初始摩尔数mol；为空泡中水蒸气的初始摩尔数mol；rg为通用气体常数8.314j mol-1
k-1
；v0为空泡的初始体积μm3；t0为空泡内的初始温度k。
[0092]
以o2作为第三体反应物的af或ar值需要通过乘以一个系数来修正化学反应，然后通过求解每种化学物质的具体反应速率表达式的方程，结合空泡温度、压力和半径分布，得出绝热相中所有化学反应物的物质量演化；当空泡破裂，对自由基的计算结束。
[0093]
步骤四：
[0094]
采用weissier反应检测液态食品超声过程中h2o2浓度的生成速率，记录如图2所示的强超声预处理和温和超声吸附过程中h2o2浓度的变化，从图直线斜率即为h2o2的生成速率，用于下一步推测空化云中空泡数量。
[0095]
步骤五：
[0096]
所述步骤五中，进一步基于单个空泡中产生的h2o2、
·
oh和ho2·
摩尔数和液态食品中h2o2生成速率，计算空化云中空泡数：
[0097][0098]
其中，n
bubble
为单位时间内单位体积内液态食品体系内坍塌的空泡数l-1
s-1
；为空泡中h2o2的摩尔产率mol；r(h2o2)为h2o2的生成速率mol l-1
s-1
；n
·
oh
为空泡中
·
oh的摩
尔产率mol；为空泡中ho2·
的摩尔产率mol。
[0099]
步骤六：
[0100]
为了建立空化特性与超声食品加工特性的定量关系，我们引入了一个表征超声空化强度的参数，基于单空泡的能力、空化云中空泡数量、超声时间、液态食品处理量，建立累计空化强度，即气泡的累积崩塌压力ccp，其表达式为：
[0101]
ccp＝n
bubble
×
p
collpase
×
t
×
v；
[0102]
其中，t为超声加工时间min，v为液态食品的体积l。
[0103]
气泡的累积崩塌压力综合了空泡数、空泡坍塌压力、液体食品处理体积和超声时间四个物理量，因此ccp可以更好的表征液态介质中超声空化强度。
[0104]
本发明的内容可以应用到各种液态食品超声波加工过程中，建立起加工特性与累积崩塌压力之间的定量关系，如图3、图4、图5、图6所示，此种定量关系有利于液态食品超声加工装备的设计和超声参数的优化。
[0105]
上述实施例仅示例性说明本发明的原理及其功效，而非用于限制本发明。任何熟悉此技术的人士皆可在不违背本发明的精神及范畴下，对上述实施例进行修饰或改变。因此，凡所属技术领域中具有通常知识者在未脱离本发明所揭示的精神与技术思想下所完成的一切等效修饰或改变，仍应由本发明的权利要求所涵盖。