基于顶点重要度的二次误差度量边折叠BIM轻量化方法

基于顶点重要度的二次误差度量边折叠bim轻量化方法
技术领域
1.本发明涉及图像重构领域，尤其涉及一种基于顶点重要度的二次误差度量边折叠bim轻量化方法。


背景技术：

2.bim(建筑信息模型)由专业的建模软件建立，模型集成了建筑物的全部工程信息或数据，使之应用与工程项目的不同阶段，达到工程信息灵活共享与传递的目的。伴随着互联网的发展，越来越多的bim用户希望在web端直接浏览三维模型。
3.传统的bim应用程序都基于桌面客户端，且需要较高的计算机配置：高频cpu、大内存、独立显卡。在从桌面端走向web端、移动端的过程中，由于受浏览器计算能力和内存限制等方面的影响，基于桌面的对模型的数据组织和消费方式必须做出相应调整，即需要更多的使用三维模型轻量化技术对模型进行深度处理。
4.目前主流的轻量化方法包含数模分离和三维几何数据轻量化处理这两方面。bim模型包含三维几何数据和模型结构属性等非几何数据两部分。
5.首先，webgl轻量化bim引擎需要将几何数据和非几何数据进行拆分。通过这样的处理，原始bim模型文件中约20％-50％的非几何数据会被剥离出去，输出为数据文件供bim应用开发使用。剥离非几何数据后剩下的三维几何数据，需要进一步轻量化处理优化，以降低三维几何数据量，节约客户端电脑的渲染计算量，从而提高bim模型下载、渲染和功能处理的速度。三维几何数据优化这块，一般采取的方案包括：通过采用参数化或三角化的描述手段来降低三维几何数据的数据文件大小；相似性算法减少构件存储量；构建符合场景远近原则的多级构件组织体系。
6.现有的轻量化方法为实现模型在web端、移动端的快速传递和加载，主要通过模型减面、数据分离等方法来减少bim模型的模型文件大小。
7.目前常用的网格简化算法如体积平方和度量算法、二次误差度量算法等单指标算法，容易形成误差积累，且大多没有考虑网格模型的细节特征，忽略网格质量和边界的影响，在简化模型的同时容易丢失模型的几何特征，高简化率下模型过于平滑。类曲率特征度算法和能量函数算法等多指标算法引入了描述网格特征的参数，但其大多参数需要根据经验设定，对于尖锐特征和平坦区域组成的模型进行简化时效果并不明显。


技术实现要素：

8.针对以上问题，本发明提供一种基于顶点重要度的二次误差度量边折叠bim轻量化方法，包括以下步骤：
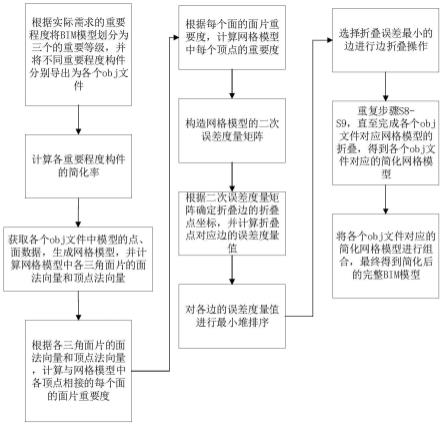
9.s1、根据实际需求的重要程度将bim模型划分为三个的重要等级，并将不同重要程度构件分别导出为各个obj文件；
10.s2、计算各重要程度构件的简化率；
11.s3、获取各个obj文件中模型的点、面数据，生成网格模型，并计算网格模型中各三
角面片的面法向量和顶点法向量；
12.s4、根据各三角面片的面法向量和顶点法向量，计算与网格模型中各顶点相接的每个面的面片重要度；
13.s5、根据每个面的面片重要度，计算网格模型中每个顶点的重要度；
14.s6、构造网格模型的二次误差度量矩阵；
15.s7、根据二次误差度量矩阵确定折叠边的折叠点坐标，并计算折叠点对应边的误差度量值；
16.s8、对各边的误差度量值进行最小堆排序；
17.s9、选择折叠误差最小的边进行边折叠操作；
18.s10、重复步骤s8-s9，直至完成各个obj文件对应网格模型的折叠，得到各个obj文件对应的简化网格模型；
19.s11、将各个obj文件对应的简化网格模型进行组合，最终得到简化后的完整bim模型。
20.本发明提供的有益效果是：
21.1、对bim几何模型使用基于二次误差度量的边折叠算法进行三维网格简化,得到满足简化要求的三维几何模型，能够有效改善bim模型的存储和传输问题。
22.2、考虑三维模型尤其是三维建筑模型在三角网格中的过简化问题，在二次误差度量的基础上引入了顶点重要度与模型特征因子作为约束因子，使建筑模型既保证简化模型同初始模型在几何上尽可能相似，又能较好地保留初始模型的各部分特征。
附图说明
23.图1是本发明方法流程示意图；
24.图2是边折叠原理示意图；
25.图3(a)为简化前厂房网格模型，(b)为简化后厂房网格模型。
26.图4(a)为简化前的厂房内部设备的网格和模型，(b)为采用本方法简化后厂房内部设备的网格和模型。(c)为采用不考虑顶点重要度的二次误差度量边折叠算法进行简化的厂房内部设备的网格和模型。
具体实施方式
27.为使本发明的目的、技术方案和优点更加清楚，下面将结合附图对本发明实施方式作进一步地描述。
28.s1、根据实际需求的重要程度将bim模型划分为三个的重要等级，并将不同重要程度构件分别导出为各个obj文件；
29.需要说明的是，针对bim模型中不同构件在其实际应用中的需求程度分为若干等级，一般设为三级，当然，也可以根据模型在实际应用中的不同需求来划分。将划分好的不同重要度构件分别导出为obj文件格式。
30.本技术中将其划分为3级；
31.s2、计算各重要程度构件的简化率；
32.需要说明的是，对于设定的总简化率p，由下列公式计算不同重要等级的部件所需
的简化率:
[0033][0034]
式中pⅰ、pⅱ、pⅲ为三个等级构件的简化率，nⅰ、nⅲ为三个等级构件模型的面数。一般二级构件简化率pⅱ与设定简化率p相等，三级构件简化率pⅲ一般比设定简化率p高0.2～0.3。
[0035]
s3、获取各个obj文件中模型的点、面数据，生成网格模型，并计算网格模型中各三角面片的面法向量和顶点法向量；
[0036]
需要说明的是，为获取模型特征信息，输入步骤一导出的obj模型文件，读取模型的点、面数据，生成网格。计算网格模型各个三角面片的面法向量和顶点法向量：
[0037][0038]
式中表示面片的平面法向量，ai、bi、ci、di为直接读取得到的模型面片信息，ai,bi,ci,di为标准化后的模型面片信息。
[0039][0040]
式中表示网格顶点v的顶点法向量，n为与顶点v相接的三角面片个数。顶点法向量即计算与该顶点相接的所有面片的面片法向量的算术平均值。
[0041]
s4、根据各三角面片的面法向量和顶点法向量，计算与网格模型中各顶点相接的每个面的面片重要度；
[0042]
需要说明的是，为区分不同面片的重要程度，引入面片重要度描述网格模型中的面片特征，计算模型中与顶点相接的每个面的面片重要度：
[0043][0044]
式中，φ为面片重要度，通过计算面片的平缓程度表示模型特征。β为面片法向量与顶点法向量夹角，两者都能表示三角面片在顶点附近的尖锐程度。为顶点法向量和面法向量。
[0045]
s5、根据每个面的面片重要度，计算网格模型中每个顶点的重要度；
[0046]
需要说明的是，本技术引入表征模型顶点尖锐程度的顶点重要度以控制三维网格模型整体特征，按下式计算模型中每个顶点的顶点重要度：
[0047][0048]
式中，λ为顶点重要度，ceiling为向上取整函数，n为与顶点相连面片个数，k为模
型特征因子，取值范围为0到1，由使用者根据模型的特征指定。
[0049]
s6、构造网格模型的二次误差度量矩阵；
[0050]
需要说明的是，本技术采用二次误差度量即折叠顶点到原相邻面片距离的平方和，描述被折叠后产生新的面与未折叠前的差异：
[0051][0052]
式中，为顶点vi对应的二次误差度量矩阵，网格顶点到其所有相关联三角形的集合记为planes(v)，pk＝(a,b,c,d)
t
表示planes(v)中每个三角面片所在的标准化平面方程，记为：ax+by+cz+d＝0,n为顶点vi相接的三角面片个数。
[0053]
边(v1,v2)折叠到点v0的过程如图1所示，将步骤五得到的顶点重要度λ作为权重因子引入二次误差度量，得到边(v1,v2)的折叠点v0误差度量矩阵：
[0054][0055]
s7、根据二次误差度量矩阵确定折叠边的折叠点坐标，并计算折叠点对应边的误差度量值；
[0056]
需要说明的是，折叠点的二次误差度量值误差度量值按下式计算：
[0057][0058]
式中，δ(v0)为折叠点v0的误差度量值，即边(v1,v2)的误差度量值，v
x
,vy,vz为v0的三维坐标，为步骤六计算得的折叠点v0的二次误差度量矩阵。
[0059]
折叠点v0的位置要使边折叠后的模型与原模型的差异最小，即误差度量值要最小。
[0060]
式(8)为二次型，令其一阶导数为0，使δ(v0)的值最小，得到下列矩阵求解满足要求的折叠点v0坐标。
[0061][0062]
上述矩阵中q
ij
为矩阵对应的元素。若上列矩阵不可逆，v0便取v1、v2和改边中点中使得误差度量值最小的点。
[0063]
确定v0坐标后，每条边的误差度量值δ(v0)即可通过式(8)求得。
[0064]
s8、对各边的误差度量值进行最小堆排序；
[0065]
需要说明的是，最小堆排序的流程描述如下：将所有边的δ(v0)值构造成一个最小堆，使其任一非终端节点的数据值均不大于其左子节点和右子节点的值。此时，整个序列的最小值就是堆顶的根节点。将其与堆数组的末尾元素交换，此时末尾元素就是最小值，然后将剩余的n-1个序列重新构造成一个堆，这样就会得到n个元素中的次最小值。如此反复
执行，得到一个有序序列。这个过程其实实质为：先构建一个最小二叉堆，然后不停的取出最小元素插入到新的队列中，以此达到排序的目的。
[0066]
s9、选择折叠误差最小的边进行边折叠操作；
[0067]
需要说明的是，为了在最大限度保留模型特征的基础上减少模型面数，选择折叠误差最小的边进行边折叠操作。
[0068]
请参考图2，图2是边折叠原理示意图；将所有与该边两段顶点相连的边都更新连接至新顶点处，删除所有退化的边与三角形，记录折叠后的网格模型面数n
′i。
[0069]
s10、重复步骤s8-s9，直至完成各个obj文件对应网格模型的折叠，得到各个obj文件对应的简化网格模型；
[0070]
需要说明的是，通过重复s8-s9，迭代网格使模型满足终止条件：
[0071]n′i≤piniꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(10)
[0072]
式中，ni为不同重要度构件对应的原始面数，pi为该重要度对应的简化率，n
′i为步骤五边折叠操作后的模型面数。
[0073]
s11、将各个obj文件对应的简化网格模型进行组合，最终得到简化后的完整bim模型。
[0074]
需要说明的是，在建模软件中组合三组不同重要度的简化模型，得到简化后的完整模型文件。
[0075]
本发明实例采用的模型是某水库厂房bim模型，如图3(a)所示，该bim模型由127个构件组成，有133957个顶点，262343个面，模型文件大小124mb。现针对其运营维护应用需求，对该模型进行简化，总简化率取0.5。
[0076]
基于顶点重要度的二次误差度量边折叠bim轻量化过程如下：
[0077]
1)模型预处理：模型中的一些机电设备建模复杂，使用简化模型代替。采用简化模型和细节贴图的形式进行原位替换，使用贴图来表现原构件的表面细节。将配电箱、控制台等复杂几何形体构件以及门、窗等低重要度构件可用简易模型替换，再用贴图来展现模型表面的细节。
[0078]
2)模型构件重要度分级：针对bim模型实际应用需求，对该厂房模型构件重要度进行分级。使用建模软件读取模型，获取模型构件列表。根据运维需求，对构件进行分级。厂房的水轮机、配电柜等机电设备为一级重要度；厂房的梁、柱、墙等建筑结构构件为二级重要度；厂房内的其他装饰建模如卫生间、办公室内的构件为三级重要度。将三组不同重要度构件分别导出用于之后的三角网格简化。
[0079]
经过计算得三组构建的简化率分别为0.34，0.5，0.75。
[0080]
3)三角网格简化：根据模型构件重要度分级设置的简化率分别对三组部件进行简化。由基于顶点重要度的二次误差度量边折叠算法得到简化后的三组模型构件，再次组合得到简化后的bim模型文件。简化后的模型如图3(b)所示，顶点数60593，面数120236，模型文件大小5.13mb。由图4(a)到图4(b)的变化可看出，模型在较高简化率下仍然保持较好的细节特征和外部轮廓。而图4(c)由于没有考虑顶点重要度，在高化率下发生了过简化，出现了局部面片破裂的现象。
[0081]
本发明的有益效果是：
[0082]
1、对bim几何模型使用基于二次误差度量的边折叠算法进行三维网格简化,得到
满足简化要求的三维几何模型，能够有效改善bim模型的存储和传输问题。
[0083]
2、考虑三维模型尤其是三维建筑模型在三角网格中的过简化问题，在二次误差度量的基础上引入了顶点重要度与模型特征因子作为约束因子，使建筑模型既保证简化模型同初始模型在几何上尽可能相似，又能较好地保留初始模型的各部分特征。
[0084]
以上所述仅为本发明的较佳实施例，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。