基于多元线性回归的设备能耗预测方法及装置与流程

1.本技术涉及酒店能耗监控技术领域，具体涉及一种基于多元线性回归的设备能耗预测方法及装置。


背景技术：

2.酒店房间的能源消耗主要用于空调、照明、电视、小家电等，与其它类型的能耗相比，酒店房间能耗具有自身的特点：如不同的酒店的用电设备种类不一，高端酒店房间数量多、面积大，采用中央空调，中央空调配有智能温控器，能监测房间的温度、风机的风速及时常等；中低端连锁酒店房间数量少、面积小，采用分体空调。房间的运行时间也不同，全年平均入住率的变化引起酒店内人员负荷的变化，如节假日、旅游黄金周等的入住率较高；室内环境及空调参数的选择因入住人员的要求而调节，因此随意性较大等等。以上诸多因素都会导致酒店客房的各服务设施具有不同的运营时间段，并由此产生其能量消耗的特殊性。
3.因此，如何对不同的用电设备的能耗进行预测，得到一个较为准确的能耗数据，再对此类数据进行数据分析，最终得出最有效的能耗节省措施成为了本领域亟需解决的问题。


技术实现要素：

4.为此，本技术提供一种基于多元线性回归的设备能耗预测方法及装置，以解决现有技术存在的如何对不同的用电设备的能耗进行预测，从而得出最有效的能耗节省措施的问题。
5.为了实现上述目的，本技术提供如下技术方案：
6.第一方面，一种基于多元线性回归的设备能耗预测方法，包括：
7.获取影响用电设备能耗的影响因素；
8.根据第一公式对影响因素进行标准化处理；
9.所述第一公式为：其中，其中，其中，为第j个指标的样本均值，sj为第j个指标的样本标准差，m为能耗影响因素的个数，即进行主成分分析的指标变量为m个，n为用电设备的个数，即共有n个评价对象，第i个评价对象的第j个指标变量的取值为x
ij
；
10.根据第二公式计算相关系数矩阵；
11.所述第二公式为：r＝(r
ij
)m×m，其中r
ii
＝1，r
ii
＝r
ij
，r
ij
是第i个指标与第j个指标的相关系数；
12.计算特征值和特征向量，根据所述特征向量得到m个第二指标变量；
13.所述第二指标变量为：
14.其中，y1是第一主成分，y2是第二主成分，y3是第三主成分，
…
，ym是第m主成分；
15.选择合适的主成分，计算综合得分，选取综合得分较高的变量作为主成分变量；
16.根据选取的综合得分较高的主成分变量建立多元线性回归方程；
17.检验所述多元线性回归方程的显著性；
18.取t值对应的最大概率值p
max
；
19.判断最大概率值p
max
是否小于等于临界值；
20.若小于等于临界值，则输出用电设备能耗与各个影响因素之间的多元线性回归方程。
21.进一步的，所述选择合适的主成分，计算综合得分，选取综合得分较高的变量作为主成分变量,具体为：
22.根据第三公式和第四公式计算特征值的信息贡献率和累计贡献率；
23.所述第三公式为：
24.所述第四公式为：
25.当α
p
接近于1时，选择前p个指标变量y1，y2，
…
，y
p
作为p个主成分，代替原来m个指标变量；
26.根据第五公式计算每个主成分的综合得分；
27.所述第五公式为：
28.将综合得分较高的变量作为主成分变量。
29.进一步的，所述α
p
为0.85、0.90或0.95。
30.进一步的，根据第五公式和第六公式计算所述多元线性回归方程的常数项和系数值；
31.所述第五公式为：
[0032][0033]
其中，
[0034][0035][0036]
所述第六公式为：
[0037]
进一步的，检验所述回归方程的显著性之前还包括：将总偏差平方和分解为回归平方和与残差平方和。
[0038]
进一步的，检验所述回归方程的显著性包括检验回归方程的显著性和检验偏回归系数的显著性。
[0039]
进一步的，检验所述回归方程的显著性时采用f分布进行检验。
[0040]
进一步的，检验偏回归系数时采用f分布和t分布进行检验。
[0041]
进一步的，所述临界值为0.05。
[0042]
第二方面，一种基于多元线性回归的设备能耗预测装置，包括：
[0043]
影响因素获取模块，用于获取影响用电设备能耗的影响因素；
[0044]
标准化模块，用于根据第一公式对影响因素进行标准化处理；
[0045]
所述第一公式为：其中，其中，其中，为第j个指标的样本均值，sj为第j个指标的样本标准差，m为能耗影响因素的个数，即进行主成分分析的指标变量为m个，n为用电设备的个数，即共有n个评价对象，第i个评价对象的第j个指标变量的取值为x
ij
；
[0046]
相关系数矩阵计算模块，用于根据第二公式计算相关系数矩阵；
[0047]
所述第二公式为：r＝(r
ij
)m×m，其中r
ii
＝1，r
ii
＝r
ij
，r
ij
是第i个指标与第j个指标的相关系数；
[0048]
特征值和特征向量计算模块，用于计算特征值和特征向量，根据所述特征向量得到m个第二指标变量；
[0049]
所述第二指标变量为：
[0050]
其中，y1是第一主成分，y2是第二主成分，y3是第三主成分，
…
，ym是第m主成分；
[0051]
主成分变量选取模块，用于选择合适的主成分，计算综合评价值，选取综合评价值较高的变量作为主成分变量；
[0052]
多元线性回归方程建立模块，用于根据选取的综合评价值较高主成分变量建立多
元线性回归方程；
[0053]
显著性检验模块，用于检验所述多元线性回归方程的显著性；
[0054]
概率值选取模块，用于选取t值对应的最大概率值p
max
；
[0055]
判断模块，用于判断最大概率值p
max
是否小于等于临界值；
[0056]
若小于等于临界值，则输出用电设备能耗与各个影响因素之间的多元线性回归方程。
[0057]
相比现有技术，本技术至少具有以下有益效果：
[0058]
本技术提供了一种基于多元线性回归的设备能耗预测方法及装置，通过主成分分析法将影响用电设备能耗的影响因素作为自变量，通过坐标的不断变换，将所有的相关变量作线性变换，转换为另一组不相关的变量，经过计算选取前几个贡献率较高的变量作为主成分，可以达到用较少的自变量来反应用电设备所用的能耗，以及避免自变量之间的多重共线性问题的目的。根据主成分分析法得出的主成分变量来建立多元线性回归方程，运用多元线性回归方法预测各个用电设备的能耗。本技术通过对用电设备的能耗进行预测，对预测出的能耗数据进行分析，得到更加合理有效的减少能耗措施。
附图说明
[0059]
为了更直观地说明现有技术以及本技术，下面给出几个示例性的附图。应当理解，附图中所示的具体形状、构造，通常不应视为实现本技术时的限定条件；例如，本领域技术人员基于本技术揭示的技术构思和示例性的附图，有能力对某些单元(部件)的增/减/归属划分、具体形状、位置关系、连接方式、尺寸比例关系等容易作出常规的调整或进一步的优化。
[0060]
图1为本技术实施例一提供的一种基于多元线性回归的能耗预测方法整体流程图；
[0061]
图2为本技术实施例一提供的主成分分析流程图；
[0062]
图3为本技术实施例一提供的多元线性回归方程建立流程图；
[0063]
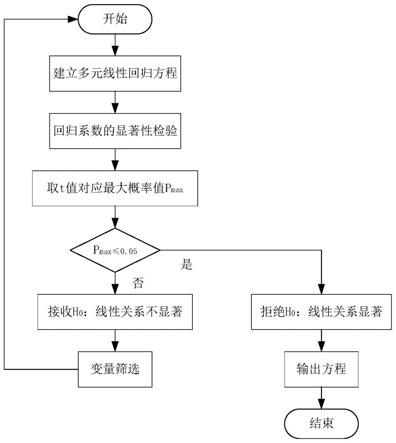
图4为本技术实施例一提供的回归方程检验流程图；
[0064]
图5为本技术实施例一提供的仿真运行流程图；
[0065]
图6为本技术实施例一提供的python运算流程图。
具体实施方式
[0066]
以下结合附图，通过具体实施例对本技术作进一步详述。
[0067]
在本技术的描述中：除非另有说明，“多个”的含义是两个或两个以上。本技术中的术语“第一”、“第二”、“第三”等旨在区别指代的对象，而不具有技术内涵方面的特别意义(例如，不应理解为对重要程度或次序等的强调)。“包括”、“包含”、“具有”等表述方式，同时还意味着“不限于”(某些单元、部件、材料、步骤等)。
[0068]
本技术中所引用的如“上”、“下”、“左”、“右”、“中间”等的用语，通常是为了便于对照附图直观理解，而并非对实际产品中位置关系的绝对限定。在未脱离本技术揭示的技术构思的情况下，这些相对位置关系的改变，当亦视为本技术表述的范畴。
[0069]
实施例一：
[0070]
请参阅图1，本实施例提供了一种基于多元线性回归的能耗预测方法，该方法主要由建立主成分分析的数学模型使用spss得到主成分、建立多元线性回归的数学模型得到预测结果二大模块组成。通过对多元线性回归数学模型进行运算，得到用电设备的具体能耗结果，通过与实际的能耗数据进行比较证明多元线性回归算法的可靠性，具体包括：
[0071]
s1：建立主成分分析的数学模型
[0072]
请参阅图2，主成分分析的数学模型将影响能耗的因素，如室外空气温度、房间空气温度、房间空气湿度、房间的保温性能、房间的面积、房间的朝向、房间的气流速度、通过门窗缝隙等损失的热量等进行贡献率的计算，得出主要的影响因素。
[0073]
s11：对原始数据进行标准化处理；
[0074]
具体的，假设对能耗的影响因素有m个，则进行主成分分析的指标变量为m个：x1,x2,...,xm。设用电设备为n个，即共有n个评价对象，第i个评价对象的第j个指标变量的取值为x
ij
。将各指标值x
ij
转换成标准化指标
[0075][0076][0077][0078]
其中，为第j个指标的样本均值，sj为第j个指标的样本标准差。
[0079]
s12：计算相关系数矩阵r；
[0080]
具体的，相关系数矩阵r＝(r
ij
)m×m[0081][0082]
其中，r
ii
＝1，r
ii
＝r
ij
，r
ij
是第i个指标与第j个指标的相关系数。
[0083]
s13：计算特征值和特征向量；
[0084]
具体的，指标变量的特征值需要由大到小排序，因此计算相关系数矩阵r的特征值λ1≥λ2≥...≥λm≥0，及对应的特征向量u1,u2,...,um,其中uj＝(u
1j
,u
2j
,
…
,u
nj
)
t
,由特征向量组成m个新的指标变量，如下列公式所示：
[0085][0086]
其中，y1是第一主成分，y2是第二主成分，y3是第三主成分，
…
，ym是第m主成分。
[0087]
s14：选择合适的主成分，计算综合评价值。
[0088]
s141：计算特征值的信息贡献率和累计贡献率；
[0089]
具体的，计算特征值λj(j＝1,2,...,m)的信息贡献率和累计贡献率，即主成分yj的
信息贡献率；
[0090][0091][0092]
其中，α
p
为主成分y1，y2，
…
，y
p
的累计贡献率，当α
p
接近于1(α
p
＝0.85,0.90,0.95)时，则选择前p个指标变量y1，y2，
…
，y
p
作为p个主成分，代替原来m个指标变量，从而可对p个主成分进行综合分析。
[0093]
s142：计算综合得分；
[0094]
具体的，综合得分：
[0095][0096]
其中，bj为第j个主成分的信息贡献率，根据综合得分值就可以进行评价。
[0097]
s2：建立多元线性回归的数学模型
[0098]
请参阅图3，本技术选用多元线性回归来对能耗进行预测，由于线性回归模型确定的是变量之间是相关关系，在大量的数据观察下，会表现出一定的规律性，可以借助函数关系式来表达。因此在建立多元线性回归模型时，需要对数学模型的输入数据进行标准化处理，明确数学模型中的输入变量，以及待测量。然后根据自变量与因变量的关系计算得到多元线性回归方程的表达式，再对多元线性回归模型进行显著性检验。具体分为以下几个步骤：
[0099]
s21：相关性分析；
[0100]
具体的，相关性分析是用来度量因变量与多个自变量之间的线性相关程度，即表示观察值y与估计值之间的相关程度。相关性一般由相关系数r来表示：
[0101][0102]
其中，r为决定系数。
[0103]
s22：建立回归方程；
[0104]
s221：假定线性回归方程的形式如下：
[0105]
y＝β0+β1x1+β2x2+
…
+βmxm+e
[0106]
上述公式表示数据中应变量y可以近似地表示为自变量x1,x2,...,xm的线性函数。其中β0为常数项，β1,β2,
…
,βm为偏回归系数，表示在其他自变量保持不变时，xj增加或减少一个单位时y的平均变化量，e是去除m个变量对y影响后的随机误差。
[0107]
s222：最小二乘法；
[0108][0109]
要使得的估计值最接近样本数据，也就是要和样本y的值最接近：
[0130][0131]
其中，0≤r2≤1，该系数越接近1，说明回归方程对数据的拟合程度越好。
[0132]
s234：f分布检验偏回归系数的显著性
[0133][0134]
df1＝1
[0135]
df2＝n-m-1
[0136]
其中，ss
回
(xj)表示偏回归平方和，其值越大说明相应的自变量越重要，只有m个自变量完全独立的情况下才会有：∑ss
回
(xj)＝ss
回
。
[0137]
s235：t分布检验偏回归系数的显著性
[0138][0139]
df＝n-m-1
[0140]
其中，bj为偏回归系数的估计值，是bj的标准差。
[0141]
s3：取t值对应的最大概率值p
max
；
[0142]
s4：判断是否p
max
≤0.05；
[0143]
若否，则接收h0：线性关系不显著，重新进行变量筛选；
[0144]
若是，则拒绝h0：线性关系不显著，输出线性回归方程。
[0145]
s5：结果表征；
[0146]
具体的，对中央空调的主要影响因素进行多元线性回归预测，程序运行完成后可以生成中央空调的具体能耗与各个影响因素的方程、中央空调能耗预测的百分点图、能耗预测拟合图等对中央空调的能耗情况进行表征。
[0147]
本技术通过主成分分析法将影响用电设备能耗的影响因素作为自变量，通过坐标的不断变换，将所有的相关变量作线性变换，转换为另一组不相关的变量，经过计算选取前几个贡献率较高的变量作为主成分，可以达到用较少的自变量来反应用电设备所用的能耗，以及避免自变量之间的多重共线性问题的目的。根据主成分分析法得出的主成分变量来建立多元线性回归方程，运用多元线性回归方法预测各个用电设备的能耗。通过对用电设备的能耗进行预测，对预测出的能耗数据进行分析，得到更加合理有效的减少能耗措施。
[0148]
实施例二：
[0149]
本实施例提供一种基于多元线性回归的设备能耗预测装置，包括：
[0150]
影响因素获取模块，用于获取影响用电设备能耗的影响因素；
[0151]
标准化模块，用于根据第一公式对影响因素进行标准化处理；
[0152]
所述第一公式为：其中，其中，其中，为第j个指标的样本均值，sj为第j个指标的样本
标准差，m为能耗影响因素的个数，即进行主成分分析的指标变量为m个，n为用电设备的个数，即共有n个评价对象，第i个评价对象的第j个指标变量的取值为x
ij
；
[0153]
相关系数矩阵计算模块，用于根据第二公式计算相关系数矩阵；
[0154]
所述第二公式为：r＝(r
ij
)m×m，其中r
ii
＝1，r
ii
＝r
ij
，r
ij
是第i个指标与第j个指标的相关系数；
[0155]
特征值和特征向量计算模块，用于计算特征值和特征向量，根据所述特征向量得到m个第二指标变量；
[0156]
所述第二指标变量为：
[0157]
其中，y1是第一主成分，y2是第二主成分，y3是第三主成分，
…
，ym是第m主成分；
[0158]
主成分变量选取模块，用于选择合适的主成分，计算综合评价值，选取综合评价值较高的变量作为主成分变量；
[0159]
多元线性回归方程建立模块，用于根据选取的综合评价值较高主成分变量建立多元线性回归方程；
[0160]
显著性检验模块，用于检验所述多元线性回归方程的显著性；
[0161]
概率值选取模块，用于选取t值对应的最大概率值p
max
；
[0162]
判断模块，用于判断最大概率值p
max
是否小于等于临界值；
[0163]
若小于等于临界值，则输出用电设备能耗与各个影响因素之间的多元线性回归方程。
[0164]
关于基于多元线性回归的设备能耗预测装置的具体限定可以参见上文中对于基于多元线性回归的设备能耗预测方法的限定，在此不再赘述。
[0165]
综上，本技术具有以下优势：
[0166]
(1)使用的主成分分析法，通过少数几个主成分来揭示多个变量间的关系，通过几个主要的因素来表达出中央空调的能耗结果，在保证结果的情况下，降低了能耗的计算量。
[0167]
(2)通过多元线性回归方法计算如中央空调等没有具体运行时长及功率等不能用公式直接算出能耗的用电设备。
[0168]
(3)找出用电设备的多个影响因素，由多个影响因素的最优组合共同来预测，比用一个影响因素进行预测更有效，更符合实际。
[0169]
(4)多元线性回归可直观、快速分析出用电设备和各个影响因素之间的线性关系，可以准确的得到各个因素之间的相关程度与拟合程度的高低，提高预测的准确性。
[0170]
以上实施例的各技术特征可以进行任意的组合(只要这些技术特征的组合不存在矛盾)，为使描述简洁，未对上述实施例中的各个技术特征所有可能的组合都进行描述；这些未明确写出的实施例，也都应当认为是本说明书记载的范围。
[0171]
上文中通过一般性说明及具体实施例对本技术作了较为具体和详细的描述。应当
理解，基于本技术的技术构思，还可以对这些具体实施例作出若干常规的调整或进一步的创新；但只要未脱离本技术的技术构思，这些常规的调整或进一步的创新得到的技术方案也同样落入本技术的权利要求保护范围。