一种燃气轮机叶片寿命加速测试方法

1.本发明属于可靠性分析技术领域，特别涉及一种燃气轮机叶片寿命加速测试方法。


背景技术：

2.燃气轮机被广泛应用于发电和航空领域，先进燃气轮机的研发具有重要意义。然而，由于缺乏相关经验和技术积累，在恶劣工况下燃气轮机叶片的寿命预测一直是燃气轮机设计制造领域的薄弱环节。工业领域的寿命加速测试最早由美国空军罗姆航空发展中心提出。其目标是在合理的工程假设的基础上，利用与失效相关的物理方程和统计模型对超出正常应力水平的加速环境下的寿命特征来预测产品在正常应力下的寿命特征，从而加快测试时间。然而，这种加速寿命测试应用到燃气轮机叶片可靠性分析领域存在以下问题：1.对于燃气轮机叶片这种昂贵的工业部件，使用传统的基于实验的寿命加速测试成本极高。2.传统寿命加速测试的方法的需要使用大量测试样本以获得统计学上可信的结论。3.传统寿命加速测试需要等待叶片断裂之后才能获取数据，故障数据获取困难，实验周期较长。


技术实现要素：

3.为了克服上述现有技术的缺点，本发明的目的在于提供一种燃气轮机叶片寿命加速测试方法，以节省燃气轮机叶片寿命加速测试的时间。该发明主要基于多项式混沌方法和kriging代理模型方法，不需要进行实验，使用数学理论对燃气轮机的寿命模型进行建模，能够预测任意燃气轮机叶片壁面温度下的燃气轮机叶片寿命，对先进燃气轮机的研发具有重要意义。
4.为了实现上述目的，本发明采用的技术方案是：
5.一种燃气轮机叶片寿命加速测试方法，包括如下步骤：
6.s1，根据不确定性输入量的分布，基于混沌多项式理论，生成待求解的混沌多项式展开式和样本点坐标；
7.s2，根据所述样本点坐标，获取各个样本点的燃气轮机叶片壁面温度；
8.s3，根据所述混沌多项式展开式和各个样本点的燃气轮机叶片壁面温度，计算混沌多项式展开式系数，从而获得混沌多项式展开式的显式方程；
9.s4，根据所述混沌多项式展开式的显式方程，构造待求解的通用克里金模型；
10.s5，根据所述待求解的通用克里金模型和各个样本点的燃气轮机叶片壁面温度，求解通用克里金模型的响应面方程，即燃气轮机叶片壁面温度的计算方程；
11.s6，接收不确定输入量的分布，根据计算需求生成相应数量的抽样点的坐标；
12.s7，根据所述燃气轮机叶片壁面温度的计算方程和所述抽样点的坐标，计算每一个抽样点所对应工况的燃气轮机叶片壁面温度，再由燃气轮机叶片的壁面温度-寿命图计算每一个抽样点所对应工况的燃气轮机叶片的失效时间；
13.s8，根据所述抽样点的坐标和每一个抽样点所对应工况的燃气轮机叶片的失效时
间，计算燃气轮机叶片寿命的三参数威布尔分布的概率密度函数；
14.s9，根据所述概率密度函数，使用寿命加速测试理论测试燃气轮机叶片寿命。
15.与现有技术相比，本发明的有益效果是：
16.(1)引入不确定性理论进行燃气轮机叶片寿命的的加速寿命测试而不是像传统方法一样使用实验进行计算，用数学模型替代实验，因此能够大幅度减少成本。
17.(2)本发明通过基于通用克里金模型的多项式混沌方法的引入大幅度减少测试的样本数目。
18.(3)每一个测试样本的结果由计算机计算，不需要像传统方法一样耗费大量时间等待叶片断裂。
19.(4)该方法能够使用有限的测试样本预测任意燃气轮机叶片壁面温度下的燃气轮机叶片的寿命。
附图说明
20.图1为ge-e3燃气轮机叶形几何参数示意图。
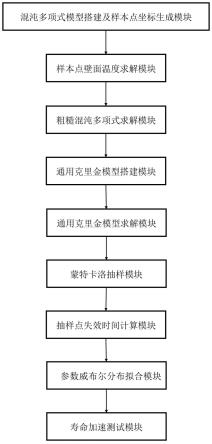
21.图2为本发明系统示意图。
22.图3为燃气轮机叶片壁面温度-寿命图。
23.图4为ge-e3燃气轮机叶片寿命的寿命加速测试结果。
具体实施方式
24.下面结合附图和实施例详细说明本发明的实施方式。
25.例：计算模型来自被广泛使用的ge_e3叶形(kwak j s,han j c.heat-transfer coefficients of a turbine blade-tip and near-tip regions[j].journal of thermophysics and heat transfer,2003,17(3):297-303.)，ge_e3叶形的几何参数见表1,各个几何参数含义见图1。
[0026]
表1ge_e3叶形的几何参数
[0027]
几何参数名称数值(mm)叶顶间隙(s)0.4凹槽深度(d)5.08肩壁厚度(g)2.29叶片高度(h)122
[0028]
参考图2，本实施例基于一种燃气轮机叶片寿命加速测试方法，包括：
[0029]
1.混沌多项式模型搭建及样本点坐标生成模块,接收不确定性输入量的分布，基于混沌多项式理论，生成待求解的混沌多项式展开式和样本点坐标。本实施例选取叶顶间隙(s)、主流入口总温(t0)、主流入口总压(p0)和入口气流角(a)作为不确定性变量，它们分别满足表2中的高斯分布。在混沌多项式理论中，数值积分节点的坐标也就是待计算的样本点坐标由公式(1)计算：
[0030][0031]
式中，n表示问题的维度，即不确定性输入量的类型数量，k表示计算精度，在本实
施例中n＝4,k＝4。表示n维k阶数值积分节点，q为常数，q＝k+n，|i|＝i1+i2+i3+
…
+ij+
…
+in，ij表示第j项展开式一维数值积分节点的序数，j＝1,2,
……
,n，表示序数为ij的一维数值积分的节点；每一个数值积分节点的坐标包含n个参数，即该数值积分节点所代表的工况的不确定性输入量。
[0032]
为了求解混沌多项式，还需要给出各个数值积分节点对应的权重w，w可由公式(2)计算：
[0033][0034]
式中,表示序数为ij的数值积分节点权重的分量，表示由各个分量组成的向量。
[0035]
表2不确定性变量的分布
[0036]
几何参数名称均值标准差叶顶间隙(s)0.4mm0.08mm主流入口总温(d)709.0k17.24k主流入口总压(g)126900pa7480pa入口气流角(h)0.0
°
0.67
°
[0037]
根据问题的维度n和计算精度k，还可以建立系统输出y的混沌多项式，也即本发明待求解的混沌多项式展开式，即式(3)。在本实施例中y为系统输出，即燃气轮机叶片壁面温度，n＝4,k＝4。
[0038][0039]
式中，a0、分别表示混沌多项式展开式各阶正交基i0、、所对应的系数，即需要求解的量，为各阶投影，θ为不确定性输入量；在实际运算中根据问题的维度n和计算精度k可以将燃气轮机叶片壁面温度y的表达式表示为：
[0040][0041]
式中，p为混沌多项式展开式的阶数，p的数值越大计算越精确，在实施例中，p设置为4。aj为第j项正交基的系数，即混沌多项式各阶正交基的系数的离散形式，ψj(ξ)为离散情况下的第j项正交基。
[0042]
2.样本点壁面温度求解模块，接受n维k阶的数值积分节点的坐标，也即样本点的坐标每一个样本点的坐标包含n个参数，这n个参数依次是这个数值积分节点所代表的
工况的叶顶间隙(s)、主流入口总温(t0)、主流入口总压(p0)和入口气流角(a)。将这n个参数输入开源计算流体力学库openfoam中即可计算该数值积分节点所代表工况的燃气轮机叶片壁面温度；对所有数值积分节点的坐标包含的参数输入开源计算流体力学库openfoam，即可获取每一个样本点所代表工况的燃气轮机叶片壁面温度。
[0043]
3.混沌多项式求解模块，接收混沌多项式模型搭建及样本点坐标生成模块计算的混沌多项式展开式和各个样本点的燃气轮机叶片壁面温度。使用galerkin投影法计算混沌多项式展开式系数从而获得混沌多项式展开式的显式方程。混沌多项式展开式系数即混沌多项式展开式各阶正交基的系数，使用galerkin投影法求解，公式如下：
[0044][0045]
式中，ψj(ξ)表示第j项正交基，为多项式内积，j(ξ)为不确定性输入量的联合概率密度函数，混沌多项式展开式的系数搭配混沌多项式展开式中的多项式各阶正交基i0、即为所求混沌多项式展开式的显式方程。该显式方程的输入为某一个工况的叶顶间隙(s)、主流入口总温(t0)、主流入口总压(p0)和入口气流角(a)，输出为该工况下的ge-e3燃气轮机叶片壁面温度。
[0046]
4.通用克里金模型搭建模块，接收混沌多项式求解模块生成的混沌多项式的显式方程，构造待求解的通用克里金模型。通用克里金模型形式如下：
[0047]
m(θ)＝f
t
(θ)β+z(θ)
ꢀꢀꢀ
(6)
[0048]
式中，f
t
(θ)为所述混沌多项式展开式的显式方程，作为通用克里金模型的回归函数，β表示回归函数的系数，z(θ)表示局部偏差的近似。
[0049]
5.通用克里金模型求解模块，接收通用克里金模型搭建模块生成的待求解通用克里金模型和样本点壁面温度求解模块生成的各个样本点的燃气轮机叶片壁面温度，获得并求解通用克里金模型的响应面方程，这个响应面方程也就是燃气轮机叶片壁面温度的计算方程。令局部偏差z(θ)的协方差矩阵为：
[0050]
e[(z(θ1)z(θ2))]＝σ2r(γ,θ1,θ2)
ꢀꢀꢀ
(7)
[0051]
式中，θ1和θ2表示样本空间中任意两个样本点，γ表示超参数。r(γ,θ1,θ2)表示θ1和θ2的空间相关函数，r(γ,θ1,θ2)的计算方法如下：
[0052][0053]
式中，n表示问题的维度，在本实施例中n等于4。γj，θ
1j
和θ
2j
表示第j维的γ，θ1和θ2。待测点θ
x
与样本点θs的关联性表示如下：
[0054]
r(θ)＝r(γ,θ
x
,θs)
t
ꢀꢀꢀ
(9)
[0055]
将样本点壁面温度求解模块所得的各样本点的燃气轮机叶片壁面温度记录到矩阵y中，式(3)中的多项式各阶正交基i0、表示为f，则通用克里金模型的响应面方程由下式计算：
[0056]
m(θ)＝f
t
(θ)β+r
t
(θ)r(γ,θ
x
,θs)-1
(y-fβ)
ꢀꢀꢀ
(10)
[0057]
6.蒙特卡洛抽样模块，接收不确定输入量的分布，根据计算需求生成相应数量的
抽样点的坐标。每一个坐标包含四个参数，分别为该抽样点的叶顶间隙(s)、主流入口总温(t0)、主流入口总压(p0)和入口气流角(a)。为了高精度地拟合威布尔分布，需要设置抽样点的数目n
point
，这个数值越大越好，在本实施例中，抽样点的数目n
point
设置为80000。使用蒙特卡洛抽样计算n
point
个抽样点的坐标的步骤如下：
[0058]
1)首先使用python的开源库random函数随机生成n
point
个分布在(0,1)之间的数值，并依次放到数组z
point
中。
[0059]
2)设第m个抽样点的坐标为(m1,m2,m3,m4)，则根据蒙特卡洛原理有：
[0060][0061][0062][0063][0064]
式中z
point
[m]为数组z
point
的第m个值，ν为辅助计算的变量，根据上面公式即可计算第m个抽样点的坐标，也就是第m个抽样点的叶顶间隙(s)、主流入口总温(t0)、主流入口总压(p0)和入口气流角(a)。
[0065]
3)对n
point
个抽样点均进行步骤2)的运算，即可获得这n
point
个抽样点的坐标。
[0066]
7.抽样点失效时间求解模块，接收蒙特卡洛抽样模块生成的抽样点坐标和通用克里金模型求解模块生成的燃气轮机叶片壁面温度的计算方程，计算每一个抽样点所对应工况的燃气轮机叶片壁面温度，再由燃气轮机叶片的壁面温度-寿命图计算每一个抽样点所对应工况的燃气轮机叶片的失效时间，燃气轮机叶片的失效时间即为它的寿命。燃气轮机叶片的壁面温度-寿命图如图3所示，其数据来自来自文献(rowe j p,freeman j w,voorhees h r.final report to the general electric company aircraft gas turbine division on effect of overheating on the creep-rupture properties of udimet 500 alloy at 16000f and 28,500 psi[r].1957.)。
[0067]
7.三参数威布尔分布拟合模块，接收抽样点失效时间求解模块生成的每一个抽样点所对应工况的燃气轮机叶片的失效时间和蒙特卡洛抽样模块生成的抽样点的坐标，计算燃气轮机叶片寿命的三参数威布尔分布的概率密度函数；三参数威布尔分布的概率密度函数满足公式(15)：
[0068][0069]
式中τ为燃气轮机叶片的失效时间，aw是威布尔分布的位置参数，bw是威布尔分布的尺度参数，cw是威布尔的形状参数。可以发现，求解出aw和bw以及cw后燃气轮机叶片寿命的威布尔分布的概率密度函数即可转化为显式计算式。本发明使用最大似然法计算燃气轮机叶片寿命的威布尔分布的aw和bw以及cw。其公式如下：
[0070]aw
＝τ
min
ꢀꢀ
(16)
[0071][0072][0073]
式中τ
min
为所有抽样点的失效时间中的最小值。λi为辅助计算的变量，λi＝τ
i-τ
min
，τi为第i个抽样点的失效时间。nw为设置的迭代步数，nw设置得越大，计算精度越高，本实施例设置nw为10000。使用公式(16)和公式(18)计算出aw和cw后代入公式(18)即可计算bw。
[0074]
8.寿命加速测试模块，接收三参数威布尔分布拟合模块生成的燃气轮机叶片寿命的威布尔分布的概率密度函数，使用寿命加速理论测试测试燃气轮机叶片寿命。寿命加速测试公式如下：
[0075][0076]
加速寿命公式的输入为失效时间τ和燃气轮机叶片壁面温度s，输出为在该燃气轮机叶片壁面温度下失效时间为τ的概率。
[0077]
图4为实施例中获得的ge-e3燃气轮机叶片壁面温度和失效时间的关系图，从图中可以发现随着壁面温度的增加，ge-e3燃气轮机叶片的失效时间迅速下降，也就是ge-e3燃气轮机叶片的寿命迅速下降。壁面温度增加40k则ge-e3燃气轮机叶片的寿命将减少6000小时左右。本发明还能够输出自定义的壁面温度下的燃气轮机叶片寿命预测，例如，当自定义温度为725k时，从图中可以发现，燃气轮机叶片寿命为13205小时。本发明基于不确定性理论对燃气轮机的寿命测试进行建模，免去的昂贵耗时的实验，而是基于数学理论进行燃气轮机叶片寿命的预测，对先进燃气轮机的研发具有重要意义。