基于两阶段并行的组合模式划分与交通分配方法

1.本发明涉及交通控制技术领域和分布式并行计算领域，尤其涉及一种基于两阶段并行的组合模式划分与交通分配方法。


背景技术：

2.城市道路交通网络的组合模式划分与流量分配问题(cmsta)是交通规划，管理与控制领域的关键性问题。在交通工程领域具有基础性作用，是科学合理评估交通治理政策，规划方案，管理措施的重要工具。大规模交通网络的组合模式划分与流量分配问题的核心是快速求解。
3.在过去的几十年里，开发高效的交通分配技术一直是交通工程师和科学家关注的焦点，不断扩张的城市交通网络和对高精度解的需要激励研究人员开发更高效快捷的交通网络流量监测技术，以用于相应交通网络流量分配。beckmann于1956年将提出了一个与交通网络流量分配问题等价的数学模型，为开发高效交通网络流量分配技术提供了一个良好的基础。尽管许多研究已经证明了求解交通分配问题(tap)的合理性能，但由于以下两个问题，计算效率仍然存在问题：一是，随着网络规模的增大，计算量将呈指数级增加，因此在实际的大规模运输网络上解决交通分配问题具有相当大的挑战性；二是，对于交通规划和管理任务，一些复杂的问题需要多次求解交通分配问题，从而产生了非常大的计算负担，如网络设计问题和多模式划分问题。因此，设计一种有效、高效的求解最优解的算法对交通运输研究具有重要意义。
4.计算硬件的快速发展为利用先进的并行计算技术并行解决tap提供了一种选择。通常，使用并行计算技术，可以将tap分解为多个独立的子问题，这些子问题可以由多个处理器并行计算。并行计算技术可以分为共享内存方法和分布式内存方法。现有的关于tap的并行研究存在以下两个问题：一是，现有的大多数研究使用共享内存方法进行，这种方法只使用一台计算机上有限数量的处理器/线程，不能充分利用计算机集群的多核心处理能力，容易使城市道路交通网络的流量监测或者分配等问题的效率低。二是，有一些研究旨在通过多台计算机集群的方式解决基于分布式内存方法的tap，然而，分布式内存方法通常需要在不同的计算节点之间进行大量的高频通信，从而大大增加了计算负担。因此，在某些应用场景下，分布式内存并行计算方法的实际性能比单线程求解的性能还要差。
5.针对上述并行计算方法存在的问题，本文虑了旅行者决策过程中的模式选择和路径选择行为，结合组合模式划分与流量分配问题的特点和分布式存储集群的结构，提出了一种创新的定制两级并行算法。两级并行算法的第一级并行采用一台计算机上的处理器，第二级并行采用多机并行，从而高效的利用分布式计算节点的计算资源。此外，本发明设计了一种分布式数据结构来快速收集和分布多计算机环境中的非结构化路径信息，可以定制化通信，减少不必要的通信耗时。因此，本发明旨在采用分布式并行方法，并将其引入交通分配领域，旨在进一步提高求解城市道路交通网络的组合模式划分与流量分配问题时的计算效率。


技术实现要素：

6.本发明所要解决的技术问题在于，近十年来，人工智能、大数据、物联网等新技术的快速发展，各类终端、电子化外场设备都产生了海量的数据，并且渗透到了交通运输行业各个业务领域中，成为了重要的生产要素。同时，随着交通网络规模的增大，计算量将呈指数级增加，因此如何在实际的大规模运输网络上快速解决组合模式划分与交通流量分配具有相当大的挑战性。
7.为解决上述技术问题，提供一种基于两阶段并行的组合模式划分与交通分配方法，包括如下步骤：
8.s1，设置集群并行、网络拓扑和需求基本参数。首先，在计算机集群设置两阶段并行，根据提出的两阶段并行技术，假设我们有t台计算机，并且每台计算机都有m个处理器。设置一台主计算机、t-1台工作计算机和t*m-1个工作处理器。其中主节点负责计算全网路径流量调整，t-1台工作节点负责od对之间的最短路计算。然后，在输入城市道路交通网络基本参数方面，输入私家车和地铁交通出行需求分布情况；所述交通网络基本参数包括各路段自由流行驶时间，路段上的交通流承载能力，路段阻抗函数，交通分配精度阈值；所述交通出行需求分布情况包括起讫点和起讫点间的交通量。
9.s2，初始化路径集。在t-1台工作节点上，使用两阶段并行技术并行计算每个起点的最短路树，以根据最短路树确定各个od对之间的最短路，对每个od对建立一个路径集合，将od对之间的最短路作为初始路径加入该od对对应的路径集合，将od对之间的出行需求加载到该od对对应的初始路径上；之后，在主节点上，在私家车模式和地铁模式之间调节车流量，将路径上的车流量叠加到道路网络中的路段上，以得到路段流量，并根据更新后的路段流量更新路段出行时间，之后将更新后的路段出行时间广播到t-1台工作节点。
10.s3，增广路径集合。在t-1台工作节点上，并行初始化路径集合。对道路交通网络上的每个od对，基于更新后的路段出行时间，使用两阶段并行技术更新每个起点的最短路树；将每个od对的最短路与od对的路径集合中的所有路径进行对比，如果现有的路径集合中没有该条最短路，就将该条最短路加入路径集合中，并将该路径上的路径流量暂时设置为0，然后将t-1台工作节点计算的od之间最新的最短路结果收集到主节点上。
11.s4，模式划分与交通流量分配。在主节点上应用组合块坐标下降和自适应梯度算法(bcd-agp)算法调整路径流量，对交通网络上的每个od对，保持路径集合不变，利用 bcd-agp算法以迭代形式比较私家车最短路径成本与地铁线路成本的运行时间在第一种情况下，计算目标函数式的二阶，然后更新私家车路径流和地铁线路流。在第二种情况下，计算目标函数式的二阶，然后更新私家车路径流和地铁线路流。从而在私家车模式和地铁模式之间调节车流量。如果车流量收敛，根据更新后路径上的车流量确定城市交通网络流量，否则返回s3，并将更新后的路段费用从主节点广播到t-1台工作节点。
12.s5，算法停止。在主节点上计算交通分配相对误差。对交通网络上的每个od对，保持路径集合不变，利用迭代算法在私家车模式和地铁模式之间调节车流量，如果车流量收敛，根据更新后路径上的车流量确定城市交通网络流量，否则返回s3，并将更新后的路段费用从主节点广播到各个工作节点。
13.具体地，s1中，在计算机集群设置两阶段并行，并给每个节点输入城市道路交通网络基本参数，具体过程包括：
14.s101，在计算机集群设置两阶段并行：
15.我们有t台计算节点，每个节点上有m个线程。每个起点的索引为o，如果 o％(t
×
m-1)等于一个线程i
th
的索引，那么基于该o的最短路树有线程i
th
计算。
16.s102，输入目标函数方程和约束条件：
[0017][0018]
约束条件：
[0019][0020][0021][0022]
式中，目标函数(1)由两项组成，分别反映了拥塞效应和od需求对网络服务水平的弹性。式(2)为流量守恒条件。方程式(3)-(4)为对决策变量(即私家车路径流和地铁线路流)的非负性约束。其中，a表示路段的集合，a∈a；w表示od对的集合，od∈w；p
od
表示od 对od间的路径集合，p∈p
od
；表示od对od间路径k上的流量；v
′a和v
″a分别表示非最短路k和最短路上的路段流量；ta(v)表示路段a的阻抗函数；表示路段-路径的关系矩阵，当路段a在od对od的第k条路径上时，取值为1，否则，取值为0；表示od 对od间的出行需求上限，q
od
是私家车模式的需求，是地铁模式的需求，其中是地铁模式下od对关联的逆需求函数
[0023]
s103，设置私家车路段阻抗函数ta(v)和地铁线路的运行成本其中，t0是自由流行驶时间，ca为路段a上的交通流承载能力，α和β为预设参数，va表示路段a的流量，具体计算公式如下：
[0024][0025]
地铁线路的运行成本可以用二进制的logit函数表示为:
[0026][0027]
式中为od对之间的地铁模式需求；and之差表示od对之间的流量需求，由od对的路径流之和决定；离散参数γ为常数，反映了需求对差旅成本的敏感性；为为 od对之间的地铁模式固定出行时间，是固定的，反映了地铁运行时间；为常数，表示地铁模式下od对之间的步行时间，即乘客从出发地到地铁站的时间和乘客从地铁站到目的地的时间之和。
[0028]
具体地，s2，s3和s5中的最短路树计算均采用两阶段并行计算的方法进行求解，在
交通网络中，在工作节点上并行地对所有起点采用单源最短路算法求解单个起点到网络上其他节点之间的最短路树。s2到3的中间，需要设置分布式数据结构在计算机节点间以一对多或多对一的形式传输(发送和接受)数据，具体过程包括：
[0029]
s201：第一种数据结构是全局分布式阵列/矩阵。od集合被t
×
m-1线程分为t
×
m-1 份od子集合并行生成新的路径。矩阵的每一行都用来存储od对的新路径。总行数等于 od对的总数。行长度是固定的和预定义的，它从第一次生成路径时设置的路径中选择最大长度的路径。该分布式矩阵收集从多个工作计算机(路径生成模块)到主计算机(路径流调节模块)生成的路径。另外，为了区分数组初始化“0”和路段索引“0”，我们需要从1计算相对值，所以我们需要在计算前加1，计算后减1。
[0030]
s202：分布式全局动态数组。当每个od对的路径流调整为零(或接近零)时，应将其从路径设置中删除。虽然每个od对有不同数量的路径，但是在分布式计算平台上记录被删除的路径索引是很困难的。分布式全局动态数组为每个od对提供固定长度的存储空间来存储不活动/删除的路径索引。这个全局动态阵列在路径生成模块中存储od对之间的路径顺序，然后在主回路中存储被删除的路径设置在路径流调整模块中。路径流调整模块完成后，存储被删除路径的全局动态阵列从主计算机广播到所有工作计算机。最后，在工作计算机上实现下一个路径生成模块之前，并行删除这些路径。
[0031]
具体地，在主节点上，对道路交通网络上的od对的路径集合w分割成若干子集合包括：
[0032]
在bcd方法中，可以使用索引分组规则将od对集分解为几个块将od对集合分成块，块中od对的个数。令od_index，表示从1开始的od 对的指标。块i∈{1,
…
,|w|/m},
[0033]
od_index＝i+k
×
g,k∈{1,
…
,m},i∈block(wi)
ꢀꢀꢀ
(7)
[0034]
剩下的od对被分组在最后一个块中。这样，同一块中的od对就不会紧密相关(耦合是指同一块中的路径有许多重叠的路段)。在每个块中，利用agp算法并行调整私家车模式与地铁模式之间的多个od对的平衡流量。
[0035]
设置迭代次数i的上限阈值，用数值maxi表示，一旦迭代次数i大于等于maxi，则当前步骤停止，计算道路交通网络在私家车模式和地铁模式的精度误差；
[0036]
判断i是否是frec的整数倍，如果i是frec的整数倍，对道路交通网络上的od对的路径集合w分割成若干子集合，否则，对一个缩小的od对的路径集合分割成若干子集合，建立一个空的受限制的od集合用来存放od对；其中若干子集合包括wi，下标i表示第 i个子集合；
[0037]
具体地，s4中，对交通网络上的每个od对，保持路径集合不变，利用组合块坐标下降和自适应梯度算法(bcd-agp)算法以迭代形式更新在私家车模式和地铁模式上的路径车流量，具体过程如下：
[0038]
s421：私家车和地铁模式之间的模式划分。在均衡状态下，每对o-d通过私家车线路的运行时间应与每对o-d在地铁线路上的运行时间相等。因此，模式划分的地铁子网函数为:
[0039][0040]
式中，为od对之间的最短成本路径；为od对之间的私家车最短成本路径。或者，由于可以重新安排eq.(8)，得到私家车模式子网络的模式划分如下:
[0041][0042]
地铁系统的模式比率为可计算为:
[0043][0044]
s422：根据路段费用，选择私家车模式或地铁模式。
[0045]
在第一种情况下，当两个模式的代价相等(即，)时，不需要重新调整两个模式之间的模式划分。
[0046]
在第二种情况下，当最短路径的成本高于过量需求的成本，即，时，出行者优先选择地铁模式。采用agp算法调整路径流量和过量需求，
[0047][0048][0049][0050]
在第三种情况下，私家车最短路径的成本低于地铁线路的成本，即旅客优先选择私家车模式。采用agp算法更新地铁线路流、非最短路径流、最短路径流如下:
[0051][0052][0053][0054]
[0055]
具体地，s4.3中，如果这个od对的精度不足，则需要利用下降算法调整这些od对中在私家车模式和地铁模式之间的路径流量，同时将这些精度不足的od对加入一个新的受限制的od集合包括：
[0056]
s431：计算od对的精度误差rg
od
；如果od对的精度误差rg
od
大于精度阈值m，使用优化方法调整od对之间的路径流量；将该od对加入od对集合
[0057]
s432：对子集合wi中的所有od对在私家车模式和地铁模式下完成流量调整后，将更新后的路径流量重新叠加到路段上，更新路段流量；
[0058]
s433：对流量受到调整的路段更新该路段的出行时间；
[0059]
s434：回到s431，更新下一个子集合中在私家车模式和地铁模式下的路径流量，并扩增od对集合
[0060]
具体地，s5中，对交通网络上的所有od对，计算整个交通网络在在私家车模式和地铁模式下流量分配的精度误差rg，如果精度误差rg大于精度阈值m，表明城市路网上的出行需求到达均衡状态，符合出行者的出行选择行为，结束计算；否则，更新m，令m＝rg/2，返回执行s3；精度误差rg为：
[0061][0062]
其中表示od对之间的最小出行时间，q
od
表示od对之间的出行需求，va表示路段流量，ta(va)表示路段出行时间，a表示交通网络上路段的集合；rg越接近0，网络交通流量越接近最优解。
[0063]
本发明与现有技术相比，具有以下有益效果：
[0064]
(1)现有交通网络流量分配技术无法进行计算机集群并行实施，也意味着无法充分利用计算机集群的多核心能力。本发明致力于高效利用计算机集群的并行计算资源，且可以在liunx，windows等多个操作系统中移植或跨平台使用，从而快速处理交通网络组合出行与流量分配问题；
[0065]
(2)本发明与现有串行或基于共享内存并行技术相比，推算速度更快，适合求解大规模交通网络组合出行与流量分配问题。可以快速评估交通基础设施，交通管理方案，交通事件对城市路网造成的影响，从而科学优化，合理指导交通设计与管理方案，对于大城市交通管理与规划项目的顺利实施具有重要作用。
附图说明
[0066]
图1是本发明的基于两阶段并行的组合模式划分与交通分配方法流程图；
[0067]
图2是本发明的基于两阶段并行的组合模式划分与交通分配方法流程图；
[0068]
图3是一个实施例中两阶段并行技术在美国芝加哥骨干网络和英国伯明翰网络的测试结果示意图。
具体实施方式
[0069]
为了使本技术的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对
本技术进行进一步详细说明。应该理解，这些描述只是示例性的，而并非要限制本发明的应用范围。
[0070]
在本文中提及“实施例”意味着，结合实施例描述的特定特征、结构或特性可以包含在本技术的至少一个实施例中。在说明书中的各个位置出现该短语并不一定均是指相同的实施例，也不是与其它实施例互斥的独立的或备选的实施例。本领域技术人员显式地和隐式地理解的是，本文所描述的实施例可以与其它实施例相结合。
[0071]
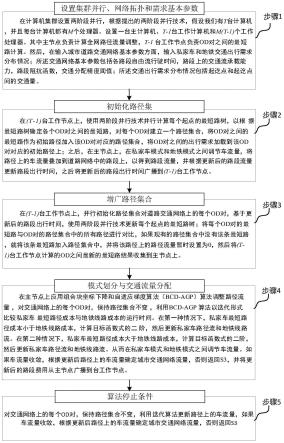
参考图1所示，图1是一个实施例的基于两阶段并行的组合模式划分与交通分配方法流程图，包括如下步骤：
[0072]
步骤1，设置集群并行、网络拓扑和需求基本参数。首先，在计算机集群设置两阶段并行，根据提出的两阶段并行技术，假设我们有t台计算机，并且每台计算机都有m个处理器。设置一台主计算机、t-1台工作计算机和t*m-1个工作处理器。其中主节点负责计算全网路径流量调整，t-1台工作节点负责od对之间的最短路计算。然后，在输入城市道路交通网络基本参数方面，输入私家车和地铁交通出行需求分布情况；所述交通网络基本参数包括各路段自由流行驶时间，路段上的交通流承载能力，路段阻抗函数，交通分配精度阈值；所述交通出行需求分布情况包括起讫点和起讫点间的交通量。
[0073]
步骤2，初始化路径集。在t-1台工作节点上，使用两阶段并行技术并行计算每个起点的最短路树，以根据最短路树确定各个od对之间的最短路，对每个od对建立一个路径集合，将od对之间的最短路作为初始路径加入该od对对应的路径集合，将od对之间的出行需求加载到该od对对应的初始路径上；之后，在主节点上，在私家车模式和地铁模式之间调节车流量，将路径上的车流量叠加到道路网络中的路段上，以得到路段流量，并根据更新后的路段流量更新路段出行时间，之后将更新后的路段出行时间广播到t-1台工作节点。
[0074]
步骤3，增广路径集合。在t-1台工作节点上，并行初始化路径集合。对道路交通网络上的每个od对，基于更新后的路段出行时间，使用两阶段并行技术更新每个起点的最短路树；将每个od对的最短路与od对的路径集合中的所有路径进行对比，如果现有的路径集合中没有该条最短路，就将该条最短路加入路径集合中，并将该路径上的路径流量暂时设置为0，然后将t-1台工作节点计算的od之间最新的最短路结果收集到主节点上。
[0075]
步骤4，模式划分与交通流量分配。在主节点上应用组合块坐标下降和自适应梯度算法 (bcd-agp)算法调整路径流量，对交通网络上的每个od对，保持路径集合不变，利用 bcd-agp算法以迭代形式比较私家车最短路径成本与地铁线路成本的运行时间在第一种情况下，计算目标函数式的二阶，然后更新私家车路径流和地铁线路流。在第二种情况下，计算目标函数式的二阶，然后更新私家车路径流和地铁线路流。从而在私家车模式和地铁模式之间调节车流量。如果车流量收敛，根据更新后路径上的车流量确定城市交通网络流量，否则返回步骤3，并将更新后的路段费用从主节点广播到t-1台工作节点。
[0076]
步骤5，算法停止。在主节点上计算交通分配相对误差。对交通网络上的每个od对，保持路径集合不变，利用迭代算法在私家车模式和地铁模式之间调节车流量，如果车流量收敛，根据更新后路径上的车流量确定城市交通网络流量，否则返回步骤3，并将更新后的路段费用从主节点广播到各个工作节点。
[0077]
具体地，本实施例使用的时间是广义的时间，包括出行者感知的行驶时间，以及行驶过程中付出的成本。
[0078]
上述基于两阶段并行的组合模式划分与交通分配方法，根据提出的两阶段并行技术，设置一台主节点和t-1台工作节点，其中主节点负责计算全网路径流量调整，t-1台工作节点负责od对之间的最短路计算。然后在每个节点上，通过获取设定城市内道路交通网络上的运行参数，设置交通流量分配精度阈值m，以及计算过程中的参数frec，使用两阶段并行方法计算每个起点的最短路树，以根据最短路树确定各个od对之间的最短路，对每个od对建立一个路径集合，然后将t-1台工作节点计算的od之间最新的最短路结果收集到主节点上，将od对之间的最短路作为初始路径加入该od对对应的路径集合，将od 对之间的出行需求加载到该od对对应的初始路径上。之后，在主节点上，在私家车模式和地铁模式之间调节车流量，将路径上的车流量叠加到道路网络中的路段上，以得到路段流量，并根据更新后的路段流量更新路段出行时间，之后将更新后的路段出行时间广播到所有工作节点。然后，在t-1台工作节点上，对道路交通网络上的每个od对，基于更新后的路段出行时间并行更新每个起点的最短路树；将每个od对的最短路与od对的路径集合中的所有路径进行对比，如果现有的路径集合中没有该条最短路，就将该条最短路加入路径集合中，并将该路径上的路径流量暂时设置为0，然后将t-1台工作节点计算的od 之间最新的最短路结果收集到主节点上。然后，在主节点上，利用bcd-agp算法以迭代形式，比较私家车最短路径成本与地铁线路成本的运行时间在第一种情况下，计算目标函数式的二阶，然后更新私家车路径流和地铁线路流。在第二种情况下，计算目标函数式的二阶，然后更新私家车路径流和地铁线路流。从而在私家车模式和地铁模式之间调节车流量。如果车流量收敛，根据更新后路径上的车流量确定城市交通网络流量，以实现对城市交通网络流量的快速高精度监测，从而实现对城市交通网络流量的快速分配，否则返回步骤3，并将更新后的路段费用从主节点广播到 t-1台工作节点。
[0079]
具体地，步骤1中，在计算机集群设置两阶段并行，并给每个节点输入城市道路交通网络基本参数，具体过程包括：
[0080]
步骤101，在计算机集群设置两阶段并行；
[0081]
我们有t台计算节点，每个节点上有m个线程。每个起点的索引为o，如果 o％(t
×
m-1)等于一个线程i
th
的索引，那么基于该o的最短路树有线程i
th
计算。
[0082]
步骤102，输入目标函数方程和约束条件；
[0083][0084]
约束条件：
[0085][0086][0087][0088]
式中，目标函数(1)由两项组成，分别反映了拥塞效应和od需求对网络服务水平的
弹性。式(2)为流量守恒条件。方程式(3)-(4)为对决策变量(即私家车路径流和地铁线路流)的非负性约束。其中，a表示路段的集合，a∈a；w表示od对的集合，od∈w；p
od
表示od 对od间的路径集合，p∈p
od
；表示od对od间路径k上的流量；v
′a和v
″a分别表示非最短路k和最短路上的路段流量；ta(v)表示路段a的阻抗函数；表示路段-路径的关系矩阵，当路段a在od对od的第k条路径上时，取值为1，否则，取值为0；表示od 对od间的出行需求上限，q
od
是私家车模式的需求，是地铁模式的需求，其中是地铁模式下od对关联的逆需求函数
[0089]
步骤103，设置私家车路段阻抗函数ta(v)和地铁线路的运行成本其中，t0是自由流行驶时间，ca为路段a上的交通流承载能力，α和β为预设参数，va表示路段a的流量，具体计算公式如下：
[0090][0091]
地铁线路的运行成本可以用二进制的logit函数表示为:
[0092][0093]
式中为od对之间的地铁模式需求；and之差表示od对之间的流量需求，由od对的路径流之和决定；离散参数γ为常数，反映了需求对差旅成本的敏感性；为为 od对之间的地铁模式固定出行时间，是固定的，反映了地铁运行时间；为常数，表示地铁模式下od对之间的步行时间，即乘客从出发地到地铁站的时间和乘客从地铁站到目的地的时间之和。
[0094]
具体地，步骤2，步骤3和步骤5中的最短路树计算均采用两阶段并行计算的方法进行求解，在交通网络中，在工作节点上并行地对所有起点采用单源最短路算法求解单个起点到网络上其他节点之间的最短路树。步骤2到3的中间，需要设置分布式数据结构在计算机节点间以一对多或多对一的形式传输(发送和接受)数据，具体过程包括：
[0095]
步骤201：第一种数据结构是全局分布式阵列/矩阵。od集合被t
×
m-1线程分为 t
×
m-1份od子集合并行生成新的路径。矩阵的每一行都用来存储od对的新路径。总行数等于od对的总数。行长度是固定的和预定义的，它从第一次生成路径时设置的路径中选择最大长度的路径。该分布式矩阵收集从多个工作计算机(路径生成模块)到主计算机(路径流调节模块)生成的路径。另外，为了区分数组初始化“0”和路段索引“0”，我们需要从1 计算相对值，所以我们需要在计算前加1，计算后减1。
[0096]
步骤202：分布式全局动态数组。当每个od对的路径流调整为零(或接近零)时，应将其从路径设置中删除。虽然每个od对有不同数量的路径，但是在分布式计算平台上记录被删除的路径索引是很困难的。分布式全局动态数组为每个od对提供固定长度的存储空间来存储不活动/删除的路径索引。这个全局动态阵列在路径生成模块中存储od对之间的路径顺序，然后在主回路中存储被删除的路径设置在路径流调整模块中。路径流调整模块完成后，存储被删除路径的全局动态阵列从主计算机广播到所有工作计算机。最后，在工作计
算机上实现下一个路径生成模块之前，并行删除这些路径。
[0097]
具体地，在主节点上，对道路交通网络上的od对的路径集合w分割成若干子集合包括：
[0098]
0在bcd方法中，可以使用索引分组规则将od对集分解为几个块将od对集合分成块，块中od对的个数。令od_index，表示从1开始的od 对的指标。块i∈{1,...,|w|/m},
[0099]
od_index＝i+k
×
g,k∈{1,
…
,m},i∈block(wi)
ꢀꢀꢀ
(25)
[0100]
步骤412：剩下的od对被分组在最后一个块中。这样，同一块中的od对就不会紧密相关(耦合是指同一块中的路径有许多重叠的路段)。在每个块中，利用agp算法并行调整私家车模式与地铁模式之间的多个od对的平衡流量。
[0101]
步骤413：设置迭代次数i的上限阈值，用数值maxi表示，一旦迭代次数i大于等于maxi，则当前步骤停止，计算道路交通网络在私家车模式和地铁模式的精度误差；
[0102]
步骤414：判断i是否是frec的整数倍，如果i是frec的整数倍，对道路交通网络上的 od对的路径集合w分割成若干子集合，否则，对一个缩小的od对的路径集合分割成若干子集合，建立一个空的受限制的od集合用来存放od对；其中若干子集合包括wi，下标i表示第i个子集合；
[0103]
具体地，步骤4中，对交通网络上的每个od对，保持路径集合不变，利用组合块坐标下降和自适应梯度算法(bcd-agp)算法以迭代形式更新在私家车模式和地铁模式上的路径车流量，具体过程如下：
[0104]
步骤421：私家车和地铁模式之间的模式划分。在均衡状态下，每对o-d通过私家车线路的运行时间应与每对o-d在地铁线路上的运行时间相等。因此，模式划分的地铁子网函数为:
[0105][0106]
式中，为od对之间的最短成本路径；为od对之间的私家车最短成本路径。或者，由于可以重新安排eq.(8)，得到私家车模式子网络的模式划分如下:
[0107][0108]
地铁系统的模式比率为可计算为:
[0109]
[0110]
步骤422：根据路段费用，选择私家车模式或地铁模式。
[0111]
在第一种情况下，当两个模式的代价相等(即，)时，不需要重新调整两个模式之间的模式划分。
[0112]
在第二种情况下，当最短路径的成本高于过量需求的成本，即，时，出行者优先选择地铁模式。采用agp算法调整路径流量和过量需求，
[0113][0114][0115][0116]
在第三种情况下，私家车最短路径的成本低于地铁线路的成本，即旅客优先选择私家车模式。采用agp算法更新地铁线路流、非最短路径流、最短路径流如下:
[0117][0118][0119][0120][0121]
具体地，步骤4.3中，如果这个od对的精度不足，则需要利用下降算法调整这些od 对中在私家车模式和地铁模式之间的路径流量，同时将这些精度不足的od对加入一个新的受限制的od集合包括：
[0122]
步骤431：计算od对的精度误差rg
od
；如果od对的精度误差rg
od
大于精度阈值m，使用优化方法调整od对之间的路径流量；将该od对加入od对集合
[0123]
步骤432：对子集合wi中的所有od对在私家车模式和地铁模式下完成流量调整后，将更新后的路径流量重新叠加到路段上，更新路段流量；
[0124]
步骤433：对流量受到调整的路段更新该路段的出行时间；
[0125]
步骤434：回到步骤431，更新下一个子集合中在私家车模式和地铁模式下的路径流量，并扩增od对集合
[0126]
具体地，步骤5中，对交通网络上的所有od对，计算整个交通网络在在私家车模式和地铁模式下流量分配的精度误差rg，如果精度误差rg大于精度阈值m，表明城市路网上的出行需求到达均衡状态，符合出行者的出行选择行为，结束计算；否则，更新m，令 m＝rg/2，返回执行步骤3；精度误差rg为：
[0127][0128]
其中表示od对之间的最小出行时间，q
od
表示od对之间的出行需求，va表示路段流量，ta(va)表示路段出行时间，a表示交通网络上路段的集合；rg越接近0，网络交通流量越接近最优解。
[0129]
具体地，图3记录了本实施例所述基于两阶段并行(tp)的组合模式划分与交通分配方法的实施过程，并与串行的自适应梯度投影(agp)交通网络流量分配技术进行比较，可以看到tp技术明显优于agp(点虚线)。即使在串行计算模式下(实线)，tp也明显优于agp，经过并行加速后，tp技术的收敛时间更短(曲线)。
[0130]
表1.本发明中的符号列表
[0131][0132]
本实施例与现有技术相比，推算速度更快，适合求解大规模交通网络组合模式划
分与交通流量分配问题。可以快速评估交通基础设施，交通管理方案，交通事件对城市路网造成的影响，从而科学优化，合理指导交通设计与管理方案，对于大城市交通管理与规划项目的顺利实施具有重要作用。
[0133]
以上实施例的各技术特征可以进行任意的组合，为使描述简洁，未对上述实施例中的各个技术特征所有可能的组合都进行描述，然而，只要这些技术特征的组合不存在矛盾，都应当认为是本说明书记载的范围。