一种基于行与列同时低秩约束的磁共振波谱重建方法

1.本发明属于数字图像处理技术领域，它特别涉及对磁共振波谱构建汉克尔矩阵并进行非凸的低秩约束以实现重建，用于高分辨率的磁共振波谱复原。


背景技术：

2.磁共振波谱是分析物质的成分、结构和相互作用的重要工具之一，被广泛应用于化学和生物工程，但其较高的维度和分辨率导致数据获取时间急剧增长。时空编码技术能对磁共振波谱在间接维度的频率信息进行并行编码，从而加快了数据采集，但为了降低对硬件设备的要求和噪声水平，需要对时空编码数据实施非均匀的欠采样，导致了部分数据的缺失。在此基础上，建立适当的磁共振波谱重建模型，并设计可行的优化算法是从欠采样的时空编码数据中重建高分辨率的磁共振波谱的关键。
3.由于二维磁共振波谱具有二元指数结构，相比约束磁共振波谱的稀疏性，对磁共振波谱构建汉克尔矩阵并约束其低秩特性更符合信号先验信息，从而提升重建磁共振波谱的质量。然而，现有的重建方法一般仅对二维磁共振波谱的行或列构建汉克尔矩阵，难以充分利用信号自身特性，同时普遍采用的核范数并不能对汉克尔矩阵进行较强的低秩约束，最终限制了磁共振波谱的重建性能。
4.事实上，对二维磁共振波谱的行与列分别构建汉克尔矩阵，并同时约束其低秩特性能够充分利用二元指数结构。另外，非凸的h
ε
范数相比核范数更近似于矩阵的秩，能有效约束矩阵的低秩特性。因此，可采用h
ε
范数同时约束磁共振波谱的行与列构建的汉克尔矩阵，并精确求解相应的重建模型，使重建的磁共振波谱更接近真实磁共振波谱。


技术实现要素：

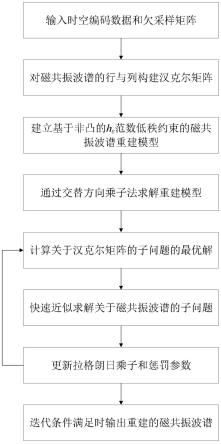
5.本发明的目的在于充分利用二维磁共振波谱的二元指数结构，提出一种基于行与列同时低秩约束的磁共振波谱重建方法。该方法对二维磁共振波谱的行与列分别构建汉克尔矩阵，并采用一种非凸的范数约束其低秩特性，进而在交替方向乘子法的优化框架下，精确求解关于重建模型中各变量的子问题，使获得的重建磁共振波谱有效抑制伪影现象，且重建的谱峰更接近于真实的谱峰。
6.具体包括以下步骤：
7.(1)输入一个二维磁共振波谱信号的时空编码数据y和欠采样矩阵u，对于待重建的具有n个行向量和m个列向量的二维磁共振波谱信号x，其第n行中第m列的元素表示为x
n，m
；
8.(2)针对x中第m列的向量xm，构建其对应的汉克尔矩阵可表示为：
[0009][0010]
其中，表示将列向量转换为汉克尔矩阵的线性算符，l表示尺寸参数；
[0011]
(3)针对x中第n行的向量xn，构建其对应的汉克尔矩阵可表示为：
[0012][0013]
其中，表示将行向量转换为汉克尔矩阵的线性算符，k表示尺寸参数；
[0014]
(4)采用非凸的h
ε
范数约束构建的汉克尔矩阵的低秩特性，表示任意矩阵l的h
ε
范数，其定义式为：
[0015][0016]
其中，σr为l的第r个奇异值，ε＞0是一个小常数；
[0017]
(5)在利用h
ε
范数同时约束x中行与列构建的汉克尔矩阵低秩特性的基础上，建立关于二维磁共振波谱的重建模型：
[0018][0019]
其中，fm表示m
×
m大小的傅里叶变换矩阵，in表示n
×
n大小的单位矩阵，表示矩阵的克罗内克积算符，vec(
·
)表示将矩阵的各列依次堆叠成向量的算符，表示向量的二范数的平方，λ表示时空编码数据保真项的正则化参数；
[0020]
(6)在重建模型中引入中间变量和并根据交替方向乘子法求解重建模型中各优化变量的子问题：
[0021]
(6a)固定x和rn，求解关于lm的子问题：
[0022][0023]
其中，β表示惩罚参数，tm表示针对lm引入的拉格朗日乘子，表示矩阵的frobenius范数的平方；
[0024]
(6b)固定x和lm，求解关于rn的子问题：
[0025][0026]
其中，zn表示针对rn引入的拉格朗日乘子；
[0027]
(6c)固定lm和rn，求解关于x的子问题：
[0028][0029]
(7)在得到各优化变量的解后，更新拉格朗日乘子tm和zn，以及惩罚参数β：
[0030][0031][0032]
β＝τβ
[0033]
其中τ＞1表示增长因子，重复步骤(6)～(7)，直到重建的磁共振波谱满足条件或迭代次数达到预设上限。
[0034]
本发明的创新点是将二维磁共振波谱的各行与各列分别构建汉克尔矩阵，通过非凸的h
ε
范数充分约束汉克尔矩阵的低秩特性；再对建立的重建模型采用交替方向乘子法求解，基于此直接计算关于汉克尔矩阵的子问题的最优解，显著提升了得到的汉克尔矩阵的低秩性与估计精度，同时快速近似求解关于磁共振波谱的子问题，获得了高分辨率的重建结果。
[0035]
本发明的有益效果：将二维磁共振波谱的行与列构建的汉克尔矩阵作为处理对象，充分利用了其二元指数结构；采用非凸的h
ε
范数约束汉克尔矩阵的低秩特性，相比现有的低秩正则函数能对矩阵进行更充分的低秩约束；基于交替方向乘子法优化求解重建模型，进而精确求解关于各变量的子问题，使获得的重建磁共振波谱恢复大量谱峰信息并去除了伪影，具有较高的分辨率。
[0036]
本发明主要采用仿真实验的方法进行验证，所有步骤、结论都在matlab8.0上验证正确。
附图说明
[0037]
图1是本发明的工作流程框图；
[0038]
图2是本发明仿真中使用的全采样时空相关波谱；
[0039]
图3是采用不同方法对采样率为25％的时空相关波谱的重建结果；
[0040]
图3是使用各方法(依次为cs方法、lrbhm方法和本发明方法)对采样率为25％的时空相关波谱的重建结果；
[0041]
图4是使用各方法(依次为cs方法、lrbhm方法和本发明方法)对采样率为25％的时空相关波谱的重建结果的误差。
具体实施方式
[0042]
参照图1，本发明是基于行与列同时低秩约束的磁共振波谱重建方法，具体步骤包括如下：
[0043]
步骤1，对二维磁共振波谱的各行与各列分别构建汉克尔矩阵。
[0044]
(1a)输入一个二维磁共振波谱信号的时空编码数据y和欠采样矩阵u，对于待重建的具有n个行向量和m个列向量的二维磁共振波谱信号x，其第n行中第m列的元素表示为x
n，m
；
[0045]
(1b)针对x中第m列的向量xm，构建其对应的汉克尔矩阵可表示为：
[0046][0047]
其中，表示将列向量转换为汉克尔矩阵的线性算符，l表示尺寸参数；
[0048]
(1c)针对x中第n行的向量xn，构建其对应的汉克尔矩阵可表示为：
[0049][0050]
其中，表示将行向量转换为汉克尔矩阵的线性算符，k表示尺寸参数。
[0051]
步骤2，根据二维磁共振波谱的二元指数结构，对各行与各列构建的汉克尔矩阵采用h
ε
范数约束低秩特性，从而建立磁共振波谱重建模型。
[0052]
(2a)采用非凸的h
ε
范数约束构建的汉克尔矩阵的低秩特性，表示任意矩阵l的h
ε
范数，其定义式为：
[0053][0054]
其中，σr为l的第r个奇异值，ε＞0是一个小常数；
[0055]
(2b)根据二维磁共振波谱的二元指数结构，利用h
ε
范数同时约束x中行与列构建的汉克尔矩阵低秩特性，以此建立关于二维磁共振波谱的重建模型：
[0056][0057]
其中，fm表示m
×
m大小的傅里叶变换矩阵，in表示n
×
n大小的单位矩阵，表示矩阵的克罗内克积算符，vec(
·
)表示将矩阵的各列依次堆叠成向量的算符，表示向量的二范数的平方，λ表示时空编码数据保真项的正则化参数。
[0058]
步骤3，通过交替方向乘子法求解建立的重建模型。
[0059]
(3a)在重建模型中引入中间变量和重建模型对应的增广拉格朗日函数的表达式为：
[0060][0061]
其中，β表示惩罚参数，tm表示针对lm引入的拉格朗日乘子，zn表示针对rn引入的拉格朗日乘子，《
·
，
·
》表示矩阵的内积算符，表示矩阵的frobenius范数的平方，根据交替方向乘子法，对重建模型中各优化变量进行求解；
[0062]
(3b)固定x和rn，求解关于lm的子问题：
[0063][0064]
该子问题能通过奇异值阈值处理实现求解，可以按照以下步骤进行：
[0065]
(3b1)对矩阵进行奇异值分解，得到：
[0066][0067]
(3b2)计算关于矩阵奇异值的阈值参数μ：
[0068][0069]
(3b3)对奇异值矩阵δ中所有对角元素进行阈值处理：
[0070][0071]
其中，th(
·
)表示阈值函数，δ表示δ中任意对角元素；
[0072]
(3b4)对δ中所有对角元素阈值处理后的结果可表示为th(δ)，则关于lm的子问题的最优解表达式为：
[0073]
lm＝pth(δ)vh[0074]
(3c)固定x和lm，求解关于rn的子问题：
[0075][0076]
该子问题也能通过奇异值阈值处理实现求解，可以按照以下步骤进行：
[0077]
(3c1)对矩阵进行奇异值分解，得到：
[0078][0079]
其中，e表示左奇异向量矩阵，q表示右奇异向量矩阵，σ表示奇异值矩阵；
[0080]
(3c2)通过阈值函数th(
·
)对奇异值矩阵σ中所有对角元素进行阈值处理，结果可表示为th(σ)，则关于rn的子问题的最优解表达式为：
[0081]rn
＝eth(σ)qh[0082]
(3d)固定lm和rn，求解关于x的子问题：
[0083][0084]
该子问题是一个大规模的最小二乘问题，可以按照以下步骤快速近似求解：
[0085]
(3d1)定义与的共轭运算，其定义式为：
[0086][0087]
[0088]
其中，表示的共轭算符，a表示任意l
×
(ν-l+1)大小的矩阵，a
k，i
表示a中第k行中第i列的元素，表示的共轭算符，b表示任意k
×
(m-k+1)大小的矩阵，b
k，i
表示b中第k行中第i列的元素，min(
·
，
·
)表示最小值函数，max(
·
，
·
)表示最大值函数，(
·
)
t
表示矩阵的转置算符；
[0089]
(3d2)利用共轭算符与计算辅助矩阵j1与j2：
[0090][0091][0092]
另外，计算ν
×
ν大小的对角权重矩阵与m
×
m大小的对角权重矩阵其中的第i个对角元素与的第i个对角元素的表达式为：
[0093][0094][0095]
(3d3)引入中间变量s，关于中间变量s的计算式为：
[0096][0097]
其中，γ＞0是一个小常数，i
mn
表示mn
×
mn大小的单位矩阵，im表示m
×
m大小的单位矩阵，(
·
)-1
表示矩阵的逆，x
last
表示上一次迭代中该子问题的解；
[0098]
(3d4)在得到中间变量s后，关于x的子问题的近似解表达式为：
[0099][0100]
其中，是m
×
m大小的傅里叶变换矩阵fm的共轭转置矩阵，uh是欠采样矩阵u的共轭转置矩阵，将得到的vec(x)转换为矩阵x即为获得的近似解。
[0101]
步骤4，在得到重建模型中各优化变量的解后，更新拉格朗日乘子tm和zn，以及惩罚参数β：
[0102][0103][0104]
β＝τβ
[0105]
其中τ＞1表示增长因子，重复步骤(3)～(4)，直到重建的磁共振波谱满足条件或迭代次数达到预设上限。
[0106]
本发明的效果可以通过以下仿真实验进一步说明：
[0107]
一、实验条件和内容
[0108]
实验条件：实验使用采样率为20％的泊松间隙采样模板；实验磁共振波谱采用真实的时空相关波谱如图2所示；采用信噪比(snr)作为重建结果的客观评价指标，其定义式为：
[0109][0110]
其中x为真实磁共振波谱，为重建磁共振波谱。snr数值越高说明重建磁共振波谱越接近真实磁共振波谱。
[0111]
实验内容：在上述实验条件下，选择磁共振波谱重建领域中具有代表性的cs方法、lrbhm方法与本发明方法进行对比。
[0112]
实验1：用本发明方法、cs方法和lrbhm方法分别对图2所示时空相关波谱的欠采样时空编码数据进行重建。其中cs方法是基于约束磁共振波谱的稀疏性，并采用迭代软阈值法求解重建模型，其重建结果为图3的a，重建误差为图4的a；lrbhm方法先对二维磁共振波谱的各行构建汉克尔矩阵，再使用这些汉克尔矩阵构建一个较大的分块汉克尔矩阵，并采用核范数约束其低秩特性，其重建结果为图3的b，重建误差为图4的b；实验中本发明方法设置尺寸参数l为n/2取整数结果，尺寸参数k为m/2取整数结果，h
ε
范数中小常数ε＝10-3
，时空编码数据保真项的正则化参数λ＝105，关于x的子问题的近似解中小常数γ＝0.01，增长因子τ＝1.05，本发明方法重建结果为图3的c，重建误差为图4的c。
[0113]
从图3的重建结果可以看出，cs方法导致重建的磁共振波谱中出现严重的伪影现象，并且只恢复出少量被减弱的谱峰；lrbhm方法虽然恢复出所有的谱峰，但导致一些谱峰的范围收缩且损失了一定的谱峰强度；本发明方法既有效的抑制了伪影现象，又保留了所有谱峰中大部分的谱峰信息。从图4的重建误差图中可以看出，本发明方法的重建误差明显少于其他方法，因此对应的重建结果最接近真实磁共振波谱。
[0114]
表1 不同磁共振波谱重建方法的snr指标
[0115]
磁共振波谱cs方法lrbhm方法本发明方法时空相关波谱8.6222.0334.72
[0116]
表1给出了图3中各方法重建结果的snr指标情况，可见本发明方法的snr值相比其他方法具有显著提高，说明本发明方法获得的重建磁共振波谱的质量最好，此结果与重建效果图相吻合。
[0117]
上述实验表明，本发明方法获得的重建磁共振波谱在视觉上，消除了大量伪影并恢复出充分的谱峰信息，对应的客观评价指标明显高于对比方法，由此可见本发明对磁共振波谱重建是有效的。