一种车辆轮胎精确建模方法及其应用
1.本发明涉及汽车动力学及其控制领域,尤其涉及轮胎动力学,具体地说是一种基于弹性迟滞理论的轮胎力特性建模方法及其应用。
背景技术:
2.目前国际上应用最为广泛的轮胎模型是魔术公式(magic formula,mf)。mf是一组用于拟合轮胎六分力数值的组合三角函数公式,模型公式巧妙,对多种工况下的轮胎力学特性有很好的表达能力。尽管mf具有相当巧妙多变的表达功能,但对未试验特性的预测能力较差,必须通过大量试验数据才能获得实用的结果。
技术实现要素:
3.本发明为克服现有技术存在的不足之处,提出一种车辆轮胎精确建模方法及其应用,以期能建立轮胎力在小滑移率与大滑移率间或小侧偏角与大侧偏角间的内在联系,从而能解决现有轮胎模型形式复杂、辨识参数繁多和计算量大等缺点。
4.为了解决上述技术问题本发采用如下技术方案:
5.本发明一种车辆轮胎精确建模方法的特点包括如下步骤:
6.步骤1、建立考虑轮胎迟滞特性的轮胎简化物理模型,并引入描述粘弹性材料的力位移特性,从而建立弹簧阻尼迟滞系统;
7.步骤1.1、将轮胎看作是由粘弹性材料的凹型支撑环和忽略弹性和阻尼的柔性高摩擦胎面环组成,从而建立轮胎简化物理模型;
8.步骤1.2、在纯纵滑工况下,令轮胎地面接触点相对轮毂偏转的角度为凹型支撑环所产生的纵向变形量;令所有凹型支撑环的纵向弹力、阻尼力与迟滞力的复合力为轮胎纵向力;
9.在纯侧偏工况下,令胎面与地面间的摩擦力挤压凹型支撑环所产生的侧向变形为轮胎侧偏角;令所有凹型支撑环的侧向弹力、阻尼力与迟滞力的复合力为轮胎侧向力;从而建立弹簧阻尼迟滞系统;
10.步骤2、结合rc算子,建立所述弹簧阻尼迟滞系统的加载与卸载过程的复合力变形关系特性模型;
11.步骤3、将纯工况下轮胎与地面的相互作用关系同样划分为加载阶段和卸载阶段;
12.步骤3.1、定义轮胎胎冠相对轮辋偏转的角度为轮胎变形角,根据加载与卸载过程的复合力变形关系特性模型,将制动过程分为加载第一阶段、加载第二阶段和卸载阶段;
13.在所述加载第一阶段:胎冠与地面间相对静止,胎冠与地面间的静摩擦力达到μfn,轮胎纵向变形角为其中,μ为路面摩擦系数,fn为轮胎垂向载荷;
14.在所述加载第二阶段:轮胎纵向变形角达到最大变形角轮胎与地面间达到最大静摩擦力;
15.在所述卸载阶段:摩擦从静摩擦向滑动摩擦过渡,直至轮胎抱死时摩擦转变为纯
滑动摩擦,轮胎力稳定到μfn;轮胎纵向变形角从最大变形角回落到
16.步骤3.2、根据滑移率从0到1的变化过程表示的是轮胎从自由转动到完全抱死的变化过程,并对应轮胎简化物理模型的纵向变形角从0压缩到并最终弹回到的过程,将轮胎力与滑移率关系曲线也分为加载第一阶段、加载第二阶段和卸载阶段;
17.在加载第一阶段时,胎冠与地面间保持无明显相对滑动;滑移率从0点到达sb;
18.在加载第二阶段时,滑移率从sb达到最佳滑移率sm;轮胎力达到最大值胎冠与地面间均无明显相对滑动;
19.在卸载阶段时,滑移率超过sm,轮胎力开始下降,直至滑移率到达1,胎冠与地面间完全滑动,轮胎力从最大值逐渐回落到μfn;
20.步骤3.3、根据侧偏角从0到90
°
的变化过程对应轮胎简化物理模型的弹簧侧向压缩,并最终部分回弹的过程,将侧向力与侧偏角的关系曲线仍分为加载第一阶段、加载第二阶段和卸载阶段;
21.在加载第一阶段,胎冠与地面间保持无明显相对滑动;侧偏角从0点到达αb;
22.在加载第二阶段,侧偏角从αb达到αm,侧向力达到附着极限胎冠与地面间维持无明显滑动;
23.在卸载阶段;当侧偏角超过αm直至到90
°
时,轮胎力从最大值逐渐回落到完全侧滑时的滑动摩擦力μfn;
24.步骤4、利用式(1)-式(5)建立sae轮胎坐标系下,基于迟滞特性的纵滑与侧偏工况的半经验轮胎模型:
[0025][0026]mz
=f(α)
·dꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(2)
[0027][0028][0029][0030]
式(1)-式(5)中,f(x)为sae坐标系下轮胎的纵向力或者侧向力,对应的自变量x为滑移率s或者轮胎的侧偏角α;mz表示轮胎的回正力矩;d表示轮胎拖距;xb、xm和xo分别表示加载起始点、最大值点和卸载终点的对应的滑移率so=1或者侧偏角αo=90
°
,其中,加载起始点和卸载终点对应的轮胎力相同;f称为缩放因子;p、q、β、r为轮胎力相应的参数;pd、qd、βd、rd为轮胎拖距相应的参数。
[0031]
本发明一种电子设备,包括存储器以及处理器,其特点在于,所述存储器用于存储
支持处理器执行所述方法的程序,所述处理器被配置为用于执行所述存储器中存储的程序。
[0032]
本发明一种计算机可读存储介质,计算机可读存储介质上存储有计算机程序,其特点在于,所述计算机程序被处理器运行时执行所述方法的步骤。
[0033]
与已有技术相比,本发明的有益效果体现在:
[0034]
1、本发明提出了一种考虑轮胎压缩迟滞的轮胎简化物理模型,将轮胎看作是由一定数量的绕轮辋一周的具有粘弹性的凹型支撑环和忽略弹性和阻尼的柔性高摩擦胎面环组成,胎面环在受到地面力后压缩凹型弹性支撑环产生轮胎力,该模型强调胎体变形在轮胎力产生过程的重要作用,规避了胎面与路面摩擦的复杂过程,简化了轮胎力的计算过程。
[0035]
2、本发明深入分析了弹簧阻尼迟滞系统力学特性,并结合rc算子,分别建立了弹簧阻尼迟滞系统加载与卸载过程的力变形关系特性模型,引入了rc算子迟滞模型,为后续描述胎体变形过程中的轮胎力位移特性带下基础。
[0036]
3本发明将纯工况下轮胎与地面的相互作用关系同样划分为加载阶段和卸载阶段,分析轮胎加载与卸载阶段力学特性变化规律。通过对纯工况下轮胎加载与卸载力学特性规律的研究,揭示了小滑移率或侧偏角下的轮胎力特性与大滑移率或大侧偏角下的轮胎力特性的内在关联。从而对纯工况下的轮胎力学特性做出了全新的理论解释,并建立了新型的轮胎模型hystire,从而获得了一个形式简单、辨识少和计算小等优点的轮胎模型。
附图说明
[0037]
图1a为凹环轮胎模型的示意图;
[0038]
图1b为凹环轮胎模型在纵向力下的轮胎变形示意图;
[0039]
图1c为凹环轮胎模型在侧向力下的轮胎变形示意图;
[0040]
图2为轮胎纵滑工况下f
x-关系曲线图;
[0041]
图3为轮胎纵滑工况下f
x-s关系曲线图;
[0042]
图4为轮胎侧偏f
y-α关系曲线图;
[0043]
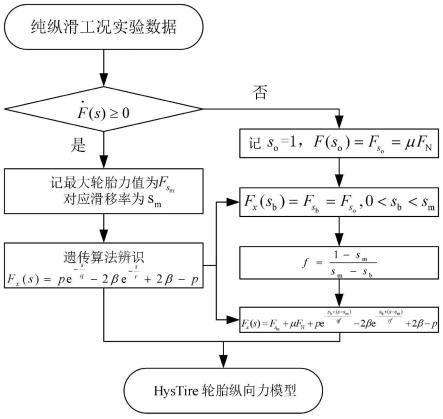
图5为hystire轮胎模型中纵滑特性的辨识流程图;
[0044]
图6为hystire轮胎模型中侧偏特性的辨识流程图。
具体实施方式
[0045]
本实施例中,一种车辆轮胎精确建模方法是开发一种所用实验数据少、流程简单的轮胎力特性建模方法,具体的说,包括如下步骤:
[0046]
步骤1、建立考虑轮胎迟滞特性的轮胎简化物理模型,并引入描述粘弹性材料的力位移特性,从而建立弹簧阻尼迟滞系统;
[0047]
步骤1.1、参见图1a所示,将轮胎看作是由一定数量的绕轮辋一周的具有粘弹性材料的凹型支撑环和忽略弹性和阻尼的柔性高摩擦胎面环组成,胎面环在受到地面力后压缩凹型支撑环产生轮胎力,从而建立轮胎简化物理模型;
[0048]
步骤1.2、图1b为所建立的轮胎模型在纯纵滑工况下的轮胎变形示意图,在纯纵滑工况下,胎面与地面间的摩擦力压缩凹型支撑环产生纵向变形,变形量大小即为轮胎地面接触点相对轮毂偏转的角度,令轮胎地面接触点相对轮毂偏转的角度为凹型支撑环所产生
的纵向变形量;令所有凹型支撑环的纵向弹力、阻尼力与迟滞力的复合力为轮胎纵向力;
[0049]
图1c为纯侧偏工况下轮胎变形示意图,在纯侧偏工况下,令胎面与地面间的摩擦力挤压凹型支撑环所产生的侧向变形为轮胎侧偏角;根据图1c,轮胎静止时变形量大小即为轮胎地面接地印迹中心与车轮平面偏移的距离,轮胎滚动时,变形量表现为接触印迹中心与车轮平面夹角的大小,也即侧偏角的大小;令所有凹型支撑环的侧向弹力、阻尼力与迟滞力的复合力为轮胎侧向力;凹环轮胎模型将轮胎各向简化成为弹簧阻尼迟滞系统,定性解释轮胎力和力矩产生和作用机理。
[0050]
步骤2、结合rc算子,建立弹簧阻尼迟滞系统的加载与卸载过程的复合力变形关系特性模型;
[0051]
步骤3、将纯工况下轮胎与地面的相互作用关系同样划分为加载阶段和卸载阶段;
[0052]
步骤3.1、定义轮胎胎冠相对轮辋偏转的角度为轮胎变形角,根据加载与卸载过程的复合力变形关系特性模型,参见图2所示为轮胎纵滑工况下f
x-关系曲线,将制动过程分为加载第一阶段、加载第二阶段和卸载阶段;
[0053]
在加载第一阶段:随着地面施加给轮胎的制动力增加,轮胎变形角逐渐增大,胎冠与地面间相对静止,胎冠与地面间的静摩擦力达到μfn,轮胎纵向变形角为其中,μ为路面摩擦系数,fn为轮胎垂向载荷;
[0054]
在加载第二阶段:此时由于胎冠表面与路面黏着接触作用,轮胎力继续增加,轮胎变形角进一步增大,直至轮胎纵向变形角达到最大变形角轮胎与地面间达到最大静摩擦力;
[0055]
在卸载阶段:随着胎冠与地面间滑动成分增加,摩擦从静摩擦向滑动摩擦过渡,地面所提供的摩擦力难以维持轮胎变形,直至轮胎抱死时摩擦转变为纯滑动摩擦,轮胎力稳定到μfn;轮胎纵向变形角从最大变形角回落到第二加载阶段与卸载阶段是粘弹性弹簧阻尼迟滞系统在相同形变范围下的加载曲线与卸载曲线,所围成的区域代表能量损失。
[0056]
步骤3.2、由于在轮胎实际应用中,变形角难以测量,而用来表征车轮滑动成分的滑移率与轮胎变形角之间存在着一一对应的关系。参见图3所示为轮胎纵滑工况下f
x-s关系曲线。根据滑移率从0到1的变化过程表示的是轮胎从自由转动到完全抱死的变化过程,并对应轮胎简化物理模型的纵向变形角从0压缩到并最终弹回到的过程,将轮胎力与滑移率关系曲线也分为加载第一阶段、加载第二阶段和卸载阶段三个过程;滑移率采用车速与轮速的差值计算,也即轮辋与胎冠间的速度差;
[0057]
在加载第一阶段时,即在小滑移率时,速度差来自胎体的纵向压缩,胎冠与地面间保持无明显相对滑动,滑移率从0点到达sb;
[0058]
在加载第二阶段时,滑移率从sb达到最佳滑移率sm;轮胎力达到最大值胎冠与地面间均无明显相对滑动;
[0059]
在卸载阶段时,滑移率超过最佳滑移率sm,胎冠与地面间滑动成分逐渐增加,轮胎力开始下降,直至滑移率到达1,胎冠与地面间完全滑动,轮胎力从最大值逐渐回落到μfn;对应图2中f
x-曲线的卸载阶段的轮胎力变化过程。通过以上分析,可以得出图3中mn段与mo段是同样的纵向变形角下在相同时间内不同横坐标下的卸载路径曲线。
[0060]
步骤3.3、侧向力变化过程同样是在特定的侧偏角下达到最大值后开始下降,采用
同样的方法对轮胎侧偏工况分析。如图4所示轮胎侧偏f
y-α关系曲线。根据侧偏角从0到90
°
的变化过程对应轮胎简化物理模型的弹簧侧向压缩,并最终部分回弹的过程,将侧向力与侧偏角的关系曲线仍分为加载第一阶段、加载第二阶段和卸载阶段三个过程;
[0061]
在加载第一阶段,胎冠与地面间保持无明显相对滑动;侧偏角从0点到达αb;
[0062]
在加载第二阶段,侧偏角从αb达到αm,侧向力达到附着极限胎冠与地面间维持无明显滑动;
[0063]
在卸载阶段;当侧偏角超过αm直至到90
°
时,轮胎力从最大值逐渐回落到完全侧滑时的滑动摩擦力μfn;
[0064]
步骤4、利用式(1)-式(5)建立sae轮胎坐标系下,基于迟滞特性的纵滑与侧偏工况表达统一的半经验轮胎模型:
[0065][0066]mz
=f(α)
·dꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(2)
[0067][0068][0069][0070]
式(1)-式(5)中,f(x)为sae坐标系下轮胎的纵向力或者侧向力,对应的自变量x为滑移率s或者轮胎的侧偏角α;mz表示轮胎的回正力矩;d表示轮胎拖距;xb、xm和xo分别表示加载起始点、最大值点和卸载终点的对应的滑移率so=1或者侧偏角αo=90
°
,其中,加载起始点和卸载终点对应的轮胎力相同;f称为缩放因子;p、q、β、r为轮胎力相应的参数;pd、qd、βd、rd为轮胎拖距相应的参数。
[0071]
如图5所示给出hystire轮胎模型在纯纵滑工况下的辨识流程,当时,即纵向力随着滑移率的增大而增大,直至纵向力达到最大值,此时滑移率记为sm,称为最大值点。此时在0-sm阶段,采用遗传算法对hystire轮胎模型的纵滑工况进行拟合辨识,得到拟合参数p、q、β、r,即可得到0-sm阶段的纵向力模型。当时,变滑移率化范围从sm至滑移率最大值so=1,so称为卸载终点,对应的轮胎力为在0-sm阶段中存在一点sb,使得称sb为加载起点,sb点通过0-sm阶段的纵向力模型反解得到。将已拟合的参数p、q、β、r,以及sb、sm、so、μfn代入hystire轮胎模型,即可得到s
m-1阶段的纵向力模型,至此便可获得轮胎纵向力特性模型。
[0072]
图6给出hystire轮胎模型在纯侧偏工况下的辨识流程,当时,即侧偏力随着侧偏角的增大而增大,直至侧偏力达到最大值,此时侧偏角记为αm,称为最大值点。此时在0-αm阶段,采用遗传算法对hystire轮胎模型侧偏工况进行拟合辨识,得到拟合参数p、q、β、r,即可得到0-αm阶段的侧偏力模型。当时,侧偏角变化范围从αm至测试最大侧偏角αo=90
°
,αo称为卸载终点,对应的侧偏力为在0-αm阶段中存在一点αb,使得称αb为加载起点,αb可通过0-αm阶段的侧偏力模型反解得到。将已拟合的参数p、q、β、r,以及αb、αm、αo、代入hystire轮胎模型,即可得到α
m-αo阶段的侧偏力模型。已知轮胎侧偏力模型,回正力矩模型可通过辨识出轮胎拖距d得到,采用遗传算法对hystire轮胎模型回正力矩mz进行拟合,得到拟合参数pd、qd、βd、rd,即可获取轮胎的侧偏特性模型。
相关技术
网友询问留言
已有0条留言
- 还没有人留言评论。精彩留言会获得点赞!
1