一种基于柱面压头接触的涂层结构界面破坏预测方法

1.本发明涉及结构可靠性分析技术领域，尤其涉及一种基于柱面压头接触的涂层结构界面破坏预测方法。


背景技术：

2.随着涂层由块状结构向层状结构发展的趋势，涂层的接触力学分析在力学领域具有重要意义。接触理论的发展可以追溯到1882年赫兹发表的经典论文“关于弹性固体的接触”。为了了解材料在外力作用下力学性质的变化，约翰逊(johnson)等人(1971)对材料的光学性质进行了研究，提出了jkr(k.l.johnson(约翰逊)k.kendall(肯德尔)和a.d.roberts(罗伯茨))接触理论来描述接触应力分布、接触曲率半径、弹性模量和材料表面能之间的关系，并分析了接触力对接触过程的影响、压痕卸载、粘弹塑性体的滚动接触等一系列问题。2015年，陈(chen)等人提出给出了椭圆形接触三维力-电磁耦合的解析解，得到的半无限体接触力学理论是进行块状材料力学分析的基础。从2019年到2020年，瓦西列夫(vasiliev,a.s.)等人对横观各向同性电弹性功能梯度压电材料导电锥形压头的压痕问题进行了详细的分析，发现涂层的存在足以改变接触特性。这些工作为更深入地研究极性材料的机电耦合现象提供了理论支持，对层状结构进行更全面的理论分析尤为关键。然而，如何利用压痕实验来检测位移响应，准确、定量地确定涂层材料的材料和界面性质仍然是一个难题。然而，利用接触力学获得涂层的应力场和弹性半空间区域来测量涂层材料参数是一种可行的方法。而且，采用接触式方式，在现有的压痕仪上更容易搭建扩展模块。接触问题的精确解对于压痕技术有着重要的应用，这对于测量新材料的特性是有价值的。传统无涂层结构接触问题的解析解可用于预测其弹塑性性能。最常见的三种接触形式是球面接触、圆锥接触和柱面接触，它们的无涂层理论体系是系统的：陈(chen,w.q.)等人(2010)给出了无涂层三维球面、锥面和柱面接触的一般解。对于涂层结构的接触理论，球面接触和圆锥接触问题已有研究，本文针对的是柱面摩擦接触问题。
3.对不同类型的接触力学问题进行研究是有必要的。早期，成(cheng)等人(1999)提出了一种新的研究方法，通过数值模拟和量纲分析方法研究，应力-应变关系可能无法通过单独使用锥形或锥体压头的加载和卸载曲线来唯一确定，刀-苏雷什(dao-suresh)等人(2001)也研究了材料参数测量的唯一性。在不同压头作用下引入的压痕形态信息可以提高测量精度，我们期望构建一个更全面的理论来提高表征测量的准确性。基于这些研究和思考，我们决定进一步研究涂层结构的接触力学行为。早期，法布里坎特(fabrikant,v.i.)(1988)研究了圆柱接触问题，导出了弹性体位移场和应力的显式表达式。汉森(hanson,m.t.(1994)给出了横观各向同性半空间中垂直或倾斜滑动圆形平板凸模弹性场的精确表达式。2008年，斯内登(sneddon)和伊恩(ian n.)也分析了无限大半空间上的平头圆柱荷载问题，指出该问题的研究在土力学，特别是地基安全问题上具有重要的应用价值。在本文中我们没有详细说明这一应用的背景，但也希望对今后层状土力学的研究有所帮助。后来，人们对功能材料(功能梯度电磁弹性材料和横观各向同性热弹性材料)的接触问题进行了更
多的研究，并与盖(ke,l.l.)等人进行了比较深入的研究。对功能梯度材料的接触问题进行了深入研究。这些接触问题的研究有望为未来微纳米级的压痕实验提供理论基础，为机器人和防粘爪的仿生设计提供指导，为功能材料表征技术的发展提供理论基础。
4.涂层被广泛用于提高结构的可靠性和耐久性，特别是改善表面附近的磨损、腐蚀和耐热性。用涂层接触理论可以区分涂层半空间表面和未涂层半空间表面的应力，还可以分析和讨论使用功能梯度涂层与常规均匀涂层相比的优缺点，以指导涂层参数的测量和设计。精密仪器的应用对涂层材料有严格的要求，在涂层结构的制造中，很难给出详细、准确的涂层结构在不同制造工艺下的性能指标，系统的接触力学理论是制定涂层结构应用行业标准的关键。大多数电子芯片都是层状结构。在可靠性试验和焊接过程中会产生很大的界面应力。当界面应力达到临界值时，界面将发生分层。扫描探针显微镜和纳米压痕实验技术已经出现，用于探索界面安全状态和表征材料性能。这些技术依赖于薄涂层的各种3d接触力学的解析计算。涂层结构的精确解有助于确定临界载荷和预测界面失效区域的大小。由于涂层材料的应力集中、结合强度差、脆性等原因，界面失效是一种普遍现象。由于涂层和基体之间的材料特性不匹配，很难避免界面应力集中。因此，对涂层系统中的接触力学问题进行理论上的、准确的定量分析是很有价值的。分析材料性能与界面应力的关系以及涂层厚度与界面应力的关系也具有重要意义。这些研究可用于涂层体系设计中涂层材料的选择、涂层厚度的确定和界面分层面积的预测。接触力学的研究有助于开发各种扫描探针显微镜，并可将力学科学与材料科学联系起来。薄层结构的接触理论还有待进一步完善，选择合适的分析方法来解决薄层结构的接触问题具有重要意义。由于基材与涂层的体积比较大，以及薄层与基材结合时材料参数的不同，可能会导致界面应力失配。力学性能的测试和表征是表面技术设计/检验的重要内容，是涂层技术改进的基础。
5.研究涂层的方法有很多。到目前为止，学者们已经做了大量的实验来研究各种材料的不同特性。通过使涂层承受循环/重复载荷和滑动，涂层的断裂韧性机理得到了研究。法瓦什(favache)等人对涂层的断裂进行了研究，关(guan)重点研究了涂层承载能力的优化。考虑到实验成本，理论分析可以指导实验减少资源损失。学者们努力寻找合适的数学方法来描述涂层的力学行为。建立涂层结构接触问题的数学模型并进行数学分析具有重要意义。有限元法(fem)和边界元法(bem)是解决涂层结构问题的主要数值计算方法。主要的分析方法有积分变换法(itm)、传递矩阵法(tmm)和经典解法(csm)。有限元在数值分析中占有主导地位。有限元作为数值平台的主流，可以进行几乎所有的工程力学建模分析。如果涂层结构非常薄，网格划分必须非常精细，那么有限元体就容易变形。因此，很难保证有限元体的有效性和分析的准确性。边界元法能够提高精度，因为它直接在边界上离散以求取值。然而，它需要与边界条件相关的格林函数。在不同的情况下会有几乎奇异的积分需要解决是一个挑战。itm包括傅立叶积分变换、拉普拉斯积分变换、梅林积分变换和汉克尔积分变换，是求解微分方程的常规方法。积分变换有助于减少原偏微分方程的自变量个数。利用傅立叶积分变换技术，马(ma,j.)等人研究了功能梯度磁电弹性涂层在导电平板冲头作用下的滑动摩擦接触，以及苏(su,j.)等人研究了功能梯度压电涂层在导电冲头作用下的微动接触问题，利用傅立叶积分变换技术将这些问题归结为耦合的柯西奇异积分方程。利用傅立叶和拉普拉斯积分变换，艾尔沙德(ershad,h.)研究了含压电涂层的裂纹非均匀衬底的瞬态响应。上述三种方法各有优缺点，涂层接触力学分析选用了通用求解法。
6.作为一种经典力学方法，一般求解法是根据力学模型的控制方程求解偏微分方程，在边界条件下得到精确解。由于数学的复杂性，用通解法求解整个应力场和位移场的解析解并不容易。根据文献，尚未得到摩擦圆柱平头接触下3d横向各向同性涂层结构的精确解。本文使用调和函数研究了3d接触力学，导出了涂层结构在两种情况下(无摩擦接触和摩擦接触)的精确解。在数值例子和分析部分讨论了应力分布、力学失效、应力分量分布以及涂层厚度对界面应力的影响。该方法能有效克服因基材与涂层尺寸比过大而导致涂层内部物理参数获取不准确的问题。该研究可以指导圆柱平头接触下涂层结构的实验。


技术实现要素：

7.本发明的目的是为了克服以上现有技术存在的不足，提供了一种基于柱面压头接触的涂层结构界面破坏预测方法。
8.本发明的目的通过以下的技术方案实现：一种基于柱面压头接触的涂层结构界面破坏预测方法，在没有摩擦接触的情况下，包括以下步骤：
9.s101、在没有摩擦接触的情况下，横向各向同性涂层结构在圆柱坐标中考虑，所述涂层的厚度为h，所述涂层的范围为0≤z≤h，所述涂层与半无限基体完美结合，所述半无限基体的范围为z≤0，所述涂层的自由表面为z＝h，所述自由表面在光滑圆柱的接触荷载n的等式(5)为：
[0010][0011]
其中，所述r的范围为0≤r≤a，所述a是接触半径，所述pz是作用在锥凹形压头上的压痕载荷；
[0012]
s102、在所述涂层中，调和函数假定为以下等式(6)，所述等式(6)为：
[0013][0014]
所述等式(6)包括等式(7)，所述等式(7)包括以下公式：
[0015][0016][0017]
其中，所述n＝1,2,
···
,∞、所述j＝1,2、所述和所述a
njk
是待定系数，所述等式(7)包括等式(8)，所述等式(8)包括以下公式：
[0018][0019][0020]
其中，所述等式(8)包括等式(9)，所述等式(9)包括以下公式：
[0021][0022][0023][0024][0025]
s103、将所述等式(6)和所述等式(7)代入等式(c6)中得到等式(10)，所述等式(10)包括以下公式：
[0026][0027][0028][0029][0030][0031][0032]
其中，所述等式(10)包括等式(a3.1)，所述等式(a3.1)包括以下公式：
[0033][0034][0035][0036][0037][0038]
[0039][0040][0041][0042][0043][0044][0045]
其中，所述i和所述j和所述表示材料的坐标方向，所述c
ij
(i,j＝1,2,
…
,6)表示刚度系数，所述sj涂层四次多项式方程的特征值(0《z《h)，所述kj、所述mj和所述ωj均为材料特征值系数；
[0046]
其中，所述等式(c6)包含以下公式：
[0047][0048][0049][0050][0051]
和
[0052][0053]
其中，所述
[0054]
所述等式(c6)包括等式(c7)，所述等式(c7)包括以下公式：
[0055][0056][0057]
mj＝2c
66-ω
1jsj2
、
[0058]
和
[0059][0060]
所述和a
njk
均为待定系数；
[0061]
s104、在基体z≤0中，调和函数假定为以下等式(11)为：
[0062][0063]
所述等式(11)包括等式(12)，所述等式(12)的公式为：
[0064][0065]
所述a
′
njk
是待定系数，所述等式(12)包括等式(13)，所述等式(13)为：
[0066][0067]
所述等式13包括等式(14)，所述等式(14)包括以下公式：
[0068][0069][0070]
其中，所述z
′
njk
为坐标系数。
[0071]
s105、将所述等式(11)和所述等式(12)代入所述等式(c6)中得到等式(15)，所述等式(15)包括以下公式：
[0072][0073][0074][0075][0076][0077][0078]
其中，所述等式(15)包括等式(a3.2)，所述等式(a3.2)包括以下等式：
[0079][0080][0081][0082][0083][0084]
s106、所述在自由面z＝h上边界条件的等式(16)设定为以下公式：
[0085]
在0≤r≤a的范围内：
[0086]
在r＞a的范围内：
[0087][0088]
s107、所述表面z＝0上的界面连续性条件的等式(17)设定为以下公式：
[0089][0090][0091][0092][0093]
s108、根据所述等式(10)，将所述等式(16)分解，得到等式(18)和等式(19)：
[0094]
所述等式(18)包括以下公式：
[0095]
在0≤r≤a的范围内：
[0096]
在r＞a的范围内：
[0097][0098][0099]
所述等式(19)包括以下公式：
[0100][0101]
s109、根据所述等式(10)和所述等式(15)，将所述等式(17)分解得到等式(20)，所述等式(20)包括以下公式：
[0102][0103]
[0104][0105][0106]
s110、确定待定系数a
1jk
、a
′
1jk
、a
njk
、a
′
njk
和
[0107]
更优的选择，所述步骤s110中的a
1jk
、a
′
1jk
、a
njk
、a
′
njk
和的确定过程包括以下步骤：
[0108]
s1101、将等式(a3.1)代入所述等式(18)，得到等式(a4.1)，所述等式(a4.1)包括以下公式：
[0109][0110][0111][0112]
s1102、将所述等式(a3.1)代入所述等式(19)得到等式(a4.2)，所述等式(a4.2)包括以下公式：
[0113][0114][0115][0116][0117][0118][0119][0120]
其中，所述m＝1,2,
···
，2n-1)；
[0121]
s1103、将等式(a3.1)和等式(a3.2)代入所述等式(20)得到等式(a4.3)，所述等式(a4.3)包括以下公式：
[0122][0123][0124][0125][0126]
所述k＝1,2,
···
,2n；
[0127]
s1104、通过所述等式(a4.1)得到通过所述等式(a4.3)求解得到a
1jk
和通过所述等式(a4.2)求解得到通过所述等式(a4.3)求解得到a
njk
和a
′
njk
，所述等式(a4.3)包括8n个方程，通过等式(a4.2)求解，得到所述(a4.2)包括4(n+1)个方程。
[0128]
一种基于柱面压头接触的涂层结构界面破坏预测方法，在存在摩擦接触的情况下，包括以下步骤：
[0129]
s201、在横向各向同性涂层结构在柱面坐标中考虑，所述涂层的厚度为h，所述涂层的范围为0≤z≤h，所述涂层与半无限长基体z≤0完美结合，所述涂层的自由表面z＝h承受以下摩擦圆柱体接触载荷nf：
[0130][0131]
其中，所述r的范围为0≤r≤a，所述f＝f
x
+ify；
[0132]
s202、在所述涂层中，假定调和函数，所述调和函数的等式(22)包括以下公式：
[0133][0134][0135]
其中，所述等式(22)包括等式(23)，所述等式(23)包括以下公式：
[0136][0137][0138][0139][0140]
其中，所述等式(23)包括等式(24)，所述等式(24)包括以下公式：
[0141][0142][0143][0144][0145]
[0146][0147][0148][0149]
其中，所述b
n0
、所述所述b
njk
和所述是待定系数，所述等式(24)包括等式(25)，所述等式(25)包括以下公式：
[0150][0151][0152][0153][0154]
s203、将所述等式(22)和所述等式(23)代入所述等式(c6)得到等式(26)，所述等式(26)包括以下公式：
[0155][0156][0157][0158][0159][0160][0161]
所述等式(26)包括等式(b3.1)，所述等式(b3.1)包括以下公式：
[0162]
[0163][0164][0165][0166][0167][0168][0169]
[0170][0171][0172][0173][0174]
s204、在所述基体中，假定调和函数的等式(27)包括以下形式：
[0175][0176][0177]
其中，所述等式(27)包括等式(28)，所述等式(28)包括以下公式：
[0178][0179][0180]
所述等式(28)包括等式(29)，所述等式(29)包括以下公式：
[0181][0182][0183][0184][0185]
其中，所述b
′
n0
和所述b
′
njk
是待定系数，所述等式(29)包括等式(30)，所述等式(30)包括以下公式：
[0186][0187][0188]
s205、将所述等式(27)和所述等式(28)代入所述等式(c6)，得到等式(31)，所述等式(31)包括以下公式：
[0189][0190][0191][0192][0193][0194][0195]
其中，所述等式(31)包括等式(b3.2)，所述等式(b3.2)包括以下公式：
[0196][0197][0198][0199]
[0200][0201][0202]
s206、在所述自由面z＝h上的边界条件的等式(32)设定为以下公式：
[0203][0204]
在范围为0≤r≤a的等式为：
[0205]
在范围为r＞a的等式为：(32)
[0206]
s207、表面z＝0上的界面连续性条件的等式(33)设定为以下公式：
[0207][0208][0209][0210][0211]
s208、根据等式(26)，将等式(32)分解得到等式(34)和等式(35)，所述等式(34)包括以下公式：
[0212]
在0≤r≤a范围内的公式为：
[0213]
在r＞a范围内的公式为：
[0214][0215]
所述等式(35)包括以下公式：
[0216][0217][0218]
s209、根据所述等式(26)和等式(31)，将所述等式(33)分解，得到等式(36)，所述等式(36)包括以下公式：
[0219][0220][0221][0222][0223]
s210、确定待定系数b
10
、b
′
10
、b
1jk
、b
′
1jk
、b
n0
、b
′
n0
、b
njk
、b
′
njk
、和
[0224]
更优的选择，所述步骤s210中的b
10
、b
′
10
、b
1jk
、b
′
1jk
、b
n0
、b
′
n0
、b
njk
、b
′
njk
、和的确定过程包括以下步骤：
[0225]
s2101、将等式(b3.1)代入所述等式(34)，得到等式(b4.1)，所述等式(b4.1)包括以下等式：
[0226][0227][0228][0229]
s2102、将等式(b3.1)代入所述等式(35)，得到等式(b4.2)，所述等式(b4.2)；
[0230][0231][0232][0233][0234][0235][0236][0237][0238]
所述n＝1,2,
···
,∞，所述m＝1,2,
···
,2n-1；
[0239]
s2103、将所述等式(b3.1)和等式(b3.2)代入所述等式(36)，得到等式(b4.3)，所述等式(b4.3)包括以下公式；
[0240][0241][0242][0243][0244][0245][0246]
所述n＝1,2,
···
,∞；；所述k＝1,2,
···
,2n；
[0247]
s2104、通过所述等式(b4.1)求得和通过所述等式(b4.3)求得b
10
，b
′
10
、b
1jk
和b
′
1jk
，通过所述等式(b4.2)求解得到和通过所述等式(b4.3)求解得到b
n0
，b
′
n0
，b
njk
和b
′
njk
，所述(b4.3)包括8n+2个方程，通过所述等式(b4.2)求解得到和
所述等式b4.2包括8n+5个方程。
[0248]
本发明相对现有技术具有以下优点及有益效果：
[0249]
本发明通过一种基于柱面压头接触的涂层结构界面破坏预测方法，推导了圆柱凸模摩擦接触下横观各向同性弹性涂层结构的三维精确解，数值计算显示了良好的收敛性、高精度、高效率和稳定性，说明了有限元方法与该理论在应力奇异性分析中的不同之处，说明了该理论的有效性和适用性，所提出的理论将成为界面失效问题分析和材料参数确定的基础，也为今后利用深度学习解决接触力学问题提供了高精度样本的基础。
附图说明
[0250]
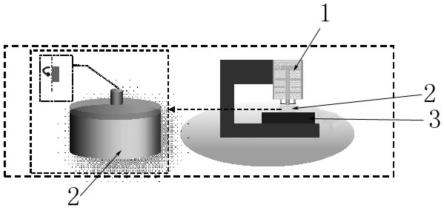
图1是本发明一种基于柱面压头接触的涂层结构界面破坏预测方法的使用示意图；
[0251]
图2是本发明一种基于柱面压头接触的涂层结构界面破坏预测方法的使用方式正视图；
[0252]
图3是本发明一种基于柱面压头接触的涂层结构界面破坏预测方法的涂层结构镜像过程示意图；
[0253]
附图中各部件的标记：1-载重架；2-样品；3-支撑台；4-涂层；5-基体。
具体实施方式
[0254]
下面结合附图和具体实施例对本发明的发明目的作进一步详细地描述,实施例不能在此一一赘述,但本发明的实施方式并不因此限定于以下实施例。
[0255]
如图1所示，一个典型的涂层结构的压痕实验，平行于横向各向同性平面的涂层表面由圆柱体刚性压头挤压，力pz穿过圆柱体的中心轴，作用于距离接触区域足够远的地方，求解给出了横观各向同性涂层结构弹性场的精确解。
[0256]
如图2所示，表示涂层表面上的镜像点，pi表示界面上的镜像点，n表示镜像顺序。
①
：均匀半空间模型的初始镜像点为表面满足边界条件。
②
：涂层的存在会改变边界条件，因此镜像点的引入使界面z＝0满足界面连续性条件，从而使上表面不满足边界条件。
③
和
④
：因此，如几何表达式所示，需要添加镜像点pi(i＝2,3
···
,n)(当n
→
∞时，可以得到精确解)。类似地，它在坐标轴上也是相同的镜像过程。涂层的存在足以改变应力分布。因此，对于涂层接触问题，我们采用类似的思路，选择半无限体中的接触载荷分布形式作为初始状态，涂层结构的应力场在n
→
∞时达到稳定。总之，当n
→
∞时，可以得到涂层内部的应力和位移分布。然后，将该方法与有限元方法进行了比较，包括表面和界面的变形比较，以及与现有分析方法的比较。
[0257]
涂层表面z＝h承受接触载荷
[0258][0259]
[0260]
其中，a是接触半径，f＝f
x
+ify是复库仑摩擦系数(i是虚数单位)，常数f
x
和fy是x和y方向的摩擦系数，可以通过实验确定。
[0261]
引入以下等式以简化符号：
[0262]
zj＝sjz、z
′j＝s
′jz、hj＝sjh、
[0263][0264][0265][0266]
(n＝1,2,
···
,∞；j＝0,1,2；k＝1,2,
···
,2n),
ꢀꢀꢀ
(3)
[0267]hn0
＝(2n-1)h0、h
nk
＝(2n-k)h1+(k-1)h2、
[0268][0269][0270][0271]
其中，n＝1,2,
···
,∞，k＝1,2,
···
,2n，sj是涂层0≤z≤h的特征值，s
′j是基体z≤0的特征值。
[0272]
一般解：在直角坐标(x,y,z)中，当平面xoy平行于各向同性平面时，三维横观各向同性材料的本构方程为
[0273][0274][0275][0276]
不考虑体力，力学平衡微分方程是
[0277][0278][0279]
在柱坐标(r,φ,z)中，当平面roφ平行于各向同性平面时，三维横观各向同性材料的本构方程为
[0280][0281]
[0282][0283]
不考虑体力，力学平衡微分方程包括以下公式：
[0284][0285][0286][0287]
其中，um和σm(τ
mn
)分别表示力学位移和应力的分量；c
ij
(i,j＝1,2,
…
,6)表示刚度系数。对于横观各向同性材料，有c
66
＝(c
11-c
12
)/2。
[0288]
把等式(c1)和(c3)代入等式(c2)和(c4)，我们有以下组合的一般解：
[0289][0290][0291][0292][0293]
以紧凑形式重写一般解：
[0294][0295][0296][0297][0298]
其中，其中，
[0299]
对于轴对称问题，和等式(c4)和(c3)的一般解包括以下公式：
[0300][0301]
[0302][0303][0304]
当s1≠s2，ψj满足以下调和方程包括以下公式：
[0305][0306]
zj＝sjz(j＝0,1,2)、
[0307][0308]
其中，特征值sj(j＝1,2)应满足re(sj)＞0和下面的方程式
[0309]
as
4-bs2+c＝0
ꢀꢀꢀ
(c11)
[0310]
和
[0311]
a＝c
33c44
、
[0312]
应该注意的是，等式(c8)中的一般解仅在s1≠s2时使用。
[0313]
1、在没有摩擦接触的情况下：
[0314]
1.1、没有摩擦接触的函数包括以下公式：
[0315][0316][0317]
其中，对于涂层，
[0318][0319]
其中，对于基层，
[0320][0321]
等式(a2.1)中的函数在等式(a3.1)中表示，等式(a2.2)中的函数在等式(a3.2)中表示。
[0322]
等式(a3.1)包括以下公式：
[0323][0324][0325]
[0326][0327][0328][0329][0330][0331][0332][0333][0334][0335]
其中，所述i和所述j和所述表示材料的坐标方向，所述c
ij
(i,j＝1,2,
…
,6)表示刚度系数，所述sj涂层四次多项式方程的特征值(0《z《h)，所述kj、所述mj和所述ωj均为材料特征值系数。
[0336]
等式(a3.2)包括以下等式：
[0337][0338][0339][0340]
[0341][0342]
1.2、一种基于柱面压头接触的涂层结构界面破坏预测方法，在没有摩擦接触的情况下，包括以下步骤：
[0343]
s101、在没有摩擦接触的情况下，横向各向同性涂层结构在圆柱坐标中考虑，涂层的厚度为h，涂层的范围为0≤z≤h，涂层与半无限基体完美结合，半无限基体的范围为z≤0，涂层的自由表面为z＝h，自由表面在光滑圆柱的接触荷载n的等式(5)为：
[0344][0345]
其中，r的范围为0≤r≤a，a是接触半径，pz是作用在锥凹形压头上的压痕载荷；
[0346]
s102、在涂层中，调和函数假定为以下等式(6)，等式(6)为：
[0347][0348]
等式(6)包括等式(7)，等式(7)包括以下公式：
[0349][0350][0351]
其中，n＝1,2,
···
,∞、j＝1,2、和a
njk
是待定系数，等式(7)包括等式(8)，等式(8)包括以下公式：
[0352][0353][0354]
其中，等式(8)包括等式(9)，等式(9)包括以下公式：
[0355][0356][0357][0358][0359]
s103、将等式(6)和等式(7)代入等式(c6)中得到等式(10)，等式(10)包括以下公式：
[0360]
[0361][0362][0363][0364][0365][0366]
其中，等式(10)包括等式(a3.1)，等式(c6)包含以下公式：
[0367][0368][0369][0370][0371]
和
[0372][0373]
其中，
[0374]
等式(c6)包括等式(c7)，等式(c7)包括以下公式：
[0375][0376][0377][0378]
和
[0379][0380]
和a
njk
均为待定系数；
[0381]
s104、在基体z≤0中，调和函数假定为以下等式(11)为：
[0382][0383]
等式(11)包括等式(12)，等式(12)的公式为：
[0384][0385]a′
njk
是待定系数，等式(12)包括等式(13)，等式(13)为：
[0386][0387]
等式13包括等式(14)，等式(14)包括以下公式：
[0388][0389][0390]
其中，z
′
njk
为坐标系数。
[0391]
s105、将等式(11)和等式(12)代入等式(c6)中得到等式(15)，等式(15)包括以下公式：
[0392][0393][0394][0395][0396][0397][0398]
其中，等式(15)包括等式(a3.2)。
[0399]
s106、在自由面z＝h上边界条件的等式(16)设定为以下公式：
[0400]
在0≤r≤a的范围内：
[0401]
在r＞a的范围内：
[0402][0403]
s107、表面z＝0上的界面连续性条件的等式(17)设定为以下公式：
[0404][0405][0406]
[0407][0408]
s108、根据等式(10)，将等式(16)分解，得到等式(18)和等式(19)：
[0409]
等式(18)包括以下公式：
[0410]
在0≤r≤a的范围内：
[0411]
在r＞a的范围内：
[0412][0413][0414]
等式(19)包括以下公式：
[0415][0416]
s109、根据等式(10)和等式(15)，将等式(17)分解得到等式(20)，等式(20)包括以下公式：
[0417][0418][0419][0420][0421]
s110、确定待定系数a
1jk
、a
′
1jk
、a
njk
、a
′
njk
和
[0422]
步骤s110中的a
1jk
、a
′
1jk
、a
njk
、a
′
njk
和的确定过程包括以下步骤：
[0423]
s1101、将等式(a3.1)代入等式(18)，得到等式(a4.1)，等式(a4.1)包括以下公式：
[0424][0425][0426][0427]
s1102、将等式(a3.1)代入等式(19)得到等式(a4.2)，等式(a4.2)包括以下公式：
[0428][0429][0430][0431][0432][0433][0434][0435]
其中，m＝1,2,
···
，2n-1)；
[0436]
s1103、将等式(a3.1)和等式(a3.2)代入等式(20)得到等式(a4.3)，等式(a4.3)包括以下公式：
[0437][0438][0439][0440][0441]
k＝1,2,
···
,2n；
[0442]
s1104、通过等式(a4.1)得到通过等式(a4.3)求解得到a
1jk
和通过等式(a4.2)求解得到通过等式(a4.3)求解得到a
njk
和a
′
njk
；等式(a4.3)包括8n个方程，为该等式的所有展开方程；通过等式(a4.2)求解得到等式(a4.2)包括4(n+1)个方程，为该等式的所有展开方程。
[0443]
2、存在摩擦接触的情况下：
[0444]
2.1、有摩擦接触的函数：
[0445][0446][0447]
其中，对于涂层包括以下公式：其中，对于涂层包括以下公式：
[0448]
其中，对于基体包括以下公式：
[0449][0450][0451]
等式(b2.1)中的函数在等式(b3.1)中表示，等式(b2.2)中的函数在等式(b3.2)中表示：
[0452]
等式(b3.1)包括以下公式：
[0453]
[0454][0455][0456][0457][0458][0459][0460][0461]
[0462][0463][0464][0465][0466]
等式(b3.2)包括以下公式：
[0467][0468][0469][0470][0471]
[0472][0473][0474][0475]
2.2、一种基于柱面压头接触的涂层结构界面破坏预测方法，在存在摩擦接触的情况下，包括以下步骤：
[0476]
s201、在横向各向同性涂层结构在柱面坐标中考虑，涂层的厚度为h，涂层的范围为0≤z≤h，涂层与半无限长基体z≤0完美结合，涂层的自由表面z＝h承受以下摩擦圆柱体接触载荷nf：
[0477][0478]
其中，r的范围为0≤r≤a，f＝f
x
+ify；
[0479]
s202、在涂层中，假定调和函数，调和函数的等式(22)包括以下公式：
[0480][0481][0482]
其中，等式(22)包括等式(23)，等式(23)包括以下公式：
[0483][0484][0485][0486][0487]
其中，等式(23)包括等式(24)，等式(24)包括以下公式：
[0488][0489][0490]
[0491][0492][0493][0494][0495][0496]
其中，b
n0
、b
njk
和是待定系数，等式(24)包括等式(25)，等式(25)包括以下公式：
[0497][0498][0499][0500][0501]
s203、将等式(22)和等式(23)代入等式(c6)得到等式(26)，等式(26)包括以下公式：
[0502][0503][0504][0505][0506][0507][0508]
等式(26)包括等式(b3.1)；
[0509]
s204、在基体中，假定调和函数的等式(27)包括以下形式：
[0510][0511][0512]
其中，等式(27)包括等式(28)，等式(28)包括以下公式：
[0513][0514][0515]
等式(28)包括等式(29)，等式(29)包括以下公式：
[0516][0517][0518][0519][0520]
其中，b
′
n0
和b
′
njk
是待定系数，等式(29)包括等式(30)，等式(30)包括以下公式：
[0521][0522][0523]
s205、将等式(27)和等式(28)代入等式(c6)，得到等式(31)，等式(31)包括以下公式：
[0524][0525][0526][0527][0528][0529][0530]
其中，等式(31)包括等式(b3.2)；
[0531]
s206、在自由面z＝h上的边界条件的等式(32)设定为以下公式：
[0532][0533]
在范围为0≤r≤a的等式为：
[0534]
在范围为r＞a的等式为：
[0535]
s207、表面z＝0上的界面连续性条件的等式(33)设定为以下公式：
[0536][0537][0538][0539][0540]
s208、根据等式(26)，将等式(32)分解得到等式(34)和等式(35)，等式(34)包括以下公式：
[0541]
在0≤r≤a范围内的公式为：
[0542]
在r＞a范围内的公式为：
[0543][0544]
等式(35)包括以下公式：
[0545][0546][0547]
s209、根据等式(26)和等式(31)，将等式(33)分解，得到等式(36)，等式(36)包括以下公式：
[0548][0549][0550][0551][0552]
s210、确定待定系数b
10
、b
′
10
、b
1jk
、b
′
1jk
、b
n0
、b
′
n0
、b
njk
、b
′
njk
、和
[0553]
步骤s210中的b
10
、b
′
10
、b
1jk
、b
′
1jk
、b
n0
、b
′
n0
、b
njk
、b
′
njk
、和的确定过程包括以下步骤：
[0554]
s2101、将等式(b3.1)代入等式(34)，得到等式(b4.1)，等式(b4.1)包括以下等式：
[0555][0556][0557]
[0558]
s2102、将等式(b3.1)代入等式(35)，得到等式(b4.2)，等式(b4.2)；
[0559][0560][0561][0562][0563][0564][0565][0566][0567]
n＝1,2,
···
,∞，m＝1,2,
···
,2n-1；
[0568]
s2103、将等式(b3.1)和等式(b3.2)代入等式(36)，得到等式(b4.3)，等式(b4.3)包括以下公式；
[0569][0570][0571][0572][0573][0574][0575]
n＝1,2,
···
,∞；；k＝1,2,
···
,2n；
[0576]
s2104、通过等式(b4.1)求得和通过等式(b4.3)求得b
10
，b
′
10
、b
1jk
和b
′
1jk
；通过等式(b4.2)求解得到和通过等式(b4.3)求解得到b
n0
，b
′
n0
，b
njk
和b
′
njk
；(b4.3)包括8n+2个方程，为该等式的所有展开方程；通过等式(b4.2)求解得到和等式b4.2包括8n+5个方程，为该等式的所有展开方程。
[0577]
最常见的涂层结构接触问题包括球面接触、圆锥接触和柱面接触。涂层结构的力学性能评估一直是力学和材料领域的重要课题，由于涂层厚度与基体厚度的比例太小，传统评估方法的偏差很难接受。压痕技术是涂层结构分析、测量和标准化应用的基础。本文的研究对象是涂层结构接触力学理论框架的系统构建工作之一
‑‑
圆柱接触。本文对涂层结构的柱面摩擦接触问题提出了一种精确有效的一般理论。推导了圆柱凸模摩擦接触下横观各向同性弹性涂层结构的三维精确解。提出了无摩擦接触和摩擦接触两种情况下的理论。与已有理论(本文降阶得到的)相比，数值计算显示了良好的收敛性、高精度、高效率和稳定
性。说明了有限元方法与该理论在应力奇异性分析中的不同之处，说明了该理论的有效性和适用性。该解析理论在边界应力奇异性分析中起着重要作用。有限元比较表明，解析理论在边界应力奇异性分析中发挥了重要作用，进一步证明了该理论的有效性和适用性。在数值分析中，给出了涂层厚度对界面应力的影响，给出了应力和位移的分布形式，研究了材料参数和涂层厚度对界面失效的影响。这篇文章包含了看似复杂的解析表达式，实际上都是关于初等函数的表达式。在计算机智能高度发展的时代，所提出的理论将成为界面失效问题分析和材料参数确定的基础，也为今后利用深度学习解决接触力学问题提供了高精度样本的基础。3、本实施例中存在的符号含义如下：
[0578]
[0579]
[0580][0581]
上述具体实施方式为本发明的优选实施例，并不能对本发明进行限定，其他的任何未背离本发明的技术方案而所做的改变或其它等效的置换方式，都包含在本发明的保护范围之内。