适配车基行驶状态监测系统的高速弯沉盆结果修正方法

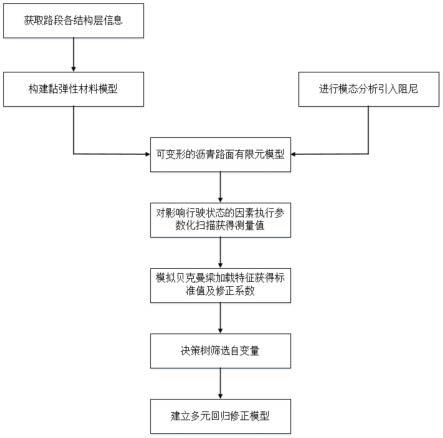
1.本发明属于路面结构强度评估领域，尤其涉及适配车基行驶状态监测系统的高速弯沉盆结果修正方法。


背景技术：

2.交通速度弯沉仪(tsd)的出现克服了传统测试方法低速、间断的问题，使得连续高效测量道路弯沉成为现实。交通速度弯沉仪对路面施加双轮单轴100kn的标准荷载，利用路面变形速度反演弯沉的方法，能够以最高120km/h的速度进行作业。交通速度弯沉仪布设有7个激光传感器，分别距车辆右后侧双轮组轮隙中心的距离10、20、30、60、90、150和350cm。
3.目前针对环境因素对交通速度弯沉仪影响的研究较为缺乏，仪器也多提倡在平直、交通状况较好的道路上使用。受场地与检测车辆操作的限制，交通速度弯沉仪现场测验的难度较大，试验结果的重复性较差。特别是路面形变量微小，现场试验无法保证测试条件的严格控制，难以对结果准确分析。而数值模拟方法由于其费用低、效率高，能够严格控制变量和快速精准地获取所需点位的弯沉盆形态与参数，因此更适用于交通速度弯沉仪的结果修正。此外不同于传统弯沉测量设备的冲击式加载或静态加载，高速弯沉仪加载特征为动态荷载，进行路面力学响应分析时有必要考虑面层材料的黏弹性效应。因此车辆行驶时车速、加减速、制动、上下坡等状态的经常性变化会对弯沉盆形态造成较明显的影响。多数有限元研究中仍采用的静态双圆荷载以及线弹性的路面模型，基于有限元的交通速度弯沉仪修正方法目前还有待完善。近年来车辆行驶状态监测系统发展迅速，这类车基系统能通过mems传感器、高精度六轴惯性导航模块对汽车的速度、加速度、三轴角速度进行数据采集监测，并通过蓝牙通信模块将数据发送至智能移动终端，为弯沉盆的修正提供充足、实时的车辆行驶信息。


技术实现要素：

4.本发明的目的在于：解决现有技术的问题，提供适配车基行驶状态监测系统的高速弯沉盆结果修正方法。
5.为实现上述目的，本发明提供如下技术方案：适配车基行驶状态监测系统的高速弯沉盆结果修正方法，包括以下步骤：
6.s1、获取面层材料试件进行动态模量实验，获取沥青路面有限元模型的结构参数与材料参数，构建关于黏弹性的路面模型；
7.s2、根据步骤s1获得的路面模型，模拟交通速度弯沉仪的加载特征，进行不同速度及路面因素作用下的仿真实验，计算相应弯沉盆指标作为修正路面模型的测量值y；
8.s3、根据步骤s1获得的路面模型模拟贝克曼梁的加载特征获取所需弯沉盆指标作为修正路面模型的标准值y0，之后根据步骤s2获得的修正路面模型的测量值y,进一步获得修正路面模型的修正系数ζ；
9.s4、根据步骤s2获得的修正路面模型的测量值，利用数据挖掘中的决策树算法筛
选环境条件影响因子，得到修正模型的影响因子；
10.s5、将步骤s3获得的修正系数ζ作为因变量，步骤s4获得的修正模型的影响因子作为自变量，构建修正系数的多项回归模型，
11.s6、进行数据采集监测，输入步骤s5构建的模型实现高速弯沉盆结果实时修正。
12.进一步地，所述步骤s1包括如下子步骤：
13.s1.1、采用旋转压实方法制备试件，进行动态模量实验获取动态模量和相位角，并转化为储能模量与损耗模量，如下式：
[0014][0015][0016]
ω＝2πf
[0017]
式中e
*
(ω)为复合模量；|e
*
(ω)|为动态模量；e
′
(ω)为储能模量；e
″
(ω)为损耗模量；为相位角；ω为角频率；f为荷载频率；
[0018]
s1.2、根据步骤s1.1获得的复合模量e
*
(ω)、相位角，进一步获得广义maxwell模型各分支对应的剪切模量prony级数序列与松弛时间以实现面层黏弹性材料的时间依赖性，广义maxwell模型中剪切模量g(t)、松弛模量e(t)、储存模量e
′
(ω)和损耗模量e
″
(ω)三者的关系如下：
[0019][0020][0021][0022][0023]
其中，e∞为平衡模量；em为广义maxwell模型各分支单元对应的弹性模量；g∞为平衡剪切模量；gm为广义maxwell模型各分支单元对应的剪切模量；τm为广义maxwell模型各分支单元对应的松弛时间；m为广义maxwell模型的分支数；p0为材料泊松比；
[0024]
s1.3、面层黏弹性材料的温度依赖性如下式：
[0025][0026]
其中，a
t
为移位因子，被定义为不同测试温度下的动态模量曲线与参考温度t0的偏移值；c1，c2为回归系数，绘制log(a
t
)与t-t0的曲线即可拟合得出；
[0027]
s1.4，弯沉盆形态面层和基层的粘弹性阻尼比δi如下式：
[0028]
[0029]
其中，ωi为模态i的固有角频率；α、β均为比例系数，ω1、ω2分别为模态分析第一、第二阶段的固有频率；
[0030]
s1.5、预设结构参数：路面模型长度、道路两侧至边界的距离、地基厚度，服从圣维南原理，道路纵向两个断面的x方向位移被约束，道路横向两断面y方向位移被约束，底面全部约束，路面边界为完全自由边界，各结构层之间的接触设置为完全连续，并根据材料参数：杨氏模量、泊松比、密度、黏弹性材料参数、粘性阻尼比黏弹性的路面模型。
[0031]
进一步地，所述步骤s2包括如下子步骤：
[0032]
s2.1、采用匀变速模拟汽车的加速与制动行为如下式：
[0033]
v＝v0+at
[0034][0035]
车辆做匀加速运动时，每个荷载步的加载时间为：
[0036][0037]
车辆做匀减速运动时，每个荷载步的加载时间为：
[0038][0039]
其中，a为车辆加速度，a＝0时，车辆即为匀速状态；g为重力加速度，g＝9.8m/s2；ti为第i个时间步长；l为第i个距离步长；
[0040]
s2.2，采用简谐振动模型以振动的振幅、频率及周期性来描述交通速度弯沉仪的加载特征，荷载fz垂直于路面，方向向下：
[0041]fz
＝f0+f1sin(wt)
[0042]
f1＝m0cw2[0043][0044]
其中，f0为车辆静载，采用非均布的轮胎胎迹，f1为振动荷载幅值；m0为车辆模型簧下质量，c为几何不平整矢高，w为振动圆频率，v为车辆运行速度，l为几何曲线波长；
[0045]
s2.3、匀速行驶时路面仍受摩擦力的作用，故在轮迹区域施加方向为正的纵向水平力：
[0046]fy
＝ψfz[0047]
其中，fy为路面所受纵向水平力；ψ为摩擦系数取0.01至0.02；fz为交通速度弯沉仪施加的垂直向荷载；
[0048]
s2.4、根据车辆纵坡行驶的工况，计算路面垂直方向受力如下式：
[0049]fz
＝i2f
[0050]
其中，i2为纵坡夹角余弦值，i1为道路纵坡坡度，i1等同于纵坡夹角正弦值；
[0051]
计算车辆在纵坡上行驶路面与车辆接触区域纵向受力fy的表达式如下式：
[0052]
[0053]
其中，正号为方向与行驶方向相同，fi为加速或减速状态带来的惯性力，路面在车辆行进方向仍受摩擦力fj的作用，fj＝ψi2f，ψ为摩擦系数；fh为坡度阻力，fh＝i1f，上坡时符号取负，下坡时符号取正；
[0054]
s2.5、计算路面与车辆接触区域垂直于行车方向的受力表达式如下式：
[0055]fx
＝ffz[0056]
其中，f为离心力系数，
[0057]
s2.6，在起点选择一组单元，在其上施加面荷载，持续时间由单元长l及行车速度决定，然后删除面荷载，以轮载向前移动一排单元的方式构成下一组加载单元，在其上施加面荷载，持续时间不变，直至选择最后一组单元，并施加最后一个轮载至循环结束；
[0058]
s2.7，通过参数化扫描模拟车辆不同的行驶状态，包括上坡、下坡、加速、减速、转弯，每个影响因素取预设个值进行所有组合的扫描，得到弯沉指标测试值y，用于修正模型的回归；
[0059]
s2.8，对模型中央对应的时间步进行瞬态分析，测试值包括弯沉指标d0、d
0-d
20
、d
20-d
60
、d
60-d
120
、d
120
，分别表征路面整体、面层、基层、底基层、地基的强度，其值越小则说明承载能力越好，其中d0为加载中心弯沉值，d
20
、d
60
、d
120
为距加载中心处前方20、60、120mm处的弯沉大小。
[0060]
进一步地，所述步骤s3具体为：在面层为黏弹性材料的条件下模拟贝克曼梁的检测，加载区域为预设半径的双圆均布荷载，预设区域内垂直荷载大小，摩擦力基于步骤s2.3，并且圆心间距、移动速度、移动距离设置为预设值，采用阶跃加载加载方式，预设瞬态分析总时长，在某一秒提取各弯沉指标作为标准值y0，按照下式定义修正系数ζ：
[0061]
y0＝ζy。
[0062]
进一步地，所述步骤s4具体为：以步骤2.7获取的弯沉指标测试值y作为因变量，各影响因素作为自变量采用cart算法进行决策树分析，以决策树的r2增益作为控制过拟合的指标，根据预设验证比例，求解最佳拆分数，通过对自变量的贡献排序筛选出影响较大的环境条件影响因子。
[0063]
进一步地，所述步骤s5包括以下子步骤：
[0064]
s5.1、基于步骤s4获得的决策树分析结果，筛选其中影响较大的m个环境条件作为因子建立二次回归模型，按如下公式建立修正模型：
[0065][0066]
其中，β为待求解的回归系数；x为影响因素；
[0067]
s5.2、根据拟合结果的效应汇总进行筛选，筛选指标包括相关系数、p值、均方根误差，其中均方根误差与相关系数衡量拟合优度，p值用于筛选模型各项的显著性，根据预设p值，获得最终的环境影响因素修正模型。
[0068]
本发明采用以上技术方案，与现有技术相比的有益效果如下：本发明公开的基于有限元建模、数据挖掘、回归分析的弯沉结果修正方法，用于交通速度弯沉仪在不同环境因素影响下测得的弯沉盆指标修正。基于考虑黏弹性和非均布移动荷载的有限元模型，能够
有效模拟交通速度弯沉仪测试时的行驶状态，表征沥青路面弯沉盆指标在不同工况下的变化规律，有助于量化评估车辆不同行驶状态的影响；同时利用本发明提出的回归修正模型，能够为交通速度弯沉仪的测量结果优化提供理论参考，提高设备测量的准确度。
附图说明
[0069]
图1为本发明的技术流程图。
[0070]
图2为本发明的标准行驶速度下垂直方向荷载简谐波示意图。
[0071]
图3为本发明的交通速度弯沉仪轮迹示意图。
[0072]
图4为本发明的阶跃加载示意图。
具体实施方式
[0073]
为了更了解本发明的技术内容，特举具体实施例并配合所附图式说明如下。
[0074]
在本发明中参照附图来描述本发明的各方面，附图中示出了许多说明性实施例。本发明的实施例不局限于附图所述。应当理解，本发明通过上面介绍的多种构思和实施例，以及下面详细描述的构思和实施方式中的任意一种来实现，这是因为本发明所公开的构思和实施例并不限于任何实施方式。另外，本发明公开的一些方面可以单独使用，或者与本发明公开的其他方面的任何适当组合来使用。
[0075]
如图1所示，本发明的流程图，执行以下步骤：
[0076]
s1、获取面层材料试件进行动态模量实验，获取沥青路面有限元模型的结构参数与材料参数，构建考虑黏弹性的路面模型，动态模量实验可取自现场的钻取芯样，也可取自室内成型的试样。动态模量实验可通过旋转压实仪和基本性能试验仪(spt)直接获得沥青混合料的动态模量主曲线。动态模量试验结果中的复数模量和相位角可转化为松弛模量。路面模型的黏弹性的时间依赖性利用广义maxwell模型实现，温度依赖性通过使用williams-landel-ferry(wlf)方程来获取。
[0077]
面层材料为sma-13，沥青层厚16cm，基层厚38cm，底基层厚20cm，地基厚5m，路段材料、面层黏弹性材料剪切模量参数、wlf方程相关参数、rayleigh阻尼相关参数等信息如下表所示：
[0078]
表1路面结构材料参数表
[0079][0080]
表2面层材料剪切模量参数表
[0081][0082][0083]
表3wlf方程相关参数
[0084]
类型t
ref
(℃)c1c2sma-1321.110.9116.3
[0085]
表4rayleigh阻尼相关参数
[0086]
面层类型特征频率1特征频率2αβsma-1316.977hz17.759hz0.8679598770.002878858
[0087]
步骤s1具体为以下步骤s1.1至步骤s1.5:
[0088]
s1.1，依据测试路段设计书提供的面层材料级配信息，参考试验规程aashto tp62-03，采用旋转压实方法制备试件，并使用superpave基本性能试验机(spt)进行动态模量试验获取动态模量和相位角，并通过关系式转化为储能模量与损耗模量，实验过程中设置的加载温度应从低温向高温过渡，加载频率由高频到低频过渡。
[0089][0090][0091]
ω＝2πf
[0092]
其中，e
*
(ω)为复合模量，|e
*
(ω)|为动态模量，e
′
(ω)为储存模量，e
″
(ω)为损耗模量，为相位角，ω为角频率，f为荷载频率。
[0093]
s1.2，将试验所获取的复数模量及相位角带入常用的转化公式，获得广义maxwell模型各分支对应的剪切模量prony级数序列与松弛时间以实现面层黏弹性材料的时间依赖
性，广义maxwell模型中剪切模量g(t)、松弛模量e(t)、储存模量e
′
(ω)和损耗模量e
″
(ω)三者的关系式为：
[0094][0095][0096][0097][0098]
其中，e∞为平衡模量；em为广义maxwell模型各分支单元对应的弹性模量；g∞为平衡剪切模量；gm为广义maxwell模型各分支单元对应的剪切模量；τm为广义maxwell模型各分支单元对应的松弛时间；m为广义maxwell模型的分支数；p0为材料泊松比。
[0099]
s1.3，面层黏弹性材料的温度依赖性由willians-landel-ferry(wlf)方程体现，wlf方程如下式所示：
[0100][0101]
其中，a
t
为移位因子，被定义为不同测试温度下的动态模量曲线与参考温度t0的偏移值；c1，c2为回归系数，绘制log(a
t
)与t-t0的曲线即可拟合得出。
[0102]
s1.4，弯沉盆形态受到惯性阻尼的影响，基层与底基层视为弹性不设置阻尼，面层与地基的阻尼比设置为0.05，对于面层和基层可引入rayleigh阻尼进行模拟，
[0103][0104]
其中，ωi为模态i的固有角频率，可通过模态分析来确定；δi为粘性阻尼比；α、β均为比例系数，将模态分析的前两阶固有频率ω1、ω2带入联立方程式，即可求得。
[0105]
s1.5，建立路面模型，为防止边界效应影响，模型长度设置为20m，道路两侧至边界的距离应大于2.5m，地基厚度应大于5m，模型边界条件服从圣维南原理，道路纵向两个断面的x方向位移被约束，道路横向两断面y方向位移被约束，底面全部约束，路面边界为完全自由边界，各结构层之间的接触设置为完全连续，输入各层材料参数，包括杨氏模量、泊松比、密度、黏弹性材料相关参数、阻尼比相关参数。
[0106]
s2、基于步骤1所建立的道路模型，模拟交通速度弯沉仪的加载特征，进行不同车速、加速度、纵坡坡度、离心力系数等因素作用下的仿真实验，每个影响因素取3个值进行所有组合的参数化扫描，执行参数化扫描考虑车辆行驶的实际状况，上坡与加速组合，下坡与减速组合，加速度为0时即为匀速上下坡，实现对复杂工况的模拟。步骤2中的车辆轮迹与静态胎压数据来自实际测量，荷载非均匀分布。
[0107]
计算弯沉盆指标d0作为修正模型的测量值y，单位为0.01mm，参数设定如表5所示。
[0108]
表5车辆行驶状态参数
[0109]
车速/kph6070100上坡坡度0.020.040.08下坡坡度0.020.040.08
离心力系数0.10.20.4启动加速度/(m/s2)468制动加速度/(m/s2)468
[0110]
具体为以下步骤s2.1至步骤s2.8:
[0111]
s2.1、模拟实现汽车不同的运动状态，采用匀变速模拟汽车的加速与制动行为:
[0112]
v＝v0+at
[0113][0114]
车辆做匀加速运动时，每个荷载步的加载时间为:
[0115][0116]
车辆做匀减速运动时，每个荷载步的加载时间为:
[0117][0118]
式中，a为车辆加速度，a＝0时，车辆即为匀速状态；g为重力加速度，g＝9.8m/s2；ti为第i个时间步长；l为第i个距离步长。
[0119]
s2.2，采用简谐振动模型以振动的振幅、频率及周期性来描述交通速度弯沉仪的加载特征如图2所示，为反映路面不平整度、车辆振动及车路耦合等因素的影响，垂直方向的车辆荷载fz采用采用一系列幅值不等的正弦波荷载作为车辆动载和路面结构动力响应分析的前提。
[0120]
荷载fz垂直于路面，方向向下：
[0121]fz
＝f0+f1sin(wt)
[0122]
f1＝m0cw2[0123][0124]
式中，f0为车辆静载，采用非均布的轮胎胎迹，如图2所示；f1为振动荷载幅值；m0为车辆模型簧下质量,重型卡车取值1200n
·
s2/m；c为几何不平整矢高，取c＝2mm；w为振动圆频率；v为车辆运行速度，交通速度弯沉仪行驶的标准速度一般为70km/h；l为几何曲线波长，鉴于交通速度弯沉仪最远端的激光器设置在3.5m处，将l取值为7m.
[0125]
s2.3，匀速行驶时路面仍受摩擦力的作用，故在轮迹区域施加方向为正的纵向水平力。
[0126]fy
＝ψfz[0127]
其中，fy为路面所受纵向水平力；ψ为摩擦系数取0.01至0.02；fz为交通速度弯沉仪施加的垂直向荷载。
[0128]
s2.4，考虑测试车辆纵坡行驶的工况，路面垂直方向受力为：
[0129]fz
＝i2f
[0130]
其中，i2为纵坡夹角余弦值，i1为道路纵坡坡度，一般直接将i1等同于纵坡夹角正弦值。
[0131]
测试车辆在纵坡上行驶时，路面与车辆接触区域纵向受力fy的表达式如下所示，其中正号意味方向与行驶方向相同：
[0132][0133]
其中，fi为加速或减速状态带来的惯性力，路面在车辆行进方向仍受摩擦力fj的作用，fj＝ψi2f，摩擦系数ψ取值范围为0.01到0.02；fh为坡度阻力，fh＝i1f，上坡时符号取负，下坡时符号取正。
[0134]
s2.5，考虑测量车辆在平坡进行转弯时，受到离心力作用，故路面与车辆接触区域垂直于行车方向的受力表达式为：
[0135]fx
＝ffz[0136]
其中，f为离心力系数，
[0137]
s2.6，在起点选择一组单元，在其上施加面荷载，持续时间由单元长l及行车速度决定，l建议取值在1-2cm；然后删除面荷载，轮载向前移动一排单元，构成另外一组加载单元，并在其上施加面荷载，持续时间不变，依次类推，直至选择最后一组单元，并施加最后一个轮载至循环结束，这样就相当于车辆以预设的速度向前行驶，荷载移动总路程为14m，研究点位为路程中心处。
[0138]
s2.7，通过参数化扫描模拟车辆不同的行驶状态，包括上坡、下坡、加速、减速、转弯，每个影响因素取3个值进行所有组合的扫描，得到弯沉指标测试值y，用于修正模型的回归。
[0139]
s2.8，对模型中央对应的时间步进行瞬态分析，测试值包括弯沉指标d0、d
0-d
20
、d
20-d
60
、d
60-d
120
、d
120
，分别表征路面整体、面层、基层、底基层、地基的强度，其值越小则说明承载能力越好，其中d0为加载中心弯沉值，d
20
、d
60
、d
120
为距加载中心处前方20、60、120mm处的弯沉大小。
[0140]
s3、基于步骤1中所建立的路面模型，模拟贝克曼梁的加载特征获取所需弯沉盆指标作为修正模型的标准值y0，标准值y0与步骤s2获取的各工况下测量值y的比被定义为修正系数ζ。具体为:在面层为黏弹性材料的条件下模拟贝克曼梁的检测，加载区域为半径为10.65cm的双圆均布荷载，区域内垂直荷载大小设置为0.7mpa，摩擦力设置过程与步骤2.3相同，圆心间距设置为29.9cm，移动速度为5km/h，移动距离14m，如图4所示加载方式采用阶跃加载，瞬态分析总时长为10.08s，在5.04s提取各弯沉指标作为标准值y0，按照下式定义修正系数ζ：
[0141]
y0＝ζy。
[0142]
s4、基于测量值y，利用数据挖掘中的决策树算法筛选影响较大的环境条件影响因子。具体为：以步骤2.7获取的弯沉指标测试值y作为因变量，各影响因素作为自变量采用cart算法进行决策树分析，以决策树的r2增益作为控制过拟合的指标，设置0.3的验证比例，求解最佳拆分数，贡献最大的三项分别为制动加速度、车速、启动加速度，对应的贡献率分别为0.36、0.34、0.26，得到修正模型的影响较大的环境条件影响因子x1、x2、x3。
[0143]
s5、将修正系数ζ作为因变量，影响因子x1、x2、x3作为自变量，构建修正系数的多项回归模型，以显著性为依据保留p《0.05的项，最终得到的修正模型如下，均方根误差为
0.68，相关系数为0.79。
[0144][0145]
包括以下步骤s5.1至s5.2：
[0146]
s5.1基于步骤4获得的决策树分析结果，筛选其中影响较大的m(m《3)个环境条件作为因子建立二次回归模型，修正模型表达式以及如下：
[0147][0148]
其中，β为待求解的回归系数；x为影响因素。
[0149]
s5.2根据拟合结果的效应汇总进行筛选，筛选指标包括相关系数、p值、均方根误差，其中均方根误差与相关系数衡量拟合优度，p值用于筛选模型各项的显著性，对p《0.05的项予以保留，获得最终的环境影响因素修正模型。
[0150]
虽然本发明已以较佳实施例阐述如上，然其并非用以限定本发明。本发明所属技术领域中具有通常知识者，在不脱离本发明的精神和范围内，当可作各种的更动与润饰。因此，本发明的保护范围当视权利要求书所界定者为准。