一种基于阻力系数修正的固液两相流数值计算方法

1.本技术涉及流体机械工程技术领域，特别涉及一种基于阻力系数修正的固液两相流数值计算方法。


背景技术：

2.在流体机械泥沙磨损预测过程中，固液两相流计算的准确性对磨损预测起决定性作用，阻力作为固液间动量传递的关键因素，其准确建模对两相流计算至关重要。
3.相关技术中，流体机械固液两相流计算，多基于wen-yu模型或一般球形阻力模型计算阻力，模型中均未考虑湍流因素对阻力的影响，而已有研究表明湍流会显著增加颗粒阻力，流体机械系统中固液两相流的湍流强度高，对泥沙阻力系数的影响显著。其中，在较低浓度固液两相流计算中，相关技术对含沙阻力系数修正多从wen-yu模型进行改进，其适用范围有限，且对高湍流条件下的固液两相流流动计算的准确性有待提高。


技术实现要素：

4.本技术提供一种基于阻力系数修正的固液两相流数值计算方法，以解决相关技术中，基于wen-yu模型改进，在较低浓度固液两相流计算中对含沙阻力系数修正的适用范围有限，且对高湍流条件下的固液两相流流动计算的准确性较低的技术问题。
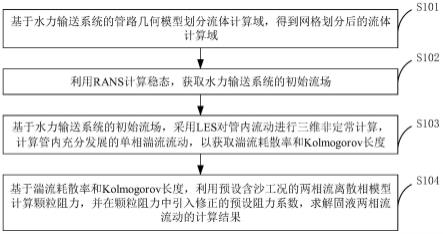
5.本技术实施例提供一种基于阻力系数修正的固液两相流数值计算方法，包括以下步骤：基于水力输送系统的管路几何模型划分流体计算域，得到网格划分后的流体计算域；利用rans计算稳态，获取所述水力输送系统的初始流场；基于所述水力输送系统的初始流场，采用les对管内流动进行三维非定常计算，计算管内充分发展的单相湍流流动，以获取湍流耗散率和kolmogorov长度；基于所述湍流耗散率和kolmogorov长度，利用预设含沙工况的两相流离散相模型计算颗粒阻力，并在所述颗粒阻力中引入修正的预设阻力系数，求解固液两相流流动的计算结果。
6.可选地，在本技术的一个实施例中，网格划分及时间步长确定需满足收敛条件判断数cfl，公式为：
[0007][0008]
其中，u为主流区速度，δx为网格尺寸，δt为时间步长。
[0009]
可选地，在本技术的一个实施例中，所述获取湍流耗散率和kolmogorov长度，包括：基于所述单相湍流流动，求解统计时间段内多个瞬时速度，得到所述统计时间段的平均速度；根据所述多个瞬时速度和所述平均速度计算脉动速度，并基于所述脉动速度利用预设公式计算变形率张量、所述湍流耗散率和所述kolmogorov长度。
[0010]
可选地，在本技术的一个实施例中，所述预设公式为：
[0011]
[0012][0013][0014]
其中，u
′
为脉冲速度，v为液体的运动粘度，ε为湍流耗散率，s
′
ij
为变形率张量，λ为kolmogorov长度。
[0015]
可选地，在本技术的一个实施例中，所述预设含沙工况的颗粒阻力计算公式为：
[0016][0017][0018]
其中，u
p
为颗粒速度，re
p
为颗粒雷诺数，ρ
p
为颗粒密度，d
p
为颗粒直径，下标p表示颗粒，下标f表示液体，uf为液体速度，μf为液体动力粘度，ρf为液体密度，为颗粒阻力，c
d,turb
为修正的预设阻力系数。
[0019]
本技术实施例可以采用les及周期性边界条件获取充分发展的单相湍流流动，基于les获取的流动参数计算湍流耗散率及kolmogorov长度，建立含沙工况下修正阻力系数的两相流离散相模型，引入包含kolmogorov长度及颗粒粒径的函数，以考虑自由湍流对颗粒阻力的影响，计算两相流流动，求解固液两相流流动的计算结果，可以适用于流体机械中高雷诺数强湍流流体含沙工况，可准确模拟流体机械中固液两相的速度，数值计算结果准确度较高。由此，解决了相关技术中，基于wen-yu模型改进，在较低浓度固液两相流计算中对含沙阻力系数修正的适用范围有限，且对高湍流条件下的固液两相流流动计算的准确性较低的技术问题。
[0020]
本技术附加的方面和优点将在下面的描述中部分给出，部分将从下面的描述中变得明显，或通过本技术的实践了解到。
附图说明
[0021]
本技术上述的和/或附加的方面和优点从下面结合附图对实施例的描述中将变得明显和容易理解，其中：
[0022]
图1为根据本技术实施例提供的一种基于阻力系数修正的固液两相流数值计算方法的流程图；
[0023]
图2为根据本技术一个实施例的一种基于阻力系数修正的固液两相流数值计算方法的流程图；
[0024]
图3为根据本技术一个实施例的一种基于阻力系数修正的固液两相流数值计算方法的计算域局部网格示意图；
[0025]
图4为根据本技术一个实施例的一种基于阻力系数修正的固液两相流数值计算方法的计算域流动情况及边界条件示意图；
[0026]
图5为根据本技术一个实施例的一种基于阻力系数修正的固液两相流数值计算方法的主流脉动速度沿管路半径方向变化曲线示意图。
具体实施方式
[0027]
下面详细描述本技术的实施例，所述实施例的示例在附图中示出，其中自始至终相同或类似的标号表示相同或类似的元件或具有相同或类似功能的元件。下面通过参考附图描述的实施例是示例性的，旨在用于解释本技术，而不能理解为对本技术的限制。
[0028]
下面参考附图描述本技术实施例的一种基于阻力系数修正的固液两相流数值计算方法。针对上述背景技术中心提到的相关技术中，基于wen-yu模型改进，在较低浓度固液两相流计算中对含沙阻力系数修正的适用范围有限，且对高湍流条件下的固液两相流流动计算的准确性较低的技术问题，本技术提供了一种基于阻力系数修正的固液两相流数值计算方法，在该方法中，可以采用les及周期性边界条件获取充分发展的单相湍流流动，基于les获取的流动参数计算湍流耗散率及kolmogorov长度，建立含沙工况下修正阻力系数的两相流离散相模型，引入包含kolmogorov长度及颗粒粒径的函数，以考虑自由湍流对颗粒阻力的影响，计算两相流流动，求解固液两相流流动的计算结果，可以适用于流体机械中高雷诺数强湍流流体含沙工况，可准确模拟流体机械中固液两相的速度，数值计算结果准确度较高。由此，解决了相关技术中，基于wen-yu模型改进，在较低浓度固液两相流计算中对含沙阻力系数修正的适用范围有限，且对高湍流条件下的固液两相流流动计算的准确性较低的技术问题。
[0029]
具体而言，图1为本技术实施例所提供的一种基于阻力系数修正的固液两相流数值计算方法的流程示意图。
[0030]
如图1所示，一种基于阻力系数修正的固液两相流数值计算方法包括以下步骤：
[0031]
在步骤s101中，基于水力输送系统的管路几何模型划分流体计算域，得到网格划分后的流体计算域。
[0032]
在实际执行过程中，本技术实施例可以根据水力输送系统中部件实际尺寸，建立计算管路几何模型，并采用六面体结构化网格对管路模型进行网格划分，例如，第一层网格高度满足y+≈1，网格增长比例1.1，网格质量大于0.5。
[0033]
可选地，在本技术的一个实施例中，网格划分及时间步长确定需满足收敛条件判断数cfl，公式为：
[0034][0035]
其中，u为主流区速度，δx为网格尺寸，δt为时间步长。
[0036]
在实际执行过程中，本技术实施例可以控制cfl数小于1。
[0037]
在步骤s102中，利用rans计算稳态，获取水力输送系统的初始流场。
[0038]
作为一种可能实现的方式，本技术实施例可以利用rans计算稳态获得初始流场，采用sst k-ω湍流模型，设置区域内流体为液相水，管路两端设置为周期性边界条件，管路壁面为无滑移壁面，从而计算稳定后利用tui命令给速度添加脉动，获得瞬态计算的初始流场。
[0039]
在步骤s103中，基于水力输送系统的初始流场，采用les对管内流动进行三维非定常计算，计算管内充分发展的单相湍流流动，以获取湍流耗散率和kolmogorov长度。
[0040]
在一些实施例中，本技术实施例可以计算获得的水利输送系统的初始流场，采用les对管内流动进行三维非定常计算，计算管内充分发展的单相湍流流动，求解得到瞬时速
度，并进一步获得平均速度和脉动速度，以计算变形率张量、湍流耗散率及kolmogorov长度。
[0041]
具体地，本技术实施例可以采用les对管内流动进行三维非定常计算，本技术实施例可以基于网格划分及时间步长确定需满足收敛条件判断数cfl，通过控制cfl数约为0.5估算时间步长，在每一步中保证残差下降2个数量级，以获取管内充分发展的单相湍流流动。
[0042]
本技术实施例可以计算2～3个流动周期以获取充分发展的湍流，随后达到统计上的稳定状态，并且在达到统计稳定状态之前，不收集任何不稳定的统计数据。
[0043]
可选地，在本技术的一个实施例中，获取湍流耗散率和kolmogorov长度，包括：基于单相湍流流动，求解统计时间段内多个瞬时速度，得到统计时间段的平均速度；根据多个瞬时速度和平均速度计算脉动速度，并基于脉动速度利用预设公式计算变形率张量、湍流耗散率和kolmogorov长度。
[0044]
在实际执行过程中，本技术实施例可以对流动进行求解得到瞬时速度u，在统计时间段内累加求和并平均获得平均速度后计算得到脉动速度利用预设公式计算变形率张量s
′
ij
、湍流耗散率ε及kolmogorov长度λ。
[0045]
可选地，在本技术的一个实施例中，预设公式为：
[0046][0047][0048][0049]
其中，
′
为脉冲速度，v为液体的运动粘度，ε为湍流耗散率，s
′
ij
为变形率张量，λ为kolmogorov长度。
[0050]
进一步地，i、j的取值可以为1、2、3。
[0051]
在步骤s104中，基于湍流耗散率和kolmogorov长度，利用预设含沙工况的两相流离散相模型计算颗粒阻力，并在颗粒阻力中引入修正的预设阻力系数，求解固液两相流流动的计算结果。
[0052]
作为一种可能实现的方式，本技术实施例可以利用预先建立的含沙工况的两相流离散相模型，基于湍流耗散率和kolmogorov长度计算颗粒阻力，并在颗粒阻力中引入修正的预设阻力系数，求解固液两相流流动的计算结果，本技术实施例可以在达到统计稳定状态后，切换采样时间间隔，再计算2个流动周期并采集两相流非稳态数据。
[0053]
可选地，在本技术的一个实施例中，颗粒阻力计算公式为：
[0054][0055][0056]
其中，u
p
为颗粒速度，re
p
为颗粒雷诺数，ρ
p
为颗粒密度，d
p
为颗粒直径，下标p表示颗粒，下标f表示液体，uf为液体速度，μf为液体动力粘度，ρf为液体密度，为颗粒阻
力，c
d,turb
为修正的预设阻力系数。
[0057]
在实际执行过程中，离散相颗粒可以在拉格朗日坐标系下求解，本技术实施例可以通过对颗粒作用力微分方程进行积分追踪颗粒运动轨迹，用随机游走模型计算液体湍流引起的粒子扩散，固体颗粒在固液流场中运动时受到阻力、重力引起的浮力、压力梯度力和虚拟质量力，可以表示为：
[0058][0059]
其中，
[0060][0061][0062][0063][0064]
其中，fd为阻力，fb为重力引起的浮力，f
vm
为虚质量力，f
p
为压力梯度力，f为其他力；m
p
为颗粒质量，u
p
为颗粒速度，cd为阻力系数，re
p
为颗粒雷诺数，ρ
p
为颗粒密度，ρ为流体质量，d
p
为颗粒直径，u为流体速度，c
vm
为虚拟质量系数，取0.5；下标p表示颗粒。
[0065]
此外，在液相动量方程中，可以通过体积力源项计算颗粒对流体的动量传递作用，以考虑颗粒对流体的作用。
[0066]
本技术实施例可以在计算阻力fd时，为考虑湍流强度对颗粒阻力的影响，在基于两相滑移速度的颗粒阻力系数中引入包含kolmogorov长度及颗粒粒径的函数：
[0067][0068][0069]
则得到改进后的阻力模型可以为：
[0070][0071][0072][0073]
基于上述方法，本技术实施例可以实现流体机械内两相流流动的数值模拟，以揭示颗粒在流体机械内运动规律，从而为流体机械磨损研究奠定理论基础。
[0074]
结合图2至图5所示，以一个实施例对本技术实施例的一种基于阻力系数修正的固液两相流数值计算方法进行详细阐述。
[0075]
在实施例中，可以以国外公开的直管系统内固液两相流为例，其中，管路内径77.22mm，雷诺数2
×
105，颗粒直径1mm，颗粒体积浓度0.7％，流动方向为自下而上。
[0076]
在实际执行过程中，本技术实施例可以基于les求解得到的流动参数计算kolmogorov长度，通过引入kolmogorov长度与颗粒粒径间的关系函数，考虑湍流对颗粒阻力的影响，得到改进后的阻力模型计算固液两相流。
[0077]
具体而言，如图2所示，本技术实施例可以包括
[0078]
步骤s201：对流体计算域进行网格划分。如图3所示，本技术实施例可以根据水力输送系统中部件实际尺寸，建立管路内径77.22mm、总长500mm的直管几何模型，并采用六面体结构化网格对管路模型进行网格划分，第一层网格高度满足y+≈1，网格增长比例1.1，网格质量大于0.5。
[0079]
步骤s202：利用rans获取初始流场。如图4所示，本技术实施例可以在利用les计算瞬态管流前，利用rans计算稳态获得初始流场，采用sst k-ω湍流模型，设置区域内流体为液相水，管路两端设置为周期性边界条件，管路壁面为无滑移壁面，并计算稳定后利用tui命令给速度添加脉动，获得瞬态计算的初始流场。
[0080]
步骤s203：采用les获取充分发展的湍流场。本技术实施例可以采用les对管内流动进行三维非定常计算，通过控制cfl数约为0.5估算时间步长，在每一步中保证残差下降2个数量级，以获取管内充分发展的单相湍流流动：
[0081][0082]
其中，u为主流区速度，δx为网格尺寸，δt为时间步长。
[0083]
本技术实施例可以计算2个流动周期以获取充分发展的湍流，随后达到统计上的稳定状态，且在达到统计稳定状态之前，不收集任何不稳定的统计数据。
[0084]
步骤s204：在les计算中获取湍流耗散率ε及kolmogorov长度。本技术实施例可以对流动进行求解得到瞬时速度u，在统计时间段内累加求和并平均获得平均速度后计算得到脉动速度利用如下公式计算变形率张量s
′
ij
、湍流耗散率ε及kolmogorov长度λ：
[0085][0086][0087][0088]
其中，v为液体的运动粘度，i、j的取值可以为1、2、3。
[0089]
步骤s205：建立含沙工况的两相流离散相模型。在实际执行过程中，离散相颗粒可以在拉格朗日坐标系下求解，本技术实施例可以通过对颗粒作用力微分方程进行积分追踪颗粒运动轨迹，用随机游走模型计算液体湍流引起的粒子扩散，固体颗粒在固液流场中运动时受到阻力、重力引起的浮力、压力梯度力和虚拟质量力，可以表示为：
[0090][0091]
其中，
[0092][0093][0094][0095][0096]
其中，fd为阻力，fb为重力引起的浮力，f
vm
为虚质量力，f
p
为压力梯度力，f为其他力；m
p
为颗粒质量，u
p
为颗粒速度，cd为阻力系数，re
p
为颗粒雷诺数，ρ
p
为颗粒密度，ρ为流体质量，d
p
为颗粒直径，u为流体速度，c
vm
为虚拟质量系数，取0.5；下标p表示颗粒。
[0097]
此外，在液相动量方程中，可以通过体积力源项计算颗粒对流体的动量传递作用，以考虑颗粒对流体的作用。
[0098]
步骤s206：在颗粒阻力中引入修正的阻力系数。本技术实施例可以在计算阻力fd时，为考虑湍流强度对颗粒阻力的影响，在基于两相滑移速度的颗粒阻力系数中引入包含kolmogorov长度及颗粒粒径的函数：
[0099][0100][0101]
则得到改进后的阻力模型可以为：
[0102][0103][0104][0105]
步骤s207：基于les耦合dpm的两相流流动。本技术实施例可以基于步骤s203中获取的稳定状态充分发展的湍流，及步骤s204、步骤s205、步骤s206建立的基于dpm(离散相)模型的固相颗粒运动计算，对固液两相流流动进行求解。
[0106]
本技术实施例可以在边界处释放颗粒，并在1个流动周期后停止颗粒释放，随后计算3个流动周期以获取颗粒充分扩散后的两相流流场，达到统计上的两相流稳定状态。在达到统计稳定状态之前，不收集任何不稳定的统计数据。达到统计稳定状态后，切换采样时间间隔，再计算2个流动周期并采集两相流非稳态数据。
[0107]
如图5所示，与利用相关技术中的球形阻力模型计算固液两相流的方法相比，本技术实施例可以修正阻力系数后计算得到的液相主流脉动速度与试验误差更小，可有效计算流体机械中固液两相流流动情况，且涉及了一种利用les获取湍流耗散率ε及kolmogorov长
度的方法，可为其他相关研究提供参考，同时。离散相模型允许对颗粒寻踪，因而可以获取颗粒在壁面处的撞击信息，为后续泥沙磨损研究奠定基础。
[0108]
根据本技术实施例提出的一种基于阻力系数修正的固液两相流数值计算方法，可以采用les及周期性边界条件获取充分发展的单相湍流流动，基于les获取的流动参数计算湍流耗散率及kolmogorov长度，建立含沙工况下修正阻力系数的两相流离散相模型，引入包含kolmogorov长度及颗粒粒径的函数，以考虑自由湍流对颗粒阻力的影响，计算两相流流动，求解固液两相流流动的计算结果，可以适用于流体机械中高雷诺数强湍流流体含沙工况，可准确模拟流体机械中固液两相的速度，数值计算结果准确度较高。由此，解决了相关技术中，基于wen-yu模型改进，在较低浓度固液两相流计算中对含沙阻力系数修正的适用范围有限，且对高湍流条件下的固液两相流流动计算的准确性较低的技术问题。