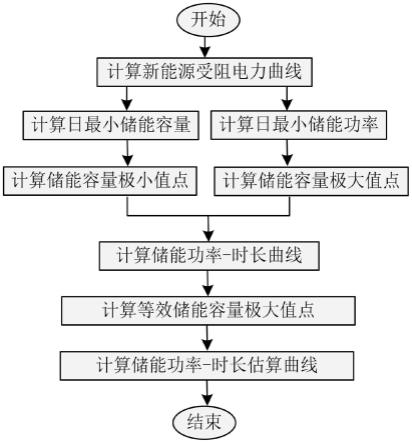
储能功率时长曲线估算方法与流程

1.本发明属于储能技术领域，涉及一种储能功率时长曲线估算方法。


背景技术：

2.加快构建以新能源为主体的新型电力系统，促进新能源占比逐渐提高，是实现碳达峰、碳中和的内在要求。随着新能源装机占比不断提高，火电等常规电源装机占比逐步减少，系统灵活性资源愈加紧缺。为实现系统发用电平衡，解决电力电量时空腾挪问题，通过配置储能提升系统灵活性，是新型电力系统发展的必然趋势。储能作为构建新型电力系统的重要技术和基础装备之一，通过合理配置储能规模，可显著提高系统电力调节能力和容量支撑能力。因此，开展储能在电力系统中功率时长的关系研究，从而为电力系统储能容量总体配置提供科学规划具有重要意义。
3.目前，含新能源系统的储能容量、储能功率和储能时长计算存在如下问题：在新能源利用率指标明确的情况下，通过时序或随机生产模拟法，多次计算得到满足给定新能源利用率目标的储能容量，是目前使用最为广泛的方法。一方面该方法需反复依赖生产模拟优化求解，计算方法费时重复，储能容量往往存在超配情况，且未能充分利用新能源弃电功率的统计学特性；另一方面，该方法无法得到储能功率时长的量化关系，为后续系统用电成本分析带来较多不便；更重要的是，相同的新能源利用率指标要求可通过不同的储能容量可实现，亟需通过储能功率时长曲线的关系，指导储能容量合理规划。


技术实现要素：

4.本发明的目的是提供一种储能功率时长曲线估算方法，该方法通过计算电力系统储能容量极小值点和储能容量极大值点，提出了储能功率时长曲线估算法，并可通过储能容量的合理取值，满足电力系统电力保供需求。
5.本发明所采用的技术方案是，储能功率时长曲线估算方法，具体包括如下步骤：
6.步骤1，根据规划水平年负荷、风电、光伏出力时间序列，常规机组最大、最小可调，计算新能源受阻出力；
7.步骤2，根据满足新能源利用率指标的日最小储能容量，计算储能容量极小值点；
8.步骤3，根据满足新能源利用率指标的日最小储能功率，计算储能容量极大值点；
9.步骤4，根据储能容量极大值点和极小值点求得储能功率时长曲线函数；
10.步骤5，根据系统新能源利用率指标误差要求，求得等效储能容量极大值点，得到储能功率时长近似曲线。
11.本发明的特点还在于：
12.步骤1的具体过程为：
13.步骤1.1，提出基于净负荷曲线的新型电力系统的弃电机理，具体为：
14.对有新能源接入的系统，运行中满足的发用电约束如下公式(1)所示：
15.p
gen
(t)+p
new
(t)＝p
l
(t)
ꢀꢀ
(1)；
16.其中，p
gen
(t)表示常规机组出力，p
l
(t)表示原负荷出力，p
gen
(t)表示新能源出力；
17.定义净负荷曲线为定义净负荷曲线为值为原负荷曲线减去新能源曲线p
new(t)
，如下公式(2)所示：
[0018][0019]
从新能源消纳角度来看，产生弃电的原因是常规机组最小出力大于净负荷曲线，如下公式(3)所示：
[0020][0021]
其中，p
gen,min
表示常规机组最小可调力。
[0022]
步骤1.2，计算新能源受阻出力，具体为：
[0023]
记新能源受阻出力为p
new,lose
(t)，某一刻新能源受阻电力如下公式(4)所示：
[0024][0025]
步骤2的具体过程为：
[0026]
步骤2.1，计算满足新能源利用率的日最小储能容量，具体为：
[0027]
设系统计算或采样步长为δt，记新能源日受阻电量为q
new,lose
(t)，则某一日新能源弃电量q
new,lose
如下公式(5)所示：
[0028][0029]
其中，t是一日的时长，通过公式(5)求得一年中每天的弃电量并进行升序排列，得到新能源年弃电量持续曲线记系统中储能配置容量为s，新能源全年理论发电量为q
new
，则新能源利用率η由公式(6)～(8)求得：
[0030][0031][0032][0033]
其中，p
new
为新能源每天的发电量，d是一年的天数，n是一年的时长，在给定新能源消纳目标的基础上，记满足新能源利用率需求的日最小储能容量为s
new,lose，min
，由公式(9)求得：
[0034][0035]
步骤2.2，求解系统的储能容量极小值点，具体为：
[0036]
定义储能容量极小值s
min
为计算步长δt和储能功率极大值点p
s,max
确定的点，这里将坐标点[δt,p
s,max
]称为储能容量极小值点，如公式(10)所示：
[0037]smin
＝δt
×
p
s,max
ꢀꢀ
(10)；
[0038]
在采样时间δt＝1时，式(9)求得的储能容量s
new,lose，min
就为储能容量极小值，储能功率极大值p
s,max
在数值上就是储能容量极小值：
[0039]smin
＝s
new,lose，min
ꢀꢀ
(11)；
[0040]
p
s,max
＝s
new,lose，min
ꢀꢀ
(12)。
[0041]
步骤3的具体过程为：
[0042]
步骤3.1，计算满足新能源消纳所需的最小储能功率，具体为：
[0043]
通过新能源受阻电力8760曲线，并将该曲线按升序排列，得到新能源年受阻电力持续曲线记储能功率为ps，满足新能源消纳所需的最小储能功率为p
s,new,min
，其满足公式(13)、(14)：
[0044][0045][0046]
步骤3.2，求解与最小储能功率对应的日最小储能时长，具体为：
[0047]
对于内部无网络约束的新能源系统，储能设施每天一充一放考虑，主要约束条件有：
[0048]
储能充放电功率约束如下：
[0049]
0≤p
ch
≤p
s,r
ꢀꢀ
(15)；
[0050]
0≤p
disch
≤p
s,r
ꢀꢀ
(16)；
[0051]
式中：p
ch
为系统中储能等效充电功率，p
disch
为等效放电功率，p
s,r
为等效额定功率；
[0052]
储能日充电电量约束如下：
[0053][0054]
式中：δ表示储能设备综合充放电效率；
[0055]
储能年充放电电量约束如下：
[0056][0057]
联立式(13)-(18)，即求得满足给定新能源利用率指标的最小储能时长t
s,new,min
：
[0058][0059]
步骤3.3，求解系统的储能容量极大值点，具体为：
[0060]
定义储能容量极大值s
max
为最小储能功率p
s,min
和储能时长极大值t
s,max
确定，如公式(20)所示，此时将坐标点[t
s,max
,p
s,min
]称为储能容量极大值点：
[0061]smax
＝t
s,max
×
p
s,min
ꢀꢀ
(20)；
[0062]
显然，最小储能功率p
s,min
和储能时长极大值点t
s,max
可表示为(21)、(22)：
[0063]
p
s,min
＝p
s,new,min
ꢀꢀ
(21)；
[0064]
t
s,max
＝t
s,new,min
ꢀꢀ
(22)。
[0065]
步骤4的具体过程为：
[0066]
由于满足一定新能源利用率指标的储能功率随着储能时长的增大而下降，因此，通过如下公式(23)多次计算得到各时长下的功率值：
[0067][0068]
步骤5的具体过程为：
[0069]
将提升后的最小储能功率对应的容量重新定义为等效储能极大值，表示为：
[0070]smax,eq
＝t
s,max,eq
×
p
s,min,eq
ꢀꢀ
(24)；
[0071]
式中：t
s,max,eq
表示等效最大储能时长，p
s,min,eq
等效最小储能功率，则式(23)可表示为：
[0072][0073]
储能容量极大值大于等效储能容量极小值，若两者的差值为：
[0074]
σ＝s
max-s
min
(26)；
[0075]
当差值σ较小时，储能功率时长函数关系可近似为：
[0076][0077]
设系统配置的储能容量用s
max,eq
近似后，每日增配的储能容量均可满充，新能源利用率较目标利用率最大偏大量记为κ，表示为
[0078][0079]
规划工作中，要求在[δt,t
s,max,eq
]区间配置的储能容量计算的新能源利用率和实际利用率偏差量κ不大于θ个百分点，则通过式(28)，可得满足式(27)成立的条件为
[0080][0081]
令公式(29)中的方程取等号，得等效最大储能时长t
s,max,eq
和等效最小储能功率p
s,min,eq
；
[0082]
由式(29)可知，随着系统中新能源发电量的提升，可允许的储能容量极大值和极
小值点的差值变大，即公式(27)的适用性越好。
[0083]
本发明的有益效果如下：
[0084]
1.本发明所提方法，通过储能容量极大值点和储能容量极小值点的计算，可快速获得储能功率时长曲线的近似曲线函数，第一次通过数学表达式的形式量化了上述关系，其原理直观明了、易于理解、适用性好，且便于计算。
[0085]
2.本发明所提方法，可以指导新能源场站级，及含有新能源的市级、省级、区域电网中储能容量的规划配置，对于提升新能源消纳水平、满足电力系统保供安全、促进储能产业健康持续发展意义重大。
[0086]
3.本发明所提方法，可以有效阐述各类储能技术在满足新能源利用率指标上的等效功效，不在刻意的要求储能技术要达到规定的储能时长，有助于各类储能技术发挥各自特效，为各类储能技术的合理规划提供了理论分析手段，为降低电力系统储能配置成本提供了量化分析方法。
附图说明
[0087]
图1是本发明储能功率时长曲线估算方法的流程图；
[0088]
图2是本发明储能功率时长曲线估算方法提出的以新能源为主体的新型电力系统中基于净负荷曲线的新能源弃电机理说明图；
[0089]
图3是本发明储能功率时长曲线估算方法提出的满足新能源利用率指标的日最小储能容量计算示意图；
[0090]
图4是本发明储能功率时长曲线估算方法提出的满足新能源利用率所需的最小储能功率计算示意图；
[0091]
图5是本发明储能功率时长曲线估算方法提出的通过储能容量极大值点和储能容量极小值点，计算储能功率时长估算曲线说明图；
[0092]
图6是本发明储能功率时长曲线估算方法提出的实际满足新能源利用指标的储能功率时长曲线和估算法提出的储能功率时长曲线的差异说明图；
[0093]
图7是本发明储能功率时长曲线估算方法提出的同时满足新能源利用率指标和系统保供需求的储能功率时长曲线。
具体实施方式
[0094]
下面结合附图和具体实施方式对本发明进行详细说明。
[0095]
本发明储能功率时长曲线估算方法，在满足新能源利用率指标要求的基础上，提出储能功率时长曲线估算法，其流程如图1所示，具体按照如下步骤实施：
[0096]
步骤1，根据新型电力系统的弃电机理，计算系统的弃电电力；根据规划水平年负荷、风电、光伏出力时间序列，常规机组最大、最小可调，分析基于净负荷曲线的弃电机理，计算新能源受阻出力，机理见图2所示。
[0097]
步骤1.1，提出基于净负荷曲线的新型电力系统的弃电机理：
[0098]
对有新能源接入的系统，运行中需满足的发用电约束为(1)式。式中，p
gen
(t)表示常规机组出力，p
l
(t)表示原负荷出力，p
gen
(t)表示新能源出力。
[0099]
p
gen
(t)+p
new
(t)＝p
l
(t)
ꢀꢀ
(1)；
[0100]
定义净负荷曲线为其值为原负荷曲线减去新能源曲线，见公式(2)所示。
[0101][0102]
从新能源消纳角度来看，产生弃电的原因是常规机组最小出力大于净负荷曲线，可表示为公式(3)。p
gen,min
表示常规机组最小可调。
[0103][0104]
步骤1.2，计算新能源受阻出力
[0105]
可选的，记新能源受阻出力为p
new,lose
(t)，某一刻新能源受阻电力可表示为公式(4)。
[0106][0107]
步骤2，根据满足新能源利用率指标的日最小储能容量，计算储能容量极小值点；通过新能源受阻电力曲线，刻画新能源日弃电量年持续曲线，然后计算满足新能源利用率的日最小储能容量，并计算储能容量极小值点，其机理见图3所示。
[0108]
步骤2.1，计算满足新能源利用率的日最小储能容量：
[0109]
设系统计算或采样步长为δt(本发明均按照1小时计算，可按需求进一步减小计算步长)。计算全年8760小时的新能源受阻出力得到新能源受阻电力8760曲线，记新能源日受阻电量为q
new,lose
(t)，则某一日新能源弃电量可表示为公式(5)。
[0110][0111]
(5)式中：t是一日的时长。通过公式(5)求得一年中每天的弃电量并进行升序排列，得到新能源年弃电量持续曲线记系统中储能配置容量为s，新能源全年理论发电量为q
new
，则新能源利用率η可由公式(6)求得。
[0112][0113][0114][0115]
(6)、(7)式中，d是一年的天数，n是一年的时长。在给定新能源消纳目标的基础上，记满足新能源利用率需求的日最小储能容量为s
new,lose，min
，其值可由公式(9)求得。
[0116][0117]
步骤2.2，求解系统的储能容量极小值点
[0118]
定义储能容量极小值s
min
为计算步长δt和储能功率极大值点p
s,max
确定的点，这里将坐标点[δt,p
s,max
]称为储能容量极小值点。如公式(10)所示。
[0119]smin
＝δt
×
p
s,max
ꢀꢀ
(10)；
[0120]
其具有的物理意义是：若储能容量为储能容量极小值，在[0,δt]时间间隔内，储
能功率在大于等于p
s,max
的情况下，新能源的利用率不随储能功率的增大而发生变化，即储能功率时长的乘积恒等于储能容量极小值，构成一个反比例函数。
[0121]
显然，在采样时间δt＝1时，式(9)求得的储能容量s
new,lose，min
就为储能容量极小值，储能功率极大值p
s,max
在数值上就是储能容量极小值。
[0122]smin
＝s
new,lose，min
ꢀꢀ
(11)；
[0123]
p
s,max
＝s
new,lose，min (12)；
[0124]
步骤3，根据满足新能源利用率指标的日最小储能功率，计算储能容量极大值点；通过新能源受阻电力曲线，刻画新能源受阻电力年持续曲线，计算满足新能源利用率的最小储能功率，并计算储能容量极大值点，其原理见图4所示：
[0125]
步骤3.1，计算满足新能源消纳所需的最小储能功率
[0126]
通过新能源受阻电力8760曲线，将其升序排列，得到新能源年受阻电力持续曲线记储能功率为ps，满足新能源消纳所需的最小储能功率为p
s,new,min
，其满足公式(13)、(14)。
[0127][0128][0129]
步骤3.2，求解与最小储能功率对应的日最小储能时长；
[0130]
对于内部无网络约束的新能源系统，储能设施每天一充一放考虑，主要约束条件有：
[0131]
储能充放电功率约束：
[0132]
0≤p
ch
≤p
s,r
ꢀꢀ
(15)；
[0133]
0≤p
disch
≤p
s,r
ꢀꢀ
(16)；
[0134]
式中：p
ch
为系统中储能等效充电功率，p
disch
为等效放电功率，p
s,r
为等效额定功率。
[0135]
储能日充电电量约束
[0136][0137]
式中：δ表示储能设备综合充放电效率。
[0138]
储能年充放电电量约束
[0139][0140]
联立式(13)-(18)，即可求得满足给定新能源利用率指标的最小储能时长t
s,new,min
。
[0141][0142]
步骤3.3，求解系统的储能容量极大值点：
[0143]
定义储能容量极大值s
max
为最小储能功率p
s,min
和储能时长极大值t
s,max
确定，如公式(20)所示。这里将坐标点[t
s,max
,p
s,min
]称为储能容量极大值点。
[0144]smax
＝t
s,max
×
p
s,min
ꢀꢀ
(20)；
[0145]
其具有的物理意义是：在最小储能功率确定的情况下，和其相对应的必有一个极大的储能时长t
s,max
，由p
s,min
和t
s,max
确定的储能容量满足新能源利用率指标要求，且在储能时长大于t
s,max
情况下，新能源利用率不在变化。
[0146]
显然，最小储能功率p
s,min
和储能时长极大值点t
s,max
可表示为(21)、(22)
[0147]
p
s,min
＝p
s,new,min
ꢀꢀ
(21)；
[0148]
t
s,max
＝t
s,new,min
ꢀꢀ
(22)；
[0149]
这里需要说明的，可以通过满足新能源利用率的最小储能功率计算对应的储能容量极大值点。实际中，因和新能源消纳对应的最小储能容量相对较小、储能时长偏大，故可按照保供需求对应的储能功率或者将储能时长极大值控制在6-8小时左右(目前电化学储能配置时长一般2-4小时左右、抽蓄6-8小时左右)反算储能容量极大值点。
[0150]
步骤4，根据储能容量极大值点和储能容量极小值点，提出储能功率时长曲线函数关系；在步骤2、3确定的满足新能源利用指标要求的储能容量极大值点和储能容量极小值点的基础上,得到储能功率时长曲线。其原理见图5所示。
[0151]
一般情况下，满足一定新能源利用率指标的储能功率随着储能时长的增大而下降(这里需要说明的是，一定的储能功率对应一个最小的储能时长，两者乘积确定的储能容量是满足给定新能源利用率的最小容量，因此这里所说的储能功率时长函数关系，实质是满足新能源利用率指标的下边界点，位于该储能功率时长曲线上方的点均是满足的点，本文的函数关系是指下边界)，两者的关系受多方面因素制约，只能多次计算得到各时长下的功率值，即如式(23)所示：
[0152][0153]
公式(23)中的三段分段函数中：
[0154]
第一段：储能时长位于[0，δt]之间时，储能功率时长构成一个反比例函数，两者的乘积等于储能容量极小值点。
[0155]
第二段：储能时长位于[δt,t
s,max
]之间时，可由公式(15)-(19)求解得到，通过不同储能功率求解得到对应的最小储能时长，形成一组下边界值，计算过程繁杂，耗时量大。
[0156]
第三段：储能时长位于[t
s,max
，+∞]之间时，储能功率不随储能时长变化，恒为最小储能功率，为一条直线。
[0157]
步骤5，根据系统新能源利用率指标误差要求，求得等效储能容量极大值点，得到储能功率时长近似曲线，并针对电力系统保供需求，进一步拓展曲线适用性。其原理见图6所示。
[0158]
通过最小储能功率确定的储能容量一般偏大，实际配置点储能容量往往较储能容量极大值点小很多。故有必要增大最小储能功率，减少储能容量配置，将提升后的最小储能功率对应的容量重新定义为等效储能极大值，表示为
[0159]smax,eq
＝t
s,max,eq
×
p
s,min,eq
ꢀꢀ
(24)；
[0160]
式中：t
s,max,eq
表示等效最大储能时长，p
s,min,eq
等效最小储能功率。
[0161]
则式(23)可表示为
[0162][0163]
一般情况下，储能容量极大值大于等效储能容量极小值，若两者的差值为
[0164]
σ＝s
max-s
min
(26)；
[0165]
当差值σ较小时，储能功率时长函数关系可近似为
[0166][0167]
显然，当储能时长位于[δt,t
s,max,eq
]之间时，利用式(27)计算的新能源利用率较实际利用率相对偏高。设系统配置的储能容量用s
max,eq
近似后，每日增配的储能容量均可满充，新能源利用率较目标利用率η最大偏大量记为κ，表示为
[0168][0169]
规划工作中，要求在[δt,t
s,max,eq
]区间配置的储能容量计算的新能源利用率和实际利用率偏差量κ不大于θ个百分点，则通过式(28)，可得满足式(27)成立的条件为
[0170][0171]
令(29)中可得等效最大储能时长t
s,max,eq
和等效最小储能功率p
s,min,eq
。
[0172]
由式(29)可知，随着系统中新能源发电量的提升，可允许的储能容量极大值和极小值点的差值变大，即公式(27)的适用性越好。
[0173]
这里需求强调的是：式(27)虽然为求满足新能源利用率指标得到的储能功率时长关系，但只要满足系统保供所需的最小储能容量为s
l,gap，min
和最小储能功率p
l,gap,min
包含在上述求得的储能功率时长曲线上方，式(24)就可拓展为同时满足新能源利用率指标和系统保供需求的储能功率时长曲线，这一点对于以新能源为主体的新型电力系统的储能容量配
置至关重要，其原理见图7所示。