综合评价排水模型率定效果的方法与流程

本发明涉及计算机辅助设计，特别涉及综合评价排水模型率定效果的方法。

背景技术：

1、随着数字化转型在城市排水领域的快速推广，排水模型作为排水系统数字化中核心的计算引擎，也获得了越来越多的关注。

2、而且，最新修订的行业强制标准室外排水设计标准(gb 50014-2021)中也明确：当汇水面积大于2平方公里时，应采用数学模型法确定雨水设计流量。

3、在现有技术中，排水模型构建完成之后，为了保证排水模型的准确性，需要对排水模型进行率定工作。

4、而排水模型的率定工作涉及到大量参数，主要包括：率定时间段的选择，率定时间段内的降雨量的统计，模型模拟数据与实测数据过程的匹配程度，模拟数据峰值，峰值出现时间与实测数据的匹配程度。

5、在影响率定效果的众多参数中，影响最大的参数是率定时间段的选择。一般来说，排水模型的模拟时间少则1-2天，长则1年，在如此长的模拟时间中，需要选出1-3个典型的时间段(一般一个时间段为2-6个小时)来进行模型的率定工作。

6、此外，选取不同率定时间段内的降雨强度也对排水模型的率定效果有较大影响，行业内一般要求模型的率定需要考虑不同降雨等级(如小雨、中雨、大雨)的工况的率定。

7、而目前对于排水模型的率定，多采用人工选取一段时间进行简单纳什系数的计算来评估模拟的流量/液位与对应实测流量/液位过程的匹配程度，这种方法存在以下缺陷：

8、1、由于是工程师根据个人工程经验选取的一个时间段来进行率定，不能保证可以准确提取出率定效果最佳的一段数据。

9、2、由于进行模型率定判断过程只是采取了纳什系数一个判断条件来进行模型模拟数值与实测数据的过程匹配，没有综合考虑最大峰值以及最大峰距的拟合程度对于排水模型率定效果的影响。

10、3、由于率定过程没有考虑降雨等级(如小雨、中雨、大雨)对应模型率定成果的影响，不能很好的区分不同降雨等级下模型率定效果的一致性。

11、因此，如何对长历时的排水模型模拟结果和历史实测数据中进行批量的处理，根据设置好的条件，选取出率定效果最好的若干个时间段，并且综合评价排水模型的率定效果成为本领域技术人员急需解决的技术问题。

技术实现思路

1、有鉴于现有技术的上述缺陷，本发明提供综合评价排水模型率定效果的方法，实现的目的是既提高了模型的率定效率，又让工程师对于整个排水模型的率定质量情况有一个全面的了解，还可以统一排水模型的率定质量的评估标准：既考虑了不同降雨等级下模型率定的一致性，又减少了人为因素对于排水模型率定效果的影响。

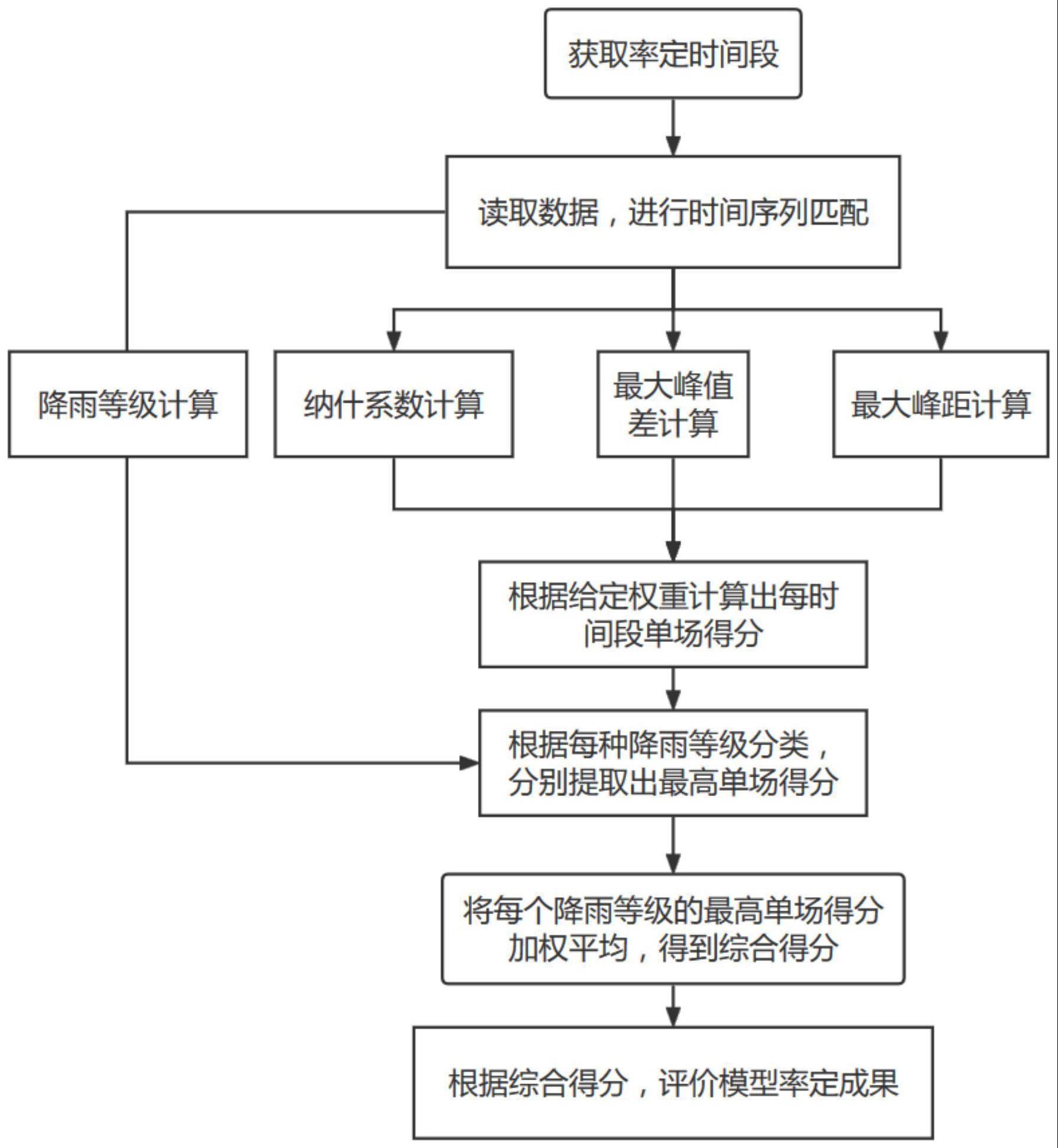
2、为实现上述目的，本发明公开了综合评价排水模型率定效果的方法，包括如下步骤：

3、步骤1、获取排水模型输出的模拟数据，以及相应的历史监测数据，进行时间序列匹配，获取率定时间段；

4、步骤2、率定参数计算，具体包括降雨等级计算、纳什系数计算、最大峰值差计算和最大峰距计算；

5、步骤3、多参数的加权的单场评分；

6、步骤4、综合得分计算；

7、步骤5、根据所述综合得分，评价率定效果。

8、优选的，所述排水模型为分段输出模拟数据，所述步骤1具体如下：

9、步骤1.1、利用sorted()函数，以关键字key为时间节点对读取的所有所述模拟数据进行升序排序；

10、步骤1.2、将每一段已经进完成排序的所述模拟数据的首尾时间节点与相应的所述历史监测数据进行对比，判断所述首尾时间节点是否与相应的历史监测数据一致；

11、若一致则两者时间是一一对应匹配的；

12、若不一致，则确定不一致的所述首尾时间节点在相应的所述历史监测数据中的索引位置；

13、然后通过所述索引位置将多余时间序列数据进行裁剪删除；

14、若不一致的所述首尾时间节点在在相应的所述历史监测数据中无法寻找到所述索引位置，则表示两者时间没有可匹配的时间段，返回检查数据。

15、优选的，所述步骤2采用窗口滑动计算的方式进行率定参数的计算；其中，合理的滑动的时间步长为5分钟-30分钟，和率定时间段为4小时-48小时。

16、更优选的，所述降雨等级计算具体如下：

17、首先，设置参数转，确保参与计算的数据步长保持一致；

18、然后，根据已完成所述时间序列匹配的所述模拟数据和所述历史监测数据，结合所述率定时间段计算出窗口滑动次数，以及每个率定时间段中最大降雨强度，再与相应规范匹配获得降雨等级。

19、更优选的，所述纳什系数计算的具体计算公式如下：

20、

21、其中，n为序列过程数据个数；ys为模拟值；yo为实测值；yo实测值的平均数；

22、首先，设置参数转，确保参与计算的数据步长保持一致；

23、然后，根据已完成所述时间序列匹配的所述模拟数据和所述历史监测数据，计算出窗口滑动次数；

24、设置循环次数等于滑动窗口的次数，窗口每滑动一次计算窗口内所有数据的所述纳什系数；

25、若所述纳什系数是一个含比值的指数，且出现分母为0的情况，则将nsec设置为一个-999的值表示为none。

26、更优选的，所述最大峰值差计算具体如下：

27、对于连续数据的波峰判断采用曲线斜率的方式；

28、若所述连续数据的数据节点处的斜率为0，则此处为波峰或者波谷。在实际数据中，很难直接计算获取曲线斜率为0的位置；

29、或者采用曲线变化形态的方式加以判断；

30、判断所述连续数据的数据节点前曲线处于上升状态,且所述数据节点后曲线处于下降状态，则该时间点上的数据为波峰数据；

31、在获取整个曲线的所有波峰位置以及波峰值后，利用波峰位置将所述模拟数据和所述历史监测数据一一对应，并计算波峰差的绝对值，并记录波峰差最大值作为所述最大峰值差。

32、更优选的，所述最大峰距的计算具体如下：

33、在述最大峰值差计算的基础上，在获取整个曲线的所有波峰位置以及波峰值后，同步记录波峰的时间位置信息，通过循环遍历所有对应的波峰，计算所述模拟数据和所述历史监测数据对应波峰的时间跨度绝对值，最后记录最大峰距。

34、更优选的，所述步骤3具体如下：

35、步骤3.1、对所述最大峰值差和所述最大峰距进行归一化处理到统一的量纲；所述统一的量纲为[0,1]；

36、步骤3.2采用最大最小值归一化的方法，分别寻找所述最大峰值差列表的最大峰值和最小峰值，然后根据最大最小值归一化公式，利用最大峰值减去当前峰值，然后除以最大峰值减去最小峰值获得所述最大峰值差的归一化结果；

37、所述最大峰距进行归一化处理的计算方式与最大峰值的计算方式一致；

38、采用如下公式对加权的单场评分进行计算：

39、scorei＝w1·nseci+w2·(1-vi)+w3·(1-di)；

40、其中，scorei为单场得分；w1为纳什系数权重；nseci为单场的纳什系数；w2为最大峰值差权重；vi为归一化后的最大峰值差；w3为最大峰距权重；d为归一化后的最大峰距差。

41、更优选的，所述步骤4具体如下：

42、根据步骤3中得出的单场得分，对不同的所述降雨等级进行综合评分，具体公式如下：

43、scorefinal＝k1·score小雨+k2·score中雨+k3·score大雨；

44、其中，scorefinal为排水模型率定综合得分；k1为小雨工况权重；score小雨为小雨工况下最佳的单场得分；k2为中雨工况权重；score中雨为中雨工况下最佳的单场得分；k3为大雨工况权重；score大雨为大雨工况下最佳的单场得分。

45、优选的，所述步骤5具体如下：

46、根据所述综合得分率定评价效果具体如下：

47、所述综合得分小于60，评价效果为较差；

48、所述综合得分大于等于60，且小于80，评价效果为良好；

49、所述综合得分大于等于80，且小于等于100，评价效果为优秀。

50、本发明的有益效果：

51、本发明可以在短时间内自动完成不同雨污水排水模型的率定成果分析，并且可以生成不同降雨等级下排水模型最优的纳什系数，单场得分，综合得分以及排水模型率定效果。

52、本发明可以对小雨、中雨、大雨工况下率定效果最好的时间段，纳什系数，单场得分，综合得分以及率定效果通过图像与图表的形式展现出来，方便工程师基于直观的数据进行排水模型率定效果的评估工作。

53、以下将结合附图对本发明的构思、具体结构及产生的技术效果作进一步说明，以充分地了解本发明的目的、特征和效果。