地下流动系统热-水动力-化学多场耦合数值模拟的方法

1.本技术涉及co2地质封存及其资源化利用技术领域，具体地涉及一种地下流动系统热-水动力-化学多场耦合数值模拟的方法。


背景技术：

2.二氧化碳气驱强化采油(co
2 enhanced oil recovery，co
2-eor)是碳捕获、利用与封存(carbon capture，utilization and storage，ccus)中的一项成熟技术。其增采的机理主要来源于溶解在油相中的co2降低了油相的粘度和表面张力，提高油相的渗透性，改善了二次采油形成的粘度指进，同时增大了注入流体在整个开采层的波及效率，进而延长了油田甚至成熟油田的使用寿命。co2在油相中的溶解度随着温压条件及原油性质存在差异，在一定条件下其和原油会发生混相或近混相，此时原油流动性将大大改善，同时获得较好的提高采收率效果。然而，该技术的另一个最大的特点则是注入的co2为酸性气体，且注入后会溶解在地层水中，降低地层ph值，打破系统中原有的水-岩平衡，进而引发一系列的地球化学反应。而溶解水相的co2存在形式hco
3-以及碳酸岩固相也因此形成，构成碳封存的较稳定的封存形式被安全封存在地下。评估co
2-eor技术的封存潜力似乎与其增采效率是相矛盾的，这也是该技术中碳循环及归宿以及碳封存潜力评价在以往的研究中没有得到足够重视的主要原因。
3.数值模拟是油田工程开发评价和预测的主要方法，遗憾的是前人多集中探讨该co
2-eor技术获得更高采收率的方案及方法，而缺乏对co2注入后发生的水-岩-气反应及地层孔渗特征变化的定量刻画。目前，成熟的油田模拟软件有加拿大发布的cmg(computer modeling group)和美国发布的eclipse。其中，cmg是一款集多相流、力学、地球化学和井筒为一体的综合油田开发模拟软件，模拟结果具有一定的行业标准的权威性。相比eclipse，cmg对水-岩反应的考虑能力使其成为研究co2-eor技术固碳效果的主要模拟软件。cmg中矿物的溶解和沉淀反应速率是根据过渡态理论(transition state theory)计算的，考虑了影响地球化学反应速率的中性机制。然而，已有研究表明，co2注入后，ph值显著降低，甚至低于5，多数矿物的溶解和沉淀反应速率受三种机制的影响，包括中性机制、酸性机制及碱性机制。考虑到矿物封存为最安全的碳封存形式，对于co2注入油层后地球化学反应还需要更准确的计算方法。


技术实现要素：

4.本技术实施例的目的是提供一种地下流动系统热-水动力-化学多场耦合数值模拟的方法，用以解决现有技术中对于co2油层后地球化学反应的计算准确度较低的问题。
5.为了实现上述目的，本技术第一方面提供一种地下流动系统热-水动力-化学多场耦合数值模拟的方法，包括：
6.获取初始流体及化学反应动力学参数；
7.根据初始流体及化学反应动力学参数建立多相多组分多场耦合的控制方程；
8.利用立方型状态方程确定各个相态的组成组分平衡方程；
9.利用多相态的变形达西定律，确定各相态的流动方程；
10.根据组成组分平衡方程和流动方程求解第一个时间步的控制方程的差分形式；
11.在控制方程的差分形式保持平衡的情况下，进行地球化学系统的求解，完成第一个时间步的计算；
12.在控制方程的差分形式没有保持平衡的情况下，继续下一个迭代步的运算，直至控制方程保持平衡后结束运算；
13.其中，控制方程的差分形式被定义为：
[0014][0015]
其中，为残差，mk表示组分k的质量或能量累积项，fk为组分k进入或流出量，qk为组分k的源汇项，e为迭代步，δt为迭代步e与e+1间的时间差，n、m分别为网格n与网格m，vn为网格n的面积，a
nm
与f
nm
为网格n、网格m之间的连接面积及流入(流出)量。
[0016]
在本技术实施例中，多相多组分多场耦合的控制方程满足下列公式：
[0017][0018]
其中，mk为组分k的质量或能量累积项，fk为组分k进入或流出量，qk为组分k的源汇项，n为网格n，vn为网格n的面积，γn为网格n的表面面积。
[0019]
在本技术实施例中，质量累积项mk满足下列公式：
[0020][0021]
其中，mk为质量累计项，ρ
β
、s
β
、分别为β相的密度、饱和度以及组分k在β相中的质量分数，φ为孔隙数，组分k包括烃组分cnhn，h2o及热，总组分为n+2，相态β包括气相、液相、油相和固相；
[0022]
能量累积项mk满足下列公式：
[0023][0024]
其中，mk为能量累积项，ρ
β
为β相的密度，s
β
为β相的饱和度，h
β
为β相流体的焓值，为动能，gz为重力势能，u
β
为流体流速，z为流体的相对高度，φ为孔隙数，ρr为岩体骨架密度，cr为岩体比热容，t为网格温度。
[0025]
在本技术实施例中，质量流量fk满足下列公式：
[0026][0027]
其中，f
κ
为k组分的质量流量，ρ
β
为β相的密度，s
β
为β相的饱和度，u
β
为流体流速；
[0028]
能量流量fk满足下列公式：
[0029]
[0030]
其中，f
κ
为k组分的能量流量，ρ
β
为β相的密度，s
β
为β相的饱和度，u
β
为流体流速，h
β
为流体焓值，为热传导项，λ为热传导系数，为动能，gz为重力势能，θ为流动方向与重力方向的夹角。
[0031]
在本技术实施例中，利用立方型状态方程确定各个相态的组成组分平衡方程包括：
[0032]
利用pr立方方程确定水组分在气相的平衡方程、水组分在油相的平衡方程和烃组分在气、油相的平衡方程。
[0033]
在本技术实施例中，水组分在气相的平衡方程满足下列公式：
[0034][0035]
其中，为水组分在气相中的平衡摩尔分数，p
sat
(t)为当前温度下水的饱和蒸气压，p为实际总压力；
[0036]
水组分在气相的平衡方程满足下列公式：
[0037][0038]
其中，为水组分在油相中的平衡摩尔分数，solu(t)为温度条件t下水组分在油相中的溶解度，po为参考压力；
[0039]
在本技术实施例中，烃组分在气、油相的平衡方程满足下列公式：
[0040]fi
(g)＝fi(o)，where fi＝pφixi，i＝1，
…
，nhc；
[0041]
其中，fi(g)为组分i在气相中的逸度，fi(o)为i在油相中的逸度，fi为逸度，p为压力，φi为组分i的逸度系数，xi为i组分的摩尔分数，i为组分。
[0042]
在本技术实施例中，利用多相态的变形达西定律，确定各相态的流动方程包括：
[0043]
通过stoneii模型或通过coats模型确定确定油相的相对渗透率函数。
[0044]
在本技术实施例中，通过stoneii模型确定的油相的相对渗透率函数满足下列公式：
[0045][0046]
其中，k
rocw
为原生水饱和度(s
wc
)下的油相相对渗透率，k
row
为sg＝0时的油相相对渗透率，k
rw
为与sw相关的水相相对渗透率函数，k
rog
为当sw＝s
wc
时，与sg相关的油相相对渗透率，k
rg
为与sg相关的气相相对渗透率函数；
[0047]
通过coats模型确定的油相的相对渗透率函数满足下列公式：
[0048]kro
＝k
roca
[(k
roa
+k
ra
)(k
rog
+k
rg
)-k
ra-k
rg
]；
[0049]
其中，k
ro
为油相相对渗透率，k
roca
为死端水饱和度时油相相对渗透率，k
roa
为油-水相对渗透率，k
ra
为水相相对渗透率，k
rog
为油-气相对渗透率。
[0050]
本技术第二方面提供一种地下流动系统热-水动力-化学多场耦合数值模拟的装置，包括：
[0051]
存储器，被配置成存储指令；以及
[0052]
处理器，被配置成从存储器调用指令以及在执行指令时能够实现上述的地下流动系统热-水动力-化学多场耦合数值模拟的方法。
[0053]
通过上述技术方案，提供了一种同时考虑多组分油相及co2注入油层后反应地球化学的热-水动力-化学多场耦合数值模拟方法，从质量守恒和能量守恒出发，结合达西定律的多相推广计算流动过程以及多烃组分的相平衡计算及含油相的多相流体流动计算，利用积分有限差分的方法(ifdm)对连续的空间和时间进行离散，利用稳定共轭梯度法构建大型的稀疏矩阵，使得模型能应用于三维大型网格系统进行运算，利用迭代方法进行求解。本技术可应用于co2注入油层后封存或co2增强石油开采技术中，定量刻画co2溶解于水形成hco
3-甚至构成碳酸盐固相过程，克服了现有模型的不足，考虑了影响地球化学反应速率的三种机制，提高了对co2注入油层后地层地球化学反应计算的准确度。
[0054]
本技术实施例的其它特征和优点将在随后的具体实施方式部分予以详细说明。
附图说明
[0055]
附图是用来提供对本技术实施例的进一步理解，并且构成说明书的一部分，与下面的具体实施方式一起用于解释本技术实施例，但并不构成对本技术实施例的限制。在附图中：
[0056]
图1示意性示出了根据本技术实施例的地下流动系统热-水动力-化学多场耦合数值模拟的方法的流程示意图；
[0057]
图2示意性示出了根据本技术实施例的同时考虑多组分油相及co2注入油层后反应地球化学的热-水动力-化学多场耦合模型原理图；
[0058]
图3示意性示出了根据本技术一具体实施例的地下流动系统热-水动力-化学多场耦合数值模拟的方法的流程示意图；
[0059]
图4示意性示出了根据本技术实施例的地下流动系统热-水动力-化学多场耦合数值模拟的装置的结构框图。
具体实施方式
[0060]
为使本技术实施例的目的、技术方案和优点更加清楚，下面将结合本技术实施例中的附图，对本技术实施例中的技术方案进行清楚、完整地描述，应当理解的是，此处所描述的具体实施方式仅用于说明和解释本技术实施例，并不用于限制本技术实施例。基于本技术中的实施例，本领域普通技术人员在没有做出创造性劳动的前提下所获得的所有其他实施例，都属于本技术保护的范围。
[0061]
需要说明，若本技术实施例中有涉及方向性指示(诸如上、下、左、右、前、后
……
)，则该方向性指示仅用于解释在某一特定姿态(如附图所示)下各部件之间的相对位置关系、运动情况等，如果该特定姿态发生改变时，则该方向性指示也相应地随之改变。
[0062]
另外，若本技术实施例中有涉及“第一”、“第二”等的描述，则该“第一”、“第二”等的描述仅用于描述目的，而不能理解为指示或暗示其相对重要性或者隐含指明所指示的技术特征的数量。由此，限定有“第一”、“第二”的特征可以明示或者隐含地包括至少一个该特征。另外，各个实施例之间的技术方案可以相互结合，但是必须是以本领域普通技术人员能够实现为基础，当技术方案的结合出现相互矛盾或无法实现时应当认为这种技术方案的结
合不存在，也不在本技术要求的保护范围之内。
[0063]
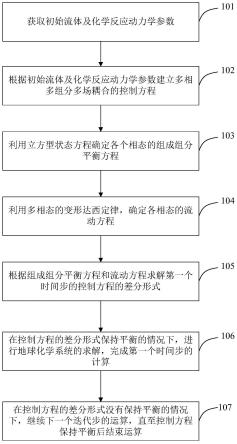
图1示意性示出了根据本技术实施例的地下流动系统热-水动力-化学多场耦合数值模拟的方法的流程示意图。如图1所示，在本技术实施例中，提供了一种地下流动系统热-水动力-化学多场耦合数值模拟的方法，该方法可以包括下列步骤：
[0064]
步骤101、获取初始流体及化学反应动力学参数；
[0065]
步骤102、根据初始流体及化学反应动力学参数建立多相多组分多场耦合的控制方程；
[0066]
步骤103、利用立方型状态方程确定各个相态的组成组分平衡方程；
[0067]
步骤104、利用多相态的变形达西定律，确定各相态的流动方程；
[0068]
步骤105、根据组成组分平衡方程和流动方程求解第一个时间步的控制方程的差分形式；
[0069]
步骤106、在控制方程的差分形式保持平衡的情况下，进行地球化学系统的求解，完成第一个时间步的计算；
[0070]
步骤107、在控制方程的差分形式没有保持平衡的情况下，继续下一个迭代步的运算，直至控制方程保持平衡后结束运算；
[0071]
其中，控制方程的差分形式被定义为：
[0072][0073]
其中，为残差，mk表示组分k的质量或能量累积项，fk为组分k进入或流出量，qk为组分k的源汇项，e为迭代步，δt为迭代步e与e+1间的时间差，n、m分别为网格n与网格m，vn为网格n的面积，a
nm
与f
nm
为网格n、网格m之间的连接面积及流入(流出)量。
[0074]
本技术实施例可应用于co2注入油层后封存或co2增强石油开采技术中，定量刻画co2溶解于水形成hco
3-甚至构成碳酸盐固相过程。本技术实施例从质量守恒和能量守恒出发，结合达西定律的多相推广计算流动过程，利用fortran语言编写多烃组分的相平衡计算及含油相的多相流体流动计算模块，利用积分有限差分的方法(ifdm)对连续的空间和时间进行离散，利用稳定共轭梯度法构建大型的稀疏矩阵，使得模型能应用于三维大型网格系统进行运算，利用newton-raphson迭代方法进行求解。利用fortran语言编写多烃组分的相平衡计算及含油相流体流动计算模块，耦合入现有的非等温多相反应溶质运移toughreact软件中进行反应地球化学过程的计算，实现co2注入油层后，孔隙介质内存在的多相、多组分热-水动力-化学多场耦合的数值模拟及分析。如图2所示，图2示意性示出了根据本技术实施例的同时考虑多组分油相及co2注入油层后反应地球化学的热-水动力-化学多场耦合模型原理图。
[0075]
在本技术实施例中，可以根据获取的初始流体及化学反应动力学参数建立多相多组分多场耦合的控制方程，其中，建立多组分多场耦合的控制方程主要是根据质量守恒和能量守恒建立。再利用立方型状态方程(如pr立方方程)确定各个相态的组成组分平衡方程以及利用多相态的变形达西定律，确定各相态的流动方程。进一步地，可以将fortran编写的控制方程、组成组分平衡方程以及各相态的流动方程耦合入toughreact软件中，进行第一个时间步的渗流、热及地球化学计算的求解。即根据组成组分平衡方程和流动方程求解第一个时间步的控制方程的差分形式：
[0076][0077]
在控制方程的差分形式保持平衡(即)的情况下，进行地球化学系统的求解，完成第一个时间步的计算。将当前时间步求得的地球化学求解结果体现的孔隙度及co2气体的逸度传递回上述步骤中，继续下一个迭代步的运算，直至控制方程保持平衡后结束运算。
[0078]
本技术实施例根据建立的多相多组分多场耦合的控制方程，对系统进行整体的稳定性控制；再利用pr立方方程求解油气中各烃组分的相平衡计算，理论基础严谨，通用性强；进而进行各相态的流动计算，通过以上步骤实现热-水动力场的耦合。再之后，将构建的含油相的渗流模块耦合入同用fortran编写的toughreact软件中，保证了渗流、热及地球化学计算的求解准确性，实现整体代码的稳定性及建模效率的保证。最后通过地球化学求解带来的孔隙度及co2气体逸度的变化传递到下一个时间步的计算中，实现了系统的整体热-水动力-化学多场耦合的数值模拟，克服了现有模型的不足，考虑了影响地球化学反应速率的三种机制，提高了对co2注入油层后地层地球化学反应计算的准确度。
[0079]
在本技术实施例中，多相多组分多场耦合的控制方程满足下列公式：
[0080][0081]
其中，mk为组分k的质量或能量累积项，fk为组分k进入或流出量，qk为组分k的源汇项，n为网格n，vn为网格n的面积，γn为网格n的表面面积。
[0082]
具体地，对于数值模拟，其最基本最核心的方程为质量守恒和能量守恒方程，其广义的方程如方程(1)所示。
[0083]
在本技术实施例中，对于任意质量组分k的计算，质量累积项mk满足下列公式：
[0084][0085]
其中，mk为质量累计项，ρ
β
、s
β
、分别为β相的密度、饱和度以及组分k在β相中的质量分数，φ为孔隙数，组分k包括烃组分cnhn，h2o及热，总组分为n+2，相态β包括气相、液相、油相和固相。
[0086]
对于能量累积项，与质量累积项不同。质量累积项只包括对流体的计算，而能量累积项除流体外，还包括对岩石骨架能量的计算，如公式(3)所示，能量累积项mk满足下列公式：
[0087][0088]
其中，mk为能量累积项，ρ
β
为β相的密度，s
β
为β相的饱和度，h
β
为β相流体的焓值，为动能，gz为重力势能，u
β
为流体流速，z为流体的相对高度，φ为孔隙数，ρr为岩体骨架密度，cr为岩体比热容，t为网格温度。
[0089]
上述在数值模拟里称之为局部热平衡，即认为网格内部流体与岩石的热交换是瞬时完成，网格内流体和岩石在任意时刻均具有相同温度。公式(3)考虑了流体的动能和重力
势能。由于能量的计算并没有一个基准，只看其绝对值并无意义，无论对于骨架，甚至是不同相态的流体，其参考体系均可任意选取，只要在同一模型中选取同一参考值即可。同理对于重力势能，也只要选取同一参考高度即可，此处重力势能主要针对于流体在井筒中的流动过程。
[0090]
在本技术实施例中，流体质量流动项无论在井筒或是储层中总体可表达为公式(4)，质量流量fk满足下列公式：
[0091][0092]
其中，f
κ
为k组分的质量流量，ρ
β
为β相的密度，s
β
为β相的饱和度，u
β
为流体流速；
[0093]
对于能量流动项，其表达式如公式(5)所示，能量流量fk满足下列公式：
[0094][0095]
其中，f
κ
为k组分的能量流量，ρ
β
为β相的密度，s
β
为β相的饱和度，u
β
为流体流速，h
β
为流体焓值，为热传导项，λ为热传导系数，为动能，gz为重力势能，θ为流动方向与重力方向的夹角。
[0096]
在本技术实施例中，利用立方型状态方程确定各个相态的组成组分平衡方程包括：
[0097]
利用pr立方方程确定水组分在气相的平衡方程、水组分在油相的平衡方程和烃组分在气、油相的平衡方程。
[0098]
对于油相系统，针对系统中含有多烃组分的特征，本次研究利用peng-robinson(pr)立方方程对多组分气、油相的热物性参数进行计算。该方程利用单组分方程结合二元相互作用系数计算多组分混合物，考虑了多组分之间的相互作用，使得预测结果更准确，方程有两种表达形式，如公式(6)所示：
[0099][0100]
其中，p为压力，r为气体常数，t为温度，v为体积，b为范德华斜体积，a为吸引力参数，z为压缩系数，a、b为二元交互作用系数。
[0101]
其它参数如分子量，临界性质，偏心因子以及理想气体的比热系数取自于已发表的属性数据库(poling等，2000)对于多组分的水相，在co
2-eor系统中，由于增加考虑了油相及油相中的多烃组分，考虑对水的热物性参数进行简化，co2相较于烃组分在水中有较大的溶解度，因此不考虑烃组分的溶解对水相热物性参数的影响，只考虑co2组分在水相中的溶解及其对水相密度的影响。因此，水相密度的计算表达式如公式(7)所示：
[0102][0103]
其中，ρ
aq
为水相密度，为co2组分在液相的摩尔分数，ρw为纯水的密度，为溶解co2的密度(kg/m3)，通过garcia(2001)所提出的公式进行计算，如公式(8)和公
式(9)所示。
[0104][0105]vφ
＝37.51-9.585
×
10-2
t+8.74
×
10-4
t
2-5.044
×
10-7
t3；
ꢀꢀ
(9)
[0106]
其中，为溶解co2的密度(kg/m3)，为co2的摩尔质量，v
φ
为co2的摩尔体积(cm3/l)，t为温度。
[0107]
在本技术实施例中，根据理想气体的假设条件，可通过该温度下水的饱和蒸汽压p
sat
(t)与实际压力p的比值计算水组分在气相中的平衡摩尔分数，水组分在气相的平衡方程满足下列公式：
[0108][0109]
其中，为水组分在气相中的平衡摩尔分数，p
sat
(t)为当前温度下水的饱和蒸气压，p为实际总压力；
[0110]
通过受温度控制的油相中的溶解度参数来计算水组分在油相中的平衡摩尔分数，水组分在气相的平衡方程满足下列公式：
[0111][0112]
其中，为水组分在油相中的平衡摩尔分数，solu(t)为温度条件t下水组分在油相中的溶解度，po为参考压力，通常为一个大气压。
[0113]
在本技术实施例中，将热力学关系式(6)应用于peng-robinson方程中，可计算逸度，其表达式如公式(8)所示，利用逸度平衡(公式14)计算烃组分在气-油相间的相平衡，逸度系数确定相分配系数(公式15)。
[0114]
烃组分在气、油相的平衡方程满足下列公式：
[0115][0116][0117]fi
(g)＝fi(o)，where fi＝pφixi，i＝1，
…
，nhc；
ꢀꢀ
(14)
[0118][0119]
其中，fi(g)为组分i在气相中的逸度，fi(o)为i在油相中的逸度，fi为逸度，p为压力，φi为组分i的逸度系数，xi为i组分的摩尔分数，i为组分；ki为相分配系数，φ
i，g
为组分i在气相中的逸度系数，φ
i，o
为组分i在油相中的逸度系数。
[0120]
在本技术实施例中，利用多相态的变形达西定律，确定各相态的流动方程包括：
[0121]
通过stoneii模型或通过coats模型确定油相的相对渗透率函数。
[0122]
具体地，对于传统水文地质学，其研究对象主要是多孔介质，用来描述多孔介质中水头和渗透流速的方程称之为达西定律。达西定律是经过大量实验，发现在一定条件下，渗
透流速与水力梯度成正比，如公式(16)所示。
[0123]
u＝k
·
i；
ꢀꢀ
(16)
[0124]
其中，u为渗透流速，i为水力梯度，即水头差与渗透路径之比，即其中k为比例系数，即为渗透系数，与多孔介质及流体性质相关，是多孔介质渗透率和流体的密度及动力粘度的函数，其表达式为：
[0125][0126]
其中，k为渗透系数，k为渗透率，ρ为流体密度，g为重力加速率，μ动力粘滞性系数。
[0127]
整理可得到，也就是将流速与水头的关系转化为了流速与压力的关系，以适应多相流模拟的需要。因为多相流中，水头的概念无法用于气相流动的计算。
[0128]
以上是对单相流动流速的推导，将其推广至多相流动，需引入相对渗透率概念。因为达西定律是假设流体在整个过水断面上皆有流动，而实际上，由于多相的存在，每一相态都无法占满过水断面，相态之间互相影响流动，使得实际流动过程中的有效渗透率低于实际渗透率，有效渗透率与实际渗透率的比值我们称之为相对渗透率。
[0129]
当储层只有两相流体存在时，主要应用van genuchten-mualem模型(mualem，1976；van genuchten，1980)进行相对渗透率的计算。而对于co
2-eor系统，孔隙内多数为气、水、油三相同时存在，常用的三相相对渗透率的计算模型有stone ii模型及考虑相界面张力的coats模型。
[0130]
在本技术实施例中，通过stoneii模型确定的油相的相对渗透率函数满足下列公式：
[0131][0132]
其中，k
rocw
为原生水饱和度(s
wc
)下的油相相对渗透率，k
row
为sg＝0时的油相相对渗透率，k
rw
为与sw相关的水相相对渗透率函数，k
rog
为当sw＝s
wc
时，与sg相关的油相相对渗透率，k
rg
为与sg相关的气相相对渗透率函数。
[0133]
具体地，储层存在气、水、油三相条件时，应用stone ii模型进行相对渗透率的计算，它假设油相的相对渗透率是水-油及油-气系统相对渗透率数据的函数，而水-油及油-气系统的相对渗透率数据通常通过实验进行获得。
[0134]
coats模型与stone ii模型不同的是，它考虑相对渗透率为油-气相界面张力的函数，如下式所示。
[0135]
通过coats模型确定的油相的相对渗透率函数满足下列公式：
[0136][0137]kro
＝k
roca
[(k
roa
+k
ra
)(k
rog
+k
rg
)-k
ra-k
rg
]；
ꢀꢀ
(20)
[0138]
[0139][0140]
其中，k
ro
为油相相对渗透率，k
roca
为死端水饱和度时油相相对渗透率，k
roa
为油-水相对渗透率，k
ra
为水相相对渗透率，k
rog
为油-气相对渗透率；f(σ)为气-油界面张力的函数，s
air
为残余水饱和度，s
gr
为残余气饱和度，k
roca
为死端水饱和度时油相相对渗透率。
[0141]
在本技术实施例中，可以将fortran编写的多烃组分的相平衡计算及含油相流体流动计算模块，耦合入现有的非等温多相反应溶质运移toughreact软件中进行第一个时间步的渗流、热及地球化学计算。
[0142]
首先，可以构建化学平衡求解数学模型。化学系统是由一组原子或元素组成的，将包含系统中所有元素的一组离子组分作为初始组分，其余的物质均可由这些初始组分来表示，称为次级组分，并且次要组分的数量必须等于系统中化学反应方程的数量，在代数方面，这些组分的表达可以被描述为一个线性无关数组。初始组分可以任意选择符合条件的离子组合，但一旦被确定，对于系统中次级组分的数组表达将是唯一的。一般表达式为：
[0143][0144]
其中，s为化学组分，j为初始组分指针数，i为次级组分指针数，nr为反应方程数(或次级组分个数)，v
ij
为次级组分i的反应方程中初始组分j的化学计量系数。
[0145]
根据组分质量守恒，组分j任意时刻的总浓度应该等于其零时刻的初始浓度，因此构建f
cj
＝t
j-t
j0
进行化学平衡状态判断，当f
cj
接近0时，说明与组分j有关的化学反应接近平衡，而当系统中所有组分f
cj
函数均接近0时，判定整个系统的化学反应接近平衡。其中tj和t
j0
的表达式如下：
[0146][0147][0148]fcj
＝t
j-t
j0
；
ꢀꢀ
(26)
[0149]
其中，f
cj
为j组分的浓度残差，t为基础组分的总浓度，上标0代表初始0时刻，c为浓度，下标的j，k，m，n，z，s分别代表基础组分、络合离子组分、平衡矿物、反应动力学平衡矿物、离子交换组分，及表面络合物组分，nc，nx，np，nq，nz，ns为相应组分的数量，v
kj
，v
mj
，v
nj
是基础组分j在相应复杂组分中的化学计量系数，rn为矿物溶解的动力学速率(沉淀为负，使用的单位是单位时间摩尔每千克水)，δtr为反应时间步的长度。
[0150]
接着，进行离子络合反应，假定反应处于局部平衡，根据质量作用定律求解次级组分i，次级组分i的浓度可表示为初始组分j浓度的函数：
[0151][0152]
其中，ci为次级组分i的摩尔浓度，cj为初级组分j的摩尔浓度，γi和γj为热力学活度系数，ki为平衡常数，v
ij
为次级组分i的反应方程中初始组分j的化学计量系数，nc为基础组分的数量。
[0153]
进一步，进行矿物溶解与沉淀，通过判断反应平衡常数与矿物饱和指数sim的大小确定矿物反应的方向(溶解或沉淀)，矿物的饱和指数表达式如下，若反应为平衡状态时，sim＝0。
[0154][0155]
其中，ωm为矿物饱和指数，km为平衡常数，m为矿物平衡反应指针数，cj为初级组分j的摩尔浓度，γj为热力学活度系数，v
mj
，nc为，n
p
同上。
[0156]
而对于矿物反应动力学溶解/沉淀条件的判定，则采用lasaga et al.(1994)提出的反应速率计算模型，表达式如下：
[0157][0158]
其中，rn为反应速率，负值表示沉淀，正值表示溶解，kn为与温度有关的速率常数(单位矿物表面积和单位时间下)，an为反应比表面积，矿物动力学饱和比。系数θ和η由实验确定，通常取1，为反应动力学平衡矿物的饱和指数，为nc个基础组分的浓度。反应速率常数kn采用arrhenius(lasaga，1984；steefel and lasaga，1994)公式计算：
[0159][0160]
其中，k为反应速率，ea为活化能，k
25
为25℃时的速率常数，r为气体常数，t为绝对温度。
[0161]
不同的ph值条件对反应速率常数k有不同的影响机制，采用以下数学表达式(lasaga et al.，1994；palandri and kharaka，2004)刻画不同ph值条件下的影响机制：
[0162][0163]
其中，nu，h和oh分别代表中性、酸性和碱性机制，a为组分的活度，n是幂指数(常数)，θ和η的值在不同的ph值影响机制中的计算是一致的。
[0164]
进一步的，进行阳离子交换反应，溶液中的游离阳离子与地层表面阳离子可发生阳离子交换反应。这个过程可以描述为可交换的阳离子和交换位点之间的平衡反应。平衡常数通常称为阳离子交换系数，它的值取决于溶液的离子强度。阳离子交换反应的一般表达式(appelo and postma，1993)为：
[0165][0166]
其中，vi和vj分别为游离阳离子和地层表面阳离子的化学计量系数(等于它们的电荷)，si和sj分别表示游离阳离子和地层表面阳离子，和表示与地层表面阳离子的交换位。
[0167]
反应的平衡常数计算公式为：
[0168]
[0169]
其中，为离子交换反应的平衡常数，aj为组分j的活度和是地层表面阳离子i的活度。
[0170]
根据vanselow理论，可以认为等于地层表面阳离子i的摩尔分数，计算公式为：
[0171][0172]
其中，cec为地层表面阳离子交换能力，zi与vi的物理意义一致。
[0173]
将以上化学平衡计算过程与公式(2)和(3)结合并带如公式(35)，利用积分有限差分法进行求解。控制方程的差分形式满足下列公式：
[0174][0175]
其中，为残差，mk表示组分k的质量或能量累积项，fk为组分k进入或流出量，qk为组分k的源汇项，e为迭代步，δt为迭代步e与e+1间的时间差，n、m分别为网格n与网格m，vn为网格n的面积，a
nm
与f
nm
为网格n、网格m之间的连接面积及流入(流出)量。r＝0代表方程收敛，当前时间步计算完成。将当前时间步求得的地球化学求解结果体现的孔隙度及co2气体逸度的变化传递回上述公式(15)中，进行下一个时间步的流动、热及地球化学计算的求解。
[0176]
介质孔隙度的变化与矿物的解/沉淀作用直接相关。程序中考虑了孔隙度受矿物的解/沉淀作用的影响，计算公式如下：
[0177][0178]
其中，φ为孔隙度，nm为矿物的数量，frm为矿物m在整个介质中的体积分数(包括孔隙)，fru为非反应岩相的体积分数，孔隙度的值随着frm的变化而变化且恒大于0。
[0179]
co2逸度的计算根据公式如下，其中k为反应平衡常数，ai为i组分在水相中的活度，fi，和yi分别为i组分的逸度、逸度系数和在气相中的摩尔分数，p
tot
为系统总压力。
[0180][0181][0182][0183]fi
＝φiyip
tot
。
ꢀꢀ
(39)
[0184]
将以上计算的孔隙度的co2逸度更新至公式(2)和(3)及(12)中，进行下一个时间步的计算。
[0185]
图3示意性示出了根据本技术一具体实施例的地下流动系统热-水动力-化学多场耦合数值模拟的方法的流程示意图。如图3所示，在一具体实施例中，包括如下步骤：
[0186]
初始化参数，包括水、co2和多烃组分；
[0187]
读取初始化学反应动力学参数，并为每个网格分配化学状态变量；
[0188]
迭代步kcyc＝kcyc+1，时间步长为δt。
[0189]
在一个时间步中，包括如下5个运算步骤：
[0190]
步骤1：求解流动和热流动方程；
[0191]
步骤2：求解组分相态平衡方程；
[0192]
步骤3：得到流动速率；
[0193]
步骤4：基于温度分布，求解溶解于水相组分间的溶质运移及气体组分的溶质运移；基于所有溶解组分的浓度和温度分布，调用化学计算模块进行单网格计算；判断是否收敛，若收敛，则更新化学状态变量至下个时间步，进入步骤5；否则，从固相、气相至溶解水相的质量传输，重新开始步骤4；
[0194]
步骤5：更新物性参数，继续迭代，直到方程平衡，迭代完毕，运算停止。
[0195]
图4示意性示出了根据本技术实施例的地下流动系统热-水动力-化学多场耦合数值模拟的装置的结构框图。如图4所示，本技术实施例提供一种地下流动系统热-水动力-化学多场耦合数值模拟的装置，可以包括：
[0196]
存储器410，被配置成存储指令；以及
[0197]
处理器420，被配置成从存储器410调用指令以及在执行指令时能够实现上述的地下流动系统热-水动力-化学多场耦合数值模拟的方法。
[0198]
具体地，在本技术实施例中，处理器420可以被配置成：
[0199]
获取初始流体及化学反应动力学参数；
[0200]
根据初始流体及化学反应动力学参数建立多相多组分多场耦合的控制方程；
[0201]
利用立方型状态方程确定各个相态的组成组分平衡方程；
[0202]
利用多相态的变形达西定律，确定各相态的流动方程；
[0203]
根据组成组分平衡方程和流动方程求解第一个时间步的控制方程的差分形式；
[0204]
在控制方程的差分形式保持平衡的情况下，进行地球化学系统的求解，完成第一个时间步的计算；
[0205]
在控制方程的差分形式没有保持平衡的情况下，继续下一个迭代步的运算，直至控制方程保持平衡后结束运算；
[0206]
其中，控制方程的差分形式被定义为：
[0207][0208]
其中，为残差，mk表示组分k的质量或能量累积项，fk为组分k进入或流出量，qk为组分k的源汇项，e为迭代步，δt为迭代步e与e+1间的时间差，n、m分别为网格n与网格m，vn为网格n的面积，a
nm
与f
nm
为网格n、网格m之间的连接面积及流入(流出)量。
[0209]
在本技术实施例中，多相多组分多场耦合的控制方程满足下列公式：
[0210][0211]
其中，mk为组分k的质量或能量累积项，fk为组分k进入或流出量，qk为组分k的源汇项，n为网格n，vn为网格n的面积，γn为网格n的表面面积。
[0212]
在本技术实施例中，质量累积项mk满足下列公式：
[0213]
[0214]
其中，mk为质量累计项，ρ
β
、s
β
、分别为β相的密度、饱和度以及组分k在β相中的质量分数，φ为孔隙数，组分k包括烃组分cnhn，h2o及热，总组分为n+2，相态β包括气相、液相、油相和固相；
[0215]
能量累积项mk满足下列公式：
[0216][0217]
其中，mk为能量累积项，ρ
β
为β相的密度，s
β
为β相的饱和度，h
β
为β相流体的焓值，为动能，gz为重力势能，u
β
为流体流速，z为流体的相对高度，φ为孔隙数，ρr为岩体骨架密度，cr为岩体比热容，t为网格温度。
[0218]
在本技术实施例中，质量流量fk满足下列公式：
[0219][0220]
其中，f
κ
为k组分的质量流量，ρ
β
为β相的密度，s
β
为β相的饱和度，u
β
为流体流速；
[0221]
能量流量fk满足下列公式：
[0222][0223]
其中，f
κ
为k组分的能量流量，ρ
β
为β相的密度，s
β
为β相的饱和度，u
β
为流体流速，h
β
为流体焓值，为热传导项，λ为热传导系数，为动能，gz为重力势能，θ为流动方向与重力方向的夹角。
[0224]
进一步地，处理器420可以被配置成：
[0225]
利用立方型状态方程确定各个相态的组成组分平衡方程包括：
[0226]
利用pr立方方程确定水组分在气相的平衡方程、水组分在油相的平衡方程和烃组分在气、油相的平衡方程。
[0227]
在本技术实施例中，水组分在气相的平衡方程满足下列公式：
[0228][0229]
其中，为水组分在气相中的平衡摩尔分数，p
sat
(t)为当前温度下水的饱和蒸气压，p为实际总压力；
[0230]
水组分在气相的平衡方程满足下列公式：
[0231][0232]
其中，为水组分在油相中的平衡摩尔分数，solu(t)为温度条件t下水组分在油相中的溶解度，po为参考压力；
[0233]
在本技术实施例中，烃组分在气、油相的平衡方程满足下列公式：
[0234]fi
(g)＝fi(o)，where fi＝pφpixi，i＝1，
…
，nhc；
[0235]
其中，fi(g)为组分i在气相中的逸度，fi(o)为i在油相中的逸度，fi为逸度，p为压力，φi为组分i的逸度系数，xi为i组分的摩尔分数，i为组分。
[0236]
进一步地，处理器420可以被配置成：
[0237]
利用多相态的变形达西定律，确定各相态的流动方程包括：
[0238]
通过stoneii模型或通过coats模型确定确定油相的相对渗透率函数。
[0239]
在本技术实施例中，通过stoneii模型确定的油相的相对渗透率函数满足下列公式：
[0240][0241]
其中，k
rocw
为原生水饱和度(s
wc
)下的油相相对渗透率，k
row
为sg＝0时的油相相对渗透率，k
rw
为与sw相关的水相相对渗透率函数，k
rog
为当sw＝s
wc
时，与sg相关的油相相对渗透率，k
rg
为与sg相关的气相相对渗透率函数；
[0242]
通过coats模型确定的油相的相对渗透率函数满足下列公式：
[0243]kro
＝k
roca
[(k
roa
+k
ra
)(k
rog
+k
rg
)-k
ra-k
rg
]；
[0244]
其中，k
ro
为油相相对渗透率，k
roca
为死端水饱和度时油相相对渗透率，k
roa
为油-水相对渗透率，k
ra
为水相相对渗透率，k
rog
为油-气相对渗透率。
[0245]
通过上述技术方案，提供了一种同时考虑多组分油相及co2注入油层后反应地球化学的热-水动力-化学多场耦合数值模拟方法，从质量守恒和能量守恒出发，结合达西定律的多相推广计算流动过程以及多烃组分的相平衡计算及含油相的多相流体流动计算，利用积分有限差分的方法(ifdm)对连续的空间和时间进行离散，利用稳定共轭梯度法构建大型的稀疏矩阵，使得模型能应用于三维大型网格系统进行运算，利用迭代方法进行求解。本技术可应用于co2注入油层后封存或co2增强石油开采技术中，定量刻画co2溶解于水形成hco
3-甚至构成碳酸盐固相过程，克服了现有模型的不足，考虑了影响地球化学反应速率的三种机制，提高了对co2注入油层后地层地球化学反应计算的准确度。
[0246]
本技术实施例还提供一种机器可读存储介质，该机器可读存储介质上存储有指令，该指令用于使得机器执行上述的地下流动系统热-水动力-化学多场耦合数值模拟的方法的流程示意图。
[0247]
本领域内的技术人员应明白，本技术的实施例可提供为方法、系统、或计算机程序产品。因此，本技术可采用完全硬件实施例、完全软件实施例、或结合软件和硬件方面的实施例的形式。而且，本技术可采用在一个或多个其中包含有计算机可用程序代码的计算机可用存储介质(包括但不限于磁盘存储器、cd-rom、光学存储器等)上实施的计算机程序产品的形式。
[0248]
本技术是参照根据本技术实施例的方法、设备(系统)、和计算机程序产品的流程图和/或方框图来描述的。应理解可由计算机程序指令实现流程图和/或方框图中的每一流程和/或方框、以及流程图和/或方框图中的流程和/或方框的结合。可提供这些计算机程序指令到通用计算机、专用计算机、嵌入式处理机或其他可编程数据处理设备的处理器以产生一个机器，使得通过计算机或其他可编程数据处理设备的处理器执行的指令产生用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的装置。
[0249]
这些计算机程序指令也可存储在能引导计算机或其他可编程数据处理设备以特
定方式工作的计算机可读存储器中，使得存储在该计算机可读存储器中的指令产生包括指令装置的制造品，该指令装置实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能。
[0250]
这些计算机程序指令也可装载到计算机或其他可编程数据处理设备上，使得在计算机或其他可编程设备上执行一系列操作步骤以产生计算机实现的处理，从而在计算机或其他可编程设备上执行的指令提供用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的步骤。
[0251]
在一个典型的配置中，计算设备包括一个或多个处理器(cpu)、输入/输出接口、网络接口和内存。
[0252]
存储器可能包括计算机可读介质中的非永久性存储器，随机存取存储器(ram)和/或非易失性内存等形式，如只读存储器(rom)或闪存(flash ram)。存储器是计算机可读介质的示例。
[0253]
计算机可读介质包括永久性和非永久性、可移动和非可移动媒体，可以由任何方法或技术来实现信息存储。信息可以是计算机可读指令、数据结构、程序的模块或其他数据。计算机的存储介质的例子包括，但不限于相变内存(pram)、静态随机存取存储器(sram)、动态随机存取存储器(dram)、其他类型的随机存取存储器(ram)、只读存储器(rom)、电可擦除可编程只读存储器(eeprom)、快闪记忆体或其他内存技术、只读光盘只读存储器(cd-rom)、数字多功能光盘(dvd)或其他光学存储、磁盒式磁带，磁带磁盘存储或其他磁性存储设备或任何其他非传输介质，可用于存储可以被计算设备访问的信息。按照本文中的界定，计算机可读介质不包括暂存电脑可读媒体(transitory media)，如调制的数据信号和载波。
[0254]
还需要说明的是，术语“包括”、“包含”或者其任何其他变体意在涵盖非排他性的包含，从而使得包括一系列要素的过程、方法、商品或者设备不仅包括那些要素，而且还包括没有明确列出的其他要素，或者是还包括为这种过程、方法、商品或者设备所固有的要素。在没有更多限制的情况下，由语句“包括一个
……”
限定的要素，并不排除在包括要素的过程、方法、商品或者设备中还存在另外的相同要素。
[0255]
以上仅为本技术的实施例而已，并不用于限制本技术。对于本领域技术人员来说，本技术可以有各种更改和变化。凡在本技术的精神和原理之内所作的任何修改、等同替换、改进等，均应包含在本技术的权利要求范围之内。