一种工程结构振动响应的复合显式时域分析方法

1.本发明涉及结构动力学技术领域，特别是涉及一种工程结构振动响应的复合显式时域分析方法及系统。


背景技术：

2.随着计算机技术的飞速发展，直接时间积分方法已广泛应用于求解工程结构的动态响应。大量有限元商业软件都将直接时间积分方法作为求解结构动态响应的核心算法。因此，提升时间积分方法的性能对求解工程结构的动态响应至关重要。
3.大致上，时间积分法可以分为显式时间积分法和隐式时间积分法。这两种方法各有优点和缺点，适用的求解对象不同。相比隐式方法，显式方法通常是条件稳定的，即需要更短的时间步长以保证计算结果收敛。然而，显式方法无需进行方程组的迭代求解，因此显式方法的单步计算效率高于隐式。显式方法在求解大型结构或非线性程度较高的问题时更具优势。
4.在现有的显式方法中，中心差分法(central difference method，cd法)是最为经典的单步方法，其已应用到ansys、abaqus和adina等著名有限元商业软件中。然而，cd法存在许多缺点，如数值耗散特性较差，稳定区间较短，精度阶数低等。数值耗散是对算法的计算精度影响最大的特性之一。优良的数值耗散特性需要在减少有限元离散化所引起的虚假的高频模态的同时尽可能地保留重要的低频模态。事实上，这对显式方法是不容易做到的。为了提升数值耗散特性，noh和bathe开发了一种复合时间积分方法(称为noh-bathe法，noh g,bathe k-j.an explicit time integration scheme for the analysis ofwave propagations.computers&structures 2013)，这种方法采用了两个子步的策略，可以达到较好的数值耗散特性，以及较大的稳定区间。该方法属于adina软件瞬态动力学响应分析的核心求解算法。但是，noh-bathe法在求解一些非线性问题(例如振动响应)上稳定性差，易获得不收敛的计算结果，且计算精度较低。
5.总的来说，现有的显式时间积分方法在非线性问题中的计算精度和稳定性的表现有待提高。


技术实现要素：

6.本发明的目的是提供一种工程结构振动响应的复合显式时域分析方法及系统，以提升工程结构振动响应的动力学分析的精度与稳定性。
7.为实现上述目的，本发明提供了如下方案：
8.本发明提供一种工程结构振动响应的复合显式时域分析方法，所述方法包括如下步骤：
9.采用空间单元离散法获取待求解工程结构的动力学控制模型和结构矩阵；所述结构矩阵包括：整体质量矩阵、整体阻尼矩阵和整体刚度矩阵；
10.基于所述动力学控制模型和结构矩阵，采用复合显式时间积分法对所述待求解工
程结构进行三分步迭代求解，确定振动载荷下所述待求解工程结构在每个整体步的动态响应物理量；所述动态响应物理量包括广义位移矢量、广义速度矢量和广义加速度矢量。
11.可选的，所述基于所述动力学控制模型和结构矩阵，采用复合显式时间积分法对所述待求解工程结构进行三分步迭代求解，确定振动载荷下所述待求解工程结构在每个整体步的动态响应物理量，具体包括：
12.利用如下公式确定振动载荷下所述待求解工程结构在第i+1个整体步的第一分步的动态响应物理量：
[0013][0014][0015][0016][0017]
其中，u(t
i+p
)、和分别表示在第i+1个整体步的第一分步的广义位移矢量、广义速度矢量和广义加速度矢量，u(ti)、和分别表示第i个整体步的广义位移矢量、广义速度矢量和广义加速度矢量，p表示单个的分步占整体步的比例，0《p《1，δt表示整体步的步长，表示第i+1个整体步的第一分步的中间过渡向量，m表示整体质量矩阵，k表示整体刚度矩阵，c表示整体阻尼矩阵，f(t
i+p
)表示第i+1个整体步的第一分步的振动载荷；
[0018]
根据待求解工程结构在第i+1个整体步的第一分步的动态响应物理量，利用如下公式确定振动载荷下所述待求解工程结构在第i+1个整体步的第二分步的动态响应物理量：
[0019][0020][0021][0022][0023]
其中，u(t
i+2p
)、和分别表示在第i+1个整体步的第二分步的广义位移矢量、广义速度矢量和广义加速度矢量，表示复合显式时间积分法中的未知系数向量，，f(t
i+2p
)表示第i+1个整体步的第二分步的振动载荷；
[0024]
根据待求解工程结构在第i+1个整体步的第一分步和第二分步的动态响应物理
量，利用如下公式确定振动载荷下所述待求解工程结构在第i+1个整体步的第三分步的动态响应物理量，作为振动载荷下所述待求解工程结构在第i+1个整体步的动态响应物理量：
[0025][0026][0027][0028][0029]
其中，表示第i+1个整体步的中间过渡向量，u(t
i+1
)、)、分别表示第i+1个整体步的广义位移矢量、广义速度矢量和广义加速度矢量，α表示的计算式中的计算比例系数，β表示u(t
i+1
)的计算式中的比例系数，γ和δ分别表示的计算式中的计算比例系数和的计算比例系数，f
i+1
表示第i+1个整体步的第三分步的振动载荷。
[0030]
可选的，所述基于所述动力学控制模型和结构矩阵，采用复合显式时间积分法对所述待求解工程结构进行分步长迭代求解，确定振动载荷下所述待求解工程结构在每个整体步的动态响应物理量，之前还包括：
[0031]
将初始时刻的广义位移向量和广义速度矢量作为初始广义位移矢量和初始广义速度矢量；
[0032]
根据所述初始广义位移矢量和初始广义速度矢量，利用所述动力学控制模型，求解振动载荷下所述待求解工程结构的初始广义加速度矢量。
[0033]
可选的，所述基于所述动力学控制模型和结构矩阵，采用复合显式时间积分法对所述待求解工程结构进行三分步迭代求解，确定振动载荷下所述待求解工程结构在每个整体步的动态响应物理量，之前还包括：
[0034]
确定待求解工程结构的自由参数为：
[0035][0036]
可选的，所述基于所述动力学控制模型和结构矩阵，采用复合显式时间积分法对所述待求解工程结构进行三分步迭代求解，确定振动载荷下所述待求解工程结构在每个整体步的动态响应物理量，之前还包括：
[0037]
求解方程|k-λm|＝0，获得多个特征根；
[0038]
根据多个所述特征根中的最大特征值确定整体步的步长的取值范围为
[0039][0040]
其中，k表示整体刚度矩阵，m表示整体质量矩阵，λ表示特征根，λ
max
表示最大特征值，δt表示整体步的步长，l表示稳定区间参数。
[0041]
可选的，l＝5.508。
[0042]
一种工程结构振动响应的复合显式时域分析系统，所述系统应用于上述的方法，所述系统包括：
[0043]
动力学控制模型和结构矩阵获取模块，用于采用空间单元离散法获取待求解工程结构的动力学控制模型和结构矩阵；所述结构矩阵包括：整体质量矩阵、整体阻尼矩阵和整体刚度矩阵；
[0044]
动态响应物理量迭代求解模块，用于基于所述动力学控制模型和结构矩阵，采用复合显式时间积分法对所述待求解工程结构进行三分步迭代求解，确定振动载荷下所述待求解工程结构在每个整体步的动态响应物理量；所述动态响应物理量包括广义位移矢量、广义速度矢量和广义加速度矢量。
[0045]
一种电子设备，包括存储器、处理器以及存储在所述存储器上并可在所述处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现上述的方法。
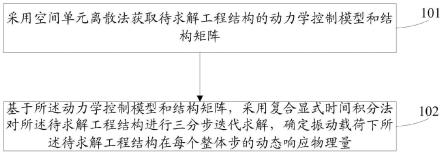
[0046]
一种计算机可读存储介质，所述存储介质上存储有计算机程序，所述计算机程序被执行时实现上述的方法。
[0047]
根据本发明提供的具体实施例，本发明公开了以下技术效果：
[0048]
本发明公开了一种工程结构振动响应的复合显式时域分析方法，所述方法包括如下步骤：采用空间单元离散法获取待求解工程结构的动力学控制模型和结构矩阵；基于所述动力学控制模型和结构矩阵，采用复合显式时间积分法对所述待求解工程结构进行三分步迭代求解，确定振动载荷下所述待求解工程结构在每个整体步的动态响应物理量；本发明采用复合显式时间积分法，并分三步进行迭代求解，克服了现有的显示时间积分法计算非线性问题时的技术缺陷，相比于现有的显式时间积分方法的计算精度和稳定性上都有较大提升。
附图说明
[0049]
为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动性的前提下，还可以根据这些附图获得其他的附图。
[0050]
图1为本发明提供的一种工程结构振动响应的复合显式时域分析方法的流程图；
[0051]
图2为本发明提供的一种工程结构振动响应的复合显式时域分析方法的原理图；
[0052]
图3为本发明实施例提供的算例1中的非线性工程结构的结构图原理图；
[0053]
图4为本发明实施例提供的算例1中的非线性工程结构的不同算法在0-5s内的计算结果对比图；
[0054]
图5为本发明实施例提供的算例1中的非线性工程结构的不同算法在200-205s内的计算结果对比图；
[0055]
图6为本发明实施例提供的算例2中的十层剪切框架结构的结构原理图；
[0056]
图7为本发明实施例提供的算例2中的十层剪切框架结构所受的南北地震载荷的示意图；
[0057]
图8为本发明实施例提供的算例2中的时间步长取为0.0091s时不同算法获得的位移计算结果对比图；
[0058]
图9为本发明实施例提供的算例2中的时间步长取为0.0153s时不同算法获得的位移计算结果对比图；
[0059]
图10为本发明实施例提供的算例2中的时间步长取为0.001s时不同算法获得的位移计算结果对比图；
[0060]
图11为本发明实施例提供的算例2中的时间步长取为0.001s时不同算法的的位移计算误差的对比图；
[0061]
图12为本发明实施例提供的算例3中的输电塔结构的结构示意图；
[0062]
图13为本发明实施例提供的算例3中的输电塔结构的侧视图；
[0063]
图14为本发明实施例提供的算例3中的输电塔结构的俯视图；
[0064]
图15为本发明实施例提供的算例3中的输电塔结构所受的南北方向地震荷载的示意图；
[0065]
图16为本发明实施例提供的算例3中的不同算法的位移计算误差的对比图。
具体实施方式
[0066]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0067]
本发明的目的是提供一种工程结构振动响应的复合显式时域分析方法及系统，以提高显式时间积分方法的计算精度和计算效率。
[0068]
为使本发明的上述目的、特征和优点能够更加明显易懂，下面结合附图和具体实施方式对本发明作进一步详细的说明。
[0069]
实施例1
[0070]
如图1和图2所示，本发明实施例1提供了本发明提供一种工程结构振动响应的复合显式时域分析方法，所述方法包括如下步骤：
[0071]
步骤101，采用空间单元离散法获取待求解工程结构的动力学控制模型和结构矩阵；所述结构矩阵包括：整体质量矩阵、整体阻尼矩阵和整体刚度矩阵。
[0072]
本发明实施例步骤101属于算法前处理的准备过程，推导得出结构响应的计算公式。
[0073]
确定过程运动方程的具体运算过程：
[0074]
对结构进行有限单元离散，即将结构划分为有限个在结点处相连接的小单元(假设)，然后利用在各单元内假设的形函数来分片逼近全求解域上的未知场函数,即单元e内任一点的位移ai可以用该单元的n个结点位移u
ii
(t)表示：
[0075]ai
(x,y,z,t)＝n1(x,y,z)u
ii
(t)
ꢀꢀꢀ
(1)
[0076]
其中，n1(x,y,z)为单元形函数，它是取决于单元类型的已知函数，将上式写成矩阵形式
[0077]
a＝nueꢀꢀꢀ
(2)
[0078]
其中
[0079]
n＝[n
1 n2…nn
]
ꢀꢀꢀ
(3)
[0080]
式中，a为单元位移场，n为单元形函数矩阵，ue为单元结点位移。
[0081]
则单元应变矩阵为
[0082]
ε＝bueꢀꢀꢀ
(4)
[0083]
其中
[0084]
b＝ln
ꢀꢀꢀ
(5)
[0085][0086]
l为算子矩阵，b为弹性力学几何方程应变与位移关系矩阵，也称应变矩阵。
[0087]
单元应力矩阵为
[0088]
σ＝dbueꢀꢀꢀ
(7)
[0089]
其中
[0090][0091]
其中d为弹性力学物理方程中应力与应变的关系矩阵，也称弹性矩阵，ν为泊松比，e为弹性模量。
[0092]
通过多种方法，如最小势能原理，伽辽金法等，工程结构的内力和外力虚功为
[0093]
[0094]
其中，ke，fe分别为单元刚度矩阵和单元等效结点荷载向量，表示为
[0095]
ke＝∫b
t
dbdveꢀꢀꢀ
(10)
[0096][0097]
又单元结点位移向量可以表示为
[0098]
ue＝geu
ꢀꢀꢀ
(12)
[0099]
其中，u＝[u
11 u
21 u
31
…u1n u
2n u
3n
]
t
为由结构各结点位移组成的结构结点位移向量，n为结构的结点总数，ge为由1和0组成的选择矩阵。如对于平面三角形单元(单元的3个结点的结点号分别为i、j、m)
[0100][0101]
将式(12)带入式(9)中，可得
[0102][0103]
其中，k为整体刚度矩阵，f为结构的总体荷载向量，分别表示为
[0104][0105][0106]
结构的动能为
[0107][0108]
其中，ρ为工程结构密度，为a，ue，u对时间求导结果；m，me分别为工程结构的整体质量矩阵和单元质量矩阵，整体质量矩阵m可由单元质量矩阵me组装而成，可表示为
[0109]
[0110][0111]
粘滞力的虚功为
[0112][0113]
其中，c，ce分别为结构的总体阻尼矩阵和单元阻尼矩阵，表示为
[0114][0115][0116]
哈密顿原理公式为
[0117][0118]
其中，t1～t2为所求工程结构响应的时间间隔
[0119]
将以上各式代入到式(23)中，并进行分部积分，得
[0120][0121]
位移向量u在t1和t2时刻的值是给定的，即考虑到δu的任意性，则有
[0122][0123]
至此获得了结构的运动方程。
[0124]
对于地震响应分析，外力荷载可表示为
[0125][0126]
其中，为地震荷载加速度向量；r为影响向量，它定义了当基础在荷载激励的方
向上产生静态的单位位移时，结构中产生的位移。
[0127]
将式(26)代入到式(25)中，得到地震荷载下结构的运动方程：
[0128][0129]
步骤102，基于所述动力学控制模型和结构矩阵，采用复合显式时间积分法对所述待求解工程结构进行三分步迭代求解，确定振动载荷下所述待求解工程结构在每个整体步的动态响应物理量；所述动态响应物理量包括广义位移矢量、广义速度矢量和广义加速度矢量。
[0130]
由运动方程式(25)可知，要求解有限元系统的位移、速度和加速度矢量，首要步骤是确定有限元系统的质量矩阵、阻尼矩阵、刚度矩阵以及载荷向量。如前所述，逐步时间积分方法还需确定初始广义位移矢量u0、广义速度矢量并由式(25)计算广义加速度矢量对于单自由度系统，上述矩阵和矢量退化为标量。
[0131]
根据具体工程结构的动力学问题类型和算法稳定区间确定时间步长δt；确定5个自由参数p,α,β,r和δ。其中，0《p《1。
[0132]
(1)为获得高计算精度，需限定关系
[0133][0134]
(2)算法的稳定区间求法:解频率方程|k-λm|＝0，可得n个特征根λi(i＝n)，取其中最大值λ
max
，则系统频率最大值稳定区间δt的范围可写为：
[0135][0136]
l为新方法的稳定区间参数，由参数p的取值决定，最大可达到6.0。本算法建议的p值为稳定区间参数为l＝5.508。
[0137]
基于上述初始化之后，步骤102，所述基于所述动力学控制模型和结构矩阵，采用复合显式时间积分法对所述待求解工程结构进行三分步迭代求解，确定振动载荷下所述待求解工程结构在每个整体步的动态响应物理量，具体包括：
[0138]
计算第一分步的广义位移矢量u(t
i+p
)、广义速度矢量广义加速度矢量通过下述公式依次计算：
[0139][0140][0141][0142][0143]
其中，u(t
i+p
)、和分别表示在第i+1个整体步的第一分步的广义
位移矢量、广义速度矢量和广义加速度矢量，u(ti)、和分别表示第i个整体步的广义位移矢量、广义速度矢量和广义加速度矢量，p表示单个的分步占整体步的比例，0《p《1，δt表示整体步的步长，表示第i+1个整体步的第一分步的中间过渡向量，m表示整体质量矩阵，k表示整体刚度矩阵，c表示整体阻尼矩阵，f(t
i+p
)表示第i+1个整体步的第一分步的振动载荷；
[0144]
计算第二分步的广义位移矢量u(t
i+2p
)、广义速度矢量广义加速度矢量通过下述公式依次计算：
[0145][0146][0147][0148][0149]
其中，u(t
i+2p
)、和分别表示在第i+1个整体步的第二分步的广义位移矢量、广义速度矢量和广义加速度矢量，表示复合显式时间积分法中的未知系数向量，f(t
i+2p
)表示第i+1个整体步的第二分步的振动载荷；
[0150]
计算第三分步的广义位移矢量u(t
i+1
)、广义速度矢量广义加速度矢量通过下述公式依次计算：
[0151][0152][0153][0154][0155]
其中，表示第i+1个整体步的中间过渡向量，u(t
i+1
)、)、分别表示第i+1个整体步的广义位移矢量、广义速度矢量和广义加速度矢量，α表示的计算式中的计算比例系数，β表示u(t
i+1
)的计算式中的比例系数，γ和δ分
别表示的计算式中的计算比例系数和的计算比例系数，f
i+1
表示第i+1个整体步的第三分步的振动载荷。
[0156]
为算法迭代递进计算(将当前时刻的结构参数替换初始时刻/上一时刻的结构参数，直到所有时刻的结构参数均被确定后，输出所有结构参数)。将计算得到的结果进行存储，同时通过图2所示的迭代策略对所有时间步进行递进计算与存储，最后得到所有时间点的计算结果，并将其应用于其他物理量的计算与后处理分析。
[0157]
相比目前已商用化应用的cd法和经典的bathe方法，本发明的方法具有更大的稳定区间，更高的精度特性。尤其对于非线性动力学问题，可获得稳定性与计算精度明显更优的计算结果。通过一系列的算例测试验证了新发明方法对于结构响应计算问题求解的有效性、稳定性和高精度特性。三个算例都将新方法与cd法和noh-bathe方法进行对比。下面结合算例、附图和实施过程做进一步说明。每种算法采用相同的时间步长。所有算例的参考解都采用时间步长为δt＝1
×
10-6
s的隐式bathe算法得到。
[0158]
算例1
[0159]
算例1为非线性分析可行性验证的标准算例，主要测试本发明在非线性分析中的可行性、稳定性和计算精度。测试系统如图3所示，该系统为两自由度的弹簧摆。该非线性系统的动力学方程表示为
[0160][0161][0162]
式中，θ表示角位移，r表示径向位移，m表示摆锤的质量，g表示重力加速度，l0表示弹簧未变形时的长度，k表示弹簧的弹性常数。系统的初始条件为
[0163]
r(0)＝r0,θ(0)＝θ0,
[0164]
令m＝1kg，g＝9.81m/s2，l0＝0.5m，ks＝98.1n/m，r0＝0.25m，＝0.25m，和每种算法的时间步长为0.02s。
[0165]
图4给出了径向位移r在0-5s的计算结果。如图所示，与参考解相比，cd法的计算结果出现了较大的偏差，并出现了不收敛的情况，而noh-bathe法和新发明方法的计算结果具有较高的精度。图5给出了径向位移r在200-205s的计算结果。可以看出noh-bathe法的计算结果的误差明显大于新发明方法。总的来说，新发明方法在计算非线性问题中的精度高于cd法和noh-bathe法。
[0166]
算例2
[0167]
算例2为地震响应分析可行性验证的标准基础算例，主要测试本发明的方法在结构动力学问题中的可行性、稳定性和计算精度。如图6所示的十层剪切框架结构受到1940年el centro南北方向地震荷载作用(如图7)。该结构采用层间剪切模型和刚性层假设。采用有限元杆单元离散计算，单元数n＝8,总自由度数为8。所有楼层的初始位移和速度均为0。选取顶层位移进行分析。图8给出了时间步长取为0.0091s时的位移计算结果(时间段0.5-1.5s)。由图8可知，在该时间步长下，cd法的计算结果出现了不收敛的情况，而noh-bathe法
和本发明的方法的计算结果和参考解吻合良好。图9给出了时间步长取为0.0153s时的位移计算结果(时间段0.5-1.5s)。由图9可知，在该时间步长下，noh-bathe法的计算结果出现了不收敛的情况，而本发明方法的计算结果和参考解吻合良好。图10给出了时间步长取为0.001s时的位移计算结果(时间段28-30s)。由图可知，所有计算结果与参考解吻合良好。图11给出了时间步长取为0.001s时的位移误差(时间段29.5-30s)。其中，位移误差e0(t)由下式计算
[0168][0169]
其中，ue(t)为t时刻参考解，u(t)为t时刻计算值。由图可知，新发明方法的计算精度大于cd法和bathe法。综上所述，新发明方法的稳定性和计算精度都好于cd法和bathe法。
[0170]
算例3
[0171]
算例3为验证时间积分方法用于一般结构的计算精度的典型算例，主要测试本发明的方法在工程结构中的可行性和计算精度。如图12所示的输电塔结构受到1971年sanfernando南北方向地震荷载(如图15)的作用。该结构的侧视图和俯视图分别在图13和图14中给出。结构采用三维欧拉-伯努利梁单元。系统的单元总数为249个，单元之间通过刚性节点连接。系统固定在地面上。所有单元的密度为7850kg/m2，弹性模量假定为2
×
107pa，横截面为半径为0.05m的圆形，泊松比为0.2。所有自由度的初始位移和速度均为0。采用时间步长0.001s进行数值模拟。选取a结点在y方向的位移响应进行分析。图16给出了三种方法的位移计算误差(时间段9.5-10s)。由图可知，新发明方法的计算精度高于cd法和noh-bathe法。
[0172]
实施例2
[0173]
本发明实施例2提供一种工程结构振动响应的复合显式时域分析系统，所述系统应用于实施例1的方法，所述系统包括：
[0174]
动力学控制模型和结构矩阵获取模块，用于采用空间单元离散法获取待求解工程结构的动力学控制模型和结构矩阵；所述结构矩阵包括：整体质量矩阵、整体阻尼矩阵和整体刚度矩阵.
[0175]
动态响应物理量迭代求解模块，用于基于所述动力学控制模型和结构矩阵，采用复合显式时间积分法对所述待求解工程结构进行三分步迭代求解，确定振动载荷下所述待求解工程结构在每个整体步的动态响应物理量；所述动态响应物理量包括广义位移矢量、广义速度矢量和广义加速度矢量。
[0176]
本发明实施例2中每个模块的功能的具体实现方式与实施例1的具体步骤相同，在此不再赘述。
[0177]
实施例3
[0178]
本发明实施例3提供一种电子设备，包括存储器、处理器以及存储在所述存储器上并可在所述处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现上述的方法。
[0179]
此外，上述的存储器中的计算机程序通过软件功能单元的形式实现并作为独立的产品销售或使用时，可以存储在一个计算机可读取存储介质中。基于这样的理解，本发明的技术方案本质上或者说对现有技术做出贡献的部分或者该技术方案的部分可以以软件产
品的形式体现出来，该计算机软件产品存储在一个存储介质中，包括若干指令用以使得一台计算机设备(可以是个人计算机、服务器或者网络设备等)执行本发明各个实施例所述方法的全部或部分步骤。而前述的存储介质包括：u盘、移动硬盘、只读存储器、随机存取存储器、磁碟或者光盘等各种可以存储程序代码的介质。
[0180]
实施例4
[0181]
本发明实施例4提供一种计算机可读存储介质，所述存储介质上存储有计算机程序，所述计算机程序被执行时实现上述的方法。
[0182]
根据本发明提供的具体实施例，本发明公开了以下技术效果：
[0183]
本发明采用空间单元离散法获取待求解工程结构的动力学控制模型和结构矩阵；基于所述动力学控制模型和结构矩阵，采用复合显式时间积分法对所述待求解工程结构进行三分步迭代求解，确定振动载荷下所述待求解工程结构在每个整体步的动态响应物理量；本发明采用复合显式时间积分法，并分三步进行迭代求解，克服了现有的显示时间积分法计算非线性问题时的技术缺陷，相比于现有的显式时间积分方法的计算精度和稳定性上都有较大提升。
[0184]
本说明书中各个实施例采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似部分互相参见即可。
[0185]
本文中应用了具体个例对本发明的原理及实施方式进行了阐述，以上实施例的说明只是用于帮助理解本发明的方法及其核心思想；同时，对于本领域的一般技术人员，依据本发明的思想，在具体实施方式及应用范围上均会有改变之处。综上所述，本说明书内容不应理解为对本发明的限制。