一种灌溉机井水电转换系数确定方法与流程

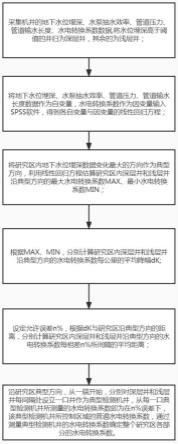
1.本发明属于水电转换系数确定技术领域，具体涉及一种灌溉机井水电转换系数确定方法。


背景技术：

2.农业水资源的科学管理是实现我国水资源高效利用的主要途径之一，随着农业水价综合改革的不断实施，农业用水定额管理取得显著成果，但在农业用水计量、超定额收费等方面推广进度缓慢。
3.现有技术使用传统水表来农业用水计量，然而传统水表计量维护成本高、效率低，易损坏，远传水表虽可以实现数据实时采集等智能化用水管理，但造价较高，且维护、防盗、管理等后期成本较高，使得农业用水始终无法实现精细化管理。
4.针对目前农业用水管理存在的问题，有人提出了“以电折水”计量方法，即通过利用水电之间的转换关系，以耗电量估算机井出水量，不仅能显著提高农业用水的计量效率、降低人工成本，还能为农业用水“以电计水、以电控水、以电管水”的发展思路提供理论支撑，该方法作为一种能较为高效准确的估算用水量的计量方式，具有良好的应用前景。
5.然而如果利用水电转换系数来计量用水量，由于水电转换系数会受到地下水位埋深等因素的影响，各处机井的水电转换系数不尽相同；由于一些区域内的机井数量过多，无法实现测量区域内每一处机井的水电转换系数。
6.总之现有技术存在确定区域水电转换系数困难的问题。


技术实现要素：

7.为了克服上述现有技术存在的不足，本发明提供了一种灌溉机井水电转换系数确定方法。
8.为了实现上述目的，本发明提供如下技术方案：
9.一种灌溉机井水电转换系数确定方法，包括：
10.获取机井的地下水位埋深、水泵抽水效率、管道压力、管道输水长度、水电转换系数数据，将水位埋深高于阈值的井归为深层井，其余的为浅层井；
11.将地下水位埋深、水泵抽水效率、管道压力、管道输水长度数据作为自变量，水电转换系数作为因变量输入spss软件，得到各自变量与因变量的线性回归方程；
12.将研究区内地下水位埋深数据变化最大的方向作为典型方向，利用线性回归方程估算研究区内深层井和浅层井沿典型方向的最大水电转换系数max、最小水电转换系数min；
13.根据max、min，分别计算研究区内深层井和浅层井沿典型方向的水电转换系数每公里的平均降幅dk；
14.设定允许误差n％，根据dk与研究区沿典型方向的距离，分别计算研究区内深层井和浅层井沿典型方向的水电转换系数每相差n％所间隔的平均距离
15.沿研究区典型方向，从一端开始，分别对深层井和浅层井每间隔处设立一口井作为典型监测机井，从每一口典型监测机井所测量的水电转换系数即为在n％误差下，该典型监测机井所控制区域的普遍水电转换系数，通过测量典型监测机井的水电转换系数确定整个研究区各部分的水电转换系数。
16.进一步，所述水电转换系数的计算公式为：
[0017][0018]
其中，k为水电转换系数，q为一时间段内的机井出水流量，e为一时间段内的耗电量。
[0019]
进一步，所述沿典型方向的水电转换系数每公里的平均降幅dk的算法为：
[0020][0021]
其中，s为研究区沿典型方向的距离；
[0022]
进一步，所述沿典型方向的水电转换系数每相差n％所间隔的平均距离其算法为：
[0023][0024]
进一步，所述典型监测机井所控制区域为：沿所述典型方向的相邻两口典型监测机井的连线为边长所构成的正方形区域。
[0025]
进一步，所述线性回归方程为：
[0026]
y＝3.083-0.052x1+3.461x2-0.005x4
[0027]
其中，y为水电转换系数，x1为地下水位埋深，x2为水泵抽水效率，x4为管道输水长度。
[0028]
进一步，所述水泵抽水效率算法为：
[0029][0030]
其中，μ为水泵效率，γ为水的重度，取9.8kn/m3；h为地下水位埋深，p为水泵轴功率，q为水泵出水流量。
[0031]
本发明提供的一种灌溉机井水电转换系数确定方法具有以下有益效果：
[0032]
本发明提出一种在研究区内选取若干典型监测机井，通过检测若干典型监测机井的水电转换系数来掌握全研究区内的水电转换系数的方法；每一口典型监测机井的水电转换系数代表其所控制区域内的普遍水电转换系数，每两口相邻典型监测井的水电转换系数误差为n％,可根据精度需求来选取典型监测机井。解决了现有技术中确定区域水电转换系数困难的问题。
附图说明
[0033]
为了更清楚地说明本发明实施例及其设计方案，下面将对本实施例所需的附图作简单地介绍。下面描述中的附图仅仅是本发明的部分实施例，对于本领域普通技术人员来
说，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。
[0034]
图1为本发明实施例的一种灌溉机井水电转换系数确定方法的结构示意图。
[0035]
图2为本发明实施例的不同地下水位埋深对机井水电转换系数的影响图；
[0036]
图3为本发明实施例的2017年大孔村典型观测井地下水位埋深及水电转换系数变化情况
[0037]
图4为本发明实施例的2017年姚官屯村的典型观测井地下水位埋深及水电转换系数变化情况
具体实施方式
[0038]
为了使本领域技术人员更好的理解本发明的技术方案并能予以实施，下面结合附图和具体实施例对本发明进行详细说明。以下实施例仅用于更加清楚地说明本发明的技术方案，而不能以此来限制本发明的保护范围。
[0039]
实施例：
[0040]
本发明提供了一种灌溉机井水电转换系数确定方法，具体如图1所示，包括：
[0041]
获取机井的地下水位埋深、水泵抽水效率、管道压力、管道输水长度、水电转换系数数据，将水位埋深高于阈值的井归为深层井，其余的为浅层井；将地下水位埋深、水泵抽水效率、管道压力、管道输水长度数据作为自变量，水电转换系数作为因变量输入spss软件，得到各自变量与因变量的线性回归方程；将研究区内地下水位埋深数据变化最大的方向作为典型方向，利用线性回归方程估算研究区内深层井和浅层井沿典型方向的最大水电转换系数max、最小水电转换系数min；根据max、min，分别计算研究区内深层井和浅层井沿典型方向的水电转换系数每公里的平均降幅dk；设定允许误差n％，根据dk与研究区沿典型方向的距离，分别计算研究区内深层井和浅层井沿典型方向的水电转换系数每相差n％所间隔的平均距离沿研究区典型方向，从一端开始，分别对深层井和浅层井每间隔处设立一口井作为典型监测机井，从每一口典型监测机井所测量的水电转换系数即为在n％误差下，该典型监测机井所控制区域的普遍水电转换系数，通过测量典型监测机井的水电转换系数确定整个研究区各部分的水电转换系数。
[0042]
具体的，水电转换系数的计算公式为：
[0043][0044]
其中，k为水电转换系数，q为一时间段内的机井出水流量，e为一时间段内的耗电量。
[0045]
具体的，沿典型方向的水电转换系数每公里的平均降幅dk的算法为：
[0046][0047]
其中，s为研究区沿典型方向的距离；
[0048]
具体的，沿典型方向的水电转换系数每相差n％所间隔的平均距离其算法为：
[0049]
[0050]
具体的，典型监测机井所控制区域为：沿典型方向的相邻两口典型监测机井的连线为边长所构成的正方形区域。
[0051]
具体的，线性回归方程为：
[0052]
y＝3.083-0.052x1+3.461x2-0.005x4；
[0053]
其中，y为水电转换系数，x1为地下水位埋深，x2为水泵抽水效率，x4为管道输水长度。
[0054]
具体的，水泵抽水效率算法为：
[0055][0056]
其中，μ为水泵效率，γ为水的重度，取9.8kn/m3；h为地下水位埋深，p为水泵轴功率，q为水泵出水流量。
[0057]
在本实施例中，利用本发明对河北省7个平原区典型城市的地下水位埋深对水电转换系数的影响进行了研究，并根据研究得出了全省范围内不同允许误差控制目标下机井最优选取情况，具体操作方法如下：
[0058]
1.1监测方案布置
[0059]
通过现场监测以及文案调查等方法，选取河北省沧县境内的113眼农用机井作为主要监测对象，通过监测其单位时间内的单位电量出水量，计算机井水电转换系数。由于所选机井均分布在沧县境内，属于同一区域，机井成机情况基本相同，选取的同一厂家的水泵，保证水泵基本参数一致，同时作物灌溉方式均选取低压管灌，观测中可认为除了地下水位埋深、水泵效率、管道压力和输水管道长度外，其他影响机井水电转换系数的因素水平相当。
[0060]
1.2数据采集及方法
[0061]
为保证试验条件能体现机井实际工作情况，选取农户经常使用的灌溉机井作为典型监测机井，由于系数影响因素较多且不易完全控制，为保证监测试验的可靠性，机井水泵选取同一厂家产品且监测试验在试验区境内同时开展，以确保水泵自身特性以及农村电网等因素间的差异降到最低。随机选取沧县县域内灌溉水源、电力状况及机电设备条件基本一致的113眼农用机井，通过收集相关数据资料开展监测试验。待出水量稳定后，在输水管道上采用手持式超声波流量计测量机井出水量，每个典型监测井至少观测3
ˉ
5个时段，每个时段不少于5min，且保证所测数据均为有效数据。采用测绳对典型灌溉井的地下水位埋深、井深进行测量。机井的耗电量从电表上读取，输水管道长度由卷尺测定，管道系统压力利用普通压力表测定。
[0062]
1.3结果分析
[0063]
1.3.1机井水电转换系数主要影响因素筛选
[0064]
已有研究成果发现，井泵是实现电能转换成出水量的关键设备，也是研究水电转换系数的最重要的影响因素[14]。井泵在抽水时的水量与很多因素有关。为了进一步分析各个因素对水电转换系数的影响程度，本文选择较为容易获取的因素作为主要变量，通过对沧县113眼典型灌溉机井的观测数据为基础，采用spss通径分析法系统分析机井地下水位埋深、水泵效率、管道压力、管道输水长度等因素对河北省机井水电转换系数的影响，并筛选主要影响因素。将数据输入spss并命名各变量，其中，水电转换系数为因变量y，地下水
位埋深、水泵抽水效率、管道压力、管道输水长度分别为自变量x1、x2、x3、x4，数据分析结果如表1所示。从表中可以看出，随着自变量被逐步引入回归方程，回归方程的相关系数r和决定系数r2逐渐增大，说明引入的自变量对水电转换系数的作用在增加。地下水位埋深，水泵效率，管道输水长度与机井水电转换系数之间的相关程度较高，决定系数片2＝0.764，剩余因子因子该值较大，说明对机井水电转换系数有影响的自变量不仅有以上3个方面，仍有部分因素会对系数产生较大影响，但研究并未考虑，故对水电转换系数影响因素的综合分析有待于进一步研究。
[0065]
表1模型概述输出结果
[0066]
tab.1 model overview output results
[0067][0068]
注：a.预测变量：(常量)，地下水位埋深：b.预测变量：(常量)，地下水位埋深，水泵效率：c.预测变量：(常量)，地下水位埋深，水泵效率，管道输水长度。
[0069]
各自变量的偏回归系数、方程截距、标准回归系数(即通径系数)、标准误差以及相对应的显著性检验结果如表2所示，从表中可得线性回归方程为：
[0070]
y＝3.083-0.052x1+3.461x2-0.005x4
[0071]
由通径系数可以看出自变量x1、x2、x4对y的直接作用分别是：p1y＝-0.882、p2y＝0.119、p4y＝-0.103。x1、x2、x4的偏回归系数的显著性均小于0.05，说明自变量与因变量之间存在显著性差异(自变量x3在通径分析过程中已合理剔除)。
[0072]
表2回归系数输出结果
[0073]
tab.2 regression coefficient output results
[0074][0075]
a.因变量：水电转换系数。
[0076]
自变量与因变量、各自变量间的相关系数以及相关检验输出结果如表3所示。从表中可以看出，各自变量之间的相关系数分别是r12＝r21＝0.038，r14＝r41＝-0.165，r24＝r42＝0.047。自变量x1、x2、x4与因变量y之间的简单相关系数分别是，r1y＝-0.861、r2y＝0.080、r4y＝0.047。根据通径分析的理论计算通径系数：r1y＝p1y+r12
×
p2y+r14
×
p4y＝-0.882+(0.038
×
0.119)+
[0077]
(-0.165
×‑
0.103)＝-0.861(结果与表3一致)。
[0078]
表3相关系数及检验输出结果
[0079]
tab.3correlationcoefficientsandtestoutputresults
[0080][0081]
x1通过x2对y的间接通径系数为：r12
×
p2y＝0.038
×
0.119＝0.004522，
[0082]
x1通过x4对y的间接通径系数为：r14
×
p4y＝-0.165
×‑
0.103＝0.016995。同理可以计算出x2、x4对y的间接通径系数。简单相关系数、通径系数及间接通径系数的关系如表4所示。
[0083]
表4简单相关系数的分解
[0084]
tab.4decompositionofsimplecorrelationcoefficients
[0085][0086]
从表4可知，3个自变量对水电转换系数y的直接影响中，地下水位埋深x1的直接作用最大，水泵效率x2次之，输水管道长度x4的直接作用最小。通过分析各个间接通径系数发现，地下水位埋深通过管道输水长度对水电转换系数y的间接作用较大，其间接通径系数r14
×
p4y＝0.022。地下水位埋深通过水泵效率和输水管道长度均能对水电转换系数y产生一定的间接作用(r12
×
p2y＝0.005、r14
×
p4y＝0.017)，从而使地下水位埋深对y的影响较大，二者的简单相关系数r1y达到了-0.861。水泵效率和输水管道长度对y的简单相关系数分别为0.080和0.047，说明水泵效率和输水管道长度会对水电转换系数y产生一定的影响，但其影响不大。
[0087]
1.3.2地下水位埋深与机井水电转化系数相关关系
[0088]
综上可以看出，地下水位埋深x1对水电转换系数的影响具有重要作用，且地下水位埋深与水电转换系数呈负相关关系；至于水泵效率x2和管道输水长度x4，其通径系数均较小，对水电转换系数的改变影响不大，可不必过多考虑(管道压力x3在模型通径分析过程中已剔除)。为了进一步分析地下水位埋深与机井水电转换系数之间的相关关系，基于典型机井监测资料基础上，尽可能保证监测机井水泵效率、管道压力、管道输水长度等因素保持不变，通过收集不同地下水位埋深条件下的监测机井单位时间的出水量与耗电量数据资
料，计算机井水电转换系数，同时，分析地下水位埋深与水电转换系数的偏相关关系，结果如图2所示。从图中可知，地下水位埋深与机井水电转换系数呈负相关关系，决定系数r2＝0.9759，r2越大说明模型拟合程度越好，机井水电转换系数随着地下水位埋深的增大而减少。地下水位埋深与机井水电转换系数之间并不是简单的线性关系，这是由于机井水电转换系数影响因素较多，各个因素均会对系数产生一定影响，结合上文可知，地下水位埋深仅是影响水电转换系数的主要因素，并不是唯一因素，这与前人研究成果一致。
[0089]
2.1获取典型城市地下水位埋深及系数变化情况
[0090]
河北省各地区地下水位埋深分布不均，总体呈“西浅东深”的规律，水位埋深分布的不均导致各地区水电转换系数各不相同，无法采用相同系数估算水泵出水量。若想获得较为准确的机井水电系数，理论上需对全省机井逐一进行抽水试验，通过耗电量和出水量的比值计算水电转换系数。但由于灌溉机井数量众多，大部分相邻机井之间间隔不大，地下水位差距不明显，此时水电转换系数差别不大，若逐一开展监测试验，工程量巨大，成本增加，这无异于会造成资源的浪费。
[0091]
因此，本文采取数学统计方法，通过估算全省7个平原区典型城市的水电转换系数及其单位距离降幅大小，结合全省地下水位埋深及现状机井分布，从地域空间尺度上选择合适数量的灌溉机井作为典型监测机并测算其水电转换系数，系数经过核实、校正无误后传送至周围普通智能机井监测装置，作为该区域内的所有机井的水电转换系数。结果表5、表6所示。
[0092]
表5
[0093]
河北省平原区浅层地下水埋深区机井水电折算系数变化情况
[0094][0095]
表6
[0096]
[0097]
由表5可知，各市浅层水电转换系数变化范围在2.09-6.79m3/kw
·
h之间。由于河北省地下水位埋深整体呈西高东低，结合各市实际控制面积、东西长度距离等因素，计算各市水电转换系数单位公里变化降幅。通过计算，邢台以及石家庄市的水电转换系数较小，但由于其东西长度距离较短，其每公里系数平均降幅较大，约为6.93％-7.89％左右。邯郸市、沧州市次之，每公里系数平均降幅约为8.05％-8.78％，廊坊市、衡水市每公里系数平均降幅最低，仅有3，67％-6.51％，这是由于其全市范围内地下水位埋深变化幅度较小，最大埋深和最小埋深差距不大，使得水电转换系数每公里平均降幅较小，反之亦然。对于深层地下水位埋深区水电转换系数来说，从表6中可以看出，各市水电转换系数明显要低于浅层，由于深层地下水位埋深变化较大，使得最大系数和最小系数相差较大，水电转换系数每公里平均降幅在2.01％-3.08％之间，每公里系数平均降幅明显高于浅层区系数降幅。通过对比发现，保定市的系数最大，为2.97m3/kw
·
h，其次为石家庄市，邢台市的水电转换系数最小，仅为0.62m3/kw
·
h。东西方向上系数每公里平均降幅最大的为石家庄市，降幅为3.65％，其次为保定市，其降幅为3.37％，邢台市系数每公里平均降幅最小，仅有1.83％。
[0098]
2.2监测机井合理布设
[0099]
河北省共有机井986134眼，其中深井168358眼、浅井817776眼。由于水文地质条件、地下水系统及管理要求等影响因素，各市机井分布情况不同。结合上文表1和表2可知，各市每公里系数平均降幅不大，而此时单位面积内机井数量较多，若逐一监测各个机井计算系数，其结果差异不明显，只会造成成本的增加和资源的浪费，不利于经济社会的发展。对此，我们提出可根据相关需求，在一定范围内选择合适数量的灌溉机井作为典型监测井，用某一点的水电转换系数表征附近区域范围内的所有机井的水电转换系数，结果较为准确可靠，同时可显著减轻工作强度，提高测量工作效率。
[0100]
为了进一步确定典型监测机井的合理取设方案，本文结合上文研究成果，设置了5种允许误差控制目标，即当东西方向一定距离下单位电量水泵出水量分别相差1％、2％、3％、4％、5％时，选取典型监测井，并结合分析结果确定全省典型监测机井的空间分布方案，结果如表7所示。
[0101]
表7
[0102]
不同允许误差控制目标下的最优机井选取布局方案
[0103]
tab.7 optimal well selection layout scheme under different allowable error control objectives
[0104][0105]
从表7中可以看出不同允许误差控制目标下的最优浅层机井和深层机井分布规律
相同，监测机井间距和单个机井有效控制面积均是随着允许误差的增大而增大，机井分布密度随着允许误差的增大而减小。并且可以看出衡水市和廊坊市最优浅层机井分布间距以及单个机井控制面积均较大，密度较小，这说明这两市浅层地下水位埋深整体变化不大，使得水电转换系数在较大范围内变化不显著，并且随着允许误差控制目标的增大，典型监测机井控制面积增幅显著，密度降低。邢台市和石家庄市的浅层机井在不同允许误差控制目标下的井间距以及单井控制面积均较小，密度较大，这是由于这两市浅层地下水位埋深变化幅度较大，使得每公里水电转换系数降幅较大，因此应适当增多监测井数量。通过对各市深层监测机井的分布布局方案分析发现，允许误差相同的情况下，廊坊市深层监测机井的选取较为稀疏，密度最小，其次是保定市；邢台市的深层监测机井分布密度最大，需要选取的机井数量最多，允许误差为1％时，每公里需选取2个监测井才能满足允许误差控制目标要求，随着允许误差控制目标的增大，机井分布密度可越来越稀疏。对此我们可根据实际要求选择适宜的监测机井选取方案，进而保证水电转换系数的准确性。诚然，在选取灌溉井作为典型监测井时，应结合现在机井实际分布密度适当调整监测井选取方案。若某一允许误差下的最优监测机井密度要求大于地区机井实际分布密度，说明该地区实际机井数量较少，全部机井均进行抽水试验后获得的水电转换系数仍不能达到允许误差要求，此时需适当增加该区域的机井数量，或者降低允许误差要求。
[0106]
2.3进一步明确全省范围内的监测机井数量
[0107]
通过上文可知，随着允许误差控制目标的增大，相邻监测机井之间距离增大，机井分布越稀疏。为了进一步明确全省范围内的监测机井数量，本研究在7个典型城市机井调查资料的基础上，依据全省机井实际数量及其分布密度情况，确定不同允许误差控制目标下最适宜的监测机井数量，结果如表8、9所示。
[0108]
表8
[0109]
不同允许误差控制目标下浅层机井最优布设量
[0110]
tab.8 optimum layout of shallow motor-driven wells under different allowable error contro ltargets
[0111][0112]
表9
[0113]
不同允许误差控制目标下深层机井最优布设量
[0114]
tab.9 optimal layout of deep wells under difrerent allowable error control targets
[0115][0116]
从表8中可以看出，基于已有机井调查资料上，相同允许误差控制目标下，廊坊市浅层监测机井布设数量最少，其次是衡水市，石家庄市浅层监测机井布设数量最多，这说明石家庄全市范围内浅层地下水位埋深变化较大，使得水电转换系数变化较大，故需适当增加监测机井数量。
[0117]
对于深层机井来说，由于其深层地下水位埋深变化较大，使得每公里水电转换系数降幅较大，故监测机井数量需适当增加。从表9中可以看出，相同允许误差控制目标下，保定市深层监测机井布设数量最少，其次是廊坊市，衡水市的深层监测机井布设数量最多，原因是由于衡水全市范围内深层地下水位埋深变化较大，使得水电转换系数变化较大，故需适当增加监测机井数量。由此可见，监测机井布设数量与地下水位降幅之间关系密切，单位距离地下水位降幅越大的，其水电转换系数变化越明显，为保证农业用水计量的准确性，需适当增加监测机井数量；反之对于单位距离地下水位降幅不大的地区，其水电转换系数变化不明显，可适当增加监测机井间距，在保证计量精度的前提下，减少布设监测井，在减少成本的同时，提高全省机井监测工作效率。
[0118]
结合河北省实际机井数量及其分布情况折算获得全省范围内不同允许误差控制目标下机井最优选取情况，结果如表10所示：
[0119]
表10
[0120]
全省不同允许误差控制目标下机井最优布设量
[0121]
tab.10 optimal layout quantity of motor-driven wells under different allowable error control targets in the province
[0122][0123]
从表10中可以看出，全省浅层机井共817776眼，占到全省机井数量82.93％，深层机井仅占全省机井数量的17.07％。但由于全省浅层地下水位埋深变化幅度较小，使得单位距离水电转换系数变化较小，而深层地下水位埋深变化幅度较大，使得单位距离水电转换系数变化较大，不同允许误差控制目标下浅层监测机井数量明显少于深层监测机井数量，并且随着允许误差控制目标的增大，监测机井数量越来越少。当允许误差控制目标取1％时，仅需对全省范围内的237200眼机井进行监测就可获得全省水电转换系数范围，较逐一
机井测定系数工作量和工作强度减少约75％。随着允许误差的增大，监测机井与全省机井总量的比值越来越小，这说明允许误差越大，监测机井数量越少，监测工作强度越低，效率越高。故为保证全省范围内的水电转换系数的准确性，可根据实际需要选择合适的监测机井布设方案，在满足误差精度要求的前提下，减少监测工作总量，提高工作效率。
[0124]
2.4监测频次合理选取
[0125]
以2017年元氏县大孔观测井和沧县姚官屯观测井的地下水水位埋深变化情况为例，并结合地下水水位埋深与水电转换系数的相关关系模型，计算全年水电转换系数变化情况，结果如图3、图4所示。
[0126]
从图中可以看出，元氏县大孔观测井全年地下水水位埋深在40
ˉ
45m，系数在1.97
ˉ
2.34m3/kw
·
h之间，系数最大降幅为15.60％，最大增幅为18.49％。沧县姚官屯观测井全年地下水水位埋深在58
ˉ
66m，系数在0.99
ˉ
1.31m3/kw
·
h之间，系数最大降幅为24.80％，最大增幅为32.97％。通过调研获悉，现状水电转换系数监测计算通常仅在年内灌溉期前后各1次。由图2可知，年内机井水位受灌溉抽水及降雨补给等因素影响呈动态变化，使得水电转换系数在年内也是随着地下水位埋深的变化而变化，且最大值和最小值之间降幅较大，故建议在年内地下水位下降和水位上升期间分别增加适当的机井监测频次，进而保证系数的准确性。结合上文初步建立了地下水位埋深与水电转换系数之间的相关关系模型，计算分析同一机井年内不同地下水位对应系数的变化情况，根据相关降/增幅变化需求，即当地下水位变幅达到一定水平时，通过增设监测频次等手段保证年内时间尺度上水电转换系数的准确性。
[0127]
本实施例通过建立地下水位埋深与灌溉水电转换系数关联关系，从空间尺度提出了河北省不同地区、深井、浅井机井水泵出水量在计量允许误差分别在1％-5％时，典型机井的东西方向间距、单井控制面积、典型监测井密度等控制性指标，在不降低水电转换系数精度的前提下，根据单位距离水位降幅变化情况选取合适数量的灌溉机井作为典型观测井，实现区域水电转换系数的高效测算。同时根据年内地下水位下降和上升期间相关降/增幅变化需求，通过增设监测频次等手段保证年内时间尺度上水电转换系数的准确性。通过建立全省灌溉机井动态监测机制，合理安排机井监测周期，实现分区、分时监测，尽可能准确估算水电转换系数，从点到面，逐步掌握某一区域水电转换系数变化规律，并根据实际运行情况，不断修正更新，实现全省水电转换系数的精准管控，提高农业用水量的精准计量。
[0128]
以上实施例仅为本发明较佳的具体实施方式，本发明的保护范围不限于此，任何熟悉本领域的技术人员在本发明披露的技术范围内，可显而易见地得到的技术方案的简单变化或等效替换，均属于本发明的保护范围。