一种基于极坐标下补偿线性正则变换的CT图像重构方法

本发明涉及一种ct领域图像重构方法，尤其涉及一种基于极坐标下补偿线性正则变换的ct图像重构方法，属于医学图像信号处理领域。

背景技术：

1、计算机断层成像(ct)技术被公认为20世纪后期最伟大的科技成果之一，它不断给医学诊断带来革命性的影响，还成功地应用于工业无损检测、逆向工程和安全检查等领域。ct主要是利用x射线穿透物体的衰减信息进行重建来获得物体的断层图像信息的技术。所谓断层成像，来源于希腊单词“touos”，表示对物体的横断面进行成像。奥地利数学家radon在1971年发展了abel的思想，使成像对象扩展到任意形状的二维截面。radon提出了投影图像重建的基本数学理论，为ct技术建立了数学理论。由于ct领域的飞速发展,各种各样的信号都具有高速、高加速等特性,并且大都同时具有非平稳、非高斯、非线性等特性。因此,如何通过现代信号处理手段与方法对这些信号进行高效、精细化的分析与处理,如何利用这类信号的特点来解决上述领域中的关键技术问题,已成为现代信号处理领域中所面临的亟待解决的重要问题之一。

2、从理论上讲，ct技术是一个从投影重建图像的反问题，因此重建算法是它的核心理论和基础算法。图像重建算法主要可以分为两类：一类是以radon变换为理论基础的解析类重建算法，另一类是以解方程为主要思想的迭代重建算法。解析类重建算法从radon变换开始，经过几十年的发展，已形成了一套严密和完整的理论体系。根据扫描重建形式的不同，又可以分为二维图像重建和三维图像重建。在二维图像重建算法中，傅里叶中心切片定理是理论基础，基于该定理进行不同的数学变换，可以得到平行束投影下的两种图像重建方法：直接傅里叶重建方法和滤波反投影算法。直接傅里叶重建方法是基于傅里叶中心切片定理的一种最直观的重建算法，也是研究最早的一类算法。但在实际医学图像信号采集过程中，这些信号大部分都是传统傅里叶变换域的非带限信号或者非平稳类信号，运用经典傅里叶重建方法重建ct图像得不到目标图像。其次，由于其因频域插值复杂程度高，只能采集到有限数目的投影，从而仅能获得频域中有限条径向线上的采样点，会造成某些信息缺失，无法在实际中得到广泛应用。另外，以上理论仅限于在傅里叶域，没有在更一般的变换域中得以推广和应用，同时难以在重构中获取信号精细的特征。总的来说，传统的直接傅里叶重建方法在ct领域处处受限，在实际应用中使用较少，因此补偿线性正则变换被引入，弥补直接傅里叶重建方法的不足。

3、补偿线性正则变换是一类具有6个自由参量的线性积分变换，当选取不同的矩阵参数时，它能够转变为传统傅里叶变换、分数阶傅里叶变换和线性正则变换。由于传统傅里叶域的非带限信号有可能是某个角度的补偿线性正则变换域带限信号，因此在工程应用中进行信号处理时，参数的灵活性使得它获得比传统的变换具有更好的特性。但是目前大多数都是基于通常的笛卡尔坐标定义下的补偿线性正则变换理论研究，在解决光声学、计算机断层扫描和磁共振成像等特殊场景下涉及一些通过极坐标自然描述的复杂问题时不太方便。

4、针对一些特殊场景下涉及通过极坐标自然描述的复杂问题和实际医学图像信号采集的大部分都是传统傅里叶变换域的非带限信号或者非平稳类信号问题，目前还没有合适的极坐标系下的变换方法，亟需一种新的ct图像重构算法来解决二维ct图像重建问题。

技术实现思路

1、针对一些通过极坐标自然描述的应用场景下的复杂问题，如计算机断层扫描和磁共振成像等领域，现有ct技术无法较好地处理傅里叶域非带限信号或者非平稳类信号。本发明的主要目的是提出一种基于极坐标下补偿线性正则变换的ct图像重构方法，基于二维补偿线性正则变换中心切片方法，完成目标图像的重构，以多参数形式在ct领域体现了更大的自由度与灵活性，打破实际应用对传统傅里叶域信号带限的要求和限制，减少计算能耗，有效去除ct图像中的环形伪影，获取准确清晰的ct图像。

2、本发明的目的是通过如下技术方案实现的：

3、本发明公开的一种基于极坐标下补偿线性正则变换的ct图像重构方法，通过探测物体的投影数据，计算极坐标系下二维补偿线性正则变换；基于二维补偿线性正则变换中心切片方法，将极坐标系栅格化，二维插值得到笛卡尔坐标系下的二维补偿线性正则变换对应值；最后通过二维逆补偿线性正则变换，完成目标图像的重构。有效去除ct图像中的环形伪影，获取准确清晰的ct图像。

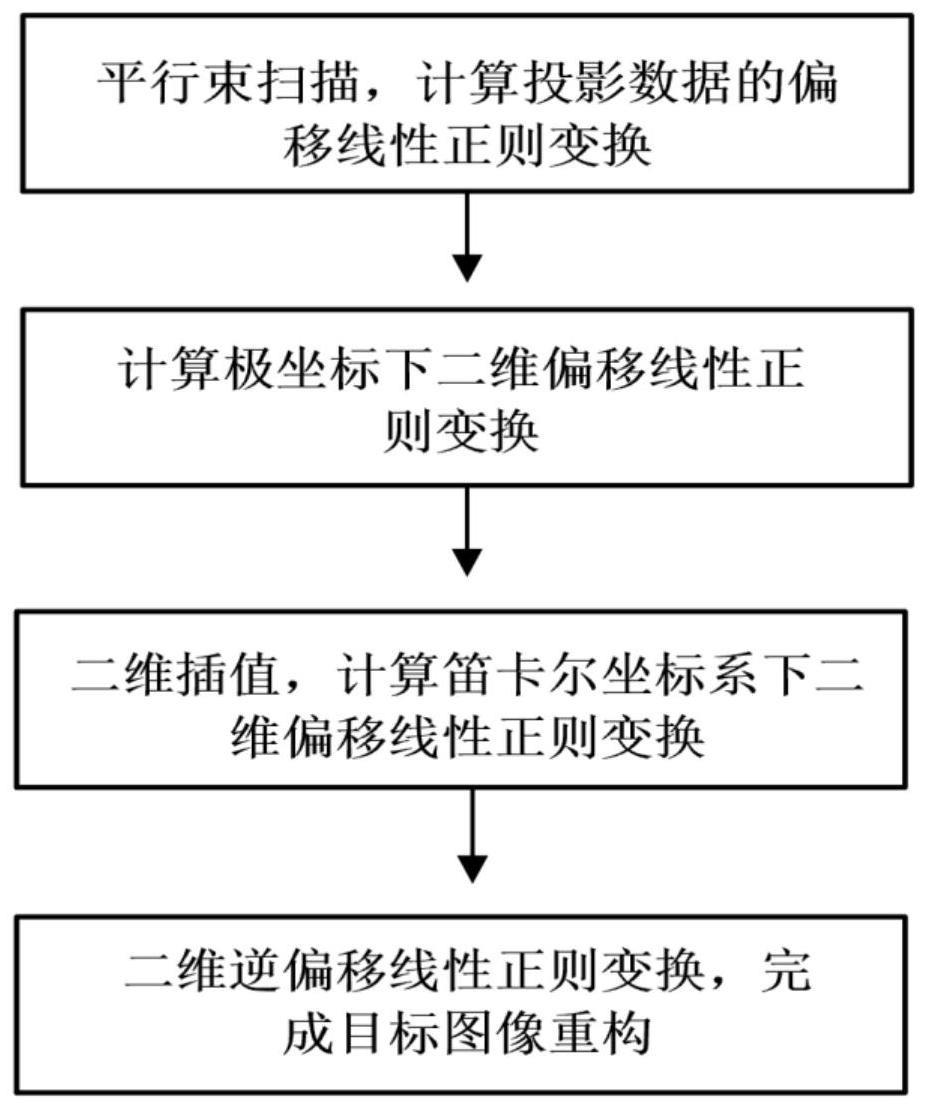
4、本发明公开的一种基于极坐标下补偿线性正则变换的ct图像重构方法，具体包括以下步骤：

5、步骤1、对仿体断层图像进行平行束扫描，获得并显示每个投影角度下的投影数据计算投影数据的一维补偿线性正则变换

6、采用radon变换对原始图像进行平行束扫描，投影角度为0-179度，获得投影数据计算一维补偿线性正则变换此时r和v分别代表投影数据和补偿线性正则频率，

7、

8、其中，是补偿线性正则变换算子，一维补偿线性正则变换参数矩阵m＝(a,b≠0,c,d,u0,w0)，a,b,c,d,u0,满足ad-bc＝1。

9、步骤2、基于二维补偿线性正则变换中心切片方法，计算极坐标系下二维补偿线性正则变换数据

10、为了更好地阐述本专利的步骤二，我们首先给出专利中提出的相关二维变换概念。

11、令t＝(x,y)，w＝(u,v)，t·w＝xu+yv，|t|2＝x2+y2，|w|2＝u2+v2，dt＝dxdy，其中t＝(x,y)为二维信号，x,y分别为时间域变量，u＝(u,v)为对应补偿线性正则频率，u,v分别为补偿线性正则域变量，dt为导数符号。二维信号f(x,y)的补偿线性正则变换在笛卡尔直角坐标系下的表示方法如下：

12、信号f(x,y)关于参数a＝(a,b≠0,c,d)，τ＝(τ1,τ2)和η＝(η1,η2)的二维补偿线性正则变换定义为：

13、

14、其中，是补偿线性正则变换算子，且a,b,c,d,τ1,τ2,η1,满足ad-bc＝1。

15、极坐标系下二维信号f(x,y)的补偿线性正则变换表示公式：

16、令极坐标x＝rcosθ，y＝rsinθ，u＝ρcosφ，v＝ρsinφ。f(r,θ)是以2π为周期的角周期函数且满足dirichlet条件，则以参数a＝(a,b≠0,c,d)，τ＝(τ1,τ2)和η＝(η1,η2)的二维补偿线性正则变换定义为：

17、

18、其中，是补偿线性正则变换算子，a,b,c,d,τ1,τ2,η1,满足ad-bc＝1，并且τ2≠0，dτ2-bη2≠0。

19、在二维图像重建过程中，二维补偿线性正则变换中心切片方法是应用基础，其内容是对物体f(x,y)在角度下得到的旋转坐标系下的平行投影的一维补偿线性正则变换等于在同角度下f(x,y)的二维补偿线性正则变换的一条过原点的直线。

20、因此先要计算极坐标系下二维补偿线性正则变换再通过下列步骤计算得到

21、步骤3、根据极坐标系下的补偿线性正则变换二维插值计算图像在笛卡尔坐标系下二维补偿线性正则变换对应的值。

22、首先根据公式

23、

24、其中(ul,vm)指在笛卡尔坐标系下的采样点，(ρlm,φlm)指对应的极坐标系下的采样点，满足

25、

26、通过二维插值方法将步骤2里的极坐标转化为笛卡尔坐标系下所述计算过程称为“栅格化”。根据不同的模拟数据采用适当的插值算法以防止损失太多的分辨率。

27、步骤4、对步骤3得到的进行二维补偿线性正则变换的逆变换，从而完成目标图像f(x,y)的重构，获得准确清晰的ct图像。

28、根据步骤3得到的笛卡尔坐标系下由信号f(x,y)关于参数a-1＝(d,-b≠0；-c,a)，ξ＝bη-dτ和γ＝cτ-aη的二维补偿线性正则逆变换为

29、

30、其中，是补偿线性正则变换逆算子，ξ,γ为二维实参数向量，从而得到ct领域传统傅里叶域非带限目标图像f(x,y)，获取准确清晰的ct图像。

31、有益效果：

32、1、本发明公开的一种基于极坐标下补偿线性正则变换的ct图像重构方法，采用极坐标下二维补偿线性正则变换表达形式，通过极坐标系，将医学图像中非带限信号或者非平稳类信号的复杂问题简单化，减少计算能耗。

33、2、本发明公开的一种基于极坐标下补偿线性正则变换的ct图像重构方法，应用变换方法的多参数特点在ct领域体现了更大的自由度与灵活性，打破了实际应用对传统傅里叶域信号带限的要求和限制，减少计算能耗，能够有效去除ct图像中的环形伪影，获取准确清晰的ct图像。