一种工程结构的有效分析频段的界定方法及系统

1.本发明涉及统计能量分析技术领域，尤其是一种工程结构的有效分析频段的界定方法及系统。


背景技术：

2.高速列车、运载火箭等工程结构在服役过程中会面临气动噪声、火工冲击等高频振动载荷。统计能量分析理论是预示高频载荷作用下结构动力学响应的常用方法，该方法基于统计物理学原理，将结构划分为若干个子系统，采用振动能量对结构的高频动力学响应和振动载荷进行表征，通过求解子系统间的能量平衡方程来获取结构高频动力学响应。因此，统计能量分析子系统高频段(有效频段)的合理划分是开展统计能量分析的基础和关键。
3.现阶段研究人员大多根据工程经验，依照模态数等对结构子系统高频范围进行划分，一般采用的频率划分方法基于模态数的范围，根据模态数-频率的关系曲线认为模态数大于5以上的频率范围为高频范围。这是一种经验性质的判定，尚没有十分成熟的理论依据可以证明这样的高频段划分下，统计能量分析的结果足够准确。对于工程结构而言，仅通过模态数判断来划分其统计能量分析高频区域时，存在着理论依据不扎实，不能准确判断统计能量分析应用区域是否确实为统计能量分析的有效频段的问题。这会导致后续对复杂结构开展统计能量分析时，结构高频动力学响应预示精度的降低，因此亟需发展一种统计能量分析有效频段的划分方法。


技术实现要素：

4.针对现有技术的不足，本发明提供一种工程结构的有效分析频段的界定方法及系统，解决目前统计能量分析方法中依照模态数直接对结构的高频有效频段进行划分导致划分结果粗糙、不精确的问题。
5.本发明采用的技术方案如下：
6.本技术一方面提供一种工程结构的有效分析频段的界定方法，包括：
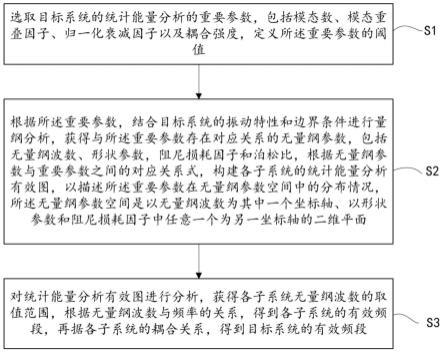
7.选取目标系统的统计能量分析的重要参数，包括模态数ni、模态重叠因子mi、归一化衰减因子以及耦合强度γ
ij
，定义所述重要参数的阈值，其中，下标i代表构成目标系统的子系统的编号，耦合强度γ
ij
用于表征目标系统中任意两个具有耦合作用的子系统i与子系统j之间振动能量的流动强度；
8.根据所述重要参数，结合目标系统的振动特性和边界条件进行量纲分析，获得与所述重要参数存在对应关系的无量纲参数，包括无量纲波数κi、形状参数εi，阻尼损耗因子ηi和泊松比νi，根据无量纲参数与重要参数之间的对应关系式，构建各子系统的统计能量分析有效图，以描述所述重要参数在无量纲参数空间中的分布情况，所述无量纲参数空间是以无量纲波数κi为其中一个坐标轴、以形状参数εi和阻尼损耗因子ηi中任意一个为另一坐标轴的二维平面；
9.对统计能量分析有效图进行分析，获得各子系统无量纲波数的取值范围，根据无量纲波数与频率的关系，得到各子系统的有效频段，再根据各子系统的耦合关系，得到目标系统的有效频段。
10.进一步技术方案为：
11.根据统计能量分析假设条件定义所述重要参数的阈值，包括：
12.模态数n足够大，且n＞＞1；
13.模态重叠因子m＞＞1；
14.归一化衰减因子
15.耦合强度γ＜＜1。
16.所述根据各子系统的耦合关系，得到目标系统的有效频段，包括：
17.根据耦合关系，针对每个子系统的有效频段，进行耦合强度的限定，得到修正的有效频段，将各子系统的修正的有效频段取交集后作为目标系统的有效频段。
18.所述重要参数与无量纲参数之间的对应关系包括：
[0019][0020][0021][0022][0023]
νi＝νi[0024]
式中，下标i代表构成目标系统的子系统的编号，τ
ij
代表传输效率，l
ij
为子系统i与子系统j之间的耦合长度，pi为子系统i的周长。
[0025]
所述无量纲波数与频率的关系通过下式获得：
[0026]
dk
4-ρhω2＝0
[0027]
其中，k、e、h、ρ、ν、ω分别为波数、弹性模量、厚度、密度、密度、泊松比和圆频率，波数k＝2πκ/l，κ为无量纲波数，l为与结构相关的尺寸参数。
[0028]
对统计能量分析有效图进行分析时，形状参数εi可以设置为一个固定值。
[0029]
对统计能量分析有效图进行分析时，阻尼损耗因子ηi可以设置为一个固定值。
[0030]
本技术另一方面提供一种工程结构的有效分析频段的界定系统，包括：
[0031]
选取模块：选取关于目标系统统计能量分析的重要参数，包括模态数ni、模态重叠因子mi、归一化衰减因子以及耦合强度γ
ij
，定义所述重要参数的阈值，其中，下标i代表构成目标系统的子系统的编号，耦合强度γ
ij
用于表征目标系统中任意两个具有耦合作用的子系统i与子系统j之间振动能量的流动强度；
[0032]
建图模块：根据所述重要参数，结合目标系统的振动特性和边界条件进行量纲分析，获得与所述重要参数存在对应关系的无量纲参数，包括无量纲波数κi、形状参数εi，阻尼损耗因子ηi和泊松比νi，根据无量纲参数与重要参数之间的对应关系式，构建各子系统的统计能量分析有效图，以描述所述重要参数在无量纲参数空间中的分布情况，所述无量纲参
数空间是以无量纲波数κi为其中一个坐标轴、以形状参数εi和阻尼损耗因子ηi中任意一个为另一坐标轴的二维平面；
[0033]
分析模块：对统计能量分析有效图进行分析，获得各子系统无量纲波数的取值范围，根据无量纲波数与频率的关系，得到获得各子系统的有效频段，根据各子系统的耦合关系，得到目标系统的有效频段。
[0034]
本发明的有益效果如下：
[0035]
本发明从统计能量分析的基本假设出发，依据量纲分析，获取了无量纲参数空间下统计能量分析有效图，根据有效图和结构子系统参数即可推出结构子系统在保证统计能量分析有效的前提下划分的有效频段范围，从而弥补了现有频段划分方法的不足。
[0036]
本发明划分频段方法快速、直观、准确，有助于提高工程结构高频动力学响应预测精度。
[0037]
本发明的其它特征和优点将在随后的说明书中阐述，并且，部分地从说明书中变得显而易见，或者通过实施本发明而了解。
附图说明
[0038]
图1为本发明方法的流程图。
[0039]
图2为本发明实施例的耦合板结构的结构示意图。
[0040]
图3为本发明实施例的子系统二的η-κ平面统计能量分析有效图。
[0041]
图4为本发明实施例的子系统二的ε-κ平面的统计能量分析有效图。
[0042]
图中：1、子系统一；2、子系统二；3、子系统三。
具体实施方式
[0043]
以下结合附图说明本发明的具体实施方式。
[0044]
本技术提供一种工程结构的有效分析频段的界定方法，包括：
[0045]
参见图1，选取目标系统的统计能量分析的重要参数，包括模态数ni、模态重叠因子mi、归一化衰减因子以及耦合强度γ
ij
，定义所述重要参数的阈值，其中，下标i代表构成目标系统的子系统的编号，耦合强度γ
ij
用于表征目标系统中任意两个具有耦合作用的子系统i与子系统j之间振动能量的流动强度；
[0046]
根据所述重要参数，结合目标系统的振动特性和边界条件进行量纲分析，获得与所述重要参数存在对应关系的无量纲参数，包括无量纲波数κi、形状参数εi，阻尼损耗因子ηi和泊松比νi，根据无量纲参数与重要参数之间的对应关系式，构建各子系统的统计能量分析有效图，以描述所述重要参数在无量纲参数空间中的分布情况，所述无量纲参数空间是以无量纲波数κi为其中一个坐标轴、以形状参数εi和阻尼损耗因子ηi中任意一个为另一坐标轴的二维平面；
[0047]
对统计能量分析有效图进行分析，获得各子系统无量纲波数的取值范围，根据无量纲波数与频率的关系，得到获得各子系统的有效频段，根据各子系统的耦合关系，得到目标系统的有效频段。
[0048]
本技术方法针对的目标系统是由多个子系统耦合而成，或者说将目标系统划分为若干个子系统，基于统计能量分析的基本假设得到统计能量分析中重要参数的范围，并在
无量纲参数空间中将统计能量分析的有效区域采用图像的方式表示出来，形成统计能量分析有效图，可以根据结构子系统的参数和有效图确定高频区域的范围。
[0049]
本技术方法从统计能量应用的理论假设出发，得到统计能量分析结果准确的范围，而不单单采用以往以模态数为标准的频率划分，所得统计能量分析的高频范围结果更精确。
[0050]
具体的，根据统计能量分析假设条件定义所述重要参数的阈值，包括：
[0051]
模态数n足够大，且n＞＞1；
[0052]
模态重叠因子m＞＞1；
[0053]
归一化衰减因子
[0054]
耦合强度γ＜＜1。
[0055]
统计能量分析假设条件的原理具体如下：
[0056]
(1)在统计能量分析中，能量储存在大量模态中，但模态数远小于阿伏伽德罗常量(6.02
×
10
23
)，所以统计能量分析是一种适用于小群体的统计方法，其相对方差(方差除以平均值的平方)的数量级为log(n/n2)，要保证误差足够小，需模态数足够大，本技术定义n＞＞1，即模态数远远大于1；
[0057]
(2)统计能量分析是对非相干振动能的研究，无序性是统计方法的固有特性，而振动中的无序性意味着，被视为随机变量的模态振幅是不相关的。当没有模态主导系统动力学时，即频率响应函数平滑时达到该状态。模态重叠因子是描述频率响应函数中连续模态重叠程度的参数，统计能量分析在统计上具有无序性的标准是m＞＞1，即模态重叠因子远大于1；
[0058]
(3)统计能量分析的子系统的任何点的振动能量密度是均匀的和各向同性的(漫反射场假设)。为了达到这种平衡状态，归一化衰减因子必须足够低以确保射线在衰减之前穿过子系统多次，即即归一化衰减因子远远小于1；
[0059]
(4)与能量的内部耗散相比，子系统之间交换振动能量的流动很小(弱耦合假设)。也就是说耦合损耗因子远小于内损耗因子，耦合强度定义为γ
ij
＝η
ij
/ηi，ηi、η
ij
分别代表子系统i的阻尼损耗因子和考虑与子系统j耦合后的子系统i的阻尼损耗因子。其中，对于一般由板状单元耦合成的目标系统，各板状单元之间的耦合强度γ
ij
＜＜1。
[0060]
所述重要参数与无量纲参数之间的对应关系包括：
[0061][0062][0063][0064][0065]
νi＝νi[0066]
式中，下标i代表构成目标系统的子系统的编号，τ
ij
代表传输效率，l
ij
为子系统i与子系统j之间的耦合长度，pi为子系统i的周长。
[0067]
根据上述的对应关系，可以对每个子系统建立统计能量分析有效图，基于前述的假设条件，以及其他参数的限定，可直接获得无量纲波数的范围，最终获得考虑了耦合强度
的整个目标系统的有效频段范围。
[0068]
以下以具体实施例进一步说明本技术的工程结构的有效分析频段的界定方法。
[0069]
参见图2，本实施例针对的目标系统的结构为耦合板结构，其包括三个子系统，子系统一1、子系统二2和子系统三3，三个子系统均为矩形板状结构且顺次相接形成耦合关系，子系统二2两侧分别与子系统一1和子系统三3相连，每个板的尺寸相同、材料相同，长宽边长均为300mm,厚度均为2mm。
[0070]
材料参数为：弹性模量为102gpa，密度为2000kg/m3，泊松比为0.2。
[0071]
重要参数中：传输效率τ
ij
在弱耦合假设条件下，可以取值为1。子系统i的周长pi即为1200mm。
[0072]
无量纲参数中：形状参数b为耦合边长即具有耦合关系的两个板之间的连接边的边长，ai为板宽，可知本实施例中b与a均为300mm；无量纲波数κi＝kili/2π，l为与结构相关的尺寸参数，k为波数，l＝πaib/2(ai+b)＝0.23562。
[0073]
由于本实施例的耦合关系简单，子系统二2和其他两个子系统均存在耦合关系，因此首先可根据子系统二2的无量纲参数与重要参数的对应关系构建其统计能量分析有效图，如图3和图4所示。图3和图4所示是横坐标为无量纲波数、纵坐标分别为阻尼损耗因子和形状参数的无量纲空间下的统计能量分析有效图。可根据实际情况择一使用。
[0074]
阻尼损耗因子可取一个固定值为0.01，形状参数对于尺寸确定的耦合板系统是固定的，且由于是矩形板，形状参数一定大于1，根据板的尺寸，形状参数为定值1.1284，所以无量纲波数在图4中被限制在m＝1和之间的一条与横坐标平行的横线段ac上，由此可以得到子系统二2的无量纲波数的范围κ∈(4.431,31.831)。
[0075]
然后根据无量纲波数与频率的关系，可以得到相应的频段范围：
[0076]
无量纲波数与频率的关系通过下式获得：
[0077]
dk
4-ρhω2＝0
[0078]
其中，k、e、h、ρ、ν、ω分别为波数、弹性模量、厚度、密度、密度、泊松比和圆频率。
[0079]
然后，根据即可获得相应的频段范围。
[0080]
本实施例中，由于板结构尺寸材料一样，耦合关系简单。可以在计算出子系统二2的无量纲波数的范围κ∈(4.431,31.831)后，直接根据耦合关系对其进行修正，得到修正后的无量纲波数范围，即为目标系统的无量纲波数范围，然后再换算成频率得到目标系统的有效频段，具体包括：
[0081]
考虑耦合关系，由于耦合强度小于1，可以得出子系统二2在和子系统一1耦合下的无量纲波数范围：κ＞7.958，并且，子系统二2在和子系统三3耦合下的无量纲波数范围：κ＞7.958，于是无量纲波数被限制在图4中的线段bc上，综合可得子系统2的无量纲波数范围κ∈(7.958,31.8，根据波数和无量纲波数的关系k＝2πκ/l，l＝πab/2(a+b)，l＝0.23562，可以得到子系统2波数的范围k∈(118.16,848.83)于是可以得到子系统二2波数的范围k∈(212.21,848.83)。
[0082]
根据频率和波数的关系dk
4-ρhω2＝0，得到圆频率：其中，h、ρ取值已知。再根据耦合板结构(目标系统)的统计能量分析有效频段为f∈(9537.46,482551.17)，单位为hz。
[0083]
对于本实施例的目标系统，由于耦合关系简单子系统数量少，子系统由于尺寸一致，可以子系统二2为基础，结合其余其他子系统的耦合关系，在其统计能量分析有效图中通过耦合强度对有效频段进行进一步限定，即可得到耦合板结构的统计能量分析有效频段。对于不确定形状参数和阻尼损耗因子的系统则可以使用图3进行分析。
[0084]
本领域技术人员可理解，对于复杂结构的目标系统，例如子系统的结构尺寸不一样、或者子系统数量较多、耦合关系多时，需要分别获得每个子系统的能量分析有效图(参见图3或图4的形式)，然后获得子系统的无量纲波数范围及对应的频段范围，再根据耦合情况，对于每一种耦合关系都根据尺寸参数、通过耦合强度进行限定，进一步修正所得的频段范围，对于所得的不同的子系统的修正后的频段范围，可通过求取交集的方式获得最终的频段范围，作为目标系统的有效频段。
[0085]
本技术还提供一种工程结构的有效分析频段的界定系统，包括：
[0086]
选取模块：选取关于目标系统统计能量分析的重要参数，包括模态数ni、模态重叠因子mi、归一化衰减因子以及耦合强度γ
ij
，定义所述重要参数的阈值，其中，下标i代表构成目标系统的子系统的编号，耦合强度γ
ij
用于表征目标系统中任意两个具有耦合作用的子系统i与子系统j之间振动能量的流动强度；
[0087]
建图模块：根据所述重要参数，结合目标系统的振动特性和边界条件进行量纲分析，获得与所述重要参数存在对应关系的无量纲参数，包括无量纲波数κi、形状参数εi，阻尼损耗因子ηi和泊松比νi，根据无量纲参数与重要参数之间的对应关系式，构建各子系统的统计能量分析有效图，以描述所述重要参数在无量纲参数空间中的分布情况，所述无量纲参数空间是以无量纲波数κi为其中一个坐标轴、以形状参数εi和阻尼损耗因子ηi中任意一个为另一坐标轴的二维平面；
[0088]
分析模块：对统计能量分析有效图进行分析，获得各子系统无量纲波数的取值范围，根据无量纲波数与频率的关系，得到获得各子系统的有效频段，根据各子系统的耦合关系，得到目标系统的有效频段。
[0089]
本领域普通技术人员可以理解：以上所述仅为本发明的优选实施例而已，并不用于限制本发明，尽管参照前述实施例对本发明进行了详细的说明，对于本领域的技术人员来说，其依然可以对前述各实施例记载的技术方案进行修改，或者对其中部分技术特征进行等同替换。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。