一种区域能源系统中的能量站选址方法

1.本发明涉及能源系统规划技术领域，尤其是涉及一种区域能源系统中的能量站选址方法。


背景技术：

2.当前智能电网发展有着不同的发展侧重点，未来能源网的结构在不同地区会根据当地的地理环境和不同的可再生能源资源发生改变，因此会展现出不同拓扑特征的网络结构，未来的工作会根据现有各不同国家和地区的智能网络发展特点，拓展参数设置，以生成具有不同发展特点的能源互联网拓扑模型。
3.能量站选址，通过能源站实现多种能源相互耦合与转换，能源站间协调互补，实现能源的优化利用，构建未来的区域综合能源系统，提高区域的能源利用效率、改善系统运行的经济性以及增加多能消纳的途径，打破传统的单一规划和独自运行的模式有效提高能源使用效率，具有良好的经济效益与环境效益。
4.中国专利cn111582658b公开了考虑多区域互联协同的能源站设备配置及管线规划方法，该方法以多区域系统总成本最低为目标建立模型时，只机械的考虑了前期的设备投资费用，后期运行成本未进行考虑，现有技术未考虑能量站规划对环境影响，忽略了环境成本，求得的结果经济性误差较大。


技术实现要素：

5.本发明的目的就是为了克服上述现有技术存在的缺陷而提供一种区域能源系统中的能量站选址方法。
6.本发明的目的可以通过以下技术方案来实现：
7.一种区域能源系统中的能量站选址方法，所述方法包括以下步骤：
8.应用赋权图g＝{v,e,w}来描述能量站网络的图论模型；
9.以从n个能量站候选节点选择p个最优的能量站节点来满足用户负荷需求，使得两者之间的赋权距离最短，整合能量传输管线和能量站建设造价，总成本最小为目标，建立基于p-中位选址模型；
10.采用改进枚举法求解选址模型，得到选址结果；
11.所述采用改进枚举法求解选址模型包括以下步骤：
12.构建能量站网络模型g的最小权重矩阵d和最短路径矩阵l；
13.从负荷节点m出发，依据最小权重矩阵d，计算p-中位选址模型，选择权重更小的能量站，循环枚举最后得到权重最小的能量站；
14.输出权重最小能量站的能量站数量、选址和管道路径。
15.作为优选技术方案，所述应用赋权图g＝{v,e,w}来描述能量站互联网的图论模型为：
16.节点集合v＝m∪n∪q，m＝{m|m＝1,2,
…
m0}为负荷中心集合，n＝{n|n＝1,2,
…
n0}
为候选能源站集合，q＝{q|q＝1,2,
…
q0}为路网结点集合，且m、n和q为两两不相交集合；边矩阵e＝{e(i,j)|i,j∈v}，表示节点集合v中节点i和节点j之间的直接连通关系；权重矩阵w＝{w(e(i,j))＝w(i,j)|e(i,j)∈v}，表示e(i,j)的权重；
17.所述边矩阵e表达式为：
[0018][0019]
式中：e(i,j)∈e i，j∈v；
[0020]
所述权重矩阵w表达式为：
[0021][0022]
式中w(i,j)为w的元素；i，j∈v；c
ep,ij
为节点集合v中节点i到节点j输电管网的造价；c
hp,ij
为节点i到节点j供热管网投资费用。
[0023]
作为优选技术方案，所述节点集合v中节点i到节点j输电管网的造价c
ep,ij
包括电缆材料费用和电缆隧道建设费用，表达式为：
[0024]cep,ij
＝(c
ep,line,ij
+c
ep,pipe,ij
)l
ep,ij
[0025]
式中：c
ep,line,ij
为节点i到节点j输电管网电缆材料单价；c
ep,pipe,ij
为节点i到节点j输电管网电缆隧道单价；l
ep,ij
为输电线路长度；
[0026]
所述节点i到节点j供热管网投资费用c
hp,ij
包括管网材料费用、管网通道建设费用和土建费用：表达式为
[0027]chp,ij
＝f(d
hp,ij
)l
hp,ij
[0028]
f(d
hp,ij
)＝9.606d
hp,ij-873.15
[0029]
式中：c
hp,ij
为节点i到到节点j供热管网的投资费用；d
hp,ij
为节点i到到节点j供热管网管径；f(d
hp,ij
)表示节点i到到节点j供热管网单位长度造价；l
hp,ij
为节点i到到节点j供热管网长度。
[0030]
作为优选技术方案，所述基于p-中位的选址模型为：
[0031][0032][0033]
xn,y
mn
∈{0,1}
[0034]
式中，p
ld，m
为负荷节点m的负荷需求；c
es，n
为能量站n的建设费；d
mn
表示负荷节点m到能量站n的最短距离；p是待选能量站，xn表示待选能量站p是否被选中，若p被选中，则xn为
1，否则xn为0；y
mn
表示负荷节点m能否由能量站n供能，若能供能，则y
mn
为1，否则y
mn
为0。
[0035]
作为优选技术方案，所述负荷节点m的负荷需求p
ld，m
表示为：
[0036][0037]
式中，为负荷节点m的电能需求，若需要，否则
[0038]
为负荷节点m的热能需求，若需要，否则
[0039]
为负荷节点m的电负荷；为负荷节点m的热负荷。
[0040]
作为优选技术方案，所述能量站n的建设费c
es，n
表达式为：
[0041][0042]
式中，c
es，n
为能量站的建设费；为能源站初始投资费用；r为利率，l为管线寿命年限；为能源站年维护管理费用；c
env
为环境成本。
[0043]
作为优选技术方案，所述能源站n的初始投资费用包括土建费用、设备投资安装费用和运行维护费用，表达式为：
[0044][0045]
式中：p
el,n
为能量站n提供的电负荷；p
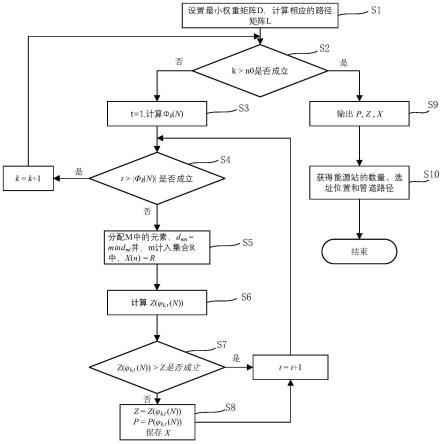
hl,n
为能量站n提供的热负荷；c
es，n
为满足负荷需求的能量站设备的单位容量投资成本；
[0046]
所述能源站n的年维护管理费用包括人工费和维护费，其表达式为：
[0047][0048]
式中，为能源站年维护管理费用；ζ1为人工费用比例系数；ζ2为维护费用比例系数；为能源站初始投资费用。
[0049]
作为优选技术方案，所述环境成本c
env
表达式为：
[0050][0051]
其中，π
ctax
为碳税；ef为燃烧天然气排放co2的碳排放强度；为t时刻能源站n的燃气消耗量；e
grid
为与大电网的购电排放co2的碳排放强度；η
grid
为电网传输效率；为t时刻能源站n与大电网的购电功率。
[0052]
作为优选技术方案，所述构建最小权重矩阵d和最短路径矩阵l为：
[0053]
采用dijkstra算法求解区域综合能量站网络g各顶点间的最小权重，根据下面计算方法求解最小权重矩阵d；
[0054][0055]
式中d
ij
为d的元素；i，j∈v；d
ij
表示节点i和节点j之间的的最小权重；记l(i,j)表示当顶点i和j取得最小权重时，二者之间的路径，记录取得最小权重时两顶点间的路径矩阵l，l(i,j)∈l，l为s
×
s阶矩阵，其中s＝|v|。
[0056]
作为优选技术方案，所述从负荷节点m出发，计算p-中位选址模型，选择权重更小的能量站，循环枚举最后得到权重最小的能量站的具体流程如下：
[0057]
m表示负荷节点集合，n表示候选能源站集合，令ψ(n)表示集合n的幂集，表示幂集ψ(n)中所有含k个元素的子集组成的集合；表示中第o个元素，有z表示目标函数值，p表示中位点集合，x＝{xo|o＝1,2
…
}表示能量站供给用户负荷的分配情况，即x1表示第一个能量站供给的用户负荷的集合，令k＝1；z
→
∞；集合p，x和l均为空集；
[0058]
步骤1：判断k是否大于待选能量站个数，如果是转至步骤7；若否则进入步骤2；
[0059]
步骤2：令t＝1，计算
[0060]
步骤3：判断若是，令k＝k+1后转至步骤1；若否，进入步骤4；
[0061]
步骤4：定义r为空集，对于给定m∈m，计算d
mo
，其中，记最小权重d
mn
＝min(d
mo
)，则将m记入集合r中，并令x(n)＝r；重复计算，直至m中的元素全部分配；
[0062]
步骤5：令目标函数计算目标函；
[0063]
步骤6：判断若是，令若是，令保存x，令t＝t+1，执行步骤3；若否，令k＝k+1，转到步骤2；
[0064]
步骤7：输出p，z，x。
[0065]
与现有技术相比，本发明具有以下有益效果：
[0066]
1)本发明提供了一种改进枚举法求解，从用户负荷节点m出发，考虑传输距离递增顺序，选择权重较小的能量站，循环枚举逐渐得到最短路径为其传输能量。依据拓扑网络和模型特点，相较于传统枚举法减小了不必要的计算量，提高了计算效率。
[0067]
2)本发明采用的改进p-中位模型进行选址，综合考虑前期的设备投资费用，后期运行成本以及环境成本，模型更加具现实意义，求得的结果经济性误差较小。
[0068]
3)本发明根据用能区域负荷分布情况以及用户对能源的需求，基于p-中位模型，在规划层面，对能量站数量、位置、供能网络路径布局，以及综合能量站－网配置进行优化，同时联合系统运行优化，使系统各时刻调度最优。
[0069]
4)本发明在考虑管线路径权重时，以沿着交通道路布设管线为最短铺设路径，节省区域的地下空间，降低了频繁开挖路面对生活的影响，实现热、电综合管廊且路径一致。
附图说明
[0070]
图1为本发明采用改进枚举法求解p-中位选址模型的流程示意图；
[0071]
图2为本发明实施例中南方某园区能量系统节点示意图；
[0072]
图3为本发明对实施例中某园区能量系统节点进行选址后的能量站选址和传输路径示意图。
具体实施方式
[0073]
下面结合附图和具体实施例对本发明进行详细说明。本实施例以本发明技术方案为前提进行实施，给出了详细的实施方式和具体的操作过程，但本发明的保护范围不限于下述的实施例。
[0074]
通常，首先把能量站和负荷用户看作区域内的各个网络节点，能量输送的管网路径看作网络中的边，结合环境、经济等因素，在众多的待选节点中选择一个或者p个合适的网络节点，在这些节点位置上建设能量站达到与负荷用户实现能量传输，这就是能量站的位置选址可以转化为“点”和“边”所构成的数学问题，在借助图论的方法进行求解。p-中位问题就是能源网络中公共设施选择位置问题中常见的问题，通过p-中位模型进行选址的优势在于，其所构建的模型多为线性优化模型，相比较非线性优化，线性优化模型具有求解速度和求解精度多方面的优势。
[0075]
考虑区域综合能量系统的规划建设，往往为了节省区域的地下空间，降低频繁开挖路面对生活的影响，所以工程管线铺设路径一般沿着交通道路的边缘进行，实现热、电综合管廊且路径一致。应用赋权图g＝{v,e,w}来描述区域能量系统中的能量站、能量传输管网和用户负荷的规划选择，顶点集v则由用户负荷节点、待选能量站和道路网节点形成，边集e表示各顶点间的直接连通状况，权集w表示各顶点能量输送管网的以及能量站造价成本。
[0076]
定义m＝{m|m＝1,2,
…
m0}为负荷节点集合，n＝{n|n＝1,2,
…
n0}为候选源站节点集合，q＝{q|q＝1,2,
…
q0}为路网节点集合，则v＝m∪n∪q,其中，m，n和q为两两不相交集合；边集e＝{e(i,j)|i,j∈v}，表示节点集合v中节点i和节点j之间的直接连通关系；权重集w＝{w(e(i,j))＝w(i,j)|e(i,j)∈v}，表示e(i,j)的权重。
[0077]
式中，边的权重式中，边的权重储输电线路(vi,vj)的距离；输送容量。节点权重集w
vi
＝{c
ep,ij
,c
hp,ij
,c
es,n
}存储投资费用，即c
ep,ij
输电管网投资费用、c
hp,ij
供热管网投资费用和能量站综合造价。
[0078]
定义负荷节点m的负荷需求p
ld，m
具体表示：
[0079][0080]
式中，为负荷节点m的电能需求，若需要，否则
[0081]
为负荷节点m的热能需求，若需要，否则
[0082]
为负荷节点m的电负荷；为负荷节点m的热负荷；
[0083]
节点i和j之间的传输线路造价具体表示：
[0084][0085]
式中，为负荷节点m的电能供应，若需要，否则
[0086]
为负荷节点m的热能供应，若需要，否则
[0087]
为结点i和和j之间的输电线路造价；为结点i和和j之间的供热管网造价。
[0088]
在区域综合能源系统能量站选址过程中，随着确定选址的能量站数量和能量站总负荷的增加，能量站的建设总造价也会变化，因此，在目标函数的优化中需考虑能量站的造价费用。某一能量站n综合造价c
es，n
可以表示为
[0089][0090]
式中，c
es，n
为能量站的建设费；为能源站初始投资费用；r为利率，l为管线寿命年限；为能源站年维护管理费用；c
env
为环境成本。
[0091]
综上定义，区域综合能源系统能量站的优化规划问题可以总结为:在区域范围内，存在着集合m个能量站候选节点，集合n个用户负荷节点。通过计算从m个能量站候选节点选择p个最优的能量站节点来满足用户负荷需求，使得两者之间的赋权距离最短，整合能量传输管线和能量站建设造价，以总成本最小为目标进行建模。改进p-中位模型可以表示为：
[0092][0093][0094]
xn,y
mn
∈{0,1}
[0095]
式中，d
mn
是负荷节点i到能量站j的最短距离；p是待选能量站，若p被选中，则xn为1，否则xn为0；y
mn
是指节点m能否由能量站n供能，若可以供能，则y
mn
为1，否则y
mn
为0。
[0096]
输电管网造价模型：
[0097]
输电管网的造价包括电缆材料费用和电缆隧道建设费用，节点i到节点j输电管网的造价c
ep,ij
表示为：
[0098]cep,ij
＝(c
ep,line,ij
+c
ep,pipe,ij
)l
ep,ij
[0099]
式中：c
ep,line,ij
为节点i到节点j输电管网电缆材料单价；c
ep,pipe,ij
为节点i到节点j输电管网电缆隧道单价；l
ep,i
j为输电线路长度。
[0100]
供热管网造价费用模型：
[0101]
供热管网投资费用包括管网材料费用和管网通道建设费用，节点i到节点j供热管网投资费用(包括土建费用)c
hp,ij
表示为：
[0102]chp,ij
＝f(d
hp,ij
)l
hp,ij
[0103]
f(d
hp,ij
)＝9.606d
hp,ij-873.15
[0104]
式中：c
hp,ij
为节点i到节点j供热管网的投资费用；d
hp,ij
为节点i到节点j供热管网管径；f(d
hp,ij
)为节点i到节点j供热管网单位长度造价；l
hp,ij
为节点i到节点j供热管网长度。
[0105]
能量站初始投资费用：
[0106]
区域综合能源系统能量站造价包括土建费用、设备投资安装费用和运行维护费用，某一能量站初始投资费用示为:
[0107][0108]
式中：p
el,n
为能量站n提供的电负荷；p
hl,n
为能量站n提供的热负荷；c
es，n
为满足负荷需求的能量站设备的单位容量投资成本。
[0109]
能量站年维护管理费用
[0110]
能量站年维护管理费用，主要包括人工费和维护费：
[0111][0112]
式中，为能源站年维护管理费用；ζ1为人工费用比例系数；ζ2为维护费用比例系数；为能源站初始投资费用。
[0113]
环境成本：
[0114][0115]
其中，π
ctax
为碳税；ef为燃烧天然气排放co2的碳排放强度；为t时刻能源站n的燃气消耗量；e
grid
为与大电网的购电排放co2的碳排放强度；η
grid
为电网传输效率；为t时刻能源站n与大电网的购电功率。
[0116]
综上所述，运用改进p-中位模型中求解输电管网的最短距离就是能量站沿着地面道路输送能量至用户负荷的最短距离。同理，能量站之间铺设的输电管网的长度也就是沿着地面道路相互传输能量的最短距离。本文将通过改进枚举法来对区域内的最短距离进行求解。改进枚举法的基本原理：在区域内，从用户负荷节点出发，考虑传输距离递增顺序，选择权重较小的能量站，循环逐渐得到最短路径为其传输能量。
[0117]
在区域综合能量站网络g＝(v，e，w)中，其中v＝m∪n∪q，m为用户负荷节点集合，n为能量站待选地址节点集合，q为路网节点集合。假设ψ(n)表示集合n的幂集，表示幂集ψ(n)中所有含k个元素的子集组成的集合。令表示中第o个元素，有z表示目标函数值，p表示中位点集合，x＝{xo|o＝1,2
…
}表示能量站供给用户负荷的分配情况，即x1表示第一个能量站供给的用户负荷的集合。令k＝1；z
→
∞；集合p，x和l均为空集。
[0118]
针对区域综合能量站网络g中每个顶点之间的相互连接的情形，根据下面计算方
法求解出边矩阵e。
[0119][0120]
式中：e(i,j)∈e i，j∈v
[0121]
已知区域综合能量站网络g中各节点位置信息及边矩阵e，根据下面计算方法求解出权重矩阵w。
[0122][0123]
式中w(i,j)为w的元素；i，j∈v；c
ep,ij
为输电管网造价模型；c
hp,ij
为供热管网造价费用模型；
[0124]
如图1所示，采用改进枚举法计算基于p-中位的选址模型，循环得到并输出优化函数值z，中位点集合p，用户负荷分配情况集合x；根据中位点集合p可以得到能量站的个数及地址，此时结合集合x及矩阵l，可计算出各用户负荷需求点到对应能量站的最优路径，其具体步骤如下：
[0125]
s1：设置最小权重矩阵d，计算相应的路径矩阵l。
[0126]
采用dijkstra算法求解区域综合能量站网络g各顶点间的最小权重，根据下面计算方法求解出最小权重矩阵d。
[0127][0128]
式中d
ij
为d的元素；i，j∈v；d
ij
为顶点i，j之间的的最小权重；记l(i,j)表示当顶点i和j取得最小权重时，二者之间的路径。记录取得最小权重时两顶点间的路径矩阵l，l为s
×
s阶矩阵，其中s＝|v|。
[0129]
s2：如果k》n0，转至s9；若否则进入s3；
[0130]
s3：令t＝1，计算
[0131]
s4：如果转至s2；若否则进入s5；
[0132]
s5：定义r为空集，对于给定m∈m,计算d
mo
,其中，记d
mn
＝min(d
mo
)，则将m记入集合r中，并令x(n)＝r；重复计算，直至m中的元素全部分配。
[0133]
s6：计算目标函数即
[0134][0135]
s7：如果令k＝k+1，转至s4；若否则进入s8；
[0136]
s8：令保存x，令k＝k+1，转至s4；
[0137]
s9：输出p、z、x；
[0138]
s10：获取能量站的数量、选址位置和管道路径。
[0139]
如图2所示，为南方某园区能量系统节点示意图。针对提出的基于改进p-中位的能量站选址优化模型，以南方某园区分为场景进行分析：该园区大致分为工业园、农业园、科技园、物流园四大区域，黑点代表用户负荷需求，白点代表园区适合建设能量站的位置。如图所示进行结点编号，共37个结点。为了满足用户负荷对需求电、热能源的需求，结合园区地质条件、气候条件和地面建筑等条件筛选出4个能量站的候选位置。
[0140]
模型中各用户负荷的电负荷、热负荷需求：d
hpi
＝500mm，c
ep,pipe,i
＝7 000元/m，c
es,n
＝10000元/kw，c
ep,linr,i
＝5 00元/m。根据第3部分模型求解方法,算例具体求解流程如下。
[0141]
1)构建边矩阵e和权重矩阵w。根据图2中各结点编号、结点直接关联情况，构建边矩阵e；如图2所示建立坐标系，根据坐标系获取各结点位置信息、边矩阵e，结合各结点坐标计算各相邻结点间的距离，计算各结点之间的权重，构建权重矩阵w。
[0142]
2)构建最小权重矩阵d和最短路径矩阵l。采用dijkstra最短路径求解算法，根据边矩阵e和权重矩阵w的求解结果，计算各结点之间的最小权重，构建最小权重矩阵d；在计算过程中，记录结点之间实现权重最小时经过的路径，构建最短路径矩阵l。各候选能量站(编号1、9、16、31)与各用户负荷(编号4、5、7、8、10至12、14、17、19、21、22、24、25、28、30、32)之间的最小权重，即候选能量站到相应用户负荷建设能量传输管网的最小投资费用。
[0143]
3)能量站与管网路径选择。第3节步骤7输出的数据结果中，根据集合p可以确定能量站的个数和位置，根据集合x可以确定每个能量站服务的用户负荷；参照最短路径矩阵l，可以确定任意能量站到对应用户负荷的最佳路径。
[0144]
如图3所示，为选址后的能量站选址和传输路径示意图。可以看出算例园区的能量站与管网路径的最佳布局，根据优化结果显示，4个候选能量站有3个被选中，每个能量站都对应一定的供能范围。其中4号、5号、8号、10号、14号和19号用户负荷由9号能量站供能，7号、11号、12号、17号、21号、22号和28号用户负荷由16号能量站供能，24号、25号、30号和32号用户负荷由31号能量站供能。实线路径则表示能量站到对应用户负荷的管网路径。
[0145]
以上详细描述了本发明的较佳具体实施例。应当理解，本领域的普通技术人员无需创造性劳动就可以根据本发明的构思作出诸多修改和变化。因此，凡本技术领域中技术人员依本发明的构思在现有技术的基础上通过逻辑分析、推理或者有限的实验可以得到的技术方案，皆应在由权利要求书所确定的保护范围内。