一种基于深度学习的高鲁棒性波前斜率预测方法

algorithmbased on lstm recurrentneural network.optik.220(16),4869-4880(2020).)。但是无论是波前数据还是电压数据，都存在维数较大的问题，会增加网络运行负担，并且预测过程中易引入较大误差，不利于后期校正。而对维度较小的波前斜率特征进行预测会大大提升网络效率，减小推理时间，并且斜率数据更加方便直接从传统ao系统中获取，可便于后期基于直接斜率法的波前校正。
5.因此，本发明提出一种基于深度学习的高鲁棒性波前斜率预测方法。


技术实现要素：

6.本发明解决的技术问题是：在校正具有高时间频率的大气湍流畸变波前的情况下，克服由于ao系统固有的时延误差而造成的变形镜补偿波前与实际畸变波前错位的问题。
7.本发明的技术方案是：一种基于深度学习的高鲁棒性波前斜率预测方法，其特征通过以下步骤实现：
8.步骤s1：根据大气冻结流假设，基于kolmogorov湍流统计理论、hv-57折射率结构常数模型和buffton风速模型经过傅里叶级数方法时间演化生成仿真数据，模拟获得大气湍流畸变波前；
9.步骤s2：对步骤1中收集的畸变波前数据进行预处理，采用哈特曼波前传感器仿真求解波前斜率，将所得斜率数据分为样本集与标签集两组数据；
10.步骤s3：配置深度学习环境，搭建基于convlstm网络的残差学习预测模型；
11.步骤s4：任意抽取样本集与标签集中80％的数据作为训练集，训练集中的数据须满足样本与标签相对应，供网络学习历史波前斜率与预测波前斜率的映射关系，从数据集剩下的 20％做为测试集，用于验证算法有效性；
12.步骤s5：利用测试集中样本波前数据进行模型测试，对输出预测波前斜率与实际标签波前斜率进行波前复原，并对复原波前残差进行对比分析，选取最优模型结构；
13.进一步地，所述步骤s1中kolmogorov湍流统计理论即为在惯性区域内大气折射率结构函数满足“三分之二定律”。
14.进一步地，所述步骤s3中利用spyder软件进行基于模型搭建。
15.进一步地，所述步骤s5中残差分析的评价指标为复原波前残差的均方根(rms)值。
16.本发明原理在于：本发明提供一种基于深度学习的高鲁棒性波前斜率预测方法，采用残差学习的方式消除相邻两帧之间的冗余信息，利用convlstm较强的记忆能力对精化融合后的特征进行多帧预测，最后，实现高鲁棒性的畸变波前斜率预测。
17.本发明与现有技术相比有如下优点：传统ao技术由于系统本身的校正时延误差，导致对高时间频率的大气湍流畸变波前校正效果不理想。对于现有未来多帧预测的神经网络类方法，基于简单网络模型的需要多帧先验波前帧数但预测效果鲁棒性却较低，基于较为复杂的网络模型可减少先验波前的数量，却同时带来了预测精度不够和预测效果鲁棒性低的问题，本发明采用残差学习的方式消除相邻两帧之间的冗余信息，利用convlstm较强的记忆能力对精化融合后的特征进行多帧畸变波前斜率预测，可有效避免ao系统固有的时延误问题带来的校正误差，且满足多帧未来波前的高鲁棒性预测性能。有望用于大气传输系统及更多相关领域的高时间频率波前畸变的预测校正。
附图说明
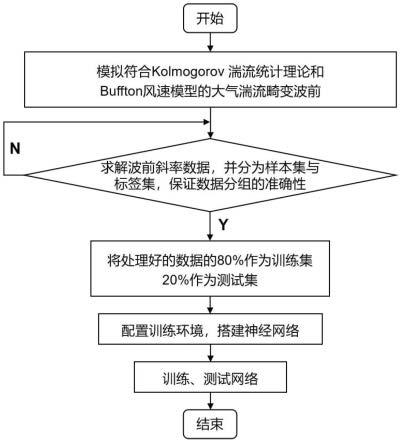
18.图1为本发明一种基于深度学习的高鲁棒性波前斜率预测方法工作流程图；
19.图2为本发明中基于convlstm网络的波前斜率预测模型；
20.图3为预测模型中的convlstm网络结构图。
具体实施方式
21.为使本发明的技术方案和优点更加清楚明白，以下结合具体实施例子，参照附图对本发明进一步详细说明。
22.图1是一种基于深度学习的高鲁棒性波前斜率预测方法工作流程图，具体步骤为：
23.步骤s1：根据大气冻结流假设，基于kolmogorov湍流统计理论、hv-57折射率结构常数模型和buffton风速模型经过傅里叶级数方法时间演化生成仿真数据，模拟获得大气湍流畸变波前；
24.步骤s2：对步骤1中收集的畸变波前数据进行预处理，采用哈特曼波前传感器仿真求解波前斜率，将所得斜率数据分为样本集与标签集两组数据；
25.步骤s3：配置深度学习环境，搭建基于convlstm网络的残差学习预测模型；
26.步骤s4：任意抽取样本集与标签集中80％的数据作为训练集，训练集中的数据须满足样本与标签相对应，供网络学习历史波前斜率与预测波前斜率的映射关系，从数据集剩下的 20％做为测试集，用于验证算法有效性；
27.步骤s5：利用测试集中样本波前数据进行模型测试，对输出预测波前斜率与实际标签波前斜率进行波前复原，并对复原波前残差进行对比分析，选取最优模型结构；
28.步骤s1中kolmogorov湍流统计理论即为在惯性区域内大气折射率结构函数满足“三分之二定律”。
29.折射率结构函数dn(r)满足“三分之二定律”可表示为：
[0030][0031]
其中，r为标量距离，为海拔高度h处的折射率结构常数，常用hv-57模型表示：
[0032][0033]
其中，一般取：v＝21m/s，a＝1.7
×
10-14
。
[0034]
但是在激光大气传输和自适应光学校正技术中，广泛采用大气相干长度r0来描述湍流效应的影响，并评价激光传输及其相位校正的效果。r0值越大，表示大气条件越好，一般情况下，r0和的关系为：
[0035][0036]
其中，k为波数，l为传输距离，为天顶角。
[0037]
当激光大气水平传输时，即r0表示为：
[0038]
[0039]
buffton风速模型表述为大气中风速随海拔高度的变化：
[0040][0041]
其中，一般取vg＝5m/s，v
t
＝30m/s，h
pk
＝9400，h
scale
＝4800。
[0042]
步骤s3中搭建的基于convlstm网络的预测模型采用残差学习的方式消除相邻两帧之间的冗余信息，然后将精化后的特征进行融合，过程如下所示：
[0043]fi
＝σ(ω1*concat(fi,f
i+1
)+k1)+fi[0044]
其中，σ表示激活函数，即prelu函数，concat表示连接操作，ω1和k1分别为一个1
ꢀ×
1卷积层的权值和偏差，“*”表示卷积操作，fi，f
i+1
为相邻两帧的畸变波前斜率矩阵， fi为两帧精化融合后的波前斜率特征。
[0045]
最后，把融合后的特征输入convlstm网络得到最终预测结果。其中convlstm主要包含一个记忆单元和三个控制门(输入门、输出门和忘记门)，其关键控制公式如下：
[0046]it
＝σ(w
ix
x
t
+w
ihht-1
+w
icct-1
+bi)
[0047]ft
＝σ(w
fx
x
t
+w
fhht-1
+w
fcct-1
+bf)
[0048]ot
＝σ(w
ox
x
t
+w
ohht-1
+w
occt-1
+bo)
[0049]ct
＝f
t
*c
t-1
+tanh(w
cx
x
t
+w
chht-1
+bc)
[0050]ht
＝o
t
*tanh(c
t
)
[0051]
其中，i
t
、f
t
、c
t
和o
t
分别表示输入门、忘记门、记忆单元和输出门。w
ix
、w
ih
和w
ic
是在最后时刻和记忆单元输出到输入门的权重矩阵。w
fx
、w
fh
和w
fc
是在最后时刻和记忆单元输出到忘记门的权重矩阵。w
ox
、w
oh
和w
oc
是在最后时刻和记忆单元输出到输出门的权重矩阵。 bi、bo、bf和bc分别为输入门、输出门、忘记门和记忆单元的偏置值。σ是s型类函数，tanh 是双曲切线函数。“*”表示卷积操作，h
t
为最后输出。
[0052]
预测过程如下：
[0053]
f1＝σ(ω2*concat(f1,f1)+b2)
[0054]
(c
t1
,h
t1
)＝convlstm_cell(f1,f1)
[0055]
f2＝σ(ω2*concat(f2,h
t1
)+b2)
[0056]
(c
t2
,h
t2
)＝convlstm_cell(f2,c
t1
)
[0057]
f3＝σ(ω2*concat(f3,h
t2
)+b2)
[0058]
(c
t3
,h
t3
)＝convlstm_cell(f3,c
t2
)
[0059]
p1＝σ(ω3*h
t1
+b3)
[0060]
p2＝σ(ω3*h
t2
+b3)
[0061]
p3＝σ(ω3*h
t3
+b3)
[0062]
其中，σ表示激活函数，即prelu函数，concat表示连接操作，(ω2,b2)和(ω3,b3)分别为1
×
1卷积层的权值和偏差，“*”表示卷积操作，convlstm_cell为上述convlstm网络的关键控制过程，最终的目标预测值为p1、p2和p3。
[0063]
本发明并不局限于上述的具体实施方式，上述的实施方式仅仅是示意性的，而不是限制性的。本领域的普通技术人员在本发明的启示下，在不脱离本发明宗旨和权利要求所保护的范围情况下，还可做出很多形式，这些均属于本发明的保护之内。本发明未详细阐
述部分属于本领域技术人员的公知技术。