基于DDQN-KRR的电气热协同的配电网动态重构方法及系统

基于ddqn-krr的电气热协同的配电网动态重构方法及系统
技术领域
1.本发明属于配电网重构相关技术领域，尤其涉及基于ddqn-krr的电气热协同的配电网动态重构方法及系统。


背景技术：

2.本部分的陈述仅仅是提供了与本发明相关的背景技术信息，不必然构成在先技术。
3.单一能源形式的配电网已难以满足经济性和碳排放的要求。考虑电-气-热多能流协同的配电网重构(distributionnetwork reconfiguration,dnr)成为提高配电系统经济效益和消纳新能源的重要手段。随着机器学习理论的发展，基于数据驱动的配电网动态重构一定程度上解决了动态重构难以满足系统对时效性和经济性要求的问题。因此，基于数据驱动并考虑综合能源(integrated energy system,ies) 的配电网动态重构成为研究的热点。关于dnr的研究已较为完善，dnr可分静态重构与动态重构。静态重构虽然计算效率高，但未考虑不同时段的源荷变化，难以得到理想的重构策略；动态重构因需考虑时段划分，计算时间相对较长，得到的重构策略往往不具有时效性。
4.文献“杨明,翟鹤峰,马嘉翼等.计及分布式电源发电不平衡度约束的三相不对称配电网动态重构[j].中国电机工程学报,2019,39(12): 3486-3499”提出一种计及分布式电源(distributed generation,dg)三相不对称的配电网动态重构方法，提高了三相不平衡网络的安全性与经济性。文献“翟鹤峰,杨明,赵利刚,等.提升分布式电源接纳能力的配电网三相鲁棒动态重构[j].电力系统自动化.2019,43(18):35-42.”基于二阶段鲁棒优化方法，利用配电网动态重构提高不可控分布式电源的并网能力。文献“易海川,张彼德,王海颖,等.提高dg接纳能力的配电网动态重构方法[j].电网技术,2016,40(05):1431-1436.”针对dg大量接入配电系统的问题，提出一种以提高dg接纳能力为目标的配电网动态重构方法，减少了舍弃dg的风险。“李扬，韦钢,马钰,等.含电动汽车和分布式电源的主动配电网动态重构[j].电力系统自动化.2018,42(05): 102-110.”提出一种基于区间数方法的含电动汽车和分布式电源的动态重构策略，实现了考虑多种不确定因素下主动配电网的动态重构。近年来，新兴算法的出现使得动态重构得到重构解的时间大大降低。文献“malekshah s,rasouli a,malekshah y,et al.reliability-drivendistribution power network dynamic reconfiguration in presence ofdistributed generation by the deep reinforcement learning method[j]. alexandria engineering journal,2022,61(8):6541-6556.”提出了一种基于动态重构方法，通过强化学习算法提高配电网在分布式发电情况下的可靠性。文献“ji x,yin z,zhang y,et al.real-time autonomousdynamic reconfiguration based on deep learning algorithm fordistribution network[j].electric power systems research,2021, 195(03):107132.”构建了基于长短期记忆神经网络(long short-termmemory,lstm)的配电网实时自主动态重构模型，降低了配电网功率损耗和开关动作成本。文献“bui v,su w.real-time operation of distribution
network:a deep reinforcement learning-based reconfigurationapproach[j].sustainable energy technologies and assessments, 2022,50(01):101841.”提出了一种动态网络重构策略，基于三阶段深度确定性策略梯度算法(deep deterministic policy gradient,ddpg)实现快速重构进而提高了配电网的稳定性和可靠性。上述文献均有效促进了配电网动态重构领域的发展，但未考虑ies对配电网动态重构的影响。
[0005]
综合考虑电-气-热ies与传统配电系统的深度融合，深度挖掘ies系统在能量传输和转化过程中的灵活性资源，可有效提高配电网动态重构的有效性。文献“靳小龙,穆云飞,贾宏杰,等.考虑配电网重构的区域综合能源系统最优混合潮流计算[j].电力系统自动化,2017,41(01): 18-24+56.”提出了计及配电网重构的电-气区域综合能源系统(integratedcommunity energysystem,ices)最优混合潮流算法，从“源-网-荷”多方面对ices进行调度优化，降低了ices成本。文献“陈泽兴,张勇军,黄豫,等.基于条件风险价值的综合能源配电网优化重构方法研究[j].全球能源互联网,2020,3(06):590-599.”建立了考虑配电网重构的电-气 ies优化运行模型，利用条件风险价值理论量化ies不确定性带来的运行风险，提升了ies的运行能力，并使配电网重构结果更具鲁棒性。文献“周步祥,姚先禹,臧天磊.计及电-气双向耦合的综合能源配电网优化重构 [j/ol].电测与仪表,2021[2022-10-05].”引入电转气装置，构建了计及配电网重构的电-气双向耦合ies模型，验证了配电网重构能够降低ies的运行费用，并可提高配电系统的运行电压水平和配气网的气压。文献“李鹏,王子轩,侯磊,等.基于重复博弈的区域综合能源系统优化运行分析 [j].电力系统自动化,2019,43(14):81-89.”提出了基于重复博弈的电
ꢀ‑
气区域ies优化方法，将配电网重构作为优化手段之一，有效降低了系统运行成本。上述研究虽然将ies与配电网重构综合考虑，但鲜有研究同时计及电网、热网和气网的协同运行；且现有研究多针对单一时间断面的静态重构，未考虑连续时间尺度的动态重构。


技术实现要素：

[0006]
为克服上述现有技术的不足，本发明提供了一种基于ddqn-krr的电气热协同的配电网动态重构方法及系统，
[0007]
为实现上述目的，本发明的一个或多个实施例提供了如下技术方案：基于ddqn-krr的电气热协同的配电网动态重构方法，包括：
[0008]
以配电网运行成本和配气网气源成本之和最小为优化目标函数，以配电网约束、配气网约束、配热网约束以及电-气-热耦合约束为约束条件，构建配电网动态重构模型；
[0009]
利用ddqn-krr对配电网动态重构模型进行求解，其中，基于节点负荷与dg出力通过krr模型预测耦合机组出力；基于节点负荷、dg出力以及所述耦合机组出力数据通过ddqn模型得到重构策略。
[0010]
本发明的第二个方向提供基于ddqn-krr的电气热协同的配电网动态重构系统，包括：
[0011]
模型建立模块：以配电网运行成本和配气网气源成本之和最小为优化目标函数，以配电网约束、配气网约束、配热网约束以及电-气-热耦合约束为约束条件，构建配电网动态重构模型；
[0012]
模型求解模块：利用ddqn-krr对配电网动态重构模型进行求解，其中，基于节点负
荷与dg出力通过krr模型预测耦合机组出力；基于节点负荷、 dg出力以及所述耦合机组出力数据通过ddqn模型得到重构策略。
[0013]
以上一个或多个技术方案存在以下有益效果：
[0014]
(1)提出了电-气-热协同的配电网动态重构模型，基于系统历史状态连续数据集，通过静态重构压缩dnr的解空间，并建立与配网状态一一对应的数据库，在此过程中依据时间序列考虑开关动作成本，进而制定出动态重构策略。
[0015]
(2)提出了基于ddqn的动态重构模型，将传统动态重构模型耗时较多的潮流计算转移到模型训练过程中，深度挖掘数据库中配电网运行状态与重构策略之间的映射关系，模型训练完成后可直接根据系统当前状态快速得到重构策略。
[0016]
(3)提出了基于krr的耦合机组出力预测方法，探索节点负荷、dg出力与耦合机组出力之间的映射规律，能够较为准确地推演不同数据集之间的非线性函数关系，从而实现了在线应用过程中实时获取耦合机组的最优出力。
[0017]
本发明附加方面的优点将在下面的描述中部分给出，部分将从下面的描述中变得明显，或通过本发明的实践了解到。
附图说明
[0018]
构成本发明的一部分的说明书附图用来提供对本发明的进一步理解，本发明的示意性实施例及其说明用于解释本发明，并不构成对本发明的不当限定。
[0019]
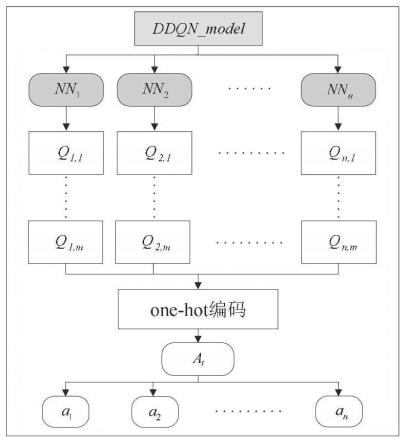
图1为本发明实施例一中ddqn模型改进及编码方式示意图；
[0020]
图2为本发明实施例一中模型训练及应用过程示意图；
[0021]
图3为本发明实施例一中krr预测结果示意图；
[0022]
图4为本发明实施例一中静态重构后解空间变化；
[0023]
图5为本发明实施例一中四种场景线总成本及电压对比示意图；
[0024]
图6为本发明实施例一中不同发电设备出力示意图；
[0025]
图7是本发明实施例一中e33-g20-h16系统图。
具体实施方式
[0026]
应该指出，以下详细说明都是示例性的，旨在对本发明提供进一步的说明。除非另有指明，本文使用的所有技术和科学术语具有与本发明所属技术领域的普通技术人员通常理解的相同含义。
[0027]
需要注意的是，这里所使用的术语仅是为了描述具体实施方式，而非意图限制根据本发明的示例性实施方式。
[0028]
在不冲突的情况下，本发明中的实施例及实施例中的特征可以相互组合。
[0029]
实施例一
[0030]
本实施例公开了基于ddqn-krr的电气热协同的配电网动态重构方法，首先，建立包含电-气-热协同的配电网状态与其静态重构结果的数据库，依据时间序列考虑开关动作成本，制定出动态重构策略；其次，提出内核岭回归方法，用于预测耦合机组的最优出力；最后，基于双层深度q网络挖掘配电网状态与重构结果之间的映射关系，实现快速动态重构。
[0031]
在本实施例中，基于ddqn-krr的电气热协同的配电网动态重构方法具体包括：
[0032]
步骤1：以配电网运行成本和配气网气源成本之和最小为优化目标函数，以配电网约束、配气网约束、配热网约束以及电-气-热耦合约束为约束条件，构建配电网动态重构模型；
[0033]
步骤2：利用ddqn-krr对配电网动态重构模型进行求解，其中，基于节点负荷与dg出力通过krr模型预测耦合机组出力；基于节点负荷、dg出力以及所述耦合机组出力数据通过ddqn模型得到重构策略。
[0034]
在本实施例步骤1中，以配电网线损成本、开关动作成本、变电站购电成本以及天然气网气源成本之和最小为优化目标。为了提高新能源发电设备利用率，本实施例不考虑其成本；由于耦合机组都以天然气作为燃料，本实施例将两者燃料成本都计入气源成本中。目标函数为：
[0035][0036]
式中，和分别为t时段配电网运行成本和配气网气源成本；c
l
、 c
sub
、cd和c
gas
分别为配电网线损、配电网购电、配电网开关动作和气源出力成本系数；b、ω、k和s分别为配电网支路集合、配电网节点集合、配气网集合和气源集合；δ
b,t
和为0-1变量，当δ
b,t
＝1/0时分别表示t时段支路b的开关从断开到闭合和开关无动作；当时分别表示t时段支路 b的开关从闭合到断开和开关无动作；为t时段配电网第b条支路的电流；为t时段与节点i相连的变电站有功出力；rb为配电网第b条支路的电阻；为t时段第k个气网中第s个气源出力。
[0037]
约束条件包括配电网约束、配气网约束、配热网约束以及电-气-热耦合约束。
[0038]
具体的，1、配电网约束包括：配电网潮流约束；系统安全约束；网络辐射状约束。
[0039][0040][0041][0042][0043]
式中，b(i,j)为首节点为i末节点为j的支路b；p
b,t
和q
b,t
分别为t时段流经支路b的有功与无功功率；和分别为t时段节点i的注入有功与无功功率；为t时段与节点i相连的变电站无功出力；和分别为 t时段与节点i相连的dg有功与无功出力；和分别为t时段与节点 i相连的chp有功与无功电出力；和分别为t时段与节点i
相连的 gt有功与无功出力；和分别为t时段与节点i相连的有功和无功负荷。
[0044][0045][0046][0047]
式中，u
i,t
为t时段节点i的电压；和分别为节点i的最低和最高允许电压；γ
b,t
为0-1变量，γ
b,t
＝1/0分别表示t时段支路b连通和断开；为支路b的最大允许电流；p
idg,max
、p
igt,max
和p
ichp,max
分别为与节点i相连的dg、 gt和chp有功功率最大值；θ
dg
、θ
gt
和θ
chp
分别为dg、gt与chp的功率因数角。
[0048][0049]
μ(i,j)+μ(j,i)＝γ
b,t
(10)
[0050][0051][0052][0053]
式中，a为系统节点总数；μ为节点父子关联矩阵，μ(i,j)＝1表示节点i 为节点j的父节点；a(l
τ
(j))为0-1变量，a(l
τ
(j))＝1/0分别表示环路τ第j个开关连通和断开。
[0054]
2、天然气网约束包括：流量约束；管道流量约束；气源出力约束；节点压力约束。本实施例涉及的天然气网为覆盖范围较小的配气网，因此不需要考虑加压站。
[0055][0056]
式中，为t时段与节点m相连的气负荷；和分别为t时段 chp机组c和gt机组g的耗气量。
[0057][0058][0059]
式中，g
k,mn,t
为t时段节点mn之间的管道流量；p
k,m,t
和p
k,n,t
分别为t时段节点m和n
的压力；j
k,mn
为节点mn之间管道的参数，与管道直径等有关；和分别为管道mn流量的最小值与最大值。
[0060][0061]
式中，和气源出力的最小值与最大值。
[0062][0063]
式中，和分别为节点压力最小值与最大值。
[0064]
3、热网约束包括：热功率平衡约束；chp和换热站(heat exchangestation,hes)温度约束；热网温度约束。
[0065][0066]
式中，π
chp
和π
hes
分别为chp和hes集合；为t时段chp机组c的热功率；为t时段第h个hes的热功率；和分别为t时段chp 机组c的去水管和回水管温度；和分别为t时段第h个hes的去水管和回水管温度；和分别为t时段chp机组c和第h个hes的水流量；为水的比热容。
[0067][0068]
式中，和分别为chp机组c去水温度最小值和最大值；和分别为第h个hes回水温度最小值和最大值。
[0069][0070]
式中，π
p-和π
p+
分别为以o为终点和起点的管道集合；m
k,l,t
为t时段管道l的水流量；和分别为t时段去水管道l的出口和入口温度；和分别为t时段回水管道l的出口与入口温度；和分别为t时段去水管和回水管上节点o的混合温度。
[0071]
4、电-气-热耦合约束包括：chp机组电-气-热耦合约束；gt机组电
‑ꢀ
气耦合约束。
[0072][0073]
[0074]
式中，与分别为chp机组c与gt机组g的转换效率；q
gv
为天然气高热值。
[0075]
在本实施例中，对于配电网潮流约束中存在的非线性方程不易求解的问题，通过big-m与二阶锥方法对其进行线性化处理。为了简化配电网重构的流程，利用配电网“闭环建设，开环运行”的特点，将一个联络开关与多个分段开关编为基本环路矩阵(basic loop matrix,blm)，通过静态重构压缩blm，并记压缩后的矩阵为blm*。
[0076]
针对原始潮流中存在非线性方程不易求解的问题，引入变量和通过big-m方法，将式转化为线性形式：
[0077][0078]
式中，m为一个较大的整数。
[0079]
通过二阶锥方法将式中的二次等式松弛为标准二阶锥形式：
[0080][0081]
式中，||
·
||2表示2范数。
[0082]
利用配电网“闭环建设，开环运行”的特点，将配电网中一个联络开关与多个分段开关视为一个基本环路，并将多个基本环路包含的开关编号按行排列组成基本环路矩阵(basic loop matrix,blm)，重构时按照基本环路进行编码，只需从blm的每一行中选取一个开关断开即完成一次重构。在blm中，存在一定数量致使系统运行成本较高的开关组合，通过静态重构可以筛选出这些开关组合，即剔除blm中的劣质重构解，进而压缩dnr 的解空间，将压缩后的矩阵记为blm*。
[0083]
针对天然气网中管道流量约束存在二次函数表达，本实施例采用增量分段线性化方法对其进行处理，具体为：
[0084][0085]
式中，ω
ω
为0-1变量，表示第ω个分段区间上的位置；φm为0-1变量。
[0086]
令和并引入辅助变量和则由式(15) 可转化为：
[0087][0088]
式中，为区间变量；n为分段区间数量；为0-1变量。
[0089]
ddqn模型由qpre和qtar这两个结构相同的神经网络组成，qpre依据当前配电网状态得到开关动作，并在每次训练完成后更新网络参数；qtar 用于计算目标q值，并在训练规定次数之后将qpre的网络参数复制到qtar 中。这种异步网络更新的方式通过将开关动作的选择和目标q值的计算解耦，解决了原始深度q网络(deep q network,dqn)中的过估计问题。在上述训练过程中，ddqn模型不断访问配电网状态和开关动作等数据，因此需要一个能够承载此类信息的数据库以供模型使用，此数据库包括描述配电网状态的st、开关动作组合at及回报值rt等参数。
[0090]
假设从数据库中选取t时段的数据作为当前状态，以t+1时段的状态 st+1和动作at+1计算当前q值，并依据贪婪原则选择当前动作：
[0091][0092]
式中，θ
t
为qpre的网络参数；χ为0到1之间的随机数；ε为贪婪概率，且ε∈[0,1]。可见，q网络有一定概率选择一个随机动作，这样可以增加搜索动作的多样性，使模型避免陷入局部最优。
[0093]
根据当前动作a(s
t+1
；θ
t
)计算当前目标q值：
[0094][0095]
式中，γ为衰减因子且γ∈[0,1]；为qtar的网络参数。
[0096]
然后使用q
pre
(s
t
,a
t
；θ
t
)和计算loss值：
[0097][0098]
式中，m为训练时批量采样的数量。
[0099]
对于krr算法，krr将核方法引入岭回归中，使其能够建立配电网状态与耦合机组出力之间的非线性关系，进而处理此类非线性问题[19]。
[0100]
设线性模型为：
[0101]
g(c)＝c
t
x
ꢀꢀ
(31)
[0102]
式中，c
t
＝(c1,c2...cn)为参数矩阵；t为矩阵转置；x＝(x1,x2…
xn)为配电网状态矩阵，包括节点负荷与dg出力。
[0103]
定义g＝(g1,g2,
…
,gn)为耦合机组出力矩阵，则损失函数为：
[0104]
[0105]
设模型的估计值为：
[0106]
c1＝argminloss
krr
(c)
ꢀꢀꢀꢀꢀ
(33)
[0107]
为了解决因样本不足导致的矩阵不可逆问题，引入正则化方法：
[0108]
argmin[loss
krr
(c)+υp(c)]
ꢀꢀꢀꢀꢀꢀ
(34)
[0109]
式中，υ为超参数矩阵；p(c)为正则化函数。
[0110]
联立上式，解得其估计值：
[0111]
c1＝(x
t
x+υ-1
e)-1
x
tgꢀꢀꢀꢀ
(35)
[0112]
式中，估计值c1为半正定矩阵与对角矩阵之和，故c1正定并且可逆； e为单位矩阵。
[0113]
引入内核空间，将参数矩阵c1的最优解转化为内积形式，根据矩阵求逆引理化简可得：
[0114][0115]
式中，ξ为权重参数矩阵。
[0116]
在本实施例步骤2中，基于上述可知，ddqn模型依据数据库中的st、 at及rt计算并最大化q值完成训练和寻优过程，然而此时模型只能单维输出，为了满足重构模型单次输出一个包含多个基本回路开关状态的要求，需要增加ddqn的输出维数。
[0117]
其中，如图1所示，对于ddqn模型的改进为：在ddqn模型输出之后加入与blm中元素一一对应的全连接神经网络，实现ddqn模型的多维输出；引入one-hot原则对模型输出结果进行编码，保证每个基本环路仅断开一个开关。
[0118]
在本实施例中，ddqn模型数据库的建立过程如下：
[0119]
1)静态重构。基于计及电-气-热协同的配电网静态重构模型使用节点负荷与dg出力等历史信息进行静态重构，进而获得配电网重构解与耦合机组出力等数据。静态重构模型不考虑配电网的开关动作成本，其余部分与动态重构模型相同，因此其目标函数为：
[0120][0121]
2)建立数据库。将配电网状态、开关动作及回报值等储存至数据库中。回报值通过式(38)计算。
[0122]
其中，回报值rt是更新q值与计算q值的基础，因此在配电网重构问题中，r
t
可设置为目标函数的倒数，即：
[0123][0124]
式中，c
t
为重构模型的目标函数。
[0125]
如图2所示，计及电-气-热多能协同的配电网动态重构模型采用“离线训练，在线应用”的方法获得重构策略。
[0126]
离线训练步骤如下：
[0127]
1)生成数据库。基于历史dnr数据和配电网结构参数通过静态重构生成数据库。
[0128]
2)训练krr模型。通过式计算并更新模型参数，将训练完成后模型保存，以便在线应用时使用。
[0129]
3)初始化训练状态。将模型输入状态、动作和回报等变量清空，为训练模型做准备。
[0130]
4)计算q
pre
值并决策动作。随机选取数据库中h个数据，通过式计算 qpre值并依据贪婪原则决策动作。
[0131]
5)计算q
tar
值。根据步骤4)中得到的动作，并由式计算q
tar
值。
[0132]
6)计算loss值并更新q
pre
网络。将得到的q
pre
与q
tar
值代入式，计算loss值，采用随机梯度下降法更新q
pre
网络参数。
[0133]
7)判断并更新q
tar
网络。判断是否达到规定训练次数e，达到则将此时qpre的网络参数复制到q
tar
中，反之则不复制。
[0134]
8)输出模型。当达到最大训练次数后，保存ddqn模型至在线应用时使用，否则返回步骤3)。
[0135]
在线应用步骤如下：
[0136]
1)预测耦合机组出力。基于节点负荷与dg出力通过krr模型预测耦合机组出力。
[0137]
2)获得动态重构策略。基于节点负荷、dg出力以及步骤1)中耦合机组出力数据通过ddqn模型快速得到重构策略。
[0138]
本实施例以33节点配电网、20节点配气网及16节点配热网 (e33-g20-h16)和e78-g40-h32系统为例，验证所提模型的有效性。使用 matlab调用cplex求解器进行静态重构以建立数据库；使用pycharm软件训练ddqn模型，设置衰减因子为0.99，学习率为0.001，数据库容量为 50000，训练轮数为5000，批处理数为128，贪婪概率为0.8；使用jupyternotebook软件训练krr模型，核函数为sigmoid，学习率为0.001。仿真使用的计算机系统为win10；cpu为intel core i5-11300h，基准主频为 3.10ghz；内存为16gb。
[0139]
e33-g20-h16算例系统结构图如图7所示。仿真模型中配电网参数设置参考文献[16]，配气网与配热网参数设置参考文献“陈曦.计及网络动态特性的综合能源系统优化调度方法研究[d].济南:山东大学,2020.”。配电网负荷与dg出力来自文献“zhang l,wang g,giannakis g b.real-timepower system state estimation and forecasting via deep unrolledneural networks[j].ieee transactions on signal processing.2019, 67(15):4069-4077.”，气负荷与热负荷数据来自文献“张玉敏,张旋,吉兴全,等.计及电-气-热ies动态特性的输配协同机组组合[j/ol].中国电机工程学报,2022[2022-10-05].”。电网中有4个dg，光伏与风电设备各2台，其数据如表c1所示；气网中设置2台gt实现电-气耦合；热网中设置2台chp实现电-气-热耦合；耦合机组的数据如表c2所示。
[0140]
表c1e33-g20-h16分布式电源数据
[0141][0142]
表c2e33-g20-h16耦合机组数据
[0143][0144]
为了解决在线应用时耦合设备gt和chp机组出力不易获取的问题，提出能够有效处理非线性问题的krr方法预测耦合机组出力。为了模拟现实情况中存在的量测误差，引入均值为0，协方差为10-3i和10-7i，权重为 0.65和0.35的双峰高斯噪声。各耦合机组的预测结果如图3所示，其中真实值是由静态重构获得的耦合机组出力数据。
[0145]
由图3可知，预测值与真实值曲线相差不大。即使节点负荷、dg出力与耦合机组gt、chp出力之间存在复杂的非线性映射关系，krr模型依然能够精准地预测出耦合设备gt与chp机组的出力。原因在于，本实施例所提 krr采用了核方法，将低维数据推至高维，并在高维空间进行非线性拟合，使其具备了强大的解决非线性问题的能力。
[0146]
为了减少ddqn-krr算法的寻优范围，本实施例通过静态重构剔除原始 blm中的劣质解，达到压缩dnr解空间的目的。blm与blm*分别如表1和图 4所示。
[0147]
表1ieee 33节点系统blm与blm*
[0148][0149][0150]
由表1和图4可知，环路ⅰ中解数量由9个缩减为4个；环路ⅱ中解数量由7个缩减为2个；环路ⅲ中解数量由14个缩减为3个；环路ⅳ中解数量由21个缩减为3个；环路
ⅴ
中解数量由10个缩减为4个。可见，静态重构可以剔除存在blm中致使系统运行成本较高、用户电压水平偏低的开关组合等劣质重构解，进而大大压缩了dnr的解空间，使ddqn-krr在更小的解空间中寻优，提高了模型求解的效率。
[0151]
为了分析ies系统对配电网重构的影响，本实施例设置以下四个场景：
[0152]
场景一：电网单独运行；
[0153]
场景二：电-气协同运行；
[0154]
场景三：电-热协同运行；
[0155]
场景四：电-气-热协同运行。
[0156]
四种场景的配电网线损、总运行成本以及最低节点电压分别如图5和表2所示。
[0157]
表2四种场景系统运行结果
[0158][0159]
由图5(a)可知，在24个时段内场景四的总运行成本是最低的，这表明电-气-热多能流协同作用可以赋予系统更高的灵活性，从而更好地平衡线损成本、购电成本及气源成本间的关系，达到降低运行总成本的目的。由图5(b)可知，计及电-气-热ies协同的配电网中最低节点电压得到了不同程度的提高。24h时段内，场景三的最低节点电压虽然都高于场景一，但 8h-22h时段内其最低节点电压仍低于0.95p.u.，不能满足用户对电压水平的要求；场景二与场景四的最低节点电压都高于0.95p.u.，并且场景四的电压均高于其他三个场景，这表明电-气-热多能流协同相较于电-气或电
‑ꢀ
热协同在提高节点电压水平方面更具有优势。
[0160]
由表2可知，考虑多能流耦合之后，gt与chp机组的并网缩短了电能运输距离使得配电网线损量大幅降低。场景一的运行成本最高为 9732.92usd，而考虑多能耦合的其他三个场景运行成本更低；场景二仅考虑电-气耦合，gt机组相较于chp机组具有更高的灵活性，可以根据配电网需求提供电功率，因此场景二的最低节点电压高于场景三；场景三仅考虑电-热耦合，但热负荷需求又使chp出力不为0，由于chp机组“以热定电、联合生产”的特性，这部分电能未并网而被“浪费”，最终导致场景二的成本高于场景三；场景四兼具场景二与场景三的优势，在总成本降低5.06％的同时将最低节点电压提高至0.9586p.u.。由此可见，电-气-热协同更能提高多种能源的耦合优势，在降低系统总运行成本的同时提高系统电压水平。
[0161]
为了验证ddqn-krr在dnr中的性能优势，将其分别与静态重构、文献“李超,苗世洪,盛万兴,等.考虑动态网络重构的主动配电网优化运行策略[j].电工技术学报,2019,34(18):3909-3919.”中misocp动态重构和文献“ji x,yin z,zhang y,et al.real-time autonomous dynamicreconfiguration based on deep learning algorithm for distributionnetwork[j].electric power systems research,2021,195(03):107132.”中lstm动态重构做比较，并将未重构网络作为对照组。其中，lstm动态重构中耦合机组出力也使用krr方法预测；未重构是指保持ieee33系统中联络开关s33，s34，s35，s36和s37始终处于断开状态。不同算法的系统运行结果如表3所示。
[0162]
表3四种场景系统运行结果
[0163]
[0164][0165]
由表3可知，未重构组仅依靠电-气-热多能协同来降低系统总运行成本，因此其耦合机组出力与变电站购电之比高达1.0152:1，使系统最低节点电压也能达到0.95p.u.，但拓扑结构的限制使得较高的耦合机组出力未能降低配电网的运行成本，最终导致未重构组总运行成本较高，这证明了将ies系统与dnr综合考虑的必要性。静态重构较好地平衡了耦合机组出力与变电站购电之间的平衡，但频繁的开关动作甚至使其运行总成本比未重构组高0.151％。misocp动态重构考虑了开关动作成本，其运行总成本低于静态重构，但因为耦合机组出力与变电站购电之比仅为0.4692:1，导致其线损量较大。lstm与ddqn-krr方法都依赖于krr获得耦合机组出力情况，因此两种方法的耦合机组出力与变电站购电之比与静态重构相近，而 ddqn-krr总运行成本低至9240usd，最低节点电压提升至0.9586p.u.，表明本实施例所提方法能更深度地挖掘历史数据的特征并决策出更优的重构策略，并提高配电网节点电压水平。
[0166]
为了验证ddqn-krr方法在计算效率方面的优势，将其与静态重构、 misocp动态重构和lstm动态重构对比，四种算法的对比结果如表4所示。
[0167]
表4四种算法的训练及运行时间
[0168][0169]
由表4可知，本实施例所提ddqn-krr方法获得重构策略的平均时间仅为0.0131s，均低于lstm方法的0.0657s、静态重构方法的3.23s和misocp 动态重构方法的342.64s。可见，本实施例所提ddqn-krr方法的计算效率最高。ddqn-krr与lstm方法都能实现毫秒级别的快速重构，但lstm方法对每一条基本环路建模，基本环路越多得到重构解的时间越长，而本实施例所提ddqn-krr方法将所有环路都揉合于一个模型中，可以直接得到整个系统的重构策略，大大减少了重构时间。
[0170]
电-气-热协同运行除了能够降低系统总运行成本以外，还可以一定程度上实现“削峰填谷”。系统中不同发电设备的出力情况如图6所示。
[0171]
由图6可知，在8-15h时段内dg的出力较高，而gt与chp的出力相对较低，表明电-气-热协同运行时，可在dg出力高峰时段减少耦合机组gt 与chp的出力进而减少用气量，这就等效地将电能转化为天然气并储存起来，为消纳dg出力提供了充足的空间。在2-7h时段内负荷较小，耦合机组主动减小出力促进电网对dg的消纳。16-24h时间段内，dg出力较低而 gt与chp出力较高，表明电-气-热协同运行，可在dg出力低谷时段将天然气和热能转化为电能以满足负荷需求。由此可得，ies协同能在一定程度上平抑dg并网带来的功率波动，起到“削峰填谷”的作用。
[0172]
e78-g40-h32算例：为了进一步验证所提ddqn-krr模型和方法的有效性和实用性，
以某市78节点配电系统、2个20节点配气以及4个8节点配热网构成的e78-g40-h32系统为例进行分析，e78参数如表c3所示。系统中共有8台dg，具体设置如表c4；4台gt以及4台chp，具体设置如表c5。
[0173]
表c3某市改进78节点配电系统网络参数
[0174]
[0175]
[0176][0177]
表c4 e78-g40-h32系统分布式发电设备数据
[0178][0179]
表c5 e78-g40-h32系统耦合机组数据
[0180][0181]
为了验证本实施例所提ddqn-krr方法在大规模配电系统中的依然具有优越的性能，将其与未重构、静态重构、misocp动态重构以及lstm动态重构等方法比较，其中未重构指s78，s79，s80，s81和s82始终处于断开状态。五种算法的运行结果如表5所示。
[0182]
表5五种算法的运行结果
[0183][0184]
由表5可知，未重构组因不能改变拓扑结构导致耦合机组出力与变电站购电之比以及线损量都较高，致使其运行总成本高达17428.20usd。静态重构因开关频繁动作导致总运行成本比未重构组高0.115％。misocp动态重构考虑了开关动作使其总成本下降了0.610％，因耦合机组出力与变电站购电之比较大导致线损量最少，这是因为考虑开关动作后系统优先增大耦合机组出力而非改变拓扑结构来降低总运行成本。lstm与ddqn-krr方法的耦合机组出力与变电站购电之比与静态重构基本相同，因此三种方法的线损量也相差不大，其中ddqn-krr方法总成本下降了0.756％，皆优于其他四种方法，这表明本实施例提出
的ddqn-krr方法在大规模ies系统中也有良好的适用性。所有方法最低节点电压都大于0.95p.u.，这是因为耦合机组的大量投运使得ies系统充分协同运行提高了节点电压均值。
[0185]
为了验证本实施例所提ddqn-krr方法在大规模配电系统中的计算效率优势，将其与静态重构、misocp动态重构和lstm动态重构对比，四种算法的对比结果如表6所示。
[0186]
表6四种算法的训练及运行时间
[0187][0188]
由表6可知，ddqn-krr算法计算效率的优势更加明显。静态重构与 misocp动态平均重构时间分别大幅度增加至7.44s和516.35s，而ddqn-krr 和lstm方法平均重构时间分别为0.0193s和0.0947s，仍能维持在毫秒级并实现快速重构。综上所述，ddqn-krr方法在大规模ies系统中依然具有良好的实用性。
[0189]
本实施例针对动态重构计算效率低的问题，提出了基于ddqn-krr的电
ꢀ‑
气-热ies协同的配电网动态重构模型。通过e33-g20-h16和e78-g40-h32 算例验证，得到：
[0190]
1)本实施例提出的krr方法能够准确地预测耦合设备gt与chp机组的出力，解决了在线应用时耦合机组出力不易获取的问题。
[0191]
2)计及电-气-热ies协同的dnr，系统能依据不同类型能源的特性，发挥其资源优势互补，可以在一定程度上平抑dg并网造成的功率波动，起到“削峰填谷”的作用，达到降低系统总运行成本以及提高用户电压水平的目的。
[0192]
3)相较于其他重构算法，本实施例提出的ddqn-krr算法兼顾重构策略的经济性和计算效率并实现了动态快速重构，且在大规模电-气-热ies 系统中有良好的适用性。
[0193]
实施例二
[0194]
本实施例的目的是提供基于ddqn-krr的电气热协同的配电网动态重构系统，包括：
[0195]
模型建立模块：以配电网运行成本和配气网气源成本之和最小为优化目标函数，以配电网约束、配气网约束、配热网约束以及电-气-热耦合约束为约束条件，构建配电网动态重构模型；
[0196]
模型求解模块：利用ddqn-krr对配电网动态重构模型进行求解，其中，基于节点负荷与dg出力通过krr模型预测耦合机组出力；基于节点负荷、 dg出力以及所述耦合机组出力数据通过ddqn模型得到重构策略。
[0197]
实施例三
[0198]
本实施例的目的是提供一种计算装置,包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序，所述处理器执行所述程序时实现上述方法的步骤。
[0199]
实施例四
[0200]
本实施例的目的是提供一种计算机可读存储介质。
[0201]
一种计算机可读存储介质，其上存储有计算机程序，该程序被处理器执行时执行上述方法的步骤。
[0202]
以上实施例二、三和四的装置中涉及的各步骤与方法实施例一相对应，具体实施方式可参见实施例一的相关说明部分。术语“计算机可读存储介质”应该理解为包括一个或多个指令集的单个介质或多个介质；还应当被理解为包括任何介质，所述任何介质能够存储、编码或承载用于由处理器执行的指令集并使处理器执行本发明中的任一方法。
[0203]
本领域技术人员应该明白，上述本发明的各模块或各步骤可以用通用的计算机装置来实现，可选地，它们可以用计算装置可执行的程序代码来实现，从而，可以将它们存储在存储装置中由计算装置来执行，或者将它们分别制作成各个集成电路模块，或者将它们中的多个模块或步骤制作成单个集成电路模块来实现。本发明不限制于任何特定的硬件和软件的结合。
[0204]
上述虽然结合附图对本发明的具体实施方式进行了描述，但并非对本发明保护范围的限制，所属领域技术人员应该明白，在本发明的技术方案的基础上，本领域技术人员不需要付出创造性劳动即可做出的各种修改或变形仍在本发明的保护范围以内。