一种结合卷积神经网络和卷积差分格式的流场计算方法

1.本发明属于流体力学领域，具体涉及一种结合卷积神经网络和卷积差分格式的流场计算方法。


背景技术：

2.在流体力学领域，通过传统数值方法求解流场的方式，已经表现出了非常优秀的性能。目前，存在一些众所周知的cfd软件，例如cfx、fluent等，通过使用这些软件，可以方便地对流场进行数值求解。但是，方便的同时，造成了一些不灵活，例如很难在这些商用软件的基础上进行自由的二次开发工作，核心技术已经被打包。随着人工智能技术的发展，出现了一类能够融合物理知识约束的神经网络，即内嵌物理知识神经网络，它依赖神经网络强大的表达能力，在求解偏微分方程这一类工作上，表现出较好的性能。在这一方法中，关于微分方程中各阶微分项的计算，完全依赖于自动微分技术，虽然神经网络自身有很强的非线性表达能力，但是由于其基本单元仍是线性单元，通过自动微分求解输出的各阶微分项，难以保证其微分项的非线性表达能力。在已有的一些工作和实际的试验中，已经发现这一问题的存在，例如在计算大雷诺数下的navier-stokes方程时，方程的解变得极不稳定，导致这一方法难以获得实际应用。
3.因此，有必要对上述方法进行改进，上述神经网络方法在计算微分项时，依赖于自动微分技术，而在传统数值求解方法中，各阶微分项依赖于网格节点之间的位置关系，即利用周围节点的参数值，差分计算该节点的参数微分值，即难以保证其微分项的非线性表达能力。


技术实现要素：

4.要解决的技术问题：
5.为了避免现有技术的不足之处，本发明提供一种结合卷积神经网络和卷积差分格式的流场计算方法，将传统数值方法中求解微分的差分方法与图像卷积计算、卷积神经网络相结合。本发明方法利用卷积神经网络的强大表达能力和基于网格构造稳定的卷积差分格式，得到更为精准的流场解，同时也能更为灵活、自由地进行求解设计。以至少解决现有内嵌物理知识神经网络在求解流场时的不稳定性问题，传统数值方法受限于商用cfd软件的问题。
6.本发明的技术方案是：一种结合卷积神经网络和卷积差分格式的流场计算方法，其特征在于具体步骤如下：
7.步骤一：确定流体物性参数以及边界条件；
8.步骤二：建立卷积核差分算子并划分流体域网格；
9.步骤三：建立卷积神经网络；
10.步骤四：初始化流场参数；
11.步骤五：计算神经网络损失函数值；
12.步骤六：训练神经网络直至收敛；
13.步骤七：计算流场云图；将需要计算的流场图输入步骤六中训练完成的卷积神经网络，得到的输出云图即为所求流场结果。
14.本发明的进一步技术方案是：所述步骤一中，需要确定的流体物性参数以及边界条件包括流体密度、流体粘性系数、流体初始压力、流体初始温度、流体初始速度分布、流体初始压力分布、固体换热边界条件、速度边界条件。
15.本发明的进一步技术方案是：所述步骤二中，对于一阶微分项，采用一维卷积算子进行差分计算，对于拉普拉斯算子，采用二维卷积算子进行差分计算，依据步骤一中的边界条件，选择合适的差分类型，针对不同差分类型设置不同大小的卷积核；流体域的划分需要与卷积核差分算子相匹配，对于规则流体域，采用直角坐标系直接划分流体域，对于不规则流体域，采用贴体坐标系划分网格。
16.本发明的进一步技术方案是：所述步骤三中，卷积神经网络采用编码器-解码器encoder-decoder框架，包括u型卷积神经网络u-net结构和全卷积神经网络fcn结构。
17.本发明的进一步技术方案是：所述步骤三中，神经网络的深度和各层节点数由步骤二中划分的计算流体域网格数直接决定，两者成正比关系。
18.本发明的进一步技术方案是：所述步骤三中，对于一个64
×
64的流体域，需要2层编码器encoder和2层解码器decoder，每层64个节点。
19.本发明的进一步技术方案是：所述步骤四中，初始化流场速度、压力、密度、温度目标参数，形成流场云图，将流场云图输入给步骤三中的卷积神经网络，经过编码器encoder提取高维特征，再经过解码器decoder复原到流场云图。
20.本发明的进一步技术方案是：所述步骤五中，神经网络的误差函数值由两部分加权组成，边界条件误差和控制方程误差；边界条件误差依据步骤一中的各类边界条件，采用均方误差函数mse计算；在步骤四中得到的复原流场上，使用步骤二中建立的卷积核差分算子，计算各个流场点的控制方程误差，控制方程包括navier-stokes方程、能量方程、连续方程；针对湍流情况，需要加入湍流模型，计算方程误差采用l2范数误差。
21.本发明的进一步技术方案是：所述边界条件误差包括第一边界条件误差、第二边界条件误差、第三边界条件误差。
22.本发明的进一步技术方案是：所述步骤六中，基于步骤五中得到的损失函数值，对步骤三中建立的卷积神经网络进行训练，直至收敛，得到最终模型。
23.本发明的进一步技术方案是：所述步骤六中，训练算法包括l-bfgs算法、adam算法、rmsprop算法。
24.有益效果
25.本发明的有益效果在于：应用本发明的结合卷积神经网络和卷积差分格式的流场计算方法，通过设计卷积神经网络结构和卷积核差分算子，基于各个流场点的目标参数值，计算各阶微分项，可以解决内嵌物理知识神经网络在求解流场时，由于计算微分项采用自动微分技术造成的不稳定性问题；通过自主设计神经网络的边界条件损失函数和控制方程损失函数，实现对该流场计算问题的各类约束，避免利用商用cfd软件，不能灵活进行求解设计的问题。
附图说明
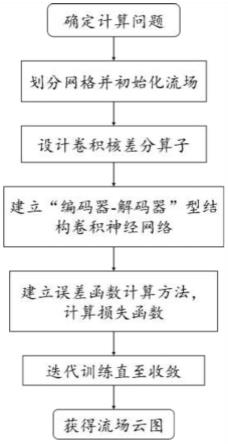
26.图1是根据本发明实施例可选的一种流场计算流程示意图；
27.图2是根据本发明实施例可选的一种翼型流场计算过程示意图；
28.图3是根据本发明实施例可选的一种叶栅流场计算结果水平方向速度分布图；
29.图4是根据本发明实施例可选的一种叶栅流场计算结果竖直方向速度分布图。
具体实施方式
30.下面通过参考附图描述的实施例是示例性的，旨在用于解释本发明，而不能理解为对本发明的限制。
31.参见图1-图2，将划分好的流体计算网格域以二维图像形式输入给卷积神经网络，经过编码器(encoder)和解码器(decoder)得到相同大小的二维流场分布，在该输出流场上对其进行卷积差分离散，得到速度的一阶微分、速度的二阶微分、压力的一阶微分，代入计算偏微分方程的误差；在输出流场上将边界点处的参数值与边界条件对比，计算边界条件的误差。
32.计算得到两部分误差以后，将两部分误差加权求和，反馈给卷积神经网络，通过训练算法，实现卷积神经网络中的参数更新。参数更新以后的卷积神经网络，可以产生新的流场图像，那么再次按照上述步骤计算得到新的误差，再次更新卷积神经网络，重复以上步骤直至达到收敛条件。
33.卷积神经网络停止训练后，再将需要计算的流场图像输入给卷积神经网络，即可获得精度满足要求的流场分布。
34.本发明方案的具体实施例包含以下步骤。
35.步骤一，确定流体物性参数以及边界条件。需要确定流体的物性参数以及边界条件，包括但不限于：流体密度、流体粘性系数、流体初始压力、流体初始温度、流体初始速度分布、流体初始压力分布、固体换热边界条件、速度边界条件等。
36.步骤二，建立卷积核差分算子并划分流体域网格。对于一阶微分项，采用一维卷积算子进行差分计算，对于拉普拉斯算子，采用二维卷积算子进行差分计算，基于步骤一中的边界条件，选用合适的差分类型，针对不同差分类型设置不同大小的卷积核；流体域的划分需要与卷积核差分算子相匹配，对于规则流体域，采用直角坐标系直接划分流体域，对于不规则流体域，采用贴体坐标系划分网格。
37.步骤三，建立卷积神经网络。卷积神经网络采用“编码器-解码器(encoder-decoder)”框架，包括但不限于“u型卷积神经网络(u-net)”结构和“全卷积神经网络(fcn)”结构。神经网络的层数和各层节点数对最终流场结果的准确性影响较大，神经网络的深度和各层节点数由步骤二中划分的计算流体域网格数直接决定，两者近似成正比关系，对于一个64
×
64的流体域，需要2层编码器(encoder)和2层解码器(decoder)，每层64个节点；网格数增加，需要增加神经网络层数和各层节点数，应该保持编码器(encoder)部分卷积网络层数和解码器(decoder)部分反卷积网络层数一致。
38.步骤四，初始化流场参数。初始化流场速度、压力、密度、温度目标参数，形成流场云图，将流场云图输入给步骤三中的卷积神经网络，经过编码器(encoder)提取高维特征，再经过解码器(decoder)复原到流场云图。
39.步骤五，计算神经网络损失函数值。神经网络的误差函数值由两部分加权组成，边界条件误差和控制方程误差。边界条件误差采用均方误差函数(mse)计算，依据步骤一中的具体边界条件，可以包括第一边界条件误差、第二边界条件误差、第三边界条件误差。例如边界条件中给定了无滑移边界，则需要将神经网络输出流场云图中，壁面边界处的速度值与0作差，计算得到这一边界条件的误差，其他边界条件的误差计算类似。在步骤四中得到的复原流场上，使用步骤二中的卷积差分算子，计算各个流场点的控制方程误差，计算方程误差采用l2范数误差，控制方程包括navier-stokes方程、能量方程、连续方程，针对湍流情况，需要加入湍流模型。例如计算二维流体域中各点关于定常navier-stokes方程的误差，可以采用如下公式：
[0040][0041]
步骤六，训练神经网络。基于步骤五中得到的损失函数值，训练步骤三中建立的卷积神经网络。首先，选用一种合适的训练算法，训练算法包括但不限于l-bfgs算法、adam算法、rmsprop算法等。当采用l-bfgs算法时，需要设置其学习率，学习率的设置对最后的流场结果影响较大，一般在计算雷诺数为100时，学习率设置为0.15，在雷诺数为1000时，设置为0.015，再增大雷诺数，学习率应该减小，最小在0.001左右。而采用adam算法和rmsprop算法，设置默认学习率即可，即0.001。
[0042]
步骤七，重复步骤四、步骤五、步骤六，直至最终误差达到收敛标准，停止训练。收敛标准一般设置为误差限制，即当迭代误差小于某一个数值时，停止训练。这个误差限制，根据具体问题的精度要求进行设置。特别地，为了改进训练效果，可以在每次训练时，将卷积神经网络的输入流场图设置为上一次训练的输出流场图，加快卷积神经网络的收敛，最终可以获得训练完成的模型。
[0043]
步骤八，计算流场云图。将需要计算的流场图输入给步骤七中得到的训练完成的模型，得到的输出云图即为所求流场结果。这里需要计算的流场图分两种情况，如果训练时，每次输入给卷积神经网络的流场图是训练开始初始化的流场图，那么需要计算的流场图就是该初始化的流场图；如果训练时，每次输入给卷积神经网络的流场图是上一次的输出流场图，那么需要计算的流场图就是最后一次训练的输出流场图。
[0044]
尽管上面已经示出和描述了本发明的实施例，可以理解的是，上述实施例是示例性的，不能理解为对本发明的限制，本领域的普通技术人员在不脱离本发明的原理和宗旨的情况下在本发明的范围内可以对上述实施例进行变化、修改、替换和变型。