一种乘加性模型的水平集图像分割方法

本发明属于图像处理领域，涉及一种乘加性模型的水平集图像分割方法。

背景技术：

1、对于实际中大量存在的自然图像、医学图像、工业图像等数字图像，由于光照的不均匀变化，以及成像设备的非理想性及缺陷，容易造成图像的降质和退化，从而出现灰度不均匀现象，这为图像处理和计算机视觉带来诸多难题。由于图像的灰度在一定区域内相互重叠，使得灰度不均匀图像的分割变得极为困难。

2、图像分割是数字图像处理的主要研究内容，在目标分割和轮廓提取的基础上，才能实现目标识别、几何测量等后续操作。实际数字图像通常包含噪声和各种非理想因素，灰度分布不均匀和局部对比度偏低等负面现象比较常见，而传统分割算法所能达到的精度较低，甚至可能出现错误分割的情况。基于阈值的分割方法通过选择合适的阈值将图像划分为二值图像，计算简单，适应性强，但该方法对噪声和灰度不均匀性敏感。基于区域的算法相对简单，对噪声的免疫力较强，但计算效率低，且依赖于特定的增长、分裂与合并法，适应性较差。基于神经网络的分割可以在数据偏离正常情况时实现分割，但该方法对数据集的构建和训练要求较高，效率较低下。近些年来，结合特定理论的分割算法逐渐兴起，而水平集分割技术以偏微分方程理论为基础对噪声不敏感，能够获得亚像素(亚体素)级光滑封闭的轮廓曲线，结合先验知识可以较好地克服图像的灰度不均匀性，在图像分割领域中具有优势。

3、一些基于区域的水平集模型假设图像是由灰度分布均匀的分片常数图像组成，所以无法分割灰度不均匀的图像。为了处理灰度不均匀图像，研究者提出了多种基于水平集理论的图像分割方法。区域尺度拟合模型在零水平集轮廓内外侧构造了两个局部逼近轮廓的灰度拟合函数，并在拟合项中嵌入核函数以指导轮廓的运动，从而实现对灰度不均匀图像的分割，但当核函数中心远离零水平集时，该模型无法定义前景和背景的拟合函数值，往往造成分割失败。局部灰度聚类水平集分割方法将乘性图像模型与水平集方法结合，根据图像灰度聚类准则得到表征图像灰度的水平集能量泛函，实现灰度不均匀图像的分割，但乘性模型无法充分表征图像的灰度不均匀性质，在分割具有严重灰度不均匀图像时容易失败，此外该方法也无法处理三维图像数据。针对三维图像数据的分割应用，3d鲁棒chan-vese模型引入了图像局部区域的灰度信息，提出一种解决含噪声ct体数据的分割方法，但该模型假设三维图像数据的灰度分布是均匀的，因此无法分割灰度不均匀的三维图像。本发明针对上述诸多问题，提出一种乘加性模型的水平集图像分割方法，用乘加性模型表征图像的灰度不均匀性，并将其与水平集方法相结合，以有效解决灰度不均匀及噪声图像的分割难题。

技术实现思路

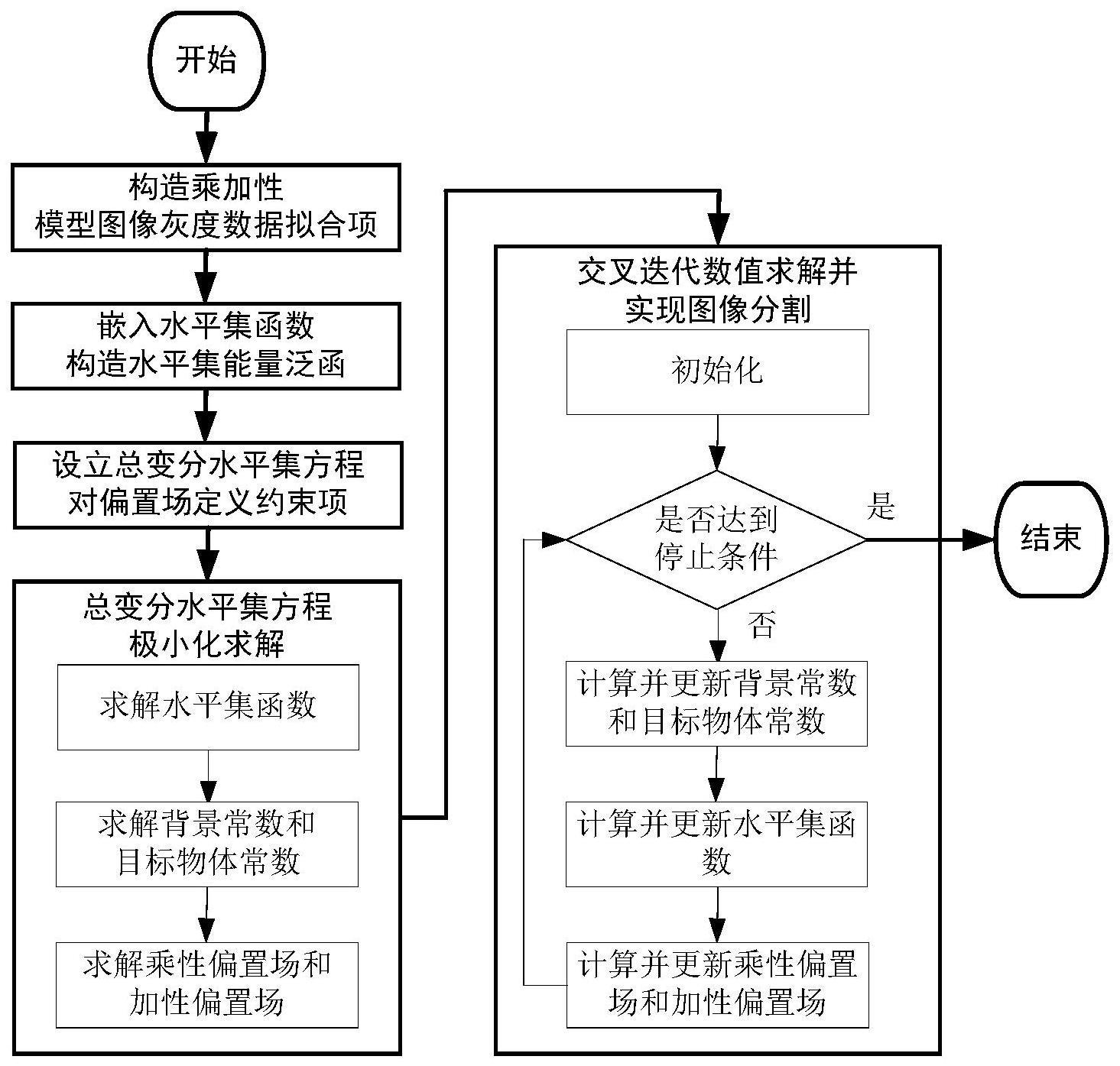
1、针对图像降质和灰度不均匀导致的图像分割不准确、不完整问题，本发明提供一种乘加性模型的水平集分割方法，用乘性偏置场和加性偏置场表征图像的灰度不均匀性质，并通过构造图像灰度数据拟合项、嵌入水平集能量泛函、定义偏置场约束项、设立总变分水平集方程、获取各迭代项并交叉迭代数值求解，实现图像分割。该方法可同时适用于二维和三维图像数据的分割。

2、本发明解决其技术问题所采取的技术方案包括以下步骤：

3、步骤1：将乘加性模型定义为i＝b1j+b2+n，其中i是观测图像，b1和b2分别是灰度不均匀乘性偏置场、加性偏置场，j是真实图像，n是加性噪声，该模型用两个不同性质的偏置场表示图像的灰度不均匀性质，并根据该模型构造图像灰度数据拟合项，当处理二维图像数据时采取下述方法进行：

4、(1)设真实图像j在不相交的区域ω1,…,ωn分别取n个不同常数值c1,…,cn；

5、(2)设定常数c1,…,cn为向量c＝(c1,…,cn)，将乘加性模型改写为i(x)≈b1(y)ci+b2(y)+n(x)，其中x和y分别为观测图像和偏置场中的像素灰度，对二维图像中的像素，考虑以其为中心半径为ρ的圆形邻域，并根据图像邻域内灰度的聚类属性制定二维图像数据的拟合项：

6、

7、式中k(s)为高斯截断函数，计算公式为：

8、

9、其中a是归一化常数，σ是高斯函数的标准差。

10、步骤2：在上述数据拟合项中嵌入符号相反的两个水平集函数，以指导轮廓曲线运动，并构造水平集能量泛函，当处理二维图像数据时采用下述方法进行：

11、(1)设定为水平集函数，用符号相反的水平集函数定义两个不相交的区域ω1＝{x:φ(x)>0}和ω2＝{x:φ(x)<0}，设定ω1和ω2分别由成员函数m1(φ)＝h(φ)和m2(φ)＝1-h(φ)表示，此处h是heaviside函数，定义为：

12、

13、其中ζ取1，h(x)的导数δ(x)定义为：

14、

15、(2)在式(1)中引入水平集函数并交换积分顺序，水平集能量泛函的计算公式为：

16、

17、(3)设定φ、c、b1和b2都是ε的变量，将ε改写为其中ei设定为：

18、ei(x)＝∫k(y-x)|i(x)-b1(y)ci-b2(y)|2dy (6)，

19、ei采用下式计算：

20、

21、式中*是卷积运算符，1k＝∫k(y-x)dy，该函数在除靠近ω的边界处其余都等于常数1。

22、步骤3：设立总变分水平集方程，将上述水平集能量泛函嵌入其中，并分别对乘性偏置场和加性偏置场定义约束项，当处理二维图像数据时采用下述方法进行：

23、(1)设定水平集函数长度正则项和距离正则项分别为具体定义如下：

24、

25、

26、其中计算零水平集轮廓的弧长以保证轮廓曲线的光滑性，的作用是保持水平集函数在演化中的稳定，其中

27、(2)设定在目标物体外部对b1进行约束的约束项其作用是保持b1在目标物体外部约等于常数1，具体定义如下：

28、

29、(3)设定在目标物体外部对b2进行约束的约束项其作用是让加性偏置场b2在背景处等于观测图像i，具体定义如下：

30、

31、(4)设立总变分水平集方程为：

32、

33、其中ν、μ、λ1、λ2为权重系数。

34、步骤4：分别固定各个变量，采用梯度下降法对总变分水平集方程进行极小化求解，得到各迭代项，当处理二维图像数据时采用下述方法进行：

35、(1)固定式(12)中的c、b1和b2，使用梯度下降法得到φ的极小化求解方程：

36、

37、其中div(·)是散度符号，函数dp定义为

38、(2)固定φ、b1和b2，使用梯度下降法得到最佳常数估计值和

39、

40、

41、此处ui(y)＝mi(φ(y))；

42、(3)固定φ和c，使用梯度下降法得到最佳偏置场估计值和

43、

44、

45、步骤5：利用有限差分法及递增序列的延续策略对各迭代项进行交叉迭代数值求解，实现图像分割，当处理二维图像数据时采用下述方法进行：

46、(1)使用有限差分法对式(13)进行数值离散，计算公式为：

47、

48、其中△t是时间步长，m是迭代次数；

49、(2)采用交叉迭代方法和递增序列的延续策略对各变量进行数值求解，实现图像分割，具体步骤如下：

50、1)初始化φ、b1和b2，设定λ2max；

51、2)计算λ2，当λ2<λ2max时继续执行下一步，否则退出循环，所得最新的φ就是二维图像数据的分割结果；

52、3)根据式(14)、式(15)计算并更新和

53、4)根据式(18)计算并更新φ；

54、5)根据式(16)、式(17)计算并更新和

55、6)返回步骤2)。

56、上面所述的一种乘加性模型水平集图像分割方法，主要以处理二维图像数据进行了技术方案描述。需要特别说明的是，上述方法可以拓展应用于三维图像数据分割，当处理三维图像数据时将上述方法中涉及的二维对象替换或拓展为三维对象，为保持方法描述的一致性对三维对象不另取符号标注，具体采用下述方法进行：

57、(1)乘加性模型仍然表示为i(x)≈b1(y)ci+b2(y)+n(x)，其中x和y分别为三维观测图像和三维偏置场中的像素灰度，对三维图像中的像素，考虑以其为中心半径为ρ的球形邻域，根据图像邻域内灰度的聚类属性，制定三维图像数据的拟合项为：

58、

59、(2)在三维图像数据的拟合项中嵌入符号相反的两个水平集函数，同时施加水平集函数长度正则项和距离正则项，另外考虑三维图像数据的信息更加充分和可靠，对偏置场不再设置约束，从而组成总变分水平集方程为：

60、

61、(3)利用梯度下降法对总变分水平集方程的各个变量进行极小化求解，计算公式为：

62、

63、

64、

65、

66、

67、(4)使用有限差分法对式(21)进行求解，计算公式为：

68、

69、(5)使用交叉迭代法对各变量进行数值求解，实现三维图像数据分割，具体步骤如下：

70、1)初始化φ、b1和b2，设定最大迭代次数mmax；

71、2)当迭代次数m<mmax时继续执行下一步，否则退出循环，所得最新的φ就是三维图像数据的分割结果；

72、3)根据式(22)、式(23)计算并更新和

73、4)根据式(26)计算并更新φ；

74、5)根据式(24)、式(25)计算并更新和

75、6)迭代次数m+1，返回步骤2)。

76、本发明的有益效果是：本发明提供的乘加性模型相比其他图像模型能更准确地表征图像的物理特性，而且分别对乘性偏置场和加性偏置场施加合理约束可以保证分割算法的稳定性，对灰度不均匀图像分割能更完整地提取出目标轮廓，在自然图像、医学图像和工业图像的分割应用中具有突出的准确性、可靠性和通用性。此外，当把乘加性模型水平集分割方法应用于三维图像数据时，可以有效利用相邻图像之间的连续性，增强对图像噪声和灰度不均匀的鲁棒性，提高三维图像数据的分割精度和可靠性。

77、下面结合附图和实施例对本发明做进一步说明。