一种基于人工神经网络的风速预报订正方法

1.本发明属于人工智能领域，涉及一种基于人工神经网络的风速预报订正方法。


背景技术：

2.随着传统能源消耗的加剧，清洁可再生能源的研究和开发越发紧迫和重要。其中风能绿色环保可再生，吸引越来越多的国家投资建立风力发电厂。而风速是影响风力发电持续稳定的关键因素，这就对风速预报提出了更高的要求。
3.近几十年来，随着数值天气预报(nwp)的飞速发展，风速预报的过程由传统的预报员分析天气图进行主观预报转变为主观与客观相结合的模式，即“经验预报+nwp结果”模式。虽然数值天气预报(nwp)是客观的定量计算，但其计算是基于网络格点进行的，代表的意义是一个矩形区域内天气要素的平均值，而不能针对一个气象台所在的观测站点直接做出要素预报，这就需要预报员“从格点到站点”进行人工经验订正。当遇到复杂天气形势时，预报员还要通过多人会商的方式来确定最终的天气要素预报结果，因此不可避免地在很大程度上带有主观性，引入不易量化的人为误差。
4.目前适合用于风速预报订正的方法有很多，广泛应用的方法可分为两大类：物理模型和统计模型。其中数值天气预报(nwp)系统是一个常用的物理模型，用于天气预报以及风速预报，然而这个物理模型是基于庞大、复杂且具有实验性的气象系统，需要大量气象信息和物理机制，这使得其应用和建模变得复杂。统计模型需要风速和时间戳等历史数据来进行预测，各种统计学习算法也应用于风速预报行业，例如整合移动平均自回归模型(arima)模型、人工神经网络(ann)等，此外还有一些混合方法。然而这些基于统计模型的风速预报，在短期预测中可以实现良好的精度，但由于误差累积问题，在长期预测中具有较差的性能。nwp等物理模型虽然可以实现大时间尺度预测，但预测结果粗糙且精度低。


技术实现要素：

5.有鉴于此，本发明的目的在于提供一种基于人工神经网络的风速预报订正方法。该方法使用历史数值天气预报结果和实况观测值，训练出一个人工神经网络模型，再将该模型应用于每日实时发布的数值天气预报结果中，得到台站级别的风速预报订正结果，达到更好地利用现有的预报产品，继承过往预报经验，并彻底排除人为主观干预带来的不确定性。该模型能够实现最大限度地减少预测误差，在风速预报中提供一种高精度、纯客观、实时风速预报后处理方法。
6.为达到上述目的，本发明提供如下技术方案：
7.一种基于人工神经网络的风速预报订正方法，包括以下步骤：
8.s1：整理目标区域内10米风场历史预报格点数据和对应的实况数据，并进行数据预处理；
9.s2：使用聚类算法对数据进行聚类分析，生成类别特征；
10.s3：采用时间序列预测方法对10米风场数据进行数据特点分析，生成特征向量，再
将步骤s2产生的类别特征，以及样本的预报时效添加到特征向量中，采用滑动窗口方法，对历史数据进行处理生成序列样本；
11.s4：设计与训练基于lstm的风速预报订正模型；
12.s5：使用训练后的基于lstm的风速预报订正模型对风速预报进行订正。
13.进一步，步骤s1中，对目标区域内包含10米风场数据的历史预报格点数据进行整理，并收集与之对应的格点实况数据，历史数据跨度为一年以上，包括每天utc 00:00和utc12:00起报的逐小时预报，预报时效为48小时，对整理的风场数据进行数据解析，然后通过mongodb数据库对解析和处理后的数据进行存储。
14.进一步，步骤s2中，对s1预处理后的数据使用k-means聚类算法进行聚类分析，生成类别特征，作为下一步使用的特征之一；特征包括统计特征和位置特征，所述统计特征是表示历史nwp风速误差和附加相关信息的一般特征，所述位置特征是由使用地理位置数据的k-means无监督学习算法聚类的组。
15.进一步，步骤s3中，生成包括ori_diff、max、min、mean、median、q_25、q_75、std共8个特征向量；生成的每个序列长度为30，特征数为8个，间隔12小时，跨度为15天，即每个样本的形状为30*8，每个样本对应的标签为该序列的下一个ori_diff。
16.进一步，步骤s3中，将风速预测过程定义为其中是预测的10米风速，f(.)是数值预报模型；当收集实际测量值时，预测误差e
t
为：
[0017][0018]
式中，为t时刻的nwp风速，v
t
是在时间t测量的10米风速；
[0019]
所述采用时间序列预测(tsp)方法对风场数据进行分析，具体包括：通过基于先前数据开发模型并将其应用于进行预测一段时间内的未来值，对历史误差进行学习和建模，以预测未来误差，预测误差后，通过添加预测误差来订正nwp风速，公式如下：
[0020][0021][0022]
其中是时间t的预测误差，是修正后的nwp风速。
[0023]
进一步，步骤s4中，训练以位置模式和预测周期作为输入特征的广义模型，具体包括：
[0024]
利用长短期记忆人工神经网络lstm对具有循环结构的时间序列数据进行建模，对输入特征之间的函数关系进行建模最近的过去到未来的目标变量，所述lstm中导入了一个单元状态c和三个gate，gate由一个sigmoid神经网络层和一个逐点乘法运算组成，input gate对当前输入x
t
和之前的输出h
t-1
进行加权：
[0025]it
＝σ(wi·
[h
t-1
,x
t
]+bi)
[0026]
其中wi和bi分别是input gate的权重矩阵和偏置向量，σ()是输出范围为(0，1)的sigmoid函数，当接近1时，倾向于选择单元状态中的所有信息，而当接近0时，倾向于丢弃输入信息；
[0027]
然后通过将信息选择与输入向量相乘：
[0028][0029]
其中wc和bc分别是输入层的权重矩阵和偏置向量；
[0030]
选择的信息表示为：
[0031][0032]
其中
⊙
是逐元素乘法，是当前输入和先前输出组合而成的输入信息，是将存储在单元状态中的输入层的选定信息；
[0033]
forget gate决定存储在单元状态中的信息的哪一部分应该被遗忘，如下式所示：
[0034][0035]
其中wf和bf分别是forget gate的权重矩阵和偏置向量；
[0036]
新的单元状态是：
[0037][0038]
output gate决定应该输出哪一部分信息，即
[0039]on
＝σ(wo·
[h
n-1
,xn]+bo),hn＝on⊙
tanh(cn)
[0040]
其中wo和bo分别是forget gate的权重矩阵和偏置向量。
[0041]
进一步，将(x0,x1,x2,
…
,x
29
)输入到lstm网络中，lstm网络给出对下一个数据的预测，即x
30
，从x
30
中提取出ori_diff变量，对下一次的预报数据进行订正。
[0042]
进一步，基于lstm的风速预报订正模型训练过程如下：
[0043]
将数据集划分为训练集和验证集；
[0044]
在训练集上，采用5折交叉验证方法得到最优的超参数配置，包括lstm单元个数、初始学习率和批量大小；
[0045]
采用随机梯度下降方法，对模型权重进行训练，设定最大训练代数；
[0046]
风速数据为连续变量，使用均方误差mse作为损失函数：
[0047][0048]
训练模型直至使损失函数最低，得到最优模型参数，训练完成。
[0049]
本发明的有益效果在于：与传统的风速订正模型相比，数值结果表明，深度学习算法具有更好的特征表示能力，可以提高预测精度。本发明还可以在满足预测精度的同时显著简化工作流程。并且这种方法是基于客观计算的，没有任何人为主观性的影响。探索这种后处理系统，将有助于风速预报领域从“主观与客观相结合”的预报模式向单纯客观预报模式转变。
[0050]
本发明的其他优点、目标和特征在某种程度上将在随后的说明书中进行阐述，并且在某种程度上，基于对下文的考察研究对本领域技术人员而言将是显而易见的，或者可以从本发明的实践中得到教导。本发明的目标和其他优点可以通过下面的说明书来实现和获得。
附图说明
[0051]
为了使本发明的目的、技术方案和优点更加清楚，下面将结合附图对本发明作优选的详细描述，其中：
[0052]
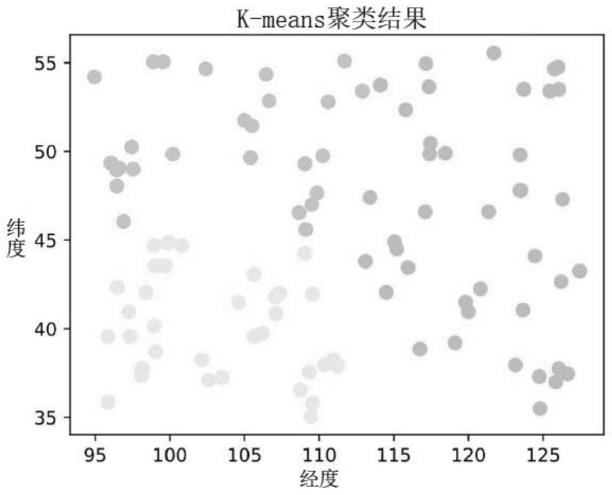
图1为gps位置聚类图；
[0053]
图2为某地的nwp预测误差热力图；
[0054]
图3为校正的时间序列预测图；
[0055]
图4为rnn模型结构图；
[0056]
图5为lstm神经元内部结构图；
[0057]
图6为lstm时间序列处理示意图；
[0058]
图7为人工神经网络模型训练曲线；
[0059]
图8为基于位置的总体rmse结果图；
[0060]
图9为基于预测周期的总体rmse结果图；
[0061]
图10为本发明所述基于人工神经网络的风速预报订正方法流程示意图；
[0062]
图11为本发明实施例的rmse热力图，其中(a)为订正前的热力图，(b)为订正后的热力图。
具体实施方式
[0063]
以下通过特定的具体实例说明本发明的实施方式，本领域技术人员可由本说明书所揭露的内容轻易地了解本发明的其他优点与功效。本发明还可以通过另外不同的具体实施方式加以实施或应用，本说明书中的各项细节也可以基于不同观点与应用，在没有背离本发明的精神下进行各种修饰或改变。需要说明的是，以下实施例中所提供的图示仅以示意方式说明本发明的基本构想，在不冲突的情况下，以下实施例及实施例中的特征可以相互组合。
[0064]
其中，附图仅用于示例性说明，表示的仅是示意图，而非实物图，不能理解为对本发明的限制；为了更好地说明本发明的实施例，附图某些部件会有省略、放大或缩小，并不代表实际产品的尺寸；对本领域技术人员来说，附图中某些公知结构及其说明可能省略是可以理解的。
[0065]
本发明实施例的附图中相同或相似的标号对应相同或相似的部件；在本发明的描述中，需要理解的是，若有术语“上”、“下”、“左”、“右”、“前”、“后”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此附图中描述位置关系的用语仅用于示例性说明，不能理解为对本发明的限制，对于本领域的普通技术人员而言，可以根据具体情况理解上述术语的具体含义。
[0066]
一种基于人工神经网络的风速预报订正方法，该方法包括以下步骤：
[0067]
s1：整理目标区域内10米风场历史预报格点数据和对应的实况数据，并进行数据预处理；
[0068]
s2：使用k-means等聚类算法对数据进行聚类分析，生成类别特征，作为下一步使用的特征之一；
[0069]
s3：采用时间序列预测(tsp)方法对10米风场数据进行数据特点分析，生成包括ori_diff、max等8个特征向量。再将s2产生的类别特征，以及该样本的预报时效添加到特征向量中，采用滑动窗口方法，对历史数据进行处理生成序列样本；
[0070]
s4：人工神经网络模型设计与训练；
[0071]
s5：对训练后的人工神经网络模型进行验证和评估。
[0072]
在所述步骤s1中，对目标区域内包含10米风场数据的历史预报格点数据进行整理，并收集与之对应的格点实况数据。历史数据跨度为一年以上，包括每天0时和12时(utc 00:00和utc 12:00)起报的逐小时预报，预报时效为48小时。对整理的数据进行数据解析，风场数据格式为hdf5，通过python中的pandas模块对存储hdf5进行解析和处理，然后通过mongodb数据库对解析和处理后的数据进行存储。
[0073]
选取目标区域内10米风场历史预报格点数据，以及对应的实况数据，如表1所示。
[0074]
表1
[0075]
列名含义备注10u_0预报10米风u分量订正因子10v_0预报10米风v分量订正因子win_1h_u-component of wind实况10米风u分量真实值标签win_1h_v-component of wind实况10米风v分量真实值标签
[0076]
在所述步骤s2中，对s1预处理后的数据使用k-means等聚类算法进行聚类分析，生成类别特征，作为下一步使用的特征之一。
[0077]
其中特征由特征工程创建，可分为两组：统计特征和位置特征。统计特征是表示历史nwp风速误差和附加相关信息的一般特征。位置特征是由使用地理位置数据的k-means无监督学习算法聚类的组。图1显示出了地理位置数据的聚类，其中位置被分类为3组。
[0078]
在所述步骤s3中，采用时间序列预测(tsp)方法对10米风场数据进行数据特点分析，生成包括ori_diff、max、min、mean、median、q_25、q_75、std共8个特征向量(见表2)。再将s2产生的类别特征，以及该样本的预报时效添加到特征向量中，采用滑动窗口方法，对历史数据进行处理生成序列样本。每个序列长度为30，特征数为8个，间隔12小时，跨度为15天，即每个样本的形状为30*8。每个样本对应的标签为该序列的下一个ori_diff。
[0079]
表2
[0080]
特征名含义ori_diff真实值与预报值的偏差max过去连续n个ori_diff的最大值min过去连续n个ori_diff的最小值mean过去连续n个ori_diff的平均值median过去连续n个ori_diff的中位数q_25过去连续n个ori_diff的第25％大的值q_75过去连续n个ori_diff的第75％大的值std过去连续n个ori_diff的标准差
[0081]
在所述步骤s4中，人工神经网络模型的设计中将风速预测过程定义为其中是预测的10米风速，f(.)是数值预报模型。数值预报模型包含错误，部分原因是由于驱动模型的数据质量和计算限制。有些错误是系统性的，需要通过应用统计后处理方法来减少。
[0082]
当前的数值预报(nwp)模型预测13-48小时内每12小时10米风速数据。此外，实际测量值每小时收集一次，因此预测误差e
t
可按如下公式计算。当收集实际测量值时
[0083]
[0084]
式中，为t时刻的nwp风速，v
t
是在时间t测量的10米风速。图2显示了一个位置的预测误差的热力图。
[0085]
有鉴于此，为了能够捕捉风速预测误差的变化规律，本发明采用时间序列预测(tsp)方法对风场数据进行分析。
[0086]
时间序列预测(tsp)方法通过基于先前数据开发模型并将其应用于进行预测一段时间内的未来值。按照tsp原理，对历史误差进行学习和建模，以预测未来误差，如图3所示。预测误差后，只需添加预测误差即可轻松订正nwp风速。这个过程由如下方程式表示：
[0087][0088][0089]
其中是时间t的预测误差，是修正后的nwp风速。
[0090]
但是基于tsp的算法仅利用历史错误信息，而其他特征如温度、气压等通常被忽略。此外，对于不同的位置和预测周期，基于tsp的算法需要单独建模，难度和工作量巨大。为了概括预测模型的应用场景，本发明选择使用深度学习算法——人工神经网络模型，因为它们能够自动学习从输入到输出的任意复杂映射，这在最近的时间序列预测任务中得到了广泛应用。
[0091]
基于深度学习的时间序列预测算法能够将位置模式和预测周期也考虑在内。因此可以训练以位置模式和预测周期作为输入特征的广义模型。
[0092]
其中循环神经网络(rnn)适用于对具有循环结构的时间序列数据进行建模，该结构使用神经网络对输入特征之间的函数关系进行建模最近的过去到未来的目标变量。图4显示了rnn的结构。
[0093]
从历史数据中学习到来自连续时隙的隐藏状态，具体来说，输出y
t
的预测不仅取决于输入的x
t
，而且还取决于隐藏状态的w
ht
，如等式4所示。w
ht
通过对先前输出y
t
进行加权，起到记忆先前信息的作用。然而，rnn具有由于每个时间步长的权重矩阵乘法而使梯度消失的缺点。因此rnn不善于捕捉长时间内出现的非平稳依赖关系。
[0094]yt
＝f(x
t
,w
ht
)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0095]
有鉴于此，考虑长短期记忆人工神经网络(lstm)是rnn的一种变体，可以克服rnn中梯度消失的问题。图5显示了lstm单元的结构，其中导入了一个单元状态c和三个gate，以实现长时间存储和访问信息。gate由一个sigmoid神经网络层和一个逐点乘法运算组成，它们能够选择性地让信息通过。首先，input gate对当前输入x
t
和之前的输出h
t-1
进行加权，如方程式5所示。
[0096]it
＝σ(wi·
[h
t-1
,x
t
]+bi)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5)
[0097]
其中wi和bi分别是input gate的权重矩阵和偏置向量，σ()是输出范围为(0，1)的sigmoid函数。当接近1时，倾向于选择单元状态中的所有信息，而当接近0时，倾向于丢弃输入信息。然后通过将信息选择与输入向量相乘。
[0098][0099]
其中wc和bc分别是输入层的权重矩阵和偏置向量。选择的信息表示为
[0100]
[0101]
其中
⊙
是逐元素乘法，是当前输入和先前输出组合而成的输入信息。是将存储在单元状态中的输入层的选定信息。
[0102]
forget gate决定存储在单元状态中的信息的哪一部分应该被遗忘，如下等式所示：
[0103][0104]
其中wf和bf分别是forget gate的权重矩阵和偏置向量。然后，新的单元状态是
[0105][0106]
output gate决定应该输出哪一部分信息，即
[0107]on
＝σ(wo·
[h
n-1
,xn]+bo),hn＝on⊙
tanh(cn)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(10)
[0108]
其中wo和bo分别是forget gate的权重矩阵和偏置向量。
[0109]
本发明中，将(x0,x1,x2,
…
,x
29
)输入到lstm网络中，lstm网络会给出对下一个数据的预测，即x
30
。我们从x
30
中提取出ori_diff变量，即可对下一次的预报数据进行订正，如图6所示。
[0110]
基于长短期记忆人工神经网络(lstm)的风速预报订正模型训练过程
[0111]
首先将数据集进行划分，训练集和验证集的比例为7：3。在训练集上，采用5折交叉验证方法得到最优的超参数配置，包括lstm单元个数、初始学习率和批量大小。最终确定初始单元个数为5，学习率为0.01，批量大小为32。采用随机梯度下降方法，对模型权重进行训练，最大训练代数为20。本模块通过python实现，分别对每个预报时效建立神经网络，进行训练。
[0112]
风速数据为连续变量，使用均方误差mse，
[0113][0114]
该损失函数适用于回归模型的训练，能够使模型较快地收敛。损失函数在16代左右达到最低点，保存为最优模型参数，训练曲线图(以13h为例)如图7所示。
[0115]
在所述步骤s5中，对训练后的长短期记忆人工神经网络(lstm)模型进行验证和评估。在本发明中，使用实际天气预报数据来验证所使用的人工神经网络订正模型的优越性，将原始数值预报风速误差与订正后的风速误差进行了比较。(以下实验是在一台linx pc上实现的，该pc配备amd ryzen 5 3550h、2.1ghz cpu、16gb ram和带tenserflow 2.8.0的python 3.8。)对于基于tsp的算法，训练数据是特定位置和特定预测周期的过去原始nwp风速误差。相反，对于基于深度学习的算法，所有位置和所有预测周期的过去原始nwp风速误差用于训练通用模型。
[0116]
基于位置的评估
[0117]
为了评估所提出的风速预报订正模型在所有位置上的订正和预测性能，使用均方根误差(rmse)作为性能标准。该值越小，意味着所提出模型的性能越好。
[0118][0119]
其中t∈n
t
为预测时隙，n∈nn为预测周期。因此rmse
loc
评估位置loc的整体预测性能。
[0120]
图8中评估了总体预测性能。箱线图用于比较基于位置的总体性能。数值预报曲
线，即左边的蓝色曲线，显示了未经订正的预测结果。rolling mean，ets，arima表示使用常规数据订正模型的nwp模型的预测结果，而lstm和cnn是使用深度学习算法订正的预测结果。从图8中可以看出，在不进行预测订正的情况下，最低rmse为1.1，而平均rmse几乎为2。基于tsp的算法和基于长短期记忆网络的预测订正算法都能够将预测误差降低到1.0。具体而言，rolling mean和lstm显示出最佳效果。
[0121]
综合比较，对预测结果进行订正是必要的，因为它可以显著提高预测精度。然而，如前所述，rolling mean，ets，arima方法都需要建立本地数值预报模型。这意味着如果位置发生变化，该模型将不再适用。人工神经网络模型不需要通过位置模式和预测周期数据重复训练，这使其更具有通用性。此外，图8显示出cnn算法与lstm算法相比降低了rmse的上限和下限，但lstm算法具有较低的平均rmse。在可靠性在天气预报方面具有最高优先级。因此，lstm仍然是最推荐的数值预报订正算法。
[0122]
基于预测周期的评估
[0123]
类似地，还计算了该风速预报订正模型在不同预测周期的rsme，来评估其订正和预测性能。
[0124][0125]
其中l∈n
l
是位置集。
[0126]
为了验证上述算法在短期风速预报中的应用，绘制了48小时内的预测结果，如图9所示。根据该图，未进行预测订正时，rmse为2.05。进行预测订正后，预测误差降低至1.7以下。请注意，cnn算法的rmse在前20小时内较高，然后降至1.7，并在随后的时间段保持稳定。基于长短期记忆网络(lstm)的风速预报订正模型的数值预报显示出优于其他算法的综合性能。
[0127]
综上所述，基于长短期记忆人工神经网络(lstm)的风速预报订正模型可以使整个风速预报订正过程响应及时，且风速预报订正效果出色。
[0128]
本实施例的流程图如图10所示，在训练完人工神经网络模型之后，在计算平台上运行，随机抽取10个格点的数据进行订正，抽取100个起报时刻为12时，预报时间为第13时的模式原始数据与后处理数据相对于实测数据的均方根误差热力图如图11所示，图11中(a)为订正前，(b)为订正后，图中颜色越深代表误差越大，模式预报数据的平均rmse约为2.0，订正后的rmse约为1.6。
[0129]
最后说明的是，以上实施例仅用以说明本发明的技术方案而非限制，尽管参照较佳实施例对本发明进行了详细说明，本领域的普通技术人员应当理解，可以对本发明的技术方案进行修改或者等同替换，而不脱离本技术方案的宗旨和范围，其均应涵盖在本发明的权利要求范围当中。